Abstract
Teachers often use open-ended questions to promote students’ deeper understanding of the content. These questions are particularly useful in K–12 mathematics education, as they provide richer insights into students’ problem-solving processes compared to closed-ended questions. However, they are also challenging to implement in educational technologies as significant time and effort are required to qualitatively evaluate the quality of students’ responses and provide timely feedback. In recent years, there has been growing interest in developing algorithms to automatically grade students’ open responses and generate feedback. Yet, few studies have focused on augmenting teachers’ perceptions and judgments when assessing students’ responses and crafting appropriate feedback. Even fewer have aimed to build empirically grounded frameworks and offer a shared language across different stakeholders. In this paper, we propose a taxonomy of feedback using data mining methods to analyze teacher-authored feedback from an online mathematics learning platform. By incorporating qualitative codes from both teachers and researchers, we take a methodological approach that accounts for the varying interpretations across coders. Through a synergy of diverse perspectives and data mining methods, our data-driven taxonomy reflects the complexity of feedback content as it appears in authentic settings. We discuss how this taxonomy can support more generalizable methods for providing pedagogically meaningful feedback at scale.Keywords
1. Introduction
The role of feedback on learning is well-established in educational research (Hattie and Timperley, 2007, Shute, 2008). Studies have shown that feedback can bridge the gap between a learner’s current understanding and the intended learning goals (Sadler, 1989, Kluger and DeNisi, 1996) and address any misconceptions that students may hold (Gusukuma et al., 2018). Feedback can foster other critical aspects of learning, including motivation (Narciss et al., 2014, Fong and Schallert, 2023) and self-regulation (Labuhn et al., 2010). Despite its importance, there remains a lack of consensus on which specific characteristics make feedback most effective across diverse educational contexts (Hattie and Timperley, 2007, Wisniewski et al., 2020). Some researchers suggest that feedback can foster deeper learning when its content highlights key concepts while minimizing cognitive load (Corral and Carpenter, 2020, Moreno, 2004). Others, however, place a larger focus on the timing of feedback (Kulik and Kulik, 1988, Abdu Saeed Mohammed and Abdullah Alharbi, 2022).
In many educational technologies, particularly in domains such as mathematics, correctness feedback can be provided immediately upon the submission of students’ responses due to the prevailing number of closed-ended problems, such as multiple-choice and fill-in-the-blank questions. Although correctness feedback can help identify areas where a student may be struggling, this alone is often insufficient to provide students with the types of guidance needed to remediate gaps in understanding. With growing interest in integrating self-explanation opportunities in digital learning platforms (Bisra et al., 2018, Rau et al., 2015, Wylie and Chi, 2014), prompting students to demonstrate not only procedural fluency but also their deeper conceptual reasoning behind their answers (e.g., Kwon et al. 2006, Munroe 2015), there is increased potential to explore more directed, elaborated, and exemplary forms of feedback.
Open-ended and explanation-focused questions can promote deeper learning, yet the time-intensive nature of interpreting students’ responses and crafting feedback makes real-time, high-quality intervention challenging to implement (e.g., Botelho et al. 2023). Recent advances in large language models (LLMs) (McNichols et al., 2024, Baral et al., 2024) present new opportunities, shifting the focus from how to generate feedback at scale to how to generate the most effective feedback to foster learning in specific contexts. However, evaluating the effectiveness of such feedback is complex due to the vastness of the pedagogical design space. For instance, personalized feedback messages are inherently tied to unique combinations of knowledge states, learner goals, and situational contexts, making it impractical to conduct traditional evaluation studies for every possible feedback instance across possible scenarios. Therefore, there is a need for a more generalized way of describing different types of feedback that is able to capture situational nuance without being so reductive that it obscures the personalized nature of the messages given. Such a framework would allow researchers and designers to compare, refine, and ultimately deliver targeted, personalized feedback across a wide range of contexts.
A foundational barrier to such scalability is the lack of empirically grounded frameworks that identify the types of feedback that teachers use in practice. Considering that theory-driven taxonomies may not capture the full range of instructional components or forms that feedback takes in authentic settings, prior work in educational technologies has often developed and applied coding schemes. While this inductive approach can more accurately reflect the structure of a given dataset, a lack of shared terminology results in inconsistencies in how feedback is interpreted, applied, and acted upon. For example, Boyer et al. (2008) categorized feedback into cognitive types (e.g., positive, lukewarm, negative, and neutral) and motivational types (e.g., praise and reassurance). A more recent study by Grawemeyer et al. (2017) expanded on this by treating the motivational component as a form of affective feedback and incorporated additional task-related categories, such as instructive and problem-solving feedback.
In this paper, we leverage several data mining methods to investigate the complexity of feedback content as it emerges from diverse interpretations. Specifically, we analyze teachers’ feedback messages in response to students’ open-ended work in an online middle school mathematics platform. Using a discovery-oriented modeling pipeline involving qualitative coding, factor analysis, and cluster analysis, we identify common structures and reconcile differing perspectives in the construction of a unified taxonomy. While initially informed by domain-specific features of mathematics instruction, our methodology provides a means of revealing broader patterns of feedback structure and intent as interpreted by both researchers and classroom teachers. Our broader goal is to support the design of feedback systems, whether human- or AI-driven, that require a structured understanding of feedback content that is grounded in authentic classroom practice. This work offers a foundational framework for organizing feedback at scale, enabling future research on the effectiveness of different types of feedback across various instructional contexts.
2. Related Work
2.1. Feedback Design in Educational Technology
Many digital learning platforms provide immediate correctness feedback and even textual feedback (e.g., Gurung et al. 2023) for closed-ended questions as exemplified by platforms such as McGraw Hill’s ALEKS, Carnegie Learning’s MATHia, and ASSISTments. As noted in the earlier section, correctness feedback offers a limited, but still important merit in various aspects (Aleven et al., 2016). For instance, the immediacy of feedback allows students to make timely adjustments to their conceptual understanding or learning strategies (Sweller, 2011, Mory, 2013, Vanacore et al., 2024). At the same time, teachers can use these systems to monitor progress, while researchers benefit from large-scale data without delays from human assessment, contributing to the rapid development of student models and better learning systems (e.g., Corbett and Anderson 1994, Baker et al. 2004, Baker et al. 2010).
While closed-ended questions are useful for assessing student learning and providing opportunities for practice, correctness feedback alone is often insufficient for facilitating deeper conceptual understanding when students struggle to learn new topics. Some platforms offer open-ended questions, which prompt students to articulate reasoning and problem-solving strategies (Chi, 2000, Chi et al., 1994). This format also brings teachers back into the feedback loop by surfacing students’ deeply rooted misconceptions or recurring patterns that may require targeted interventions. Research has shown that qualitative feedback written by teachers can enhance learning (Konold et al., 2004, Gan et al., 2021), particularly by fostering learner agency and critical thinking over time (Hargreaves, 2014). These are especially relevant in computer-based learning environments, where such targeted support is often limited yet critically needed (Van der Kleij et al., 2015).
Relatedly, a growing body of research has focused on automated scoring and generation of feedback across various domains, such as essay writing (Madnani et al., 2013, McNamara et al., 2015), computer science (Hou and Tsao, 2011, Klein et al., 2011), and science education (Lee et al., 2019). Researchers have also explored a variety of computational approaches, including machine learning (Hou and Tsao, 2011, Madnani et al., 2013), deep learning (Taghipour and Ng, 2016, Qi et al., 2019), and more recently, transformer- and LLM-based models (Gaddipati et al., 2020, Botelho et al., 2023, McNichols et al., 2024, Baral et al., 2024).
2.2. Opportunities and Challenges with Open Responses
Open-ended questions encourage students to articulate their mathematical problem-solving strategies and reasoning in their own words. In this self-explanation process (e.g., Rau et al. 2015, Wylie and Chi 2014), students are encouraged to demonstrate not only procedural fluency, but also the conceptual understanding underlying their answers (e.g., Bisra et al. 2018). These types of questions have long been of interest in K–12 mathematics education research (Anderson and Biddle, 1975, Boaler, 1998). Studies found that open-ended questions can reveal how students apply different strategies to solve a problem, offering insights into their thought processes that is not accessible through numeric answers in closed-ended questions (Chi et al., 1994, Bisra et al., 2018, Wylie and Chi, 2014). Moreover, open-ended questions have been identified as a promising approach for promoting learning transfer (Bahar and Maker, 2015), particularly in contexts where students must apply school-learned concepts and procedures beyond simply finding the correct answer in well-structured problems.
However, delivering pedagogically meaningful feedback at scale remains a major challenge. As the emphasis shifts from the correctness of the answer to the quality of the reasoning, teachers must interpret a wide range of responses, each reflecting varied approaches and levels of understanding. It is an effort that requires substantial expertise (Wylie and Chi, 2014), such as identifying misconceptions, evaluating the depth and logic of reasoning, and assessing both mathematical accuracy and fluency. In addition, designing feedback often requires multiple steps, such as aligning with learning goals, monitoring progress, and providing actionable next steps (Barabasheva, 2021). Traditionally, teachers invest considerable time and effort to deliver effective feedback that is tailored to students’ needs and contextualized within specific instructional settings (Shute, 2008).
Assessing open-ended responses presents unique challenges across disciplines, but this is particularly pronounced in mathematics, where student work is often concise and blends symbolic language, notations, and visuals (Baral et al., 2023). These practical difficulties are also reflected in the ASSISTments platform, where a decline in teachers’ use of open-ended questions has been observed over time (Baral et al., 2021, Erickson et al., 2020). Even when open-ended tasks are assigned, few are followed by teachers’ feedback or grading, suggesting that open-ended formats remain under-utilized despite their instructional value. Addressing these challenges requires advancing methodologies that better support teachers in interpreting and responding to open-ended student work.
2.3. Considerations for Operationalizing Teacher Feedback
To support teachers in scaling high-quality feedback, it is essential to understand how feedback functions in authentic classroom contexts and to identify certain types of feedback that are both pedagogically meaningful and potentially applicable more broadly (Kwon et al., 2006, Munroe, 2015). In research, two main approaches are commonly used to operationalize feedback: theory-driven taxonomies developed deductively from prior literature and coding schemes developed inductively from empirical data. While both approaches offer valuable insights, each is not without methodological limitations.
First, taxonomies can be developed deductively from theory-driven frameworks, which offer structured ways to conceptualize feedback based on established literature. For example, Hattie and Timperley (2007) described four feedback levels (i.e., task, process, self-regulation, and self) while Yang and Carless (2013) expanded the concept to include cognitive, social-affective, and structural dimensions, considering not only feedback content but also the broader feedback processes. More recently, Ryan et al. (2021) proposed a learner-centered framework that focuses on how effective feedback involves actionable components for students. While valuable, these frameworks may not fully capture the full complexity of feedback content and instructional strategies, which are often shaped by teachers’ different judgment, norms, and commitments (Meier et al., 2006, Thompson and Senk, 1998).
Second, data-driven approaches often develop coding schemes inductively, grounding them in the specific context of the study. This is particularly common in the design of agents that deliver real-time feedback in computer-based learning environments, where frameworks are derived from patterns in annotated corpus data. For example, Boyer et al. (2008) categorized feedback into cognitive types (e.g., positive, lukewarm, negative) and motivational types (e.g., praise, reassurance), while Grawemeyer et al. (2017) expanded the typology to include task-oriented strategies such as reflective prompts and think-aloud support. Similarly, Cheng et al. (2022) identified both domain-general suggestions and domain-specific comments on content and presentation in human-delivered feedback. Although these inductive approaches are grounded in empirical data, they often reduce multiple coder perspectives to a singular interpretive lens (Saldaña, 2021), which may obscure alternative conceptualizations of feedback. In many cases, codes are treated as mutually exclusive despite evidence that feedback often embodies overlapping instructional and affective functions (Cheng et al., 2022). A more critical limitation concerns the potential disconnect between researchers who develop frameworks and teachers who implement them. As Coburn and Turner (2012) noted, even carefully constructed coding schemes may fail to align with the interpretive stances or pedagogical goals of practitioners, limiting their applicability in real-world classrooms.
As such, there is a need for a taxonomy that provides a shared language and a consistent interpretive framework across feedback agents, including students, teachers, and technological systems. To address the limitations outlined above, such a taxonomy should be firmly grounded in empirical evidence, co-developed by both researchers and practitioners serving as coders, and guided by a methodological approach that accounts for variation in interpretation. A taxonomy constructed through a contextualized and systematic analysis of feedback can preserve the richness and nuance of teacher practice while offering a structure that is interpretable to those involved in the design and implementation of assessment tools. More broadly, a taxonomy developed with methodological consideration for replicability has the potential to inform a wider audience. By supporting more generalizable approaches to analyzing, evaluating, and generating feedback, the resulting taxonomy can contribute to a deeper understanding of how feedback mechanisms operate across diverse contexts and educational systems.
Our investigation is guided by three research questions:
- RQ1. How do perceptions and judgments of feedback characteristics vary among individuals with different backgrounds and experiences?
- RQ2. What underlying factors emerge across varying perceptions and judgments of the feedback characteristics?
- RQ3. What types of feedback emerge from the measured factors?
3. Methodology
3.1. Study Context
This study is situated in ASSISTments (Heffernan and Heffernan, 2014), a free, web-based learning platform for K-12 mathematics education. Combining traditional classroom teaching methods with online educational materials and interactive problem-solving activities, the ASSISTments platform is used by more than 20,000 teachers across the United States (Feng et al., 2023). The assignments often contain a combination of closed-ended and open-ended questions. While closed-ended questions are automatically assessed in ASSISTments, open-ended problems require teachers to manually review student responses and provide written (or textual) feedback.
Specifically, we collected data from QUICK-Comments, a teacher-augmentation tool designed to support teachers in assessing open-ended student responses within the ASSISTments platform (Botelho et al., 2023). As shown in Figure 1, this tool allows teachers to select from a repository of pre-authored comments, which has been tailored to address common student errors or misconceptions. By streamlining the feedback process without compromising quality, QUICK-Comments allows teachers to efficiently deliver personalized, timely feedback while supporting a dynamic and responsive learning experience for students.
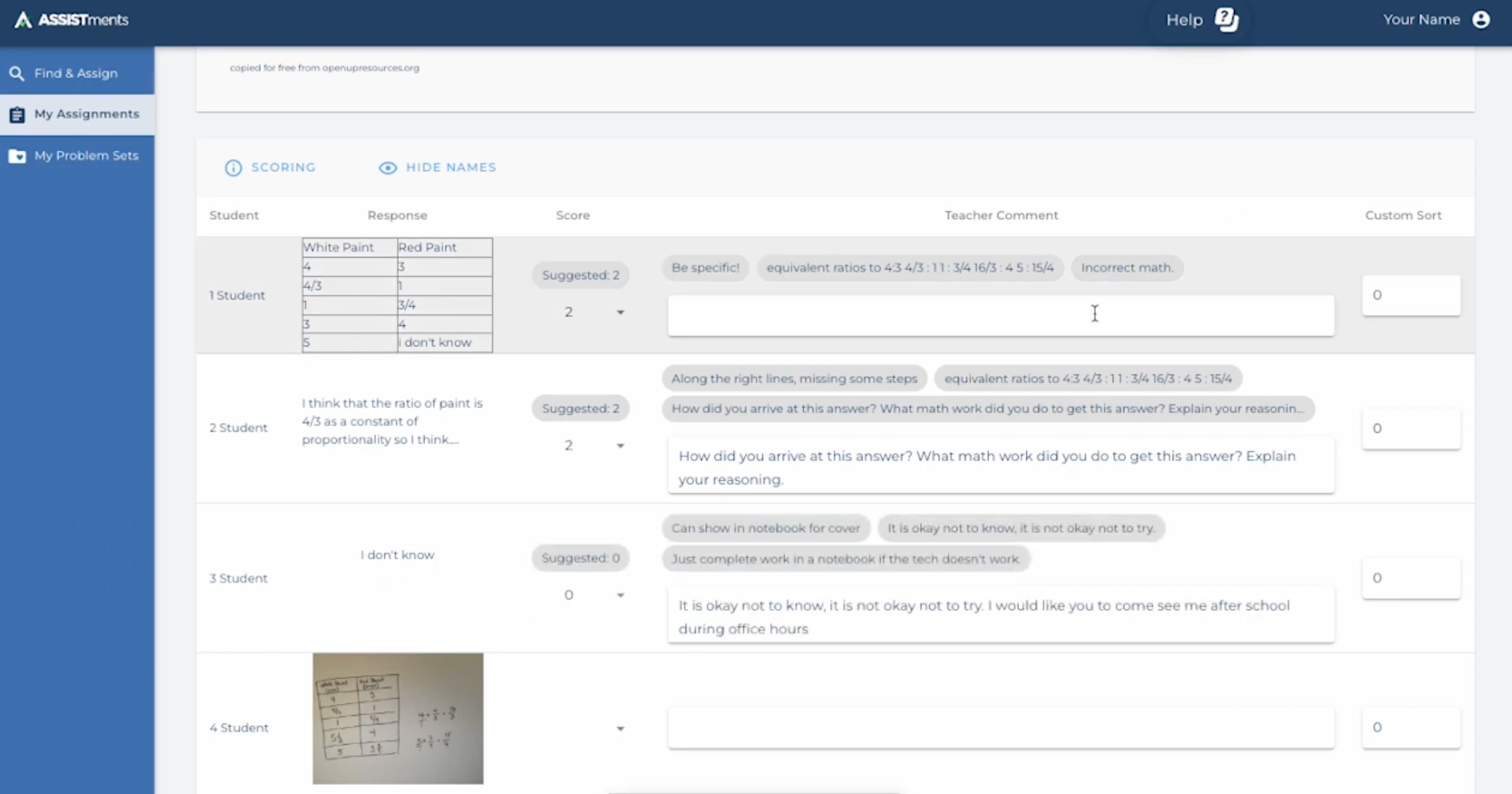
3.2. Dataset
The dataset1 we use in this study focuses on middle school mathematics and encompasses widely used open-response mathematics curricula. The dataset consists of 8,307 open-ended mathematics problems and 193,187 total responses from 23,853 different students. These open responses from the students were evaluated by their mathematics teachers, who assigned scores on a 5-point integer scale ranging from 0 to 4, with 0 being the lowest and 4 the highest. In addition to numeric scores, each student response was accompanied by teacher-authored textual feedback. A total of 1,296 teachers contributed to the full dataset.
For the present study, we randomly sampled 100 student responses and their associated feedback messages in two separate rounds. Both samples were used to iteratively develop and refine the coding scheme, and the second sample, once fully coded, served as the basis for the analysis reported in this paper. This analytic subset includes responses evaluated and annotated by 57 different teachers and drawn from 97 unique students, reflecting a wide range of performance levels. Approximately 14% of responses received a score of 0, 10% a score of 1, 25% a score of 2, 23% a score of 3, and 28% a score of 4.
3.3. Developing the Coding Scheme
| Feedback Characteristic | Description
|
|---|---|
| Personal | Individualized feedback that particularly calls upon a student’s name. |
| Confirmation | Acknowledges or affirms the correctness or accuracy of a student’s response to a question. |
| Generic | Broadly applicable feedback that is not specific to any particular mathematics topic or concept. |
| Specific | Addresses a particular mathematics topic, question, or details about a student’s mathematics work. |
| Positive Affect | Evokes positive emotions, attitudes, or feelings in the student with encouraging positive messages. |
| Negative Affect | Evokes negative emotions, attitudes, or feelings in the student with negative and discouraging messages. |
| Criticism | Offers a critical assessment of a student’s work, highlighting errors and shortcomings. These types of feedback are factual negative comments. |
| Emoji | Use of emoticons or graphical symbols, such as smiley faces in the feedback, to convey a teacher’s emotional state. |
| Explanation | Elaborate and informative explanations to help a student better understand a concept and solve a problem. |
| Question | Poses questions or follow-up inquiries to the student to encourage him or her to think critically or understand their processes better. |
| Correction | Identifies and rectifies errors in the student’s work, highlighting inaccuracies in the answer and offering guidance on correcting them. |
| Mathematical Suggestions | Recommendations or advice related to mathematical concepts, reasoning, or problem-solving strategies. |
| Learning Strategy Suggestion | Provides suggestions on how to improve the student’s learning approaches, study habits, and techniques. |
| Hints | Provides hints or subtle clues for the next steps without giving away the answer. |
| Example Response | Includes a sample or model response to a given question. |
| Follow-up | Teacher asks the student to follow up with them in person. |
| No Mathematics | Feedback which indicates the mathematics work is either missing or not shown. |
| Student Explanation | Feedback that asks for further clarification or explanation of the work. |
| Other | Any other feedback that doesn’t fall into the above-mentioned types. |
To understand and characterize different pedagogical dimensions exhibited through teacher-authored feedback messages, we developed a coding scheme through an iterative, expert-informed process. Three researchers from diverse cultural backgrounds in learning sciences and educational technology participated in the initial development of the codebook. One researcher drafted a preliminary set of codes, descriptions, and examples based on the sample dataset. Drawing from a previously developed feedback framework (Cheng et al., 2022), initial coding included positive and negative affect, criticism, question, correction, explanation, suggestion, and statement.
Two researchers independently applied this initial codebook to a sample of 100 teacher feedback messages. They then met to discuss disagreements and revise the codebook to incorporate additional types of feedback identified through coding. A second round of coding was conducted on another randomly sampled set of 100 feedback messages, followed by further reconciliation and refinement; Kappa scores were not calculated during these early iterations, with discussion around each sample instead taking place to confirm and understand reasoning behind both instances of agreement and disagreement. The researchers expanded the codebook by adding new codes and clarifying definitions to improve comprehensiveness.
3.4. Applying Coding Scheme
Following these iterations, a group of six expert coders was established to independently code a new random sample of 100 feedback messages using the updated codebook (see Table 1). This group included three researchers (two of whom were those who established the codebook) and three mathematics teachers with over 20 years of teaching experience, all of whom had some familiarity with the learning platform used in this study. Among the six coders, two researchers identified as Asian, while the remaining four (including the three teachers) identified as American.
In approaching the coding task, it is important to note that coders were encouraged to apply the codes based on how they interpret both the feedback messages and description of the feedback characteristics which form the codebook; their goal was to incorporate their individual perspectives in interpreting both the teacher-authored feedback as well as how each characteristic may be represented within each message.
Table 2 presents the Fleiss’ Kappa values for each feedback feature, computed separately for the research team, the teacher experts, and the combined group of all six coders. As described in our research questions, it is important to reiterate that the purpose of this calculation is not to validate the coding scheme, but to use this as an initial measure to identify differences in perspectives across coders. We expand on how the level of agreements also varied depending on the nature of the specific code in the subsequent section.
| Research Team | Teacher Experts | Combined | |
|---|---|---|---|
| Personal2 | — | -0.096 | — |
| Confirmation | 0.277 | 0.470 | 0.457 |
| Generic | 0.608 | 0.073 | 0.354 |
| Specific | 0.270 | 0.096 | 0.253 |
| Positive Affect | 0.888 | 0.644 | 0.748 |
| Negative Affect | -0.020 | 0.437 | 0.250 |
| Criticism | 0.537 | 0.385 | 0.405 |
| Emoji | 0.906 | 1.000 | 0.955 |
| Explanation | 0.521 | 0.548 | 0.527 |
| Question | 0.812 | 0.518 | 0.704 |
| Correction | 0.438 | 0.409 | 0.363 |
| Mathematical Suggestions | 0.411 | 0.262 | 0.337 |
| Learning Strategy Suggestion | 0.362 | 0.127 | 0.201 |
| Hints | 0.023 | 0.104 | 0.133 |
| Example Response | 0.176 | 0.472 | 0.312 |
| Follow-up | 0.240 | 0.427 | 0.418 |
| No Mathematics | 0.625 | 0.385 | 0.463 |
| Student Explanation | 0.213 | 0.363 | 0.259 |
| Other | 0.415 | 0.245 | 0.313 |
3.5. Correlation Analysis
Building on the qualitative coding, we conducted a correlation analysis to answer RQ1 (How do perceptions and judgments of feedback characteristics vary among individuals with different backgrounds and experiences?). Given that the data were not normally distributed, we used Spearman’s rank correlation as our analytical method (Hauke and Kossowski, 2011). We computed correlations within each group, first among the researchers, then among the teachers, and finally across all six coders combined. This comparative analysis enables us to examine how background factors such as disciplinary expertise and cultural experience may influence perceptions of feedback characteristics. Additionally, we analyzed the average of the ratings for each feature across coders, which serves as a middle-ground representation of consensus.
3.6. Factor Analysis
To address RQ2 (What underlying factors emerge across varying perceptions and judgments of the feedback characteristics?), we conducted an exploratory factor analysis (EFA) to uncover latent dimensions underlying the coded feedback characteristics. Of the original 114 variables derived from 19 feedback codes independently applied by six coders, six of them (i.e., “Personal” (N=4), “Negative” (N=1), and “Generic” (N=1)) contained null values throughout and were removed from this analysis, leaving 108 variables for analysis. In conducting our EFA, we intentionally made no prior assumptions about the relationships among the 114 variables that resulted from the 19 codes across the six coders. Instead, we treated each set of codes as uniquely distinct variables, thereby allowing the constructs to naturally emerge across different lenses of three researchers and three teachers. The number of factors was identified by using parallel analysis, which suggested a 12-factor solution. Based on this, we performed a Minimum Rank Factor Analysis (MRFA) with Promax rotation.3
3.7. Cluster Analysis
While the factor analysis revealed latent dimensions underlying teacher feedback, it remained unclear how these dimensions might form higher-order feedback types. To explore the higher-level structure of teacher feedback, we conducted a K-means clustering analysis using the factor scores from the previous analysis as input features. K-means is an unsupervised machine learning algorithm commonly used in exploratory analyses to identify underlying patterns in high-dimensional data. A key step in clustering is determining the optimal number of clusters (\(k\)). We used the silhouette method to evaluate multiple values of \(k\), selecting the number that yielded the highest average silhouette width. In parallel, we also manually explored a range of cluster sizes to ensure that the resulting clusters were interpretable and meaningfully distinct. From this, 10 clusters emerged from our analysis. To aid interpretation, we renamed the ten resulting clusters to reflect their defining feedback characteristics. The clusters are visualized in Figure 4 as a heatmap, where columns represent normalized factor scores (via z-scores), and rows represent cluster averages for each feature.
4. Result
The goal of this study was to construct a taxonomy of teacher feedback by using data mining methods to account for both the structural complexity of authentic data and the variability in coder perspectives. This section addresses each research question by focusing on how each stage contributed to a nuanced understanding and measurement of distinct feedback types.
4.1. Results of the Coding and Correlation
As shown in Table 2, while the research team generally showed higher agreement than the teacher experts, we found weak agreement with combined kappa values below 0.30 for certain codes, such as “Specific,” “Learning Strategy Suggestion,” and “Hints.” Also, we observed strong agreement among all coders for “Emoji” and “Positive Affect,” as these codes are operationalized in ways that make them more directly observable than others. Interestingly, teacher experts achieved stronger alignment within their group on a few features, such as “Negative Affect” and “Example Response,” suggesting that professional teaching experience may influence how certain types of feedback are perceived.
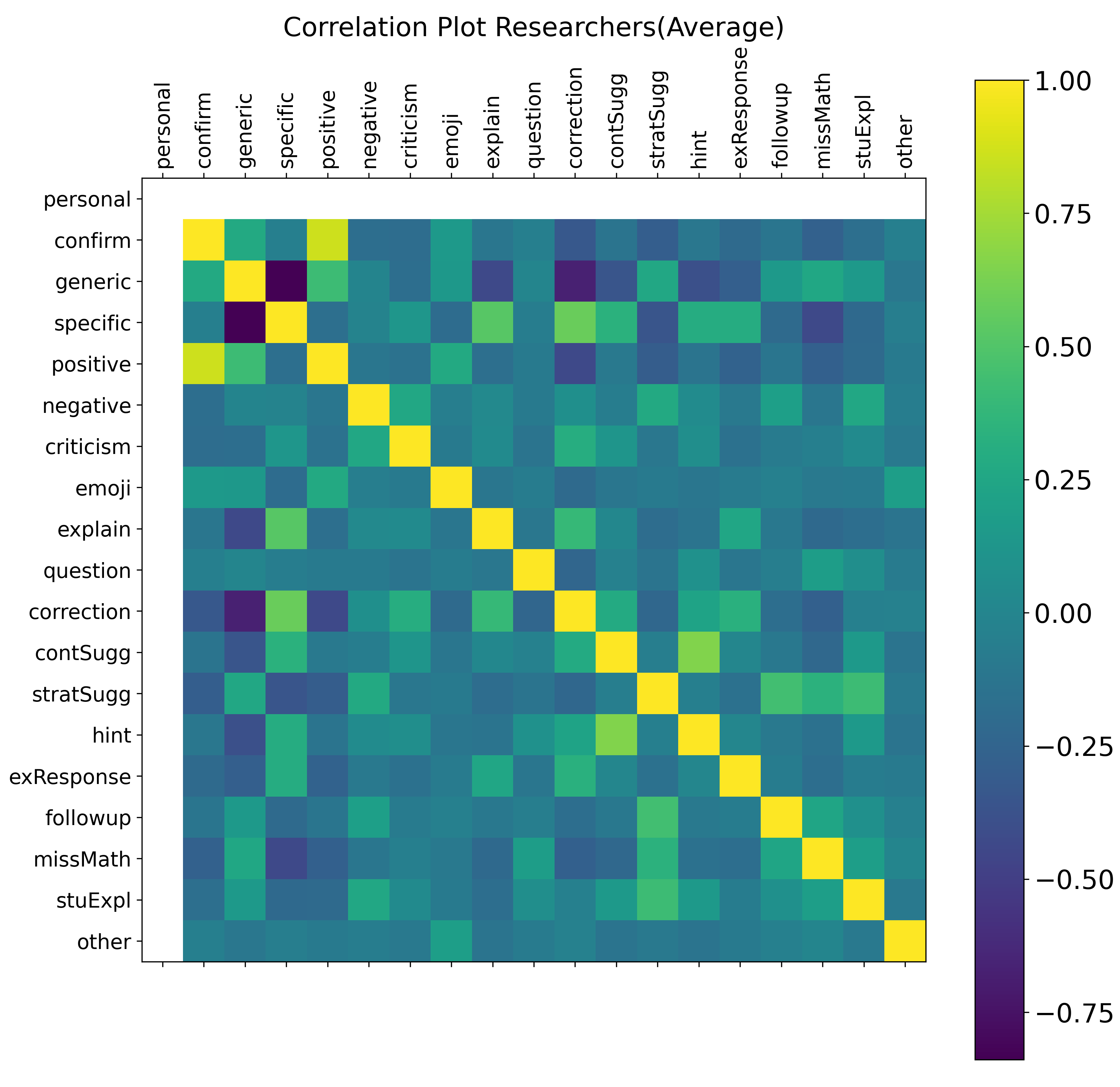
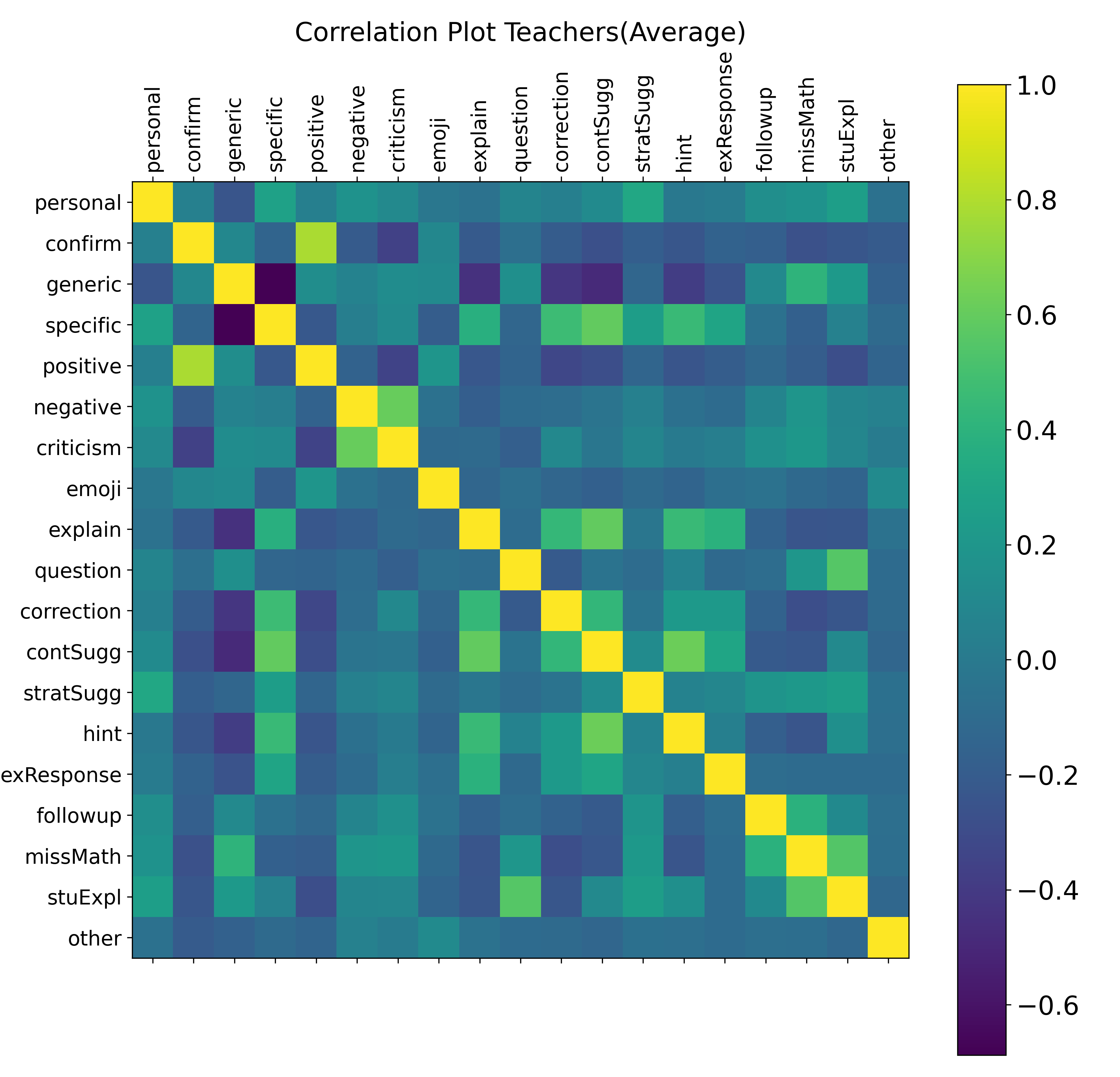
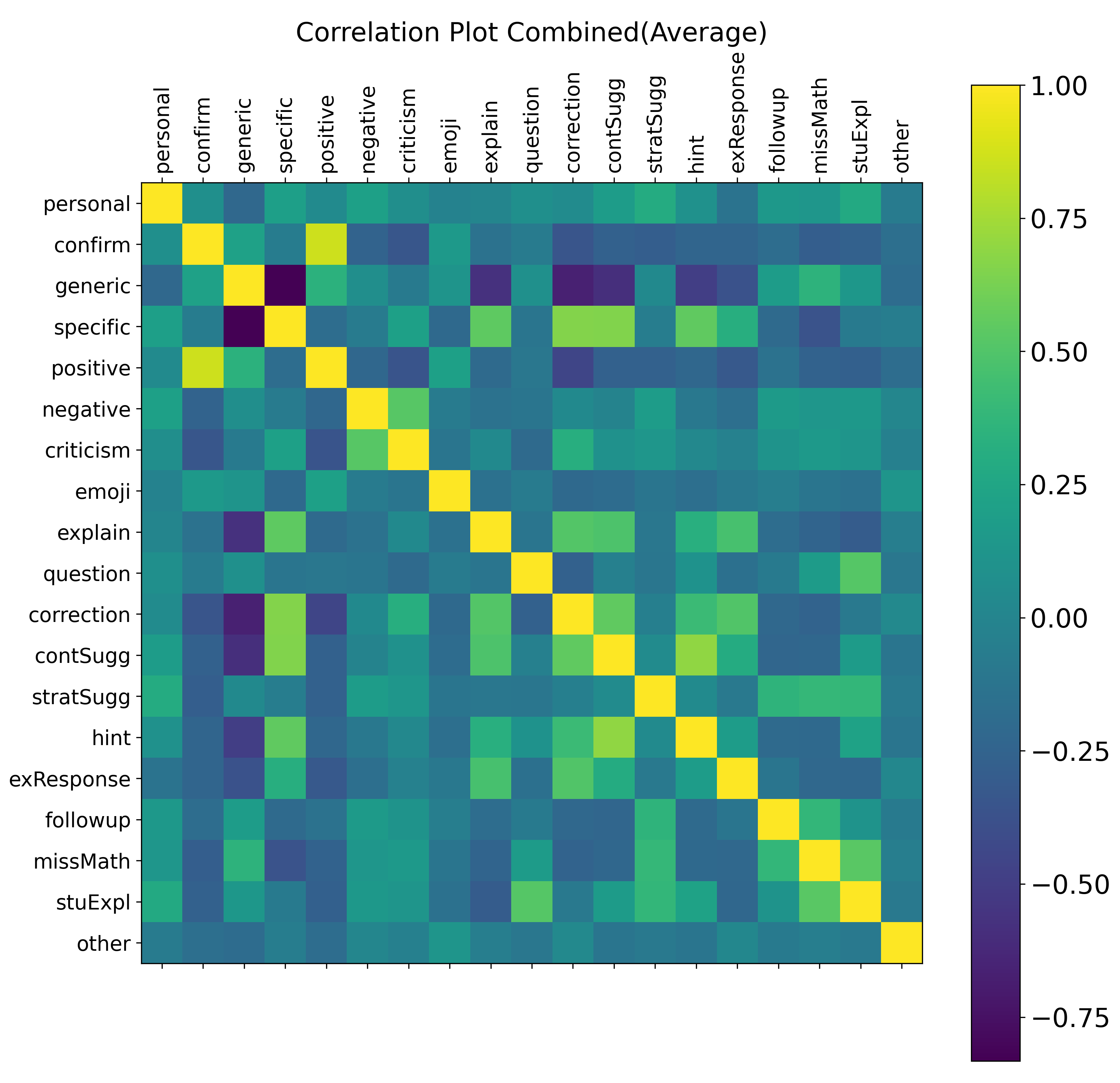
In the correlation analysis, we further examined similarities and differences between each coder group (i.e., researchers, teachers, combined) in the coding process. Figure 2 presents the pairwise correlations with stronger positive relationships visualized in bright green and yellow, and stronger negative associations in dark blue. For all coder groups combined, we observed strong positive correlations between several codes, suggesting that some codes commonly co-occur in practice. For instance, correlations between “Confirmation” and “Positive Affect,” suggest that when teachers affirm the correctness of a student’s response, such feedback is often perceived as emotionally supportive. Similarly, “Mathematical Suggestions” and “Hints” were positively correlated, indicating that teachers’ mathematical advice is often framed as scaffolds to support student understanding.
4.2. Results of the Factor Analysis
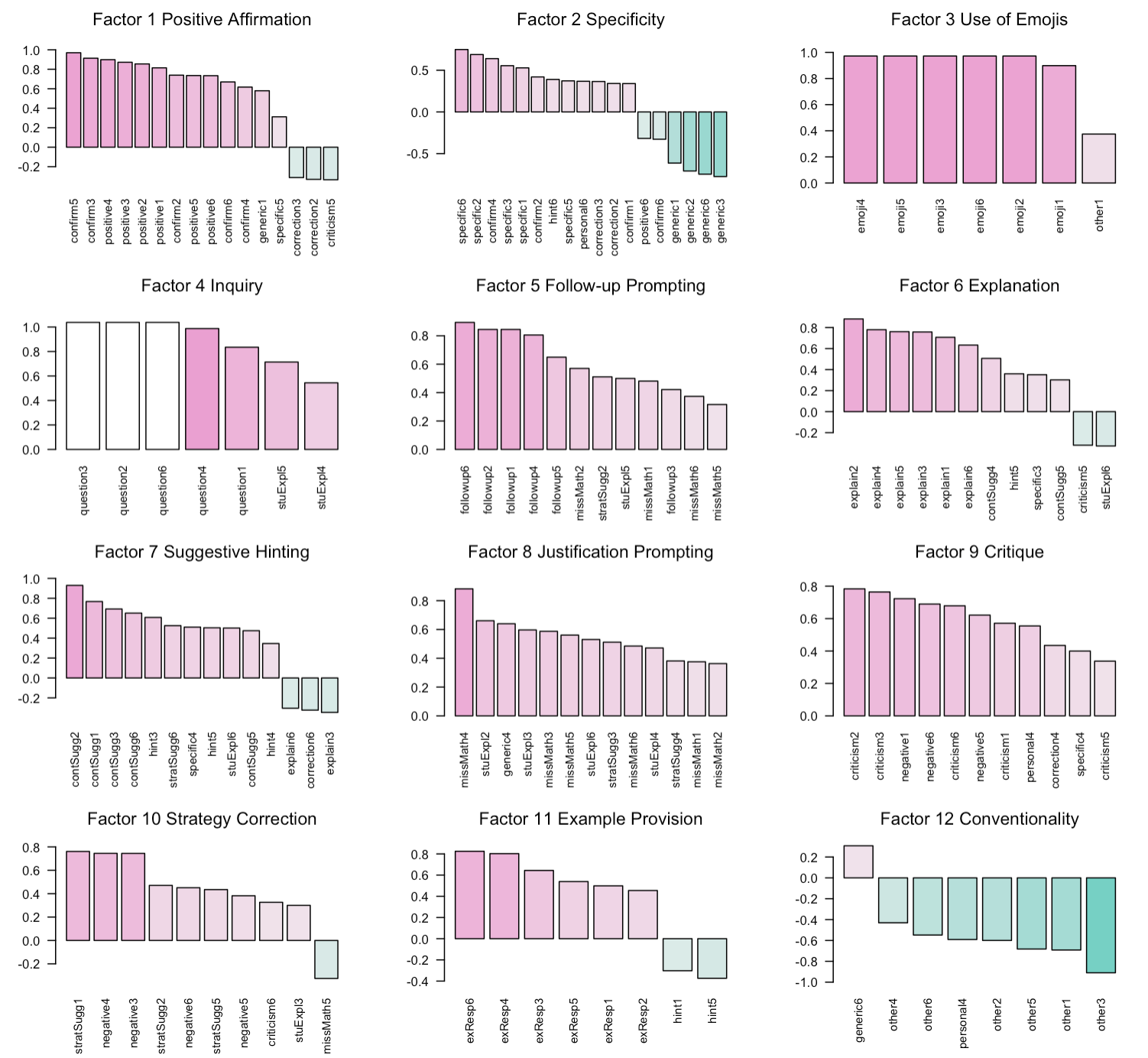
We identified 12 underlying factors which emerged from across the 114 codes (i.e., 19 characteristics times 6 coders). The results are presented in Figure 3, where each bar plot displays the highest-loading characteristics within a given factor. Most codes were loaded onto a factor with one or more other codes, with a few exceptions (i.e., Factors 3, 4, 6, and 12). For instance, six variables of the same code “Emoji” showed loadings higher than 0.8 for Factor 3. Similarly, Factor 4 had strong loadings from five variables of code “Question,” Factor 12 had strong loadings from six variables of “Other,” and Factor 6 of “Explanation,” suggesting high internal consistency. Notably, Factor 9 had strong loadings from five variables of “Criticism” and three of “Negative Affect,” indicating a potential overlap in how these codes are applied despite the differences in how they were initially operationalized. In Section 5, we discuss the remaining factors with loadings from different codes in relation to the research questions and how they contribute to the mapping the complex structure of feedback.
4.3. Results of the Cluster Analysis
As shown in Figure 4, we identified 10 clusters, each representing a distinct type of feedback content. To characterize these clusters, we report their most salient defining features, as represented by factor loadings from the exploratory factor analysis. These factors highlight patterns that are more pronounced within a given cluster relative to others. We present the clusters in descending order of size, reflecting the relative prevalence of each feedback type in the dataset.
As the largest cluster with 26 observations, Cluster 9 was defined by high values of Factor 11 “Example Provision” and Factor 6 “Explanation,” indicating a strong emphasis on providing students with concrete examples and detailed explanations to support conceptual understanding. The second-largest cluster was Cluster 10, with 16 observations. This cluster was marked by a positive value of Factor 1 “Positive Affirmation” and a negative value of Factor 2 “Specificity,” suggesting that this type of feedback is rich in encouragement and emotional support but lacks actionable guidance.
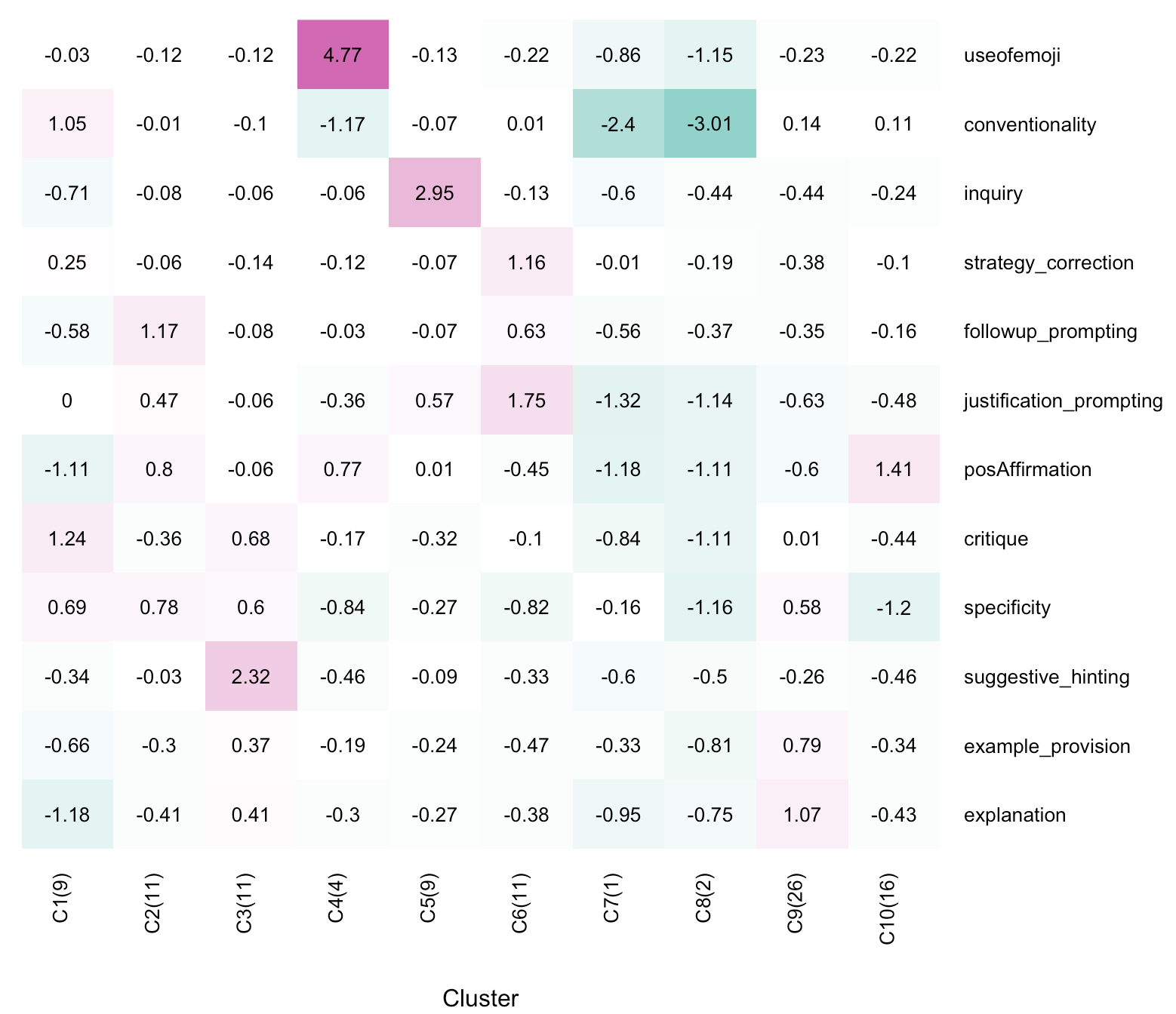
Next, five clusters had a comparable number of observations. Cluster 2 was characterized by Factor 5 “Follow-up Prompting,” Factor 1 “Positive Affirmation,” and Factor 2 “Specificity,” suggesting a feedback type that is sufficiently supportive but defers full clarification by asking students to follow up in person. Cluster 3 involved Factor 7 “Suggestive Hinting,” Factor 9 “Critique,” and Factor 2 “Specificity,” indicating a feedback strategy that scaffolds student understanding through subtle guidance without explicitly providing answers. Cluster 6 was distinguished by Factor 10 “Strategy Correction” and Factor 8 “Justification Prompting,” suggesting feedback to enhance students’ problem-solving approaches by encouraging them to explain their reasoning. Cluster 1 had high positive values of Factor 9 “Critique,” Factor 12 “Conventionality,” and Factor 2 “Specificity,” but high negative values of several features, such as Factor 4 “Inquiry,” Factor 5 “Follow-up Prompting,” and Factor 6 “Explanation.” This feedback type shows a traditional focus on identifying errors, but with minimal scaffolding. In comparison, Cluster 5 had a high positive value for Factor 4 “Inquiry,” indicating the use of rhetorical questions to encourage critical thinking and promote deeper student reflection.
The other clusters are composed of relatively few observations. Cluster 4, with four observations, showed high values of Factor 3 “Use of Emoji” and Factor 1 “Positive Affirmation,” indicating a heavy reliance on non-verbal emotional cues to convey encouragement. Cluster 7, based on a single observation, had negative values across all features, most notably in Factor 8 “Justification Prompting,” Factor 1 “Positive Affirmation,” and Factor 11 “Example Provision.” Similarly, Cluster 8, with two observations, had negative values across multiple features, with particularly low values in Factor 12 “Conventionality” and Factor 9 “Critique.” While the small sample sizes in these clusters warrant caution in interpretation, they may represent emerging feedback strategies that were not fully captured by our coding scheme.
5. Discussion
This study demonstrates the use of data mining methods to identify key types of teacher feedback on students’ open-ended responses. Across our analyses, we established a set of feedback clusters that were derived from a set of factors underlying our 19 coded feedback characteristics. This section examines these results in the context of our three research questions.
5.1. RQ1. How do perceptions and judgments of feedback characteristics vary among individuals with different backgrounds and experiences?
Notable variations emerged between how our two groups coded. Overall, divergent interpretations were more pronounced for context-dependent codes such as “Hints” compared to more clear-cut codes like “Question.” However, certain context-dependent codes, such as “Negative Affect” and “Example Response,” exhibited higher agreement among teacher coders than among researchers. Given that researchers were involved in the initial code development, such discrepancies suggest that the variations may reflect domain-specific experiences rather than coder training alone. This finding aligns with prior research indicating that teachers often rely on distinct rubrics shaped by their professional knowledge and experience (e.g., Meier et al. 2006), further reflecting how coders’ individual interpretations of the coding schema and the given data can influence coding practices (e.g., Belur et al. 2021).
Several distinct correlation patterns were observed between researchers and teachers. Within the researcher group, “Specific” was strongly correlated with both “Correction” and “Explanation,” whereas in the teacher group, “Mathematical Suggestions” was correlated with both “Specific” and “Explanation.” One interpretation of this difference is that researchers consider specificity in terms of the extent to which feedback helped clarify students’ understanding through corrective or elaborated feedback. Teachers, by contrast, focus on the degree of mathematical relevance and details in feedback to promote students’ mathematical knowledge and skills. Differences also emerged in how researchers and teachers qualitatively coded “Student Explanation.” Among researchers, this code was most strongly associated with “Learning Strategy Suggestion,” indicating a focus on guiding students toward effective problem-solving approaches. For teachers, it correlated more with “Question” and “No Mathematics,” reflecting an emphasis on prompting students for further clarification or identifying missing mathematical content.
Overall, the findings suggest that each group’s interpretative lens is shaped by their professional backgrounds and experiences. For researchers, the emphasis was on the diagnostic function of feedback, while for teachers, it centered on pedagogical design underlying the feedback. Understanding these differences offers a more nuanced perspective on how feedback is constructed and interpreted by different stakeholders, providing a foundation for more comprehensive frameworks that can bridge these perspectives in future research and practice.
5.2. RQ2. What underlying factors emerge across varying perceptions and judgments of the feedback characteristics?
The factor analysis revealed several groupings of codes with strong loadings, suggesting that latent constructs formed by different codes can provide insights into how distinct features combine and contribute to a nuanced understanding of feedback. Three factors had two or more codes loaded with primarily positive values (i.e., Factors 5, 8, and 9). For example, Factor 5, which we refer to as Follow-up Prompting, included “Follow-up” (N=7) and “No Mathematics” (N=3), suggesting that feedback at this dimension involved teachers taking a more proactive measure to address significant lack of mathematical work in students’ response. Similarly, Factor 8 Justification Prompting included “No Mathematics” (N=6) and “Student Explanation” (N=4), suggesting that this dimension of feedback encourages students to articulate reasoning when their responses are under-developed.
Several factors had both positive and negative loadings, indicating inverse relationships among codes within the construct. In some cases, these relationships were consistent with the underlying logic of the coding scheme. For instance, Factor 1 Positive Affirmation included strong positive loadings from “Positive Affect” (N=6) and “Confirmation” (N=5) and negative loadings from “Correction” (N=2). Similarly, Factor 2 Specificity had positive loadings from “Specific” (N=5) and “Confirmation” (N=3) and negative loadings from “Generic” (N=4). Interestingly, Factor 10 Strategy Correction had strong positive loadings from “Negative Affect” (N=4), and “Learning Strategy Suggestion” (N=3), suggesting that this dimension of feedback involves teachers recommending strategic learning approaches, often prompted by a negative evaluation of the student’s response.
In other cases, the inverse relationships among codes highlighted subtle distinctions between constructs that likely reflect different instructional goals. For example, Factor 7 Suggestive Hinting included positive loadings from “Mathematical Suggestions” (N=4) and “Hint” (N=3) but negative loadings from “Explanation” (N=2). On the other hand, Factor 11 Example Provision included positive loadings from “Example Response” (N=6) and negative loadings from “Hint” (N=2). The different directions of loadings for hint underscores how it functions as a more indirect form of support without explicitly providing the near-complete solution.
5.3. RQ3. What types of feedback content emerge from the measured factors?
As part of our initial goal, we present a taxonomy with 10 distinct types of feedback content that teachers provide in the context of middle school mathematics. Table 3 summarizes each cluster using descriptive labels that characterize the feedback type and provides illustrative examples drawn from the dataset. This data-driven taxonomy illustrates how core dimensions of teacher feedback can combine to reveal distinct patterns of instructional practice.
| Cluster | Type of Feedback | Example |
|---|---|---|
| 1 | Direct Correction | “Missing one X above 2 1/4.”; “You did not complete the table.” |
| 2 | Targeted Affirmation | “Good start, but you should include how many classes the slope shows you can attend for that price.” |
| 3 | Hinting | “Very nice drawing. Make sure you multiply the numerator and denominator.” |
| 4 | Non-verbal Affirmation | “:)” |
| 5 | Rhetorical Question | “You are on the right track. What about the 6’s inside the boxes in the tape diagram?” |
| 6 | Show Your Work | “Show what you were thinking. You can use the correct answer to help you show the work for the correct answer.” |
| 7 | Generic Comment | “Keep trying.” |
| 8 | Direct Critique | “You need to improve your explanation.” |
| 9 | Worked Example | “12 is correct. You would get 3/12 + 2/12, which would give you an answer of 5/12.” |
| 10 | Non-specific Positivity | “Great job!”; “You got it!” |
The majority of the feedback centered on various forms of scaffolding, or strategies oriented towards playing a facilitative role, such as “Hinting,” “Rhetorical Question,” “Show Your Work,” and “Worked Example.” These strategies can be used to prompt students to rethink their problem-solving processes by respectively posing thought-provoking questions, requesting explanations of their thought processes, or presenting exemplars. This categorization offers a more nuanced perspective than Shute (2008), which broadly frames elaborated feedback as guidance that directs learners without explicitly presenting the correct answer. However, it similarly includes prompts, hints, and examples as different ways of guiding students’ next steps.
Another set of feedback types includes different types of responses regarding the correctness of student answers. For example, “Direct Correction” focuses on identifying specific errors and providing corrective guidance. While this type of feedback may provide limited opportunities for deeper reflection, it can offer more concrete direction than other types such as “Direct Critique” or “Generic Comment,” where lack of specificity can add uncertainty, frustration, or cognitive load on students (Shute, 2008). Affirmation feedback is further differentiated into “Targeted Affirmation,” “Non-specific Positivity,” and “Non-verbal Affirmation,” each varying in its degree of specificity or modality. Rather than treating all correctness-related feedback as a single category as in Narciss (2013), our taxonomy delineates subtle distinctions between these subtypes.
In summary, the taxonomy, grounded in authentic contexts, highlights subtle yet important differences in how teachers confirm correctness, provide corrective guidance, or scaffold student thinking, illustrating the nuanced ways feedback operates in practice.
6. Implications for Research and Practice
This taxonomy has implications for both research and practice. By categorizing feedback content in systematic and interpretable ways for both researchers and teachers, the taxonomy establishes a shared language to discuss, evaluate, and refine feedback practices. When integrated into learning systems, the taxonomy can support teachers in delivering feedback that is not only pedagogically meaningful but also more consistent, thereby reducing the variability often associated with human-authored feedback at scale. Also, the taxonomy provides researchers with a structured foundation to investigate the effects of specific feedback types on learning outcomes and to examine their function across varied instructional contexts and student populations. By fostering stronger alignment between research and practice, this taxonomy can support the delivery of feedback that is timely, pedagogically grounded, and responsive to the learner’s needs.
7. Limitations and Future Work
This work has several limitations that can be addressed in future work. First, while the data were drawn from a widely used learning platform, the scope of this study was confined to teacher-written feedback in middle school mathematics. As the methodological approach taken in this study offers a means for identifying broader patterns in feedback structure and developing a data-driven taxonomy, future work can examine its generalizability to other subject areas, grade levels, and instructional modalities beyond web-based learning platforms. Broadening the scope of inquiry in these directions would also strengthen the robustness of the taxonomy, and improve its practical utility for both researchers and practitioners across diverse educational domains and settings.
Second, this study considered potential differences in how various stakeholders, such as researchers and teachers, interpret teacher feedback; however, it did not account for students, who are the primary agents of learning. While this study focused on teacher-authored messages, it is equally important to understand how students perceive and act on feedback (e.g., Ryan et al. 2021). Future research should involve students in the design and evaluation process to ensure that feedback is interpreted as intended and fulfills its purpose of serving learners. Given that the effectiveness of feedback varies across students (Dawson et al., 2019), involving students as stakeholders can help ensure that the feedback delivered, whether by teachers or AI, is both interpretable and actionable, ultimately promoting student learning.
Finally, while this paper does not directly propose a system for automated feedback generation, it is motivated by the need to support scalable approaches to evaluating feedback through a principled understanding of feedback types. One promising direction for future research concerns the integration of large language models to support the generation and evaluation of feedback. Prior work has explored the use of natural language processing and clustering techniques to facilitate scalable feedback and assessment (Basu et al., 2013, Brooks et al., 2014, Zhao et al., 2017, Botelho et al., 2023). However, these systems often lack frameworks grounded in human-in-the-loop design principles, which limits their interpretability and pedagogical relevance (Bhutoria, 2022, Monarch, 2021). The taxonomy developed in this study provides an empirically grounded foundation for informing the design and evaluation of LLM-based feedback systems. Specifically, the identified feedback types may be used to guide prompt engineering, fine-tuning objectives, or evaluation criteria, helping to ensure that generated feedback aligns with authentic instructional goals and classroom practice.
8. Conclusion
In this paper, we proposed and implemented a discovery-oriented modeling pipeline for developing a taxonomy of teacher-authored feedback in response to open-ended mathematics problems. This study contributes to the growing conversation around scaling effective feedback in the design of educational technologies. By allowing different teachers’ feedback types or their interpretations to be represented as distinct features within our approach, our work seeks to preserve the complex decision-making processes and perceptions involved in designing feedback. We argue that this type of data-driven, context-aware taxonomy offers a practical foundation for understanding and generating feedback at scale. In doing so, it supports the development of AI-enhanced systems that can deliver feedback that is not only timely but also pedagogically meaningful. As such, this study lays the groundwork for future work on feedback evaluation, classification, and generation that reflects the realities of classroom teaching.
9. Acknowledgments
We would like to thank the journal editors and anonymous reviewers for their thoughtful feedback throughout the review process. Also, we extend our sincere gratitude to the National Science Foundation (NSF) for their generous support through grants 2331379, 1903304, 1822830, and 1724889, the Institute of Education Sciences (IES) through grant R305B230007, as well as Schmidt Futures and MathNet.
Declaration of Generative AI in the Writing Process
We would also like to acknowledge the assistance provided by ChatGPT during the preparation of this work. Specifically, we used it to improve the grammar and clarity of our initial drafts. All content was thoroughly reviewed and edited by human authors prior to submission.
References
- Abdu Saeed Mohammed, M. and Abdullah Alharbi, M. 2022. Cultivating learners’ technology-mediated dialogue of feedback in writing: Processes, potentials and limitations. Assessment & Evaluation in Higher Education 47, 6, 942–958.
- Aleven, V., McLaughlin, E. A., Glenn, R. A., and Koedinger, K. R. 2016. Instruction based on adaptive learning technologies. Handbook of Research on Learning and Instruction 2, 522–560.
- Anderson, R. C. and Biddle, W. B. 1975. On asking people questions about what they are reading. In Psychology of Learning and Motivation, G. H. Bower, Ed. Vol. 9. Academic Press, New York, NY, 89–132.
- Bahar, A. and Maker, C. J. 2015. Cognitive backgrounds of problem solving: A comparison of open-ended vs. closed mathematics problems. Eurasia Journal of Mathematics, Science and Technology Education 11, 6, 1531–1546.
- Baker, R. S., Corbett, A. T., and Koedinger, K. R. 2004. Detecting student misuse of intelligent tutoring systems. In Intelligent Tutoring Systems: 7th International Conference, ITS 2004, Maceió, Alagoas, Brazil, August 30-September 3, 2004. Proceedings 7. Springer, 531–540.
- Baker, R. S. d., Corbett, A. T., Gowda, S. M., Wagner, A. Z., MacLaren, B. A., Kauffman, L. R., Mitchell, A. P., and Giguere, S. 2010. Contextual slip and prediction of student performance after use of an intelligent tutor. In User Modeling, Adaptation, and Personalization: 18th International Conference, UMAP 2010, Big Island, HI, USA, June 20-24, 2010. Proceedings 18. Springer, 52–63.
- Barabasheva, I. 2021. Feedback as a means of motivation in foreign language teaching. In LATIP 2021: International Conference on Language and Technology in the Interdisciplinary Paradigm. European Proceedings of Social and Behavioural Sciences, vol. 121. European Publisher, Future Academy, London, UK, 221–227.
- Baral, S., Botelho, A. F., Erickson, J. A., Benachamardi, P., and Heffernan, N. T. 2021. Improving automated scoring of student open responses in mathematics. International Educational Data Mining Society, 130–138.
- Baral, S., Santhanam, A., Botelho, A., Gurung, A., and Heffernan, N. 2023. Automated scoring of image-based responses to open-ended mathematics question. In Proceedings of the 16th International Conference on Educational Data Mining (EDM). International Educational Data Mining Society, Bengaluru, India, 362––369.
- Baral, S., Worden, E., Lim, W.-C., Luo, Z., Santorelli, C., and Gurung, A. 2024. Automated assessment in math education: A comparative analysis of LLMs for open-ended responses. In Proceedings of the 17th International Conference on Educational Data Mining, B. Paaßen and C. D. Epp, Eds. International Educational Data Mining Society, Atlanta, Georgia, USA, 732–737.
- Basu, S., Jacobs, C., and Vanderwende, L. 2013. Powergrading: A clustering approach to amplify human effort for short answer grading. Transactions of the Association for Computational Linguistics 1, 391–402.
- Belur, J., Tompson, L., Thornton, A., and Simon, M. 2021. Interrater reliability in systematic review methodology: Exploring variation in coder decision-making. Sociological Methods & Research 50, 2, 837–865.
- Bhutoria, A. 2022. Personalized education and artificial intelligence in the United States, China, and India: A systematic review using a human-in-the-loop model. Computers and Education: Artificial Intelligence 3, 100068.
- Bisra, K., Liu, Q., Nesbit, J. C., Salimi, F., and Winne, P. H. 2018. Inducing self-explanation: A meta-analysis. Educational Psychology Review 30, 703–725.
- Boaler, J. 1998. Open and closed mathematics: Student experiences and understandings. Journal for Research in Mathematics Education 29, 1, 41–62.
- Botelho, A. F., Baral, S., Erickson, J. A., Benachamardi, P., and Heffernan, N. T. 2023. Leveraging natural language processing to support automated assessment and feedback for student open responses in mathematics. Journal of Computer Assisted Learning 39, 3, 823–840.
- Boyer, K. E., Phillips, R., Wallis, M., Vouk, M., and Lester, J. 2008. Balancing cognitive and motivational scaffolding in tutorial dialogue. In Intelligent Tutoring Systems: 9th International Conference, ITS 2008, Montreal, Canada, June 23-27, 2008 Proceedings 9. Springer, 239–249.
- Brooks, M., Basu, S., Jacobs, C., and Vanderwende, L. 2014. Divide and correct: Using clusters to grade short answers at scale. In Proceedings of the First ACM Conference on Learning@ Scale. 89–98.
- Cheng, L., Hampton, J., and Kumar, S. 2022. Engaging students via synchronous peer feedback in a technology-enhanced learning environment. Journal of Research on Technology in Education 56, sup1, 347–371.
- Chi, M. T., De Leeuw, N., Chiu, M.-H., and LaVancher, C. 1994. Eliciting self-explanations improves understanding. Cognitive Science 18, 3, 439–477.
- Chi, M. T. H. 2000. Self-explaining expository texts: The dual processes of generating inferences and repairing mental models. In Advances in Instructional Psychology, Volume 5, R. Glaser, Ed. Routledge, New York, NY, 161–238.
- Coburn, C. E. and Turner, E. O. 2012. The practice of data use: An introduction. American Journal of Education 118, 2, 99–111.
- Corbett, A. T. and Anderson, J. R. 1994. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-adapted Interaction 4, 253–278.
- Corral, D. and Carpenter, S. K. 2020. Facilitating transfer through incorrect examples and explanatory feedback. Quarterly Journal of Experimental Psychology 73, 9, 1340–1359.
- Dawson, P., Henderson, M., Mahoney, P., Phillips, M., Ryan, T., Boud, D., and Molloy, E. 2019. What makes for effective feedback: Staff and student perspectives. Assessment & Evaluation in Higher Education 44, 1, 25–36.
- Erickson, J. A., Botelho, A. F., McAteer, S., Varatharaj, A., and Heffernan, N. T. 2020. The automated grading of student open responses in mathematics. In Proceedings of the Tenth International Conference on Learning Analytics & Knowledge. 615–624.
- Feng, M., Huang, C., and Collins, K. 2023. Promising long term effects of assistments online math homework support. In International Conference on Artificial Intelligence in Education. Springer, 212–217.
- Fong, C. J. and Schallert, D. L. 2023. “Feedback to the future”: Advancing motivational and emotional perspectives in feedback research. Educational Psychologist 58, 3, 146–161.
- Gaddipati, S. K., Nair, D., and Plöger, P. G. 2020. Comparative evaluation of pretrained transfer learning models on automatic short answer grading. arXiv preprint arXiv:2009.01303.
- Gan, Z., An, Z., and Liu, F. 2021. Teacher feedback practices, student feedback motivation, and feedback behavior: How are they associated with learning outcomes? Frontiers in Psychology 12, 697045.
- Grawemeyer, B., Mavrikis, M., Holmes, W., Gutiérrez-Santos, S., Wiedmann, M., and Rummel, N. 2017. Affective learning: Improving engagement and enhancing learning with affect-aware feedback. User Modeling and User-Adapted Interaction 27, 119–158.
- Gurung, A., Baral, S., Lee, M. P., Sales, A. C., Haim, A., Vanacore, K. P., McReynolds, A. A., Kreisberg, H., Heffernan, C., and Heffernan, N. T. 2023. How common are common wrong answers? crowdsourcing remediation at scale. In Proceedings of the Tenth ACM Conference on Learning@ Scale. 70–80.
- Gusukuma, L., Bart, A. C., Kafura, D., and Ernst, J. 2018. Misconception-driven feedback: Results from an experimental study. In Proceedings of the 2018 ACM Conference on International Computing Education Research. 160–168.
- Hargreaves, E. 2014. The practice of promoting primary pupils’ autonomy: Examples of teacher feedback. Educational Research 56, 3, 295–309.
- Hattie, J. and Timperley, H. 2007. The power of feedback. Review of Educational Research 77, 1, 81–112.
- Hauke, J. and Kossowski, T. 2011. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaestiones Geographicae 30, 2, 87–93.
- Heffernan, N. T. and Heffernan, C. L. 2014. The ASSISTments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education 24, 470–497.
- Hou, W.-J. and Tsao, J.-H. 2011. Automatic assessment of students’ free-text answers with different levels. International Journal on Artificial Intelligence Tools 20, 02, 327–347.
- Klein, R., Kyrilov, A., and Tokman, M. 2011. Automated assessment of short free-text responses in computer science using latent semantic analysis. In Proceedings of the 16th Annual Joint Conference on Innovation and Technology in Computer Science Education. 158–162.
- Kluger, A. N. and DeNisi, A. 1996. The effects of feedback interventions on performance: a historical review, a meta-analysis, and a preliminary feedback intervention theory. Psychological Bulletin 119, 2, 254.
- Konold, K. E., Miller, S. P., and Konold, K. B. 2004. Using teacher feedback to enhance student learning. Teaching Exceptional Children 36, 6, 64–69.
- Kulik, J. A. and Kulik, C.-L. C. 1988. Timing of feedback and verbal learning. Review of Educational Research 58, 1, 79–97.
- Kwon, O. N., Park, J. H., and Park, J. S. 2006. Cultivating divergent thinking in mathematics through an open-ended approach. Asia Pacific Education Review 7, 51–61.
- Labuhn, A. S., Zimmerman, B. J., and Hasselhorn, M. 2010. Enhancing students’ self-regulation and mathematics performance: The influence of feedback and self-evaluative standards. Metacognition and learning 5, 173–194.
- Lee, H.-S., Pallant, A., Pryputniewicz, S., Lord, T., Mulholland, M., and Liu, O. L. 2019. Automated text scoring and real-time adjustable feedback: Supporting revision of scientific arguments involving uncertainty. Science Education 103, 3, 590–622.
- Madnani, N., Burstein, J., Sabatini, J., and O’Reilly, T. 2013. Automated scoring of summary-writing tasks designed to measure reading comprehension. Grantee Submission.
- McNamara, D. S., Crossley, S. A., Roscoe, R. D., Allen, L. K., and Dai, J. 2015. A hierarchical classification approach to automated essay scoring. Assessing Writing 23, 35–59.
- McNichols, H., Lee, J., Fancsali, S., Ritter, S., and Lan, A. 2024. Can large language models replicate ITS feedback on open-ended math questions? In Proceedings of the 17th International Conference on Educational Data Mining, B. Paaßen and C. D. Epp, Eds. International Educational Data Mining Society, Atlanta, Georgia, USA, 769–775.
- Meier, S. L., Rich, B. S., and Cady, J. 2006. Teachers’ use of rubrics to score non-traditional tasks: Factors related to discrepancies in scoring. Assessment in Education 13, 01, 69–95.
- Monarch, R. M. 2021. Human-in-the-Loop Machine Learning: Active learning and annotation for human-centered AI. Simon and Schuster.
- Moreno, R. 2004. Decreasing cognitive load for novice students: Effects of explanatory versus corrective feedback in discovery-based multimedia. Instructional Science 32, 1, 99–113.
- Mory, E. H. 2013. Feedback research revisited. In Handbook of Research on Educational Communications and Technology, J. M. Spector, M. D. Merrill, J. Elen, and M. J. Bishop, Eds. Routledge, New York, NY, 738–776.
- Munroe, L. 2015. The open-ended approach framework. European Journal of Educational Research 4, 3, 97–104.
- Narciss, S. 2013. Designing and evaluating tutoring feedback strategies for digital learning. Digital Education Review 23, 7–26.
- Narciss, S., Sosnovsky, S., Schnaubert, L., Andrès, E., Eichelmann, A., Goguadze, G., and Melis, E. 2014. Exploring feedback and student characteristics relevant for personalizing feedback strategies. Computers & Education 71, 56–76.
- Navarro-Gonzalez, D. and Lorenzo-Seva, U. 2021. EFA.MRFA: Dimensionality Assessment Using Minimum Rank Factor Analysis. R package.
- Qi, H., Wang, Y., Dai, J., Li, J., and Di, X. 2019. Attention-based hybrid model for automatic short answer scoring. In Simulation Tools and Techniques: 11th International Conference, SIMUtools 2019, Chengdu, China, July 8–10, 2019, Proceedings 11. Springer, 385–394.
- Rau, M. A., Aleven, V., and Rummel, N. 2015. Successful learning with multiple graphical representations and self-explanation prompts. Journal of Educational Psychology 107, 1, 30.
- Ryan, T., Henderson, M., Ryan, K., and Kennedy, G. 2021. Designing learner-centred text-based feedback: A rapid review and qualitative synthesis. Assessment & Evaluation in Higher Education 46, 6, 894–912.
- Sadler, D. R. 1989. Formative assessment and the design of instructional systems. Instructional Science 18, 2, 119–144.
- Saldaña, J. 2021. The coding manual for qualitative researchers. SAGE publications Ltd.
- Shute, V. J. 2008. Focus on formative feedback. Review of Educational Research 78, 1, 153–189.
- Sweller, J. 2011. Cognitive load theory. In Psychology of Learning and Motivation, B. H. Ross, Ed. Vol. 55. Elsevier, San Diego, CA, 37–76.
- Taghipour, K. and Ng, H. T. 2016. A neural approach to automated essay scoring. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing. 1882–1891.
- Thompson, D. R. and Senk, S. L. 1998. Implementing the assessment standards for school mathematics: Using rubrics in high school mathematics courses. The Mathematics Teacher 91, 9, 786–793.
- Van der Kleij, F. M., Feskens, R. C., and Eggen, T. J. 2015. Effects of feedback in a computer-based learning environment on students’ learning outcomes: A meta-analysis. Review of Educational Research 85, 4, 475–511.
- Vanacore, K., Gurung, A., Sales, A., and Heffernan, N. T. 2024. The effect of assistance on gamers: Assessing the impact of on-demand hints & feedback availability on learning for students who game the system. In Proceedings of the 14th Learning Analytics and Knowledge Conference. 462–472.
- Wisniewski, B., Zierer, K., and Hattie, J. 2020. The power of feedback revisited: A meta-analysis of educational feedback research. Frontiers in Psychology 10, 487662.
- Wylie, R. and Chi, M. T. H. 2014. The self-explanation principle in multimedia learning. In The Cambridge Handbook of Multimedia Learning, R. E. Mayer, Ed. Cambridge University Press, Cambridge, UK, 413–432.
- Yang, M. and Carless, D. 2013. The feedback triangle and the enhancement of dialogic feedback processes. Teaching in Higher Education 18, 3, 285–297.
- Zhao, S., Zhang, Y., Xiong, X., Botelho, A., and Heffernan, N. 2017. A memory-augmented neural model for automated grading. In Proceedings of the Fourth (2017) ACM Conference on Learning@ Scale. 189–192.
*Both authors made equally substantial contributions to this research.
1While our data cannot be publicly shared, all analysis code, as well as instructions for establishing a data sharing agreement,
are provided through OSF: https://osf.io/puhyr/?view_only=514d8534e9be41d9a57ad82e9efb3249
2Fleiss’ Kappa for this code was computed for the teacher group but is undefined for the research team and combined groups, as no researcher applied the code.
3We used the EFA.MRFA package by Navarro-Gonzalez and Lorenzo-Seva (2021).