Abstract
In higher education, academic advising is crucial to students’ decision-making. Data-driven models can benefit students in making informed decisions by providing insightful recommendations for completing their degrees. To suggest courses for the upcoming semester, various course recommendation models have been proposed in the literature using different data mining techniques and machine learning algorithms utilizing different data types. One important aspect of the data is that usually, courses taken together in a semester fit well with each other. If there is no correlation between the co-taken courses, students may find it more difficult to handle the workload. Based on this insight, we propose using session-based approaches to recommend a set of well-suited courses for the upcoming semester. We test three session-based course recommendation models, two based on neural networks (CourseBEACON and CourseDREAM) and one on tensor factorization (TF-CoC). Additionally, we propose a post-processing approach to adjust the recommendation scores of any base course recommender to promote related courses. Using metrics capturing different aspects of the recommendation quality, our experimental evaluation shows that session-based methods outperform existing popularity-based, association-based, similarity-based, factorization-based, neural networks-based, and Markov chain-based recommendation approaches. Effective course recommendations can result in improved student advising, which, in turn, can improve student performance, decrease dropout rates, and a more positive overall student experience and satisfaction.Keywords
1. Introduction
One of the challenges faced by undergraduate students is figuring out which courses to take each semester in order to effectively advance toward their degree. Students take into account a variety of factors when choosing their courses, such as keeping a balance between their degree program requirements and their personal preferences, interests, goals, and career aspirations. In each semester, a student needs to register for some elective or required courses that are offered by each department and there are some prerequisites for taking some courses. Making these choices is very difficult, so choosing the right courses is a non-trivial task for the students. Students may get help from the example guides or course catalog provided by the department, but the suggestions are generalized and not adapted to provide personalized recommendations to each student (Diamond et al., 2014). They may also get suggestions from other, possibly more senior, students. However, these opinions would be based on other students’ own experiences, preferences, and background, and may not be helpful to students with different backgrounds or goals. Academic advisors can provide individualized support and personalized recommendations to each student. However, the ratio of students to advisors is very high usually in most departments which limits the time and attention that an advisor can spend on a single student (Kadlec et al., 2014). Because of a lack of communication and proper guidance, many students may make wrong decisions and find themselves in difficult situations where they are unable to keep up with the course workload, become frustrated during the semester, and take more courses than needed overall. Consequently, the dropout rates at the undergraduate level of US colleges and universities are increasing and alarming (Hanson, 2022).
The advancement of machine learning models and data mining techniques can facilitate student advising by extracting valuable insights from past data records and producing personalized course recommendations for each student. In this area of study, collaborative filtering algorithms and content-based filtering techniques are the most widely used methodologies (Esteban et al., 2018, Pardos and Jiang, 2020, Polyzou et al., 2019, Shao et al., 2021). Existing research has examined the sequential nature of course enrollment data (student-course interactions over semesters) of past students, the vocabulary and topics linked to course description data, the ranking of students’ preferences for one course over another course, conducting surveys to understand students’ skills, preferences and career goals, and assessing their characteristics to recommend courses for the next semester or multiple consecutive semesters. Nevertheless, no previous research has been done in the literature that considers the synergy of the courses taken together. When two courses cover complementary and related concepts, they are typically taken together and students perform well in those courses. Additionally, students usually avoid taking multiple extremely heavy and unrelated courses in the same semester. If students enroll in three or four difficult courses during a single semester, they may not have enough time to prepare for each course, which could result in poor performance in some or all of them. Their final semester grade point average (GPA) may become very low although they put in lots of effort. On the contrary, if students’ courses are related to one another and manageable to complete within a semester, they may perform better. Course choices are positively associated with students’ academic performances (Gong et al., 2024).
Co-taken courses, or the set of courses taken in a semester by past students, can offer insightful information about the compatibility, correlation, and relationship between each pair of courses. These notions can be captured by using session-based recommendation approaches. We propose to adapt such approaches to rank courses according to both their suitability and synergy and recommend well-suited courses for the next semester. The courses taken semester by semester have long-term and short-term dependencies that we can capture with deep learning models.
We explore two distinct models that capture these dependencies in two different ways. First, the CourseBEACON model captures and determines the relationship between each pair of courses by computing the co-occurrence rate. Then, the recommendation task is carried out by integrating this concept of course compatibility into a sequential deep learning model (a type of recurrent neural network (RNN) that captures long short-term dependencies of items). Second, in CourseDREAM, we create a latent vector representation for each set of courses taken within a semester that can also capture the courses that are historically considered well-suited to be taken in the same semester. Then, we use the same variant of RNN to capture the sequential transitions semester-by-semester. Additionally, we explore the use of tensor factorization to capture the relationship between co-taken courses. Finally, we propose an approach to adjust the correlation of the set of recommended courses as a post-processing step.
Using real historical enrollment data of past students, we evaluate these proposed approaches. We also compare them against a variety of other competing approaches such as popularity-based baselines, association-based, similarity-based, factorization-based, neural networks (NeuralNet), and Markov chain-based models that are proposed in the literature using students’ course enrollment data. We compute different evaluation metrics to measure the suitability of recommended courses that will be taken together in a semester. We also create different visualizations to better understand the suitability of recommended courses. Our proposed approaches outperform other baselines or existing state-of-the-art competing approaches.
The paper is organized as follows: Section 2 introduces the background and notation, and Section 3 presents the related work, while Section 4 delves deeper into the proposed approaches. Section 5 presents our experimental setup and competing approaches in detail. Section 6 discusses the results and insights gained while Section 7 summarizes and concludes the paper.
2. Background
2.1. Problem
Students need to take several courses to earn their degree. While it might differ across departments and universities, in the US, students are usually free to decide which courses to take within a semester and in which semester to take any required courses. During course selection, students must remember degree requirements and several other factors such as course prerequisites, personal preferences, career goals, and which courses are needed to build knowledge for future courses. So, course selection and planning is a difficult task. Universities naturally collect information about the course registration history of students, which can be analyzed to extract insightful patterns to recommend courses to future students. Course recommendation (CR) is a systematic way to evaluate which courses are appropriate for a student to register for in an upcoming semester. We do that by inspecting the student-course interactions and the sequential transitions of courses over the semesters of past students.
We make the following assumptions in the context of course recommendation. Time is discrete and moves from one semester to the next. There is no order in the courses within a semester, but they are ordered across semesters (e.g., courses taken in the first semester, second semester, etc.). Learning is sequential, with each course taken during a semester imparting knowledge and skills that will be useful for subsequent courses. So, the order in which courses are taken usually matters. When enough domain experts are unavailable, students’ course registration histories may offer useful insight into the curriculum and degree requirements. Finally, we assume that a student wants to take a specific number of courses next semester.
2.2. Definition of Terms and Notations
Considering the terminology used in general recommendation literature, we can consider each student and course as a user and an item, respectively.
A session is a limited period of time during which a user does some tasks together. In this paper, a student’s semester represents a session. In a single session, a user can select a collection of items. In our context, a student will take some courses together in a semester. A set of items (courses) in a session make a basket. In session-based recommendation models, users’ preferences are learned by analyzing the items associated with each session. More attention is placed on recent sessions as users’ preferences evolve and change dynamically. A session-based recommendation system can recommend a list of items for the following session, for which we might or might not have some partial information (i.e., any items that have already been known in that session). A next basket recommendation is a special case when we generate an entire set of items for the next session without any partial information about that session. In this paper, we will recommend a complete set of courses (basket) for the next semester.
We adopt the following notation. We will use capital bold letters for matrices or tensors, calligraphic letters for sets, and lowercase bold letters for vectors. \(\mathcal {C}\) indicates the set of all courses (\(|\mathcal {C}|= m\)) and \(\mathcal {S}\) denotes the set of all students (\(|\mathcal {S}|=n\)). \(\mathcal {B}_{i,t}\) represents a set of courses that \(i\)-th student has taken in a semester \(t\). \(H_i\) is the course registration history of the \(i\)-th student, \( H_i = [\mathcal {B}_{i,1}, \mathcal {B}_{i,2},...,\mathcal {B}_{i,t_i}]\), where \(t_i = |H_i|\) is the total number of semesters that the \(i\)-th student took courses. We will refer to the student and the semester we are trying to generate a recommendation for as the target student and semester, respectively. Additional notation is presented in Table 1.
| \(\mathcal {C}\), \(\mathcal {S}\) | set of courses and students, respectively |
|---|---|
| \(m\), \(n\) | cardinality of \(\mathcal {C}\), \(\mathcal {S}\), \(|\mathcal {C}|=m\) and \(|\mathcal {S}|=n\) |
| \(p\), \(q\) | courses, \(p, q \in \mathcal {C}\) |
| \(u\) | student, \(u \in \mathcal {S}\) |
| \(i\), \(j\) | index for student and course, respectively |
| \(t\) | index for semester |
| \(\mathcal {B}_{i,t}\) | set of courses \(i\)-th student took in semester \(t\) |
| \(H_i\) | course registration history of \(i\)-th student |
| \(t_i\) | total number of semesters for \(i\)-th student, \(t_i=|H_i|\) |
| \(k\) | total number of courses to recommend |
| \(\mathbf {R}\) | tensor \(\mathbf {R} \in \mathbb {R}^{d \times d \times n} \) with \(d\) latent dimensions |
| \(\mathbf {F}_{i,p,q}\) | number of \((i, p, q)\) triples for \(i\)-th student |
3. Related Work
3.1. Data Sources for CR
Course recommendation systems (CRS) have been commonly built within traditional universities by using student enrollment information collected in their data warehouses (Al-Badarenah and Alsakran, 2016, Esteban et al., 2018, Pardos and Jiang, 2020, Polyzou et al., 2019, Shao et al., 2021, Wong, 2018). Online course platforms (such as edX and Moodle) can also benefit from CRS (De Medio et al., 2020, Obeidat et al., 2019, Zhang et al., 2018). To recommend online courses, association rule mining, sequential pattern mining (SPM) (Obeidat et al., 2019), and a combination of deep convolutional neural networks and negative SPM (Gao et al., 2022) have been proposed. In an online setting, Zhang et al. (2019) propose a hierarchical reinforcement learning (RL) model to remove noisy courses from users’ profiles and then fine-tune an attention-based neural networks model. Moreover, student feedback collected by conducting surveys is sometimes used (Esteban et al., 2018, Pardos and Jiang, 2020). A few researchers consider students’ interests and skills to build their models (Ma et al., 2021, Sulaiman et al., 2020). Constraint-based approaches focus on satisfying degree, departmental, and other complex requirements and constraints to recommend courses (Parameswaran et al., 2011). Additionally, the instructor can be a factor influencing course selection. However, few works consider this information in their models (e.g., (Ma et al., 2020)), as there is a lot of variability in course assignments to faculty.
In some works, students’ grades are viewed as a useful feature towards recommending courses that students are expected to perform well (Esteban et al., 2018, Mondal et al., 2020, Morsy and Karypis, 2019, Obeidat et al., 2019, Wong, 2018). For example, Wagner et al. (2022) propose a k-nearest neighbors (KNN) model to find similar students based on their grades in prior courses and recommend courses from the history of neighboring students. Jiang et al. (2019) also propose a goal-based CRS using LSTM networks where their goal is to recommend courses with higher expected grades for a near (\(t\)-th) semester and to take a historically difficult course in a far (\((t+1)\)-th) semester.
Another source of information is course descriptions. Textual data has been considered to compute similarities between courses, extract the topics they cover, and build different content-based filtering methods. A hybrid approach combining a force brute search and a Genetic Algorithm has been proposed to find the similarity of courses based on different features including course contents (Esteban et al., 2018). Term Frequency–Inverse Document Frequency (TF–IDF) has been proposed to recommend similar courses using the course description data in Pardos and Jiang (2020) and Naren et al. (2020). Morsomme and Alferez (2019) introduce a topic model (Latent Dirichlet Allocation), use Gibbs sampling algorithm to fit the topic model on course description data, and combine it with a grade prediction model built on student enrollment data to develop a CRS. A statistical confidence-based algorithm is used in a generic conformer CRS utilizing topic modeling to recommend courses based on students’ similarity and courses’ similarity (Warnes and Smirnov, 2020).
3.2. CRS using Course Enrollment Data
Several different CRS have been proposed that utilize only students’ course enrollment data to recommend university courses. Since we are also using this type of data, we will now further delve into these works.
One group of prior works tries to uncover the association of courses taken without considering their timing and the sequential nature of course selection. Bendakir and Aïmeur (2006) explore association rule mining (ARM) and further improve recommendations based on students’ ratings, while Al-Badarenah and Alsakran (2016) cluster the students first and then use ARM in each cluster. The recommended courses are selected from the consequent parts of the rules that are (at least partially) activated by a student’s enrollment history. We can also find several collaborative filtering approaches based on matrix or tensor factorization in the literature. Symeonidis and Malakoudis (2019) build a binary matrix \(\mathbf {B} \in \mathbb {R}^{n\times m}\) with student-course interactions, where \(\mathbf {B}_{u,p}=1\) if student \(u\) has taken course \(p\), i.e., \(p \in H_u\), otherwise \(\mathbf {B}_{u,p}=0\), and use matrix factorization (MF) to approximate \(\hat {\mathbf {B}}_{u,q}\). The courses that \(u\) has not taken before with the highest values of \(\hat {\mathbf {B}}_{u,q}\) are recommended to the student. Tensor factorization (TF) has also been proposed by Zhu et al. (2020) but while using additional information (i.e., teaching evaluations).
Some researchers analyze the sequential nature of courses taken over semesters (which courses are taken in consecutive semesters and/or their long-term dependencies) to recommend courses using matrix factorization (MF), artificial neural networks (ANN), and Markov chain (MC) models to capture this notion. Morsy and Karypis (2019) propose an MF model using singular value decomposition (SVD) to capture sequential transitions of courses. They build a frequency matrix where \(\mathbf {F}_{p,q}\) captures how many times course \(q\) is taken at any semester after course \(p\). After normalizing it row-wise, SVD is applied, and, combined with a grade prediction model, the method recommends subsequent courses with higher expected grades. Pardos et al. (2019) propose a skip-gram model (Course2vec) to predict equivalent (similar) courses and a long short-term memory (LSTM) networks model to recommend courses balancing explicit and implicit preferences of students. Course2vec is a similarity-based approach that recommends courses by computing their cosine similarity with students’ courses taken in the prior semester. All the courses taken by a student are considered as one sentence and each course as a word. For each course, a vector representation is computed to help predict the surrounding courses in a sentence. LSTM networks can learn the long-term and short-term sequential dependencies of courses over the semesters. A bidirectional transformer-based neural networks approach, PLANBERT, has also been introduced to recommend multiple consecutive semesters’ courses toward degree completion of a student (Shao et al., 2021). Reference courses from future semesters are randomly selected, and a Bidirectional Encoder Representations from Transformers (BERT) model is pre-trained and then fine-tuned to recommend courses for the remaining semesters and provide a degree plan to each student. A Markov chain-based model (SkipMarkov) is also introduced for course recommendation (Khorasani et al., 2016). Polyzou et al. (2019) present random walks over Markov chains, Scholars Walk, to capture sequential transitions in consecutive semesters. They perform a random walk with restarts that allows them to consider direct and transitive relations between courses.
The comparison of these approaches in terms of concepts that they capture is presented in Table 2. No prior study captures both the relationship between the co-taken courses and the sequential transitions of courses over semesters together. Our approach fills that gap by considering each semester as a session to recommend correlated and suitable courses for the next semester.
| Type | Model | co-taken courses | course sequence | course similarity | students’ similarity |
course popularity | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Similarity | Course2vec* | ✓ | ✓ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
All these models learn the students’ preferences by inspecting student-course historical interactions. * indicates a model that is implemented and tested in this paper. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Association | ARM* | ✓ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
MF | PlainMFsim* | ✓ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SVD* | ✓ | ✓ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
MC | SkipMarkov | ✓ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ScholarsWalk | ✓ | ✓ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ANN | PlainNN | ✓ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| LSTM | ✓ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PLANBERT | ✓ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.3. Session-based Recommendation systems
In commercial recommender systems, there are different types of session-based recommendation systems to recommend the next clicked item (next interaction), the next partial session (subsequent part) in the current session, or the next basket or complete session with respect to the previous sessions for a user (Wang et al., 2021, Shao et al., 2023). For example, Chen et al. (2023) introduce a knowledge-enhanced multi-view graph neural network model that also captures side information about users, items, and sessions to recommend the next items to partially complete the current session. For our problem setting, the next basket recommendation is the most appropriate and we will focus on approaches that are most relevant to our case.
Rendle et al. (2010) introduce the first next basket recommendation system by presenting a factorized personalized Markov chain (FPMC) model that can capture the first-order dependency of items. Long short-term dependency of items over the sequence of baskets can also be captured by recurrent neural networks. Yu et al. (2016) propose a dynamic recurrent basket model (DREAM) using LSTM networks. Le et al. (2019) propose a correlation-sensitive next basket recommendation model named Beacon to recommend correlated items. MF has been used to recommend the next item or the next basket capturing users’ preferences of choosing one item over another item (Rendle et al., 2014, Guo et al., 2019). Wan et al. (2018) propose a representation learning model, Triple2vec, to recommend complementary and compatible items for the next basket by creating (user, item, item) triples. A TF technique (RESCAL decomposition) has also been proposed to recommend complementary items to a user by creating similar triples (Entezari et al., 2021) and that model outperforms the Triple2vec model for grocery datasets.
In this paper, we explore session-based recommendation approaches to recommend a set of synergistic courses for the next semester. Moreover, note that course enrollment is different from transaction data; a course is most likely to appear once in a sequence of semesters for a student, while in other contexts, one item can appear multiple times (repeated) in different sessions of a user. Some approaches capture repeating items, multiple behaviors (e.g., users’ purchasing, clicking), etc. (Hu et al., 2020, Ariannezhad et al., 2022, Shen et al., 2022). From the plethora of session-based recommendation approaches, we explore the models that are meaningful for our context and data, so we do not use the models that are built focusing on the item re-purchasing and clicking behavior of a user.
4. Session-based course recommendation
While some courses might be worth equal credit hours, the required working time load for each of them can vary based on the difficulty of subjects (Chockkalingam et al., 2021). Students’ course load can impact their performance (Boumi and Vela, 2021). A good combination of courses can balance the workload required within the semester. A set of courses can also be compatible based on factors like concepts or topics covered, the category of each course, required knowledge gained by taking previous courses, etc. The influence of co-taken courses has been considered important for other educational tasks, e.g., grade prediction and early warning systems (Brown et al., 2018, Gardner and Brooks, 2018, Ren et al., 2019).
In this paper, our goal is to capture the synergy among courses taken in the same semester to recommend courses that are well-suited to be studied together. We analyze the relationship and correlation of courses by incorporating the concept of session-based recommendation in course recommendation. We consider a set of courses taken in a semester as a session and inspect the session to understand the relationship among the courses. Let \(\mathcal {B}_{i,t}\) be a set of courses of the \(i\)-th student at semester \(t\). Given the courses for the first \(t_i-1\) semesters for the \(i\)-th student as input, our goal is to recommend a set of correlated courses, \(c_1, c_2..., c_k\) for the target semester \(t_i\) where \(k\) is the number of courses to be recommended and is equal to the number of courses that the student wishes to take in the upcoming semester. We present (1) CourseBEACON and CourseDREAM, two course recommendation models which are based on two popular session-based models (Beacon (Le et al., 2019) and DREAM (Yu et al., 2016), respectively), (2) a tensor-based approach that captures within-session relationships, as well as (3) a post-processing approach that boosts the recommendation scores of correlated courses generated by any CRS.
4.1. CourseBEACON
The framework has three components: correlation-sensitive basket encoder, course basket sequence encoder, and correlation-sensitive score predictor. The architecture of CourseBEACON model is illustrated in Figure 1.
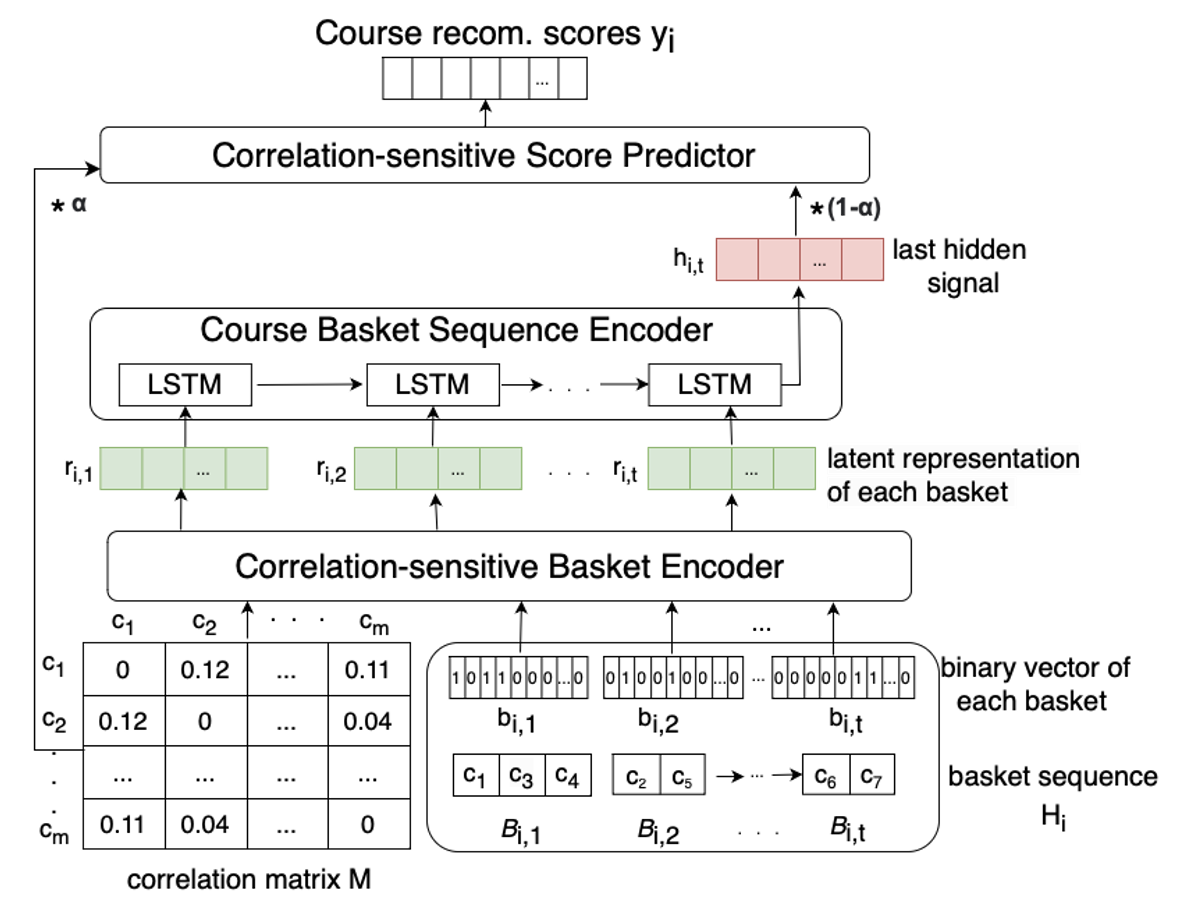
We first need to create the correlation matrix, \(\mathbf {M}\), using all semesters available in training data. Let \(\mathbf {F} \in \mathbb {R}^{m \times m}\) be the frequency matrix. For courses \( p,q \in \mathcal {C}\), \(\forall p \neq q\), \(\mathbf {F}_{p,q}\) is the number of times \(p,q\) co-occur together in a basket (i.e., taken in the same semester). We normalize \(\mathbf {F}\) to generate the final correlation matrix \(\mathbf {M}\) based on the Laplacian matrix \( \mathbf {M} = \mathbf {D}^{-1/2} \mathbf {F} \mathbf {D}^{-1/2},\) where \(\mathbf {D}\) denotes the degree matrix, \(D_{p,p} = \sum _{q \in \mathcal {C}} \mathbf {F}_{p,q}\) (Kipf and Welling, 2017). \(\mathbf {F}\) and \(\mathbf {M} \) are symmetric by definition.
Correlation-Sensitive Basket Encoder For semester \(t\), we create a binary indicator vector, \(\mathbf {b}_{i,t}\) of length \(m\), for the set of courses that were taken by the \(i\)-th student, i.e., the \(j\)-th index is set to \(1\) if \(c_j \in \mathcal {B}_{i,t}\), otherwise, it is set to 0. We get an intermediate basket representation \(\mathbf {z}_{i,t}\) for a basket \(\mathcal {B}_{i,t}\) as follows: \begin {equation} \mathbf {z}_{i,t} = \mathbf {b}_{i,t} \odot \omega + \mathbf {b}_{i,t} * \mathbf {M}, \end {equation} where \(\omega \) is a learnable parameter that indicates the importance of the course basket representation, the circle-dot indicates element-wise product, and the asterisk indicates matrix multiplication. We feed \(\mathbf {z}_{i,t}\) into a fully-connected layer and we get a latent basket representation \(\mathbf {r}_{i,t}\) by applying the ReLU function in an element-wise manner: \begin {equation} \mathbf {r}_{i,t} = ReLU(\mathbf {z}_{i,t} \Phi + \phi ), \end {equation} where \(\Phi \), \(\phi \) are the weight and bias parameters, respectively.
Course Basket Sequence Encoder We use the sequence of latent basket representations \(\mathbf {r}_{i,t}, \forall t\in [1,\dots , t_i-1]\) for the \(i\)-th student as input in the sequence encoder. Each \(\mathbf {r}_{i,t}\) is fed into an LSTM layer, along with the hidden output from the previous layer. We compute the hidden output \(\mathbf {h}_{i,t}\) as: \begin {equation} \mathbf {h}_{i,t} = tanh(\mathbf {r}_{i,t} \Psi + \mathbf {h_{i,(t-1)} \Psi ^\prime + \psi }), \end {equation} where \(\Psi \), \(\Psi ^\prime \) and \(\psi \) are learnable weight and bias parameters.
Correlation-Sensitive Score Predictor We use the correlation matrix and the last hidden output of the last component as the input in the correlation-sensitive score predictor to derive a score for each candidate course. Let \(\mathbf {h}_{i, t_i-1}\) be the last hidden output generated from the sequence encoder. First, we get a sequential signal \(\mathbf {s}_i\) from the given sequence of baskets: \begin {equation} \mathbf {s}_i = \sigma (\mathbf {h}_{i, t_i-1} \mathbf {\Gamma }), \end {equation} where \(\mathbf {\Gamma }\) is a learnable weight matrix parameter and \(\sigma \) is the sigmoid function (i.e., \(\sigma (x) = 1/ (1+ e^{-x})\)). Using the correlation matrix, we get the following predictor vector for the \(i\)-th student of length \(m\): \begin {equation} \mathbf {y}_i = \alpha (\mathbf {s}_i \odot \omega + \mathbf {s}_i * \mathbf {M}) + (1- \alpha ) \mathbf {s}_i, \end {equation} where \(\alpha \in [0,1]\) is a learnable parameter used to control the balance between intra-basket correlative and inter-basket sequential associations of courses. The \(j\)-th element of \(\mathbf {y}_{i}\) indicates the recommendation score of course \(c_j\) to be in the target basket of \(i\)-th student.
4.2. CourseDREAM
We propose the Course Dynamic Recurrent Basket Model (CourseDREAM), based on DREAM, to recommend a set of courses for the target semester. This model has four components: Course-in-a-basket encoder, Pooling layer, Course basket sequence encoder, and the score predictor. The third component is similar to the Course basket sequence encoder of the CourseBEACON model. However, here, we do not explicitly utilize the correlation matrix. Instead, we use a course-in-a-basket encoder to create a latent representation of each course taken in a semester by a student. Then we incorporate max or average pooling, to create one latent representation for each semester a student took classes. After that, we use LSTM networks to create a dynamic representation of a student that captures the dynamic interests of that student throughout his/her study. We recommend the courses with the highest scores for the target semester. The architecture of the CourseDREAM model is depicted in Figure 2.
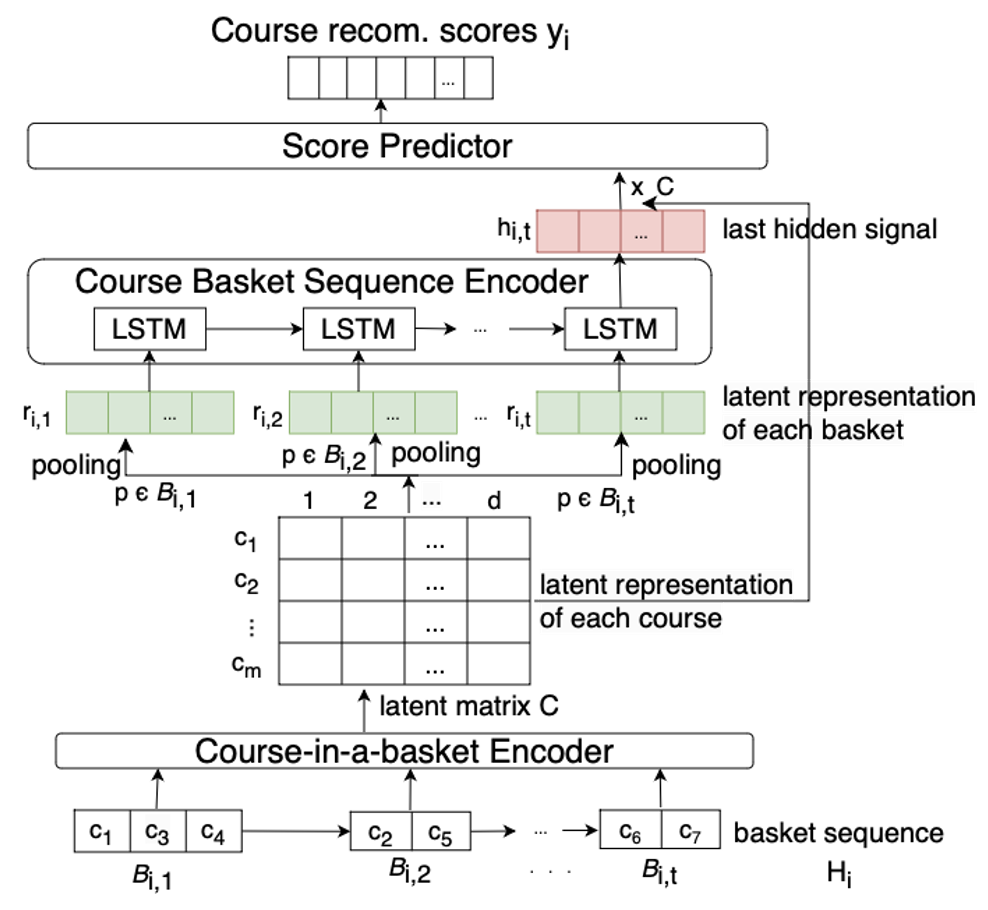
Course-in-a-basket Encoder Each basket of the \(i\)-th student consists of one or more courses. We pass the sequence of baskets of each student to the course-in-a-basket encoder to get a latent representation of each course. The \(j\)-th course that \(i\)-th student took at semester \(t\) has the latent representation \(\mathbf {c}_{i,j}\) with \(d\) latent dimensions. In the output of this step, we get a matrix \(\mathbf {C}\) (\(\in \mathbb {R}^{m \times d}\)) where each row consists of the latent representation of a course.
Pooling Layer We use the matrix \(\mathbf {C}\) to create a latent vector representation \(\mathbf {r}_{i,t}\) for the set of courses that the \(i\)-th student took in semester \(t\) by aggregating the vector representations of these courses, \(\mathbf {c}_{i,p}\), for each \(p \in \mathcal {B}_{i,t}\). We use two types of aggregation operations. First, in max pooling, we take the maximum value of every dimension over these vectors. The \(l\)-th element (\(l \in [1,d]\)) of \(\mathbf {r}_{i,t}\) is created as: \begin {equation} \mathbf {r}_{i,t,l} = max_{p \in \mathcal {B}_{i,t}} (\mathbf {c}_{i,p,l}), \end {equation} where \(\mathbf {c}_{i,p,l}\) is the \(l\)-th element of the course representation vector \(\mathbf {c}_{i,p}\) of course \(p\) of \(i\)-th student. Secondly, for the average pooling, we aggregate the courses’ latent representations in semester \(t\) by taking the average value of every dimension, as follows: \begin {equation} \mathbf {r}_{i,t} = \frac {1}{|\mathcal {B}_{i,t}|} \sum _{p \in \mathcal {B}_{i,t}} \mathbf {c}_{i,p}. \end {equation} Next, these representations of the sequence of baskets are passed to the course basket sequence encoder.
Course Basket Sequence Encoder We incorporate LSTM networks in this encoder where the hidden layer \(\mathbf {h}_{i,t}\) is the dynamic representation of \(i\)-th student at semester \(t\). The recurrent connection weight matrix \(\mathbf {W} \in \mathbb {R}^{d \times d}\) is helpful to propagate sequential signals between two adjacent hidden states \(\mathbf {h}_{i,t-1}\) and \(\mathbf {h}_{i,t}\). We have a learnable transition matrix \(\mathbf {T} \in \mathbb {R}^{t_m \times d}\) between the latent representation of basket \(\mathbf {r}_{i,t}\) and a student’s interests, where \(t_m\) is the maximum length of the sequence of baskets for any student. We compute the vector representation of the hidden layer as follows: \begin {equation} \mathbf {h}_{i,t} = \sigma (\mathbf {T}\mathbf {r}_{i,t} + \mathbf {W} \mathbf {h}_{i,t-1}), \end {equation} where \(\mathbf {h}_{i,t-1}\) is the dynamic representation of the previous semester. \(\sigma (\cdot )\) is the sigmoid activation function.
Score Predictor The model generates a score \(\mathbf {y}_{i, t_i}\) for all available courses that the \(i\)-th student might take at target semester \(t_i\) by using the matrix \(\mathbf {C}\) with the latent representation of all courses and the dynamic representation of the student \(\mathbf {h}_{i,t}\) as follows: \begin {equation} \mathbf {y}_{i,t_i} = \mathbf {C}^T \mathbf {h}_{i,t}, \end {equation} where the \(j\)-th element of \(\mathbf {y}_{i,t_i}\), represents the recommendation score for the \(j\)-th course.
4.3. TF-CoC: session-based method with tensors
We also explore two ways to consider the co-taken courses. First, TF-CoC is a tensor factorization approach that captures the co-taken courses by students but not the sequential transition of the courses. A (students)\(\times \)(courses)\(\times \)(courses) binary tensor is built, \(\mathbf {F} \in \mathbb {R}^{n\times m\times m}\), where \(\mathbf {F}_{i,p,q}=1\) if courses \(p\), \(q\) are taken together in the same semester by the \(i\)-th student. Then we use the RESCAL tensor decomposition technique with factorization rank \(d\) to get the approximate value of \( \mathbf {F}_{i,p,q} \) for any pair of (\(p\), \(q\)) courses. First, we calculate the matrix \(\mathbf {A}\) (course embedding, \( \mathbf {A} \in \mathbb {R}^{m \times d}\)) and tensor \(\mathbf {R}\) (user embedding, \(\mathbf {R} \in \mathbb {R}^{d \times d \times n} \)). Then, we calculate \( \tilde {\mathbf {F}}_{i,p,q} = \mathbf {Q}_p * \mathbf {A}_q^T\) where \( \mathbf {Q}_p \) is the query vector, i.e., the dot product of \( \mathbf {A}_p \in \mathbb {R}^{1 \times d}\) for course \(p\) and \( \mathbf {R}_i \in \mathbb {R}^{d \times d \times 1} \) for \(i\)-th student and \(\mathbf {A}_q^T\) is the transpose of \(\mathbf {A}_q\). Then the course \(q\) is recommended to \(i\)-th student if \(\tilde {\mathbf {F}}_{i,p,q}\) score becomes maximum or average of \(\tilde {\mathbf {F}}_{i,p,q}\) becomes highest where \(p\) represents the courses that are already taken in the prior semester by that student. To speed up the recommendation process, we implement a hashing technique using the approximate nearest neighbor (ApNN) indexing library, ANNOY (Bernhardsson, 2023). In this case, the query vector, \( \mathbf {Q}_p \), is calculated for any course \(p\) taken by \(i\)-th student and we find the courses \(q\) which are nearest neighbors to the query vector using annoy indexing and calculate \(\tilde {\mathbf {F}}_{i,p,q}\).
For recommending courses to new students in validation and test sets, we use a multiple training process, building a new model for each semester that we generate a recommendation for, where we merge the target student’s prior history with the training set, as described in Guo et al. (2019). We have explored different values of factorization rank, \(d\) = [1, 2, 3, 4, 5, 8, 10, 20, 50, 100], and different numbers of nearest neighbors [5, 40, 100] for ApNN indexing. However, we observe better results when we do not use ApNN indexing which takes the maximum number of nearest neighbors (all available courses) into consideration.
4.4. CorA: a post-processing step for CRS
We also consider a post-processing step that could be applied to the recommendation scores of any CRS. The idea is to boost the weights (recommendation scores) of courses that are more likely to be taken together, as follows:
\begin {equation} \mathbf {y}'_i = \mathbf {y}_i + \beta S(\mathbf {y}_i, \gamma ) \mathbf {M}, \end {equation} where \(\beta >0\) is the importance of correlation adjustment and \(S(\cdot )\) is a function that will be set to zero for the scores of the bottom \((m-\gamma )\) courses. In order words we will only boost the weights of the correlated courses of the top \(\gamma \) courses. We denote this model as (base)+CorA, where (base) can be any course recommendation model.
5. Experimental Evaluation
5.1. Dataset
We used a real-world dataset from Florida International University, a public university in the US, that spans nearly nine years. Our dataset consists of the course registration history of undergraduate students in the Computer Science department. The grades follow the A–F grading scale (A, A-, B+, B, B-, C+, C, D, F). We only consider the data of students who have successfully graduated with a degree. We remove instances in which a grade less than C was earned because these do not (usually) count towards degree requirements (Morsy and Karypis, 2019). We also remove an instance if a student drops a class in the middle of the semester. In this way, we keep course sequences and information that at least lead to successful graduation and may be considered good examples. We remove courses that appear less than three times in our dataset. After preprocessing, we have the course registration history of \(3328\) students and there are \(647\) unique courses. We split the data into train, validation, and test sets. We use the last three semesters (summer 2021, fall 2021, and spring 2022) for testing purposes and the previous 3 semesters (summer 2020, fall 2020, and spring 2021) for validation and model selection. The rest of the data before the summer 2020 term (almost seven years’ course registration history) are kept in the training set.
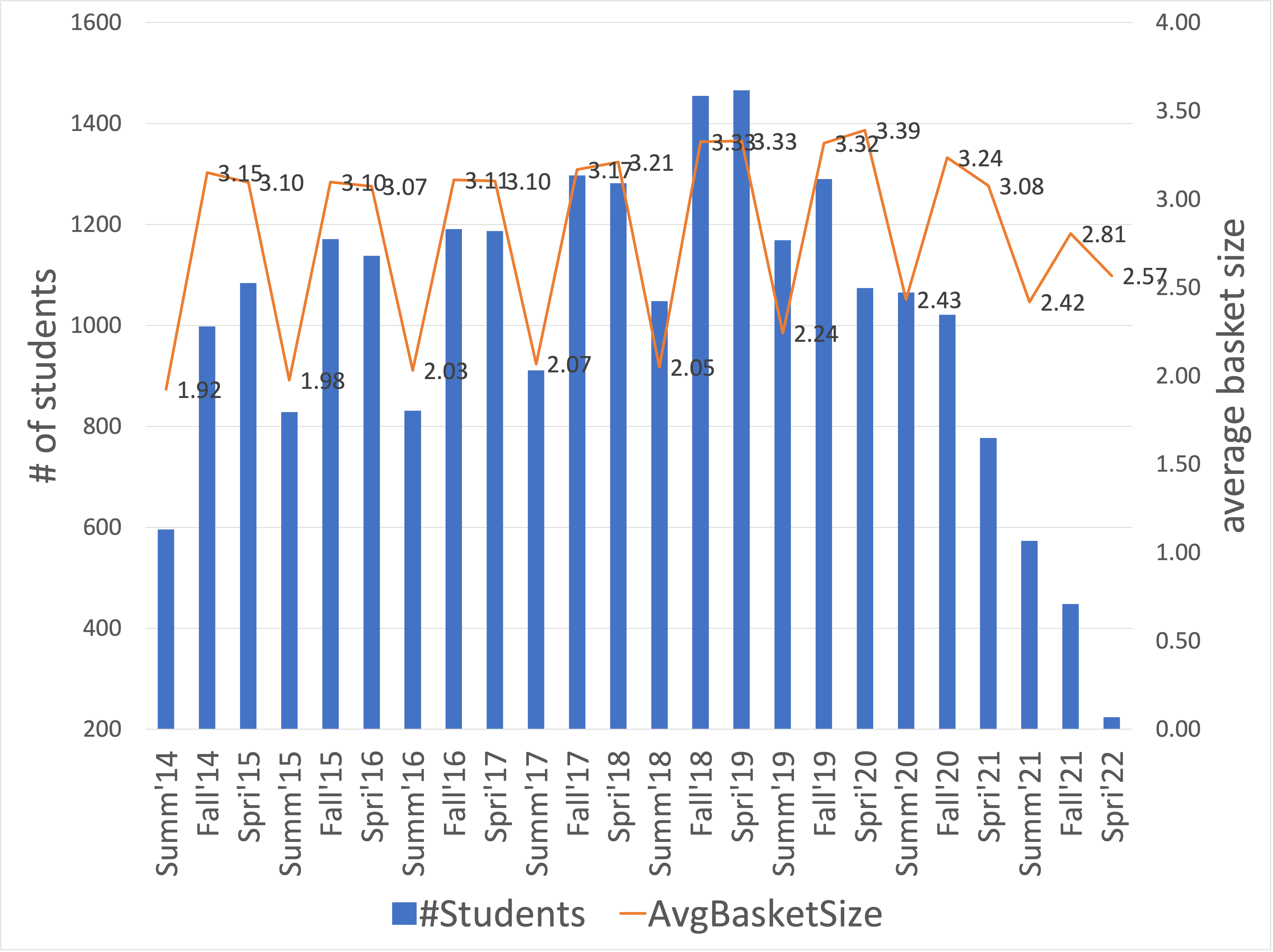
From the validation and test sets, we remove the courses that do not appear in the training set. We also remove any instances from the training, validation, and test set where the length of the basket sequence is less than three for a student. At the very least, we need one target semester and two prior semesters of students’ registration history to have enough input data for our recommendation task. The statistics of training, validation, and test data are presented in Table 3. Each student might correspond to multiple instances, one for each semester that could be considered as a target semester. For example, if a student took courses from fall 2019 until fall 2021, they are considered in two instances on the test set (we generate recommendations for summer 2021 and fall 2021) and with three recommendations in the validation set (target semesters: summer 2020, fall 2020, and spring 2021). The number of students who took courses in each semester and the average basket size of each semester in the training, validation, and test set are presented in Figure 3. While we cannot publicly share our student data, the code for all the methods can be found here: https://github.com/PolyDataLab/SessionBasedCourseRecommendation.
| # students | # courses | # target baskets | |
|---|---|---|---|
| Training | 2973 | 618 | 14070 |
| Validation | 1231 | 540 | 2743 |
| Test | 657 | 494 | 1259 |
5.2. Evaluation metrics
As in prior work (Le et al., 2019, Pardos et al., 2019, Polyzou et al., 2019, Yu et al., 2016), we have used Recall@\(k\) score as our main evaluation metric, where \(k\) is the number of courses that the student took at the target semester. \begin {equation} \text {Recall@}k = \frac { \text {\# of relevant recommendations}}{\text {\# of actual courses in target semester}} \end {equation} We essentially calculate the fraction of courses in the target semester that we correctly recommended to a student. In the subsequent sections, we report the average score over all the recommendations, i.e., target baskets. Recall and precision scores are equal as we recommend as many courses as the target student will take in the target semester. We also calculate the percentage of students for whom we offer at least \(x\) relevant recommendation(s) as follows: \begin {equation} \text {\%$x$+ rel} = \frac { \text {\# instances with $\geq x$ relevant recommendation}}{\text {\# total instances with basket size of at least $x$}} * 100 \end {equation} where \(x\) is the number of correctly recommended courses and basket size is the number of courses in a target semester. This metric captures the ability of our recommendations to retrieve at least one relevant recommendation (%\(1\)+ rel) and at least two relevant recommendations (%\(2\)+ rel) for each student.
To measure the suitability and diversity of the set of correctly recommended (relevant) courses, we compute three additional metrics. We measure the Correlation of Relevant Courses, \(\text {CoReC}_i\) score for each instance as follows: \begin {equation} \text {CoReC}_i = \frac {\sum _{j=1}^{|\mathcal {R}_{i,t}|} ({\sum _{l=1, l \neq j}^{|\mathcal {R}_{i,t}|} \mathbf {M}_{j,l})} / {|\mathcal {R}_{i,t}-1|}} {|\mathcal {R}_{i,t}|} \end {equation}
where \(j\), \(l\) are indices for correctly recommended (cor-rec) courses, \(\mathcal {R}_{i,t}\), for the target semester \(t\) to \(i\)-th student, and \(\mathbf {M}_{j,l}\) is the correlation of \(j\)-th and \(l\)-th courses (as described in Section 4.1). In this metric, we take the average correlation value of each pair of cor-rec courses to get \(\text {CoReC}_i\) for each instance. Then, we average it out over the instances for whom we can provide at least 2 relevant recommendations to get \(\text {CoReC}\).
We compute the Popularity of Relevant Courses, \(\text {PopReC}_i\) score for an instance as follows: \begin {equation} \text {PopReC}_i = \frac {\sum _{j=1}^{|\mathcal {R}_{i,t}|} F_{j}} {|\mathcal {R}_{i,t}|} \end {equation} where \(F_{j}\) is the normalized frequency of \(j\)-th correctly recommended course in \(\mathcal {R}_{i,t}\) for the target semester \(t\). We calculate \(F_{j}\) by counting how many times a course is taken by all the students in the training set and dividing it by the maximum frequency of a course. Then we calculate the average of \(\text {PopReC}_i\) for all instances with at least \(1\) relevant recommendations.
We calculate the coverage of relevant recommendations that compute how many unique courses we can recommend correctly over all the testing instances. The formula is as follows: \begin {equation} \text {coverage} = \frac { \text {\# of correctly recommended unique courses}}{\text {total unique courses in the test set}} \end {equation} This metric provides the notion of diversity of the recommendations by each model.
5.3. Experimental setting
We use the training set to build the models, and we select the parameters with the best performance on the validation set based on the Recall@\(k\) metric. For the model selected, we calculate the evaluation metrics on the test set.
For the CourseBEACON model, for parameter \(\alpha \), we have tested the values [0.1, 0.3, 0.5, 0.7, 0.9]. The parameter \(\alpha \) balances the importance of intra-basket correlation and inter-basket sequential association of courses. The lower value of \(\alpha \) prioritizes the sequential association more than the intra-basket correlation; a higher value prioritizes the correlation of courses within the basket more. We also examined embedding dimensions=[16, 32, 64], hidden units=[32, 64, 128] of LSTM networks, and dropout rates=[0.3, 0.4]. For the CourseDREAM model, we used both max pooling and average pooling, however, the outcomes were very similar. In this paper, the results are reported with the average pooling technique. We have explored LSTM layers=[1, 2, 3], embedding dimensions=[8, 16, 32, 64], and dropout rates=[0.3, 0.4, 0.5, 0.6] for the CourseDREAM model. For MF and TF methods, we have explored different values of latent factors, \(d\) = [1, 2, 3, 4, 5, 8, 10, 20, 50, 100].
For CorA, we will use CourseDREAM, SVDcs, Scholars Walk, and LSTM models as the base models. For correlation adjustment, we explore \(\beta =[0.001, 0.01, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6]\) and \(\gamma = [2, 3, 5, 10, 15, 20, 25, m]\).
5.4. Competing approaches
We implement models that use course enrollment data only. Precisely, we re-implement different competing approaches (models in bold, Table 2). We also modify and extend the existing matrix and tensor factorization approaches. The notions captured by these extended models and proposed models are represented in Table 4. For example, the BPRMF model captures students’ similarity by considering similar students’ course-taking behavior.
| Type | Model | students’ similarity | course sequence |
co-taken courses |
|---|---|---|---|---|
|
MF | PlainMF | ✓ | ||
| BPRMF | ✓ | |||
| BPRMFsim | ✓ | |||
| SVDcs | ✓ | |||
|
TF | TF-CoC | ✓ | ✓ | |
| TF-CoCsim | ✓ | ✓ | ||
| TF-CS | ✓ | ✓ | ||
| TF-CSsim | ✓ | ✓ | ||
| TF-APS | ✓ | ✓ | ||
| TF-APSsim | ✓ | ✓ | ||
| TF-SCT | ✓ | |||
| TF-SCTsim | ✓ | |||
|
ANN | CourseBEACON | ✓ | ✓ | |
| CourseDREAM | ✓ | ✓ |
5.4.1. Baselines
We use a popularity-based approach (PopInTerm) as a non-sequential baseline (Elbadrawy and Karypis, 2016). Starting from the first semester of each student, we count how many students take course \( p \in \mathcal {C} \) in that semester of their studies. The top courses with the highest frequency at the \(t\)-th semester are recommended for the \(t\)-th semester of a target student. For example, if we have a student whose target semester is their fourth semester in the program, we will recommend the most popular courses that students (in the training set) take in their fourth semester.
We consider a popularity- and sequence-based approach (PopInSeq). We create a bipartite graph between “before” and “after” courses in a sequence, where the weight of a connecting edge, weight \((p, q)\), increases by 1 for each student taking course \(p\) before course \(q\). We normalize the weights as: \( \text {weight}(p, q) = { \text {weight}(p, q)}/{\sum _{\forall r \in \mathcal {C}} \text {weight}(p, r)}. \) The recommendation score of course \(q\) for the target semester of the \(i\)-th student is computed as: \[ \mathbf {y}_{i,q}=\sum _{p\in \mathcal {B}_{i,t_i-1}}\text {weight}(p, q). \]
5.4.2. Similarity-based and Association-based approaches
Course2vec We re-implement the Course2vec model (similar to Word2vec) described in Pardos et al. (2019) and Pardos and Jiang (2020). For the recommendation score of each course \(p \in \mathcal {C}\), we sum up its cosine similarity scores with all other courses taken in the last semester. We also use all the prior courses of all prior semesters of a student, but using only the last semester performs better. We have explored different vector sizes, [100, 200, 300, 400, 500, 600]. As our vocabulary size is 618 (total number of courses), we didn’t try a vector size of more than 600.
ARM To be consistent in our evaluation, we implement an association rule mining method without considering grade as a feature, so we skip clustering the students based on their grades as it is done in existing approaches (Al-Badarenah and Alsakran, 2016, Obeidat et al., 2019). We implement the Apriori algorithm using scikit-learn (Pedregosa et al., 2011) to generate rules. For recommendation, we use a threshold for the percentage of match courses between the antecedent part and the prior courses of a student (%match) to activate a rule. For each course, we compute its recommendation score by summing up the confidence of any activated rules where the course is available in the consequent part. We also add up the scores of not-matched courses in the antecedent part of activated rules. We have explored confidence thresholds = [\(0.3\), \(0.4\), \(0.5\), \(0.6\)] and support thresholds = [\(0.10\), \(0.15\), \(0.20\), \(0.25\)] to generate rules and different threshold values for %match = [\(40\), \(50\), \(60\), \(70\)] to activate rules for recommendation.
5.4.3. Matrix Factorization (MF) approaches
PlainMF We use the matrix factorization model with an alternating least square optimization technique (Hu et al., 2008, Malhotra et al., 2022). Matrix factorization reconstructs the user-item interactions matrix (size \(n \times m\)) and estimates recommendation scores for unknown items for each user. It builds a user embedding and an item embedding, \(\mathbf {e}_u \in \mathbb {R}^{1\times d}\) for each student \(u\) and a vector \(\mathbf {f}_p \in \mathbb {R}^{1\times d}\) for each course \(p\), where \(d\) is the factorization rank. We calculate the approximate value of a student selecting a course as \(\mathbf {e}_u\mathbf {f}^T_p\). For recommendation, target students need to have their latent vector representation \(\mathbf {e}_u\) built during model training, so we use a multiple training process described in Subsection 4.3.
BPRMF We also implement the matrix factorization model with a different optimization technique, i.e., Bayesian personalized ranking (BPRMF) (Rendle et al., 2014). Using the training data, we construct an \(m \times m\) matrix \(\mathbf {P}_u\) for each student \(u\), ranking course \(p\) over course \(q\), where \(p\) is any course taken by \(u\) at any semester and \(q\) is any course not taken by \(u\). We estimate the probability of ranking course \(p\) over course \(q\) for student \(u\), denoted as \(prob (u, p, q)\). For recommendation, the score of any course \(p\) is calculated by the summation of the probabilities of \((u, p, q)\) where \(\forall q \in \mathcal {C}, q \neq p \) for student \(u\).
PlainMFsim and BPRMFsim Instead of the multiple training process, we can also generate recommendations for unseen users by finding and using similar students’ representations in the trained model. For each student, we create a binary vector of size \(m\), where we put 1 if a course \(p\) is taken by that student at any prior semester. We use cosine similarity to find similar students. Then, we average out the recommendation scores for all the courses from all similar students \(\hat {b}_{u,p}\) (\(u\) is the similar user of an unseen user) and recommend the set of courses with the highest scores. In this paper, we implement the same PlainMF and BPRMF models described above with the cosine similarity-based recommendation process. We denote these models as PlainMFsim and BPRMFsim. We have explored the number of similar students = [3, 5, 10].
SVD We implement the singular value decomposition model similar to Morsy and Karypis (2019), however, we do not consider grades of courses. Instead, we build the frequency matrix, \(\mathbf {F} \in \mathbb {R}^{m\times m}\) by counting if a course \(p\) is taken before \(q\) at any prior semester. We implement SVD on the normalized frequency matrix using the SciPy library (Virtanen et al., 2020) and get three matrices: \(\mathbf {U} \in \mathbb {R}^{m\times d}\), \(\mathbf {\Sigma } \in \mathbb {R}^{d\times d}\), and \(\mathbf {V} \in \mathbb {R}^{d\times m}\), where \(d\) is the number of singular values. Then, we use \(\mathbf {U}\sqrt {\mathbf {\Sigma }}\) and \(\mathbf {V}\sqrt {\mathbf {\Sigma }}\) as the latent representation of all prior courses and of subsequent courses, respectively. For recommendation, we calculate the average over the course embeddings of prior courses taken by each student in all prior semesters, resulting in a latent representation of student preferences in prior semesters. By multiplying this with the latent representation of candidate courses (\(\mathbf {V}\sqrt {\mathbf {\Sigma }}\) matrix), we get the recommendation scores. We also explore a truncated SVD model with a different number of singular values \(d\)= [\(16\), \(32\), \(64\), \(128\), \(256\), \(512\), \(617\), \(m\)], where the regular SVD model has \(d=m (=618)\). We get better results with a truncated SVD model as Morsy and Karypis (2019).
SVDcs We implement the SVD model described above using a different frequency matrix here. We count how many times a course is taken after a course only in consecutive semesters (cs), without skipping any semester. We implement regular SVD and truncated SVD (as described above) on the normalized frequency matrix and use the same recommendation process.
5.4.4. Tensor Factorization (TF)
Since we explore a TF approach for session-based course recommendation, we will also compare other ways to construct a tensor that does not capture the session notion. A summary of the tested approaches is shown in Table 5.
TF-CS We implement a tensor decomposition similar to Entezari et al. (2021) and TF-CoC, but using a different tensor. Now, the elements of the tensor \(\mathbf {F} \in \mathbb {R}^{n\times m\times m}\), \(\mathbf {F}_{i,p,q}\), store the number of times that course \(p\) is taken before \(q\) in consecutive semesters by the \(i\)-th student. We denote this model as TF-CS where CS indicates courses that are taken sequentially in consecutive semesters. For evaluation, for the \(i\)-th student, we compute the recommendation score of course \(q\) by taking the maximum value or summation of \(\tilde {\mathbf {F}}_{i,p,q}, \forall p \in B_{i,(t_i-1)}\). We build a new model for each semester we need to generate a recommendation.
TF-APS In this tensor decomposition approach, we do not consider the notion of a session. We create the tensor \(\mathbf {F} \in \mathbb {R}^{n\times m\times m}\), where \(\mathbf {F}_{i,p,q}=1\) if \(p\) is taken before \(q\), where \(p\) is any course taken in any prior semesters, and \(q\) is any course taken in target semester by the \(i\)-th student. We denote this model as TF-APS where APS indicates prior courses of all prior semesters. For the recommendation score for each course \(q\), we sum up the \(\tilde {\mathbf {F}}_{i,p,q}\) scores for all courses \(p\) that the student took in all prior semesters.
TF-SCT This time, we create a tensor \(\mathbf {F} \in \mathbb {R}^{n\times m\times s}\), where \(\mathbf {F}_{i,p,t} = 1\) if course \(p\) is taken by the \(i\)-th student at \(t\)-th semester, and \(s\) is the maximum number of semesters any student took courses. We recommend the courses \(p\) that have the highest \(\tilde {\mathbf {F}}_{i,p,t_i}\) scores. We denote this model as TF-SCT where SCT indicates (student-course-term) triple.
| Model | Non-zero entries for \(i\)-th student | Tensor dimensions | Score of course q, \(\mathbf {y}_{i,t_i,q}=\) |
|---|---|---|---|
| TF-CoC | \(\mathbf {F}_{i,p,q}\), if \(p\),\(q\) courses are co-taken in a semester | \(\mathbb {R}^{n\times m\times m}\) | \(\tilde {\mathbf {F}}_{i,p,q}\), for any course \(p \in \mathbf {H}_i\) taken in prior terms |
| TF-CS | \(\mathbf {F}_{i,p,q}\), if \(p\) is taken before \(q\) in cons. semesters | \(\mathbb {R}^{n\times m\times m}\) | \(\sum _{\forall p \in \mathcal {B}_{i,(t_i-1)}} \tilde {\mathbf {F}}_{i,p,q}\), over courses in the previous term |
| TF-APS | \(\mathbf {F}_{i,p,q}\), if \(p\) is taken any time before \(q\) of target term | \(\mathbb {R}^{n\times m\times m}\) | \(\sum _{\forall p \in \mathbf {H}_i} \tilde {\mathbf {F}}_{i,p,q}\), over courses in prior terms |
| TF-SCT | \(\mathbf {F}_{i,p,t}\), if course \(p\) is taken at \(t\)-th semester | \(\mathbb {R}^{n\times m\times s}\) | \(\tilde {\mathbf {F}}_{i,q,t_i}\) for target semester \(t_i\) |
TF-CoCsim, TF-CSsim, TF-APSsim, and TF-SCTsim Similarly to the MF models, we also examine the similarity-based recommendation process for the TF approaches. For each student that does not have a user representation, we use the cosine similarity measure to find the similar students’ representations and utilize them to get recommendation scores for each course. We have also explored the number of similar students = [\(3\), \(5\), \(10\)] for these approaches.
5.4.5. Markov chain-based approaches
Scholars walk We re-implement the Scholars walk model (Polyzou et al., 2019). First, we calculate matrix \(\mathbf {F} \in \mathbb {R}^{m \times m} \) that contains the frequency \(\mathbf {F}_{p,q}\) of every pair of consecutive courses \( p,q \in \mathcal {C} \). We normalize \(\mathbf {F}\) to get the transition probability matrix, \(\mathbf {T}\). Then we perform a random walk on the course-to-course graph that is described by \(\mathbf {T}\). We have explored the following values for the parameters: the number of steps allowed=[1,2,3,4,5]; \(alpha\)=[1e-4, 1e-3, 1e-2, 1e-1, 0.2, 0.4, 0.6, 0.7, 0.8, 0.85, 0.9, 0.99, 0.999]; \(beta\) values from 0 to 1.6 with step 0.1.
5.4.6. Neural network-based approaches
PlainNN We train a neural network model similar to the LSTM-based model as in Pardos et al. (2019) and the course2vec model described in Morsy and Karypis (2019). In this model, we build a plain neural network using one or more hidden layers and a fully connected layer. We create a list of all prior courses of all prior semesters maintaining the sequence of courses based on timestamps of semesters. As there is no sequence in courses within a semester, courses are randomly shuffled within a semester and we use the courses of last semester as the target semester \(\mathcal {B}_{i,t}\) for student \(i\). As input, we feed a multi-hot encoding representation of the created list of courses to the neural network architecture. In our model, we have explored the number of hidden layers = [1, 2, 3], the number of hidden units in a hidden layer = [32, 64, 128, 256], and the dropout rate = [0.3, 0.4].
LSTM We re-implement the LSTM-based course recommendation model described in Pardos et al. (2019) and Jiang and Pardos (2020). We create a multi-hot representation of courses per timestamp (semester) for each student to be used as input and feed the sequence of semesters’ representations to the LSTM architecture. Then, we use a sigmoid activation function to convert the last hidden signal into a probability distribution of all available courses to be predicted in the target semester. We have explored the number of hidden layers = [1, 2, 3], the number of hidden units in a hidden layer = [32, 64, 128, 256], and the dropout rate = [0.3, 0.4].
PLANBERT We re-implement the PLANBERT model proposed in Shao et al. (2021) and adapt it to recommend only courses in the next semester. To be consistent with the rest of our experiments, we do not use any future reference course, only the student-course interactions. From the course history \(H_i\) of \(i\)-th student, we make one sentence with all the prior courses taken before the target semester. Then, we utilize the pre-trained DistilBERT model from Hugging Face1 which is similar to the BERT model used in the PLANBERT model. We use the data collator for Language Modeling2 to prepare the tokenized words with some masked tokens where \(\alpha \) = [15, 20, 25] percent tokens (randomly chosen) are masked in each batch of data. Then we fine-tune the model with all the batches created from training data where the masked tokens are the tokens to be predicted. To recommend, we create one sentence by using the prior courses of each student and add a mask token at the end of each sentence to predict the next word which would be the next course for the next semester. Then the courses with the higher scores are predicted as the next word of the sentence.
5.5. Filtering and recommending courses
We recommend the top courses for the target semester \(\mathcal {B}_{i, t_i}\) based on the predicted score for course \(c_j\) for \(i\)-th student. During post-processing, while recommending courses for a student, we filter out the courses that the student took in any previous semester and the courses that are not offered at that target semester (Pardos et al., 2019, Polyzou et al., 2019). Then, we recommend the top \(k = |\mathcal {B}_{i, t_i}|\) courses.
6. Results
In this section, we will discuss the performance of our proposed approaches (3 main approaches, CourseBEACON, CourseDREAM, TF-CoC, and 4 approaches with the CorA post-processing step) compared to 9 existing competing approaches, along with 11 additional approaches we explore in this paper. We will evaluate the characteristics of the set of recommended courses provided by each model. We will also present how the hyperparameters affected the overall performance of our models.
6.1. Overall Recommendation Performance Comparison
The performance results across different models are shown in Table 6, where we present the Recall@\(k\) scores for both validation and test sets and %\(1\)+ rel and %\(2\)+ rel scores for the test data.
|
Type/Focus |
Model | Recall@\(k\) |
%1+ rel |
%2+ rel | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
* indicates a model we propose or extend from existing approaches. For each metric, the best-performing scores are in bold font, and the second- and third-best scores are underlined. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Validation | Test | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Popularity | PopInTerm | 0.160 | 0.104 | 26.21 | 5.36 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PopInSeq | 0.299 | 0.247 | 49.96 | 20.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Similarity | Course2vec | 0.177 | 0.157 | 35.50 | 13.84 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Association | ARM | 0.358 | 0.292 | 56.31 | 23.49 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
MF | PlainMF* | 0.354 | 0.293 | 56.95 | 24.85 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PlainMFsim | 0.362 | 0.288 | 56.31 | 24.76 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BPRMF* | 0.337 | 0.278 | 54.33 | 23.39 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BPRMFsim* | 0.357 | 0.293 | 56.79 | 24.95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SVD | 0.331 | 0.253 | 51.87 | 20.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SVDcs* | 0.405 | 0.296 | 56.79 | 24.37 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SVDcs+corA* | 0.408 | 0.298 | 57.19 | 24.56 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TF | TF-CoC* | 0.294 | 0.233 | 46.54 | 20.18 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TF-CoCsim* | 0.322 | 0.253 | 50.36 | 21.73 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TF-CS* | 0.349 | 0.291 | 56.71 | 24.56 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TF-CSsim* | 0.360 | 0.282 | 55.44 | 23.29 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TF-APS* | 0.329 | 0.256 | 51.87 | 20.76 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TF-APSsim* | 0.328 | 0.271 | 55.04 | 21.54 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TF-SCT* | 0.223 | 0.229 | 48.77 | 15.79 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TF-SCTsim* | 0.098 | 0.083 | 17.95 | 3.31 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
MC | ScholarsWalk | 0.362 | 0.268 | 52.42 | 23.68 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ScholarsWalk+corA* | 0.364 | 0.269 | 52.50 | 23.68 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ANN | PlainNN | 0.263 | 0.201 | 43.91 | 14.92 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| LSTM | 0.313 | 0.261 | 52.58 | 21.17 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| LSTM+corA* | 0.277 | 0.254 | 51.56 | 19.92 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PLANBERT | 0.341 | 0.273 | 55.60 | 22.42 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CourseBEACON* | 0.388 | 0.303 | 58.70 | 25.83 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CourseDREAM* | 0.383 | 0.310 | 59.41 | 26.41 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CourseDREAM+corA* | 0.384 | 0.313 | 59.73 | 26.41 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
First, we compare the results within approaches of the same type. For popularity baselines, we observe that PopInSeq outperforms PopInTerm, which is a first indication that the sequential nature of course enrollment is very important. From the MF approaches, the SVDcs+CorA model outperforms the rest, providing the best validation and test recall scores among them. Among the TF models, the TF-CS model outperforms other TF-based models, which indicates that creating a triple with (student, prior course, next course in consecutive semesters) works better. Out of the ANN approaches, our proposed CourseDREAM+CorA model performs best in terms of test recall, %\(1\)+ rel and %\(2\)+ rel scores.
Second, across all models of different types, we see that our proposed CourseDREAM+CorA model outperforms existing competing approaches providing better validation and the best test recall scores. The CourseDREAM+CorA model is also more stable compared to the CourseBEACON model as we can see less difference in validation and test recall scores. The CourseDREAM+CorA model also provides \(1\)+ relevant recommendations for \(59.73\)% of instances and \(2\)+ relevant recommendations for \(26.41\)% of the instances, outperforming others. We visualize the performance of the top 10 best-performing models (without considering the +CorA methods; we present those separately) in Figure 4 and Figure 5. The best-performing model in these scatter plots will be at the top right side, with high recall and high %1+ (or %2+) rel scores. CourseDREAM outperforms others in providing more relevant recommendations and better recall scores in both scatter plots.
On the other side, except for the PopInTerm popularity baseline, Course2vec performs significantly worse than the other approaches in terms of recall@\(k\) scores. One reason could be that the Course2vec model only recommends courses similar to the prior courses of the last semester taken by a student and these courses might be more relevant to that prior semester, not that much relevant for the next semester.
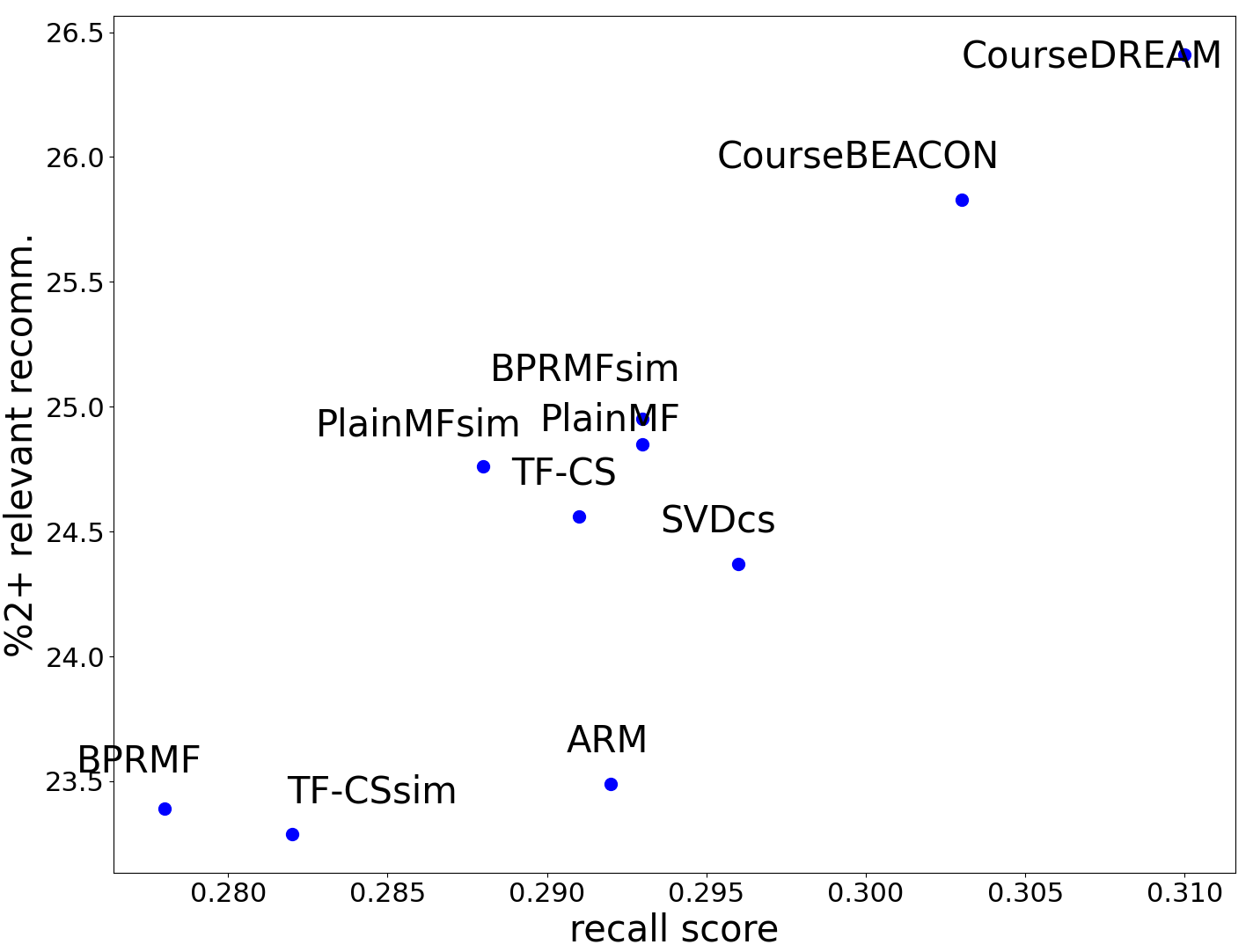
Third, we compare the models with and without the post-processing step added by our proposed +CorA method. The scatter plots of recall@\(k\) and %\(1\)+/%\(2\)+ rel scores for CourseDREAM, SVDcs, ScholarsWalk (SWalk), and LSTM models with and without correlation adjustments for the test data is illustrated in Figure 6 and Figure 7. We observe that we get slightly better performance for the first three models with correlation adjustments than without correlation adjustments. However, for the LSTM model, we observe the opposite with the correlation adjustments. Since the +CorA methods behave similarly to their base models, with a slight performance improvement, for simplicity, we will move forward with the base models.


6.2. Evaluating Suitability of Courses for a Session
Here, we present more insights about our recommendations and measure the suitability of co-recommended courses for the target semester. To better understand the comparison between our best proposed approach (CourseDREAM) and the best-performing competing approach (SVDcs) in providing 0, 1, 2, 3, 4, 5, and 6+ relevant recommendations for the different numbers of courses in a target semester (basket sizes), we present two heat maps in Figure 8 and Figure 9 for these two models for the test data. Here, we use the number of courses in the target semesters (basket size) in the X-axis and the number of relevant recommendations in the Y-axis. The value of each box indicates the total number of instances with (basket size, number of relevant recommendations) pairs in the test set.
The number of instances with no correct recommendation (top row) is fewer using the CourseDREAM than the SVDcs model for the same basket sizes. Additionally, CourseDREAM manages to recommend at least as many relevant courses as SVDcs or more for longer baskets with more courses. We observe similar trends on the corresponding plots comparing CourseDREAM+CorA and SVDcs+CorA, in Figure 10 and Figure 11.
Next, we present the correlation and popularity of correctly co-recommended courses (CoReC and PopReC scores) and coverage of \(10\) best-performing models for the test data in Table 7 (without considering the +CorA methods). First, we observe that our proposed CourseDREAM model recommends the least popular courses compared to other models, providing the lowest PopReC score (0.4113). It indicates that CourseDREAM model can identify less popular courses that are correctly recommended to the target students. This model also provides the lowest CoReC score and the maximum number of baskets. This indicates that CourseDREAM provides at least two relevant recommendations for the maximum number of target instances that have at least two courses and these correctly-identified courses are less correlated. It shows the strength of this model to recommend a better set of courses that are less co-occurred within a semester in the training set, but mostly relevant to the target students. In terms of coverage, the SVDcs model correctly recommends more unique courses (\(11.42\)%). So, the recommended courses from the SVDcs model are more diverse than others, but less accurate than our proposed models.
| Model | PopReC (tot bsize1) | CoReC (tot bsize2) | Coverage |
|---|---|---|---|
| ARM | 0.434 (709) | 0.046 (241) | 0.077 |
| PlainMF | 0.439 (717) | 0.045 (255) | 0.096 |
| PlainMFsim | 0.439 (709) | 0.045 (254) | 0.093 |
| BPRMF | 0.432 (684) | 0.045 (240) | 0.108 |
| BPRMFsim | 0.427 (715) | 0.045 (256) | 0.099 |
| SVDcs | 0.427 (715) | 0.047 (250) | 0.114 |
| TF-CS | 0.420 (714) | 0.047 (252) | 0.108 |
| TF-CSsim | 0.426 (698) | 0.047 (239) | 0.105 |
| CourseBEACON | 0.423 (739) | 0.047 (265) | 0.093 |
| CourseDREAM | 0.411 (748) | 0.044 (271) | 0.102 |


6.3. More Insights and Important Factors of Course Recommendation
Additional insights from our experiments:
- 1.
- Matrix factorization approaches work better than tensor-based ones (potentially because the available data are not enough to train the TF models).
- 2.
- The association rule mining approach, ARM, achieves a relatively high percentage of %1+ rel scores, but these scores drop significantly for the instances with 2+ relevant recommendations.
- 3.
- For both matrix and tensor factorization approaches, the ones that perform the best are those that consider the sequential nature of the data. Among the existing sequential approaches (factorization-based, neural networks, and Markov chain-based) that capture sequential transitions of courses over semesters, PLANBERT performs better, providing a test recall score of 0.273. Our proposed SVDcs model, which is also a sequential approach, outperforms the PLANBERT model providing better validation and test recall scores.
- 4.
- Among other existing and extended non-sequential approaches, the matrix-factorization-based approaches, PlainMF and BPRMFsim perform better than others.
- 5.
- While the performance of the BPRMFsim method (when we do not explicitly create user representations for the target students) is better than BPRMF, we do not observe the same trend for PlainMF.
- 6.
- While Scholars Walk and its +CorA version are on the \(7^{th}\)-\(8^{th}\) position in terms of validation recall, their test performance significantly drops in the test set. This means that Scholars Walk overfits the data and it fails to recommend relevant courses for new students. Alternatively, it is more sensitive than the rest of the models to slight changes in trends in the training and test data.
- 7.
- Between the proposed models, CourseBEACON and CourseDREAM, the latter seems to be more stable, as there is a smaller difference between the validation and test performance.
- 8.
- Deep learning models (like LSTM networks) can capture the sequential transition of courses over the sequence of semesters. Incorporating the notion of the suitability of courses co-taken within a semester produces more accurate and useful recommendation performances.
- 9.
- Overall, our proposed session-based approaches (which also capture the sequential transition of courses) outperform all the other competing approaches for course recommendation that we tested.
6.4. The effect of different hyperparameters
First, we examine how the parameter \(\alpha \) affects the results of the CourseBEACON model. In Figure 12, we present the Recall@\(k\) of the validation and test set achieved for different values of \(\alpha \) for the combination of parameters that have the best Recall@\(k\) (dropout rate = 0.4, embedding dimension \(d=64\), and hidden units = 128). We observe that lower values of \(\alpha \) provide better performance, with the best model having \(\alpha =0.3\). This means that the sequential transition of courses plays more importance than the intra-basket correlation of courses within a semester. However, we still need to consider the relationship between courses taken in the same semester for better recommendations because we get better recall scores when \(\alpha >0\). This is what gives an advantage to these session-based models.
The effect of all hyperparameters tested in the CourseBEACON model is presented in Table 8. Here, we have also set the dropout rate to \(0.4\) which gives us the best-performing model. We observe better recall scores for higher embedding dimensions (emb dim.) (\(32\), \(64\)), higher hidden units (\(64\), \(128\)), and lower values of \(\alpha \) (\(0.1\), \(0.3\)). We also see significant changes in recall scores (very lower) when we set embedding dimensions = \(16\) and hidden units = \(32\) for both validation and test sets.
Next, we examine the performance of the CourseDREAM model with respect to the parameters of embedding dimension and number of RNN layers (LSTM layers) in Table 9. Here, we have set the dropout rate to \(0.4\), which gives us the best-performing model. We observe that the number of LSTM layers and the number of embedding dimensions do influence the results. Except for the case of 8 embedded dimensions, our models benefit from the increased number of RNN layers, which capture more complex patterns in the data. We have selected the model that gives us a better validation recall score, the best test recall score, and a lower difference between validation and test recall scores. The hyperparameters set {embedding dimensions = \(64\), RNN layers = \(3\), dropout rate = \(0.4\)} provides the best model.
|
\(\alpha \) | emb dim. | hidden units = 32 | hidden units = 64 |
hidden units =128 | |||
|---|---|---|---|---|---|---|---|
| Valid Recall | Test Recall | Valid Recall | Test Recall | Valid Recall | Test Recall |
||
| 0.1 | 16 | 0.162 | 0.114 | 0.322 | 0.274 | 0.364 | 0.304 |
| 0.1 | 32 | 0.121 | 0.074 | 0.360 | 0.288 | 0.372 | 0.295 |
| 0.1 | 64 | 0.348 | 0.273 | 0.374 | 0.298 | 0.367 | 0.294 |
| 0.3 | 16 | 0.335 | 0.269 | 0.363 | 0.298 | 0.371 | 0.296 |
| 0.3 | 32 | 0.301 | 0.244 | 0.358 | 0.287 | 0.369 | 0.299 |
| 0.3 | 64 | 0.346 | 0.282 | 0.374 | 0.291 | 0.388 | 0.303 |
| 0.5 | 16 | 0.317 | 0.243 | 0.359 | 0.285 | 0.340 | 0.268 |
| 0.5 | 32 | 0.281 | 0.227 | 0.340 | 0.263 | 0.350 | 0.275 |
| 0.5 | 64 | 0.334 | 0.254 | 0.340 | 0.275 | 0.361 | 0.283 |
| 0.7 | 16 | 0.287 | 0.228 | 0.327 | 0.252 | 0.343 | 0.275 |
| 0.7 | 32 | 0.136 | 0.106 | 0.324 | 0.249 | 0.356 | 0.276 |
| 0.7 | 64 | 0.289 | 0.232 | 0.344 | 0.264 | 0.330 | 0.268 |
| 0.9 | 16 | 0.159 | 0.102 | 0.149 | 0.116 | 0.327 | 0.262 |
| 0.9 | 32 | 0.148 | 0.117 | 0.141 | 0.104 | 0.339 | 0.263 |
| 0.9 | 64 | 0.136 | 0.084 | 0.311 | 0.242 | 0.297 | 0.237 |
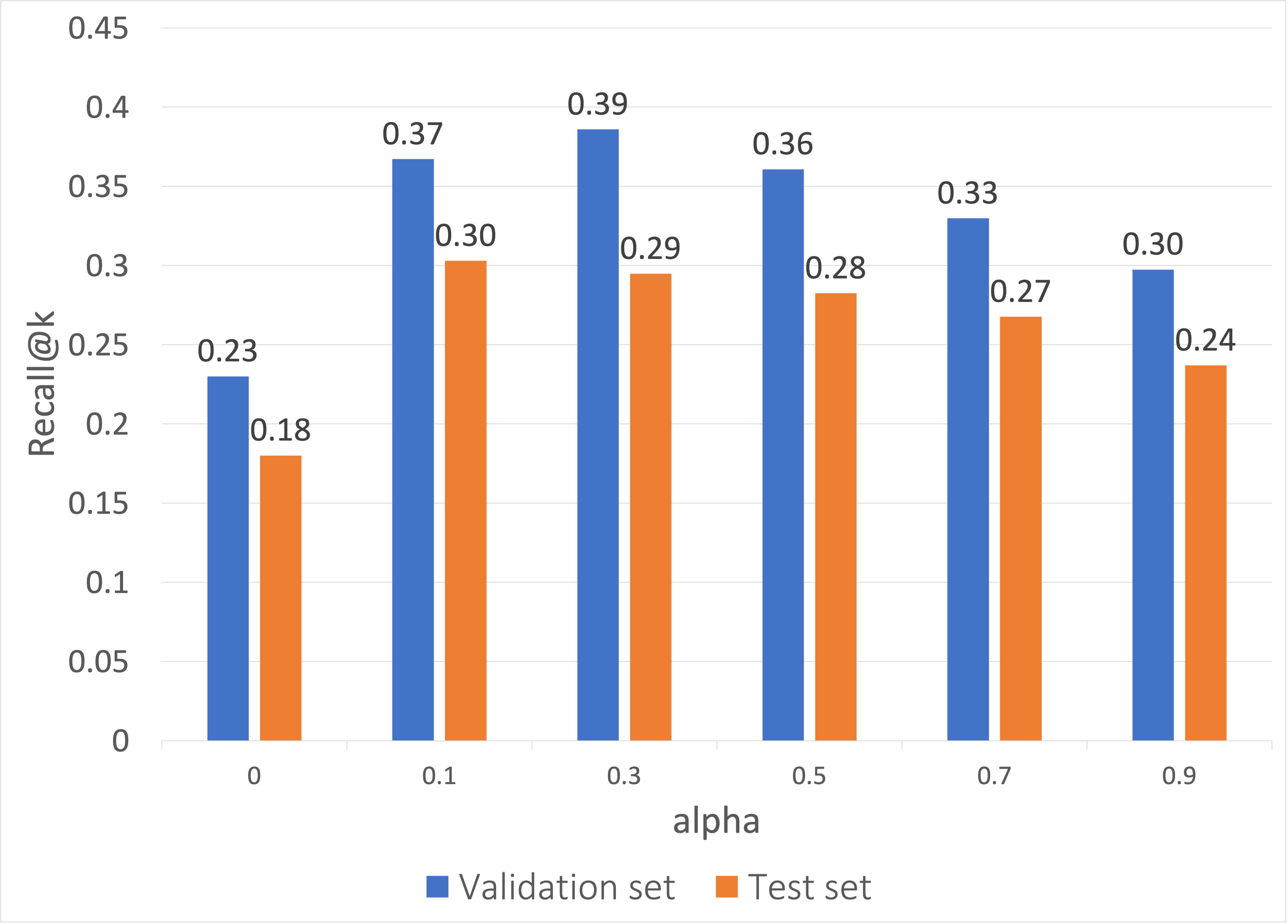
| embedding dimensions | RNN layers | Validation | Test |
|---|---|---|---|
| 64 | 1 | 0.364 | 0.295 |
| 64 | 2 | 0.358 | 0.267 |
| 64 | 3 | 0.383 | 0.310 |
| 32 | 1 | 0.359 | 0.278 |
| 32 | 2 | 0.356 | 0.279 |
| 32 | 3 | 0.386 | 0.302 |
| 16 | 1 | 0.371 | 0.288 |
| 16 | 2 | 0.365 | 0.294 |
| 16 | 3 | 0.370 | 0.290 |
| 8 | 1 | 0.372 | 0.296 |
| 8 | 2 | 0.360 | 0.283 |
| 8 | 3 | 0.331 | 0.266 |
6.5. Discussion
Though our proposed models outperform the existing and extended course recommendation models, there are some limitations. Firstly, they do not penalize popular courses as the ScholarsWalk model does. Consequently, it may introduce popularity bias, meaning that previously popular courses might receive higher recommendation scores compared to other courses with lower popularity. Secondly, similar to other competing approaches, our models cannot recommend new courses as they have not seen these during training. Thirdly, since we do not use course description data, our models do not capture the semantic similarity between courses. Lastly, a user study could be used to practically evaluate the performance of the models in the hands-on scenario. We could survey the current undergraduates, where we recommend them courses, and collect their responses about the quality and suitability of the recommendations.
7. Conclusion
We propose the use of session-based recommendation approaches for recommending suitable and complementary courses for the upcoming semester. Toward that direction, we develop CourseDREAM and CourseBEACON, two session-based approaches that capture the relationship of the co-taken courses in two different ways along with the sequential nature of the course over semesters. We also propose a TF approach, TF-CoC, that captures the relationships between courses co-taken together in a semester. Finally, we propose a post-processing step that could be applied to any course recommendation model to adjust the recommendation scores of the courses based on their correlation. Our experimental results using course enrollment data only show that our proposed models outperform all the competing approaches. We also evaluate if the recommended courses are relevant and well-suited together using different metrics. Overall, our proposed CourseDREAM+CorA exhibits the best performance and behavior. Our models will be helpful in advising students to achieve better performance overall and graduate on time and consequently, reduce the dropout rate in higher education.
References
- Al-Badarenah, A. and Alsakran, J. 2016. An automated recommender system for course selection. International Journal of Advanced Computer Science and Applications 7, 3, 166–175.
- Ariannezhad, M., Jullien, S., Li, M., Fang, M., Schelter, S., and de Rijke, M. 2022. Recanet: A repeat consumption-aware neural network for next basket recommendation in grocery shopping. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM New York, NY, United States, 1240–1250.
- Bendakir, N. and Aïmeur, E. 2006. Using association rules for course recommendation. In Proceedings of the AAAI workshop on educational data mining. Vol. 3. Citeseer, 1–10.
- Bernhardsson, E. 2023. Approximate Nearest Neighbors. Spotify.
https://github.com/spotify/annoy. - Boumi, S. and Vela, A. E. 2021. Quantifying the impact of students’ semester course load on their academic performance. In 2021 ASEE Virtual Annual Conference Content Access.
- Brown, M. G., DeMonbrun, R. M., and Teasley, S. D. 2018. Conceptualizing co-enrollment: Accounting for student experiences across the curriculum. In Proceedings of the 8th international conference on learning analytics and knowledge. ACM New York, NY, United States, 305–309.
- Chen, Q., Guo, Z., Li, J., and Li, G. 2023. Knowledge-enhanced multi-view graph neural networks for session-based recommendation. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM New York, NY, United States, 352–361.
- Chockkalingam, S., Yu, R., and Pardos, Z. A. 2021. Which one’s more work? predicting effective credit hours between courses. In LAK21: 11th International Learning Analytics and Knowledge Conference. ACM New York, NY, United States, 599–605.
- De Medio, C., Limongelli, C., Sciarrone, F., and Temperini, M. 2020. Moodlerec: A recommendation system for creating courses using the moodle e-learning platform. Computers in Human Behavior 104, 106168.
- Diamond, A., Roberts, J., Vorley, T., Birkin, G., Evans, J., Sheen, J., and Nathwani, T. 2014. Uk review of the provision of information about higher education: advisory study and literature review: report to the uk higher education funding bodies by cfe research. Leicester: CRE Research.
- Elbadrawy, A. and Karypis, G. 2016. Domain-aware grade prediction and top-n course recommendation. In Proceedings of the 10th ACM conference on recommender systems. ACM New York, NY, USA, 183–190.
- Entezari, N., Papalexakis, E. E., Wang, H., Rao, S., and Prasad, S. K. 2021. Tensor-based complementary product recommendation. In 2021 IEEE International Conference on Big Data (Big Data). IEEE, 409–415.
- Esteban, A., Zafra, A., and Romero, C. 2018. A hybrid multi-criteria approach using a genetic algorithm for recommending courses to university students. In Proceedings of the 11th International Conference on Educational Data Mining, K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, 273–279.
- Gao, M., Luo, Y., and Hu, X. 2022. Online course recommendation using deep convolutional neural network with negative sequence mining. Wireless Communications and Mobile Computing 2022.
- Gardner, J. and Brooks, C. 2018. Coenrollment networks and their relationship to grades in undergraduate education. In Proceedings of the 8th international conference on learning analytics and knowledge. ACM New York, NY, United States, 295–304.
- Gong, T., Li, J., Yeung, J. Y., and Zhang, X. 2024. The association between course selection and academic performance: exploring psychological interpretations. Studies in Higher Education, 1–14.
- Guo, L., Yin, H., Wang, Q., Chen, T., Zhou, A., and Quoc Viet Hung, N. 2019. Streaming session-based recommendation. In Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining. ACM New York, NY, USA, 1569–1577.
- Hanson, M. 2022. College Dropout Rates. EducationData.org.
https://educationdata.org/college-dropout-rates. - Hu, H., He, X., Gao, J., and Zhang, Z.-L. 2020. Modeling personalized item frequency information for next-basket recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM New York, NY, United States, 1071–1080.
- Hu, Y., Koren, Y., and Volinsky, C. 2008. Collaborative filtering for implicit feedback datasets. In 2008 Eighth IEEE international conference on data mining. IEEE, 263–272.
- Jiang, W. and Pardos, Z. A. 2020. Evaluating sources of course information and models of representation on a variety of institutional prediction tasks. In 13th International Conference on Educational Data Mining, EDM 2020, A. N. Rafferty, J. Whitehill, C. Romero, and V. Cavalli-Sforza, Eds. International Educational Data Mining Society, 115–125.
- Jiang, W., Pardos, Z. A., and Wei, Q. 2019. Goal-based course recommendation. In Proceedings of the 9th international conference on learning analytics & knowledge. ACM New York, NY, USA, 36–45.
- Kadlec, A., Immerwahr, J., and Gupta, J. 2014. Guided pathways to student success perspectives from indiana college students and advisors. New York: Public Agenda.
- Khorasani, E. S., Zhenge, Z., and Champaign, J. 2016. A markov chain collaborative filtering model for course enrollment recommendations. In 2016 IEEE International Conference on Big Data (Big Data). IEEE, 3484–3490.
- Kipf, T. N. and Welling, M. 2017. Semi-supervised classification with graph convolutional networks. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net.
- Le, D.-T., Lauw, H. W., and Fang, Y. 2019. Correlation-sensitive next-basket recommendation. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19. International Joint Conferences on Artificial Intelligence Organization, 2808–2814.
- Ma, B., Lu, M., Taniguchi, Y., and Konomi, S. 2021. Exploration and explanation: An interactive course recommendation system for university environments. In CEUR Workshop Proceedings. Vol. 2903. CEUR-WS.
- Ma, B., Taniguchi, Y., and Konomi, S. 2020. Course recommendation for university environments. In 13th International Conference on Educational Data Mining, EDM 2020, A. N. Rafferty, J. Whitehill, C. Romero, and V. Cavalli-Sforza, Eds. International Educational Data Mining Society, 460–466.
- Malhotra, I., Chandra, P., and Lavanya, R. 2022. Course recommendation using domain-based cluster knowledge and matrix factorization. In 2022 9th International Conference on Computing for Sustainable Global Development (INDIACom). IEEE, 12–18.
- Mondal, B., Patra, O., Mishra, S., and Patra, P. 2020. A course recommendation system based on grades. In 2020 international conference on computer science, engineering and applications (ICCSEA). IEEE, 1–5.
- Morsomme, R. and Alferez, S. V. 2019. Content-based course recommender system for liberal arts education. In Proceedings of the 12th International Conference on Educational Data Mining, C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, 748–753.
- Morsy, S. and Karypis, G. 2019. Will this course increase or decrease your gpa? towards grade-aware course recommendation. Journal of Educational Data Mining 11, 2, 20–46.
- Naren, J., Banu, M. Z., and Lohavani, S. 2020. Recommendation system for students’ course selection. In Smart Systems and IoT: Innovations in Computing, A. K. Somani, R. S. Shekhawat, A. Mundra, S. Srivastava, and V. K. Verma, Eds. Springer, 825–834.
- Obeidat, R., Duwairi, R., and Al-Aiad, A. 2019. A collaborative recommendation system for online courses recommendations. In 2019 International Conference on Deep Learning and Machine Learning in Emerging Applications (Deep-ML). IEEE, 49–54.
- Parameswaran, A., Venetis, P., and Garcia-Molina, H. 2011. Recommendation systems with complex constraints: A course recommendation perspective. ACM Transactions on Information Systems (TOIS) 29, 4, 1–33.
- Pardos, Z. A., Fan, Z., and Jiang, W. 2019. Connectionist recommendation in the wild: on the utility and scrutability of neural networks for personalized course guidance. User modeling and user-adapted interaction 29, 2, 487–525.
- Pardos, Z. A. and Jiang, W. 2020. Designing for serendipity in a university course recommendation system. In Proceedings of the tenth international conference on learning analytics & knowledge. ACM New York, NY, United States, 350–359.
- Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., et al. 2011. Scikit-learn: Machine learning in python. the Journal of machine Learning research 12, 2825–2830.
- Polyzou, A., Nikolakopoulos, A. N., and Karypis, G. 2019. Scholars walk: A markov chain framework for course recommendation. In 12th International Conference on Educational Data Mining, EDM 2019, C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, 396–401.
- Ren, Z., Ning, X., Lan, A. S., and Rangwala, H. 2019. Grade prediction based on cumulative knowledge and co-taken courses. In 12th International Conference on Educational Data Mining, EDM 2019, C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, 158–167.
- Rendle, S., Freudenthaler, C., Gantner, Z., and Schmidt-Thieme, L. 2014. Bpr: Bayesian personalized ranking from implicit feedback. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence (2009). Cornell University, NY, USA.
- Rendle, S., Freudenthaler, C., and Schmidt-Thieme, L. 2010. Factorizing personalized markov chains for next-basket recommendation. In Proceedings of the 19th international conference on World wide web. ACM New York, NY, United States, 811–820.
- Shao, E., Guo, S., and Pardos, Z. A. 2021. Degree planning with plan-bert: Multi-semester recommendation using future courses of interest. In Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 35. AAAI Press, Palo Alto, California USA, 14920–14929.
- Shao, Z., Wang, S., Zhang, Q., Lu, W., Li, Z., and Peng, X. 2023. An empirical study of next-basket recommendations. arXiv preprint arXiv:2312.02550.
- Shen, Y., Ou, B., and Li, R. 2022. Mbn: Towards multi-behavior sequence modeling for next basket recommendation. ACM Transactions on Knowledge Discovery from Data (TKDD) 16, 5, 1–23.
- Sulaiman, M. S., Tamizi, A. A., Shamsudin, M. R., and Azmi, A. 2020. Course recommendation system using fuzzy logic approach. Indonesian Journal of Electrical Engineering and Computer Science 17, 1, 365–371.
- Symeonidis, P. and Malakoudis, D. 2019. Multi-modal matrix factorization with side information for recommending massive open online courses. Expert Systems with Applications 118, 261–271.
- Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, İ., Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and SciPy 1.0 Contributors. 2020. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods 17, 261–272.
- Wagner, K., Merceron, A., Sauer, P., and Pinkwart, N. 2022. Personalized and explainable course recommendations for students at risk of dropping out. In Proceedings of the 15th International Conference on Educational Data Mining, A. Mitrovic and N. Bosch, Eds. International Educational Data Mining Society, 657–661.
- Wan, M., Wang, D., Liu, J., Bennett, P., and McAuley, J. 2018. Representing and recommending shopping baskets with complementarity, compatibility and loyalty. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management. ACM New York, NY, United States, 1133–1142.
- Wang, S., Cao, L., Wang, Y., Sheng, Q. Z., Orgun, M. A., and Lian, D. 2021. A survey on session-based recommender systems. ACM Computing Surveys (CSUR) 54, 7, 1–38.
- Warnes, Z. and Smirnov, E. 2020. Course recommender systems with statistical confidence. In 13th International Conference on Educational Data Mining, EDM 2020, A. N. Rafferty, J. Whitehill, C. Romero, and V. Cavalli-Sforza, Eds. International Educational Data Mining Society, 509–515.
- Wong, C. 2018. Sequence based course recommender for personalized curriculum planning. In International Conference on Artificial Intelligence in Education. Springer, 531–534.
- Yu, F., Liu, Q., Wu, S., Wang, L., and Tan, T. 2016. A dynamic recurrent model for next basket recommendation. In Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval. ACM New York, NY, United States, 729–732.
- Zhang, H., Huang, T., Lv, Z., Liu, S., and Zhou, Z. 2018. Mcrs: A course recommendation system for moocs. Multimedia Tools and Applications 77, 6, 7051–7069.
- Zhang, J., Hao, B., Chen, B., Li, C., Chen, H., and Sun, J. 2019. Hierarchical reinforcement learning for course recommendation in moocs. In Proceedings of the AAAI conference on artificial intelligence. Vol. 33. AAAI Press, Palo Alto, California USA, 435–442.
- Zhu, Y., Lu, H., Qiu, P., Shi, K., Chambua, J., and Niu, Z. 2020. Heterogeneous teaching evaluation network based offline course recommendation with graph learning and tensor factorization. Neurocomputing 415, 84–95.