Abstract
The ability to predict student performance in introductory programming courses is important to help struggling students and enhance their persistence. However, for this prediction to be impactful, it is crucial that it remains transparent and accessible for both instructors and students, ensuring effective utilization of the predicted results. Machine learning models with explainable features provide an effective means for students and instructors to comprehend students’ diverse programming behaviors and problem-solving strategies, elucidating the factors contributing to both successful and suboptimal performance. This study develops an explainable model that predicts student performance based on programming assignment submission information in different stages of the course to enable early explainable predictions. We extract data-driven features from student programming submissions and utilize a stacked ensemble model for predicting final exam grades. The experimental results suggest that our model successfully predicts student performance based on their programming submissions earlier in the semester. Employing SHAP, a game-theory-based framework, we explain the model’s predictions, aiding stakeholders in understanding the influence of diverse programming behaviors on students’ success. Additionally, we analyze crucial features, employing a mix of descriptive statistics and mixture models to identify distinct student profiles based on their problem-solving patterns, enhancing overall explainability. Furthermore, we dive deeper and analyze the profiles using different programming patterns of the students to elucidate the characteristics of different students where SHAP explanations are not comprehensible. Our explainable early prediction model elucidates common problem-solving patterns in students relative to their expertise, facilitating effective intervention and adaptive support.Keywords
1. Introduction
In recent years, there has been a consistent rise in the enrollment of students in introductory programming courses (CS1), reflecting a heightened interest in Computer Science (Sahami and Piech, 2016). However, alongside this surge, there is a parallel increase in the number of students facing challenges and dropping out of these courses (Ihantola et al., 2015, Quille and Bergin, 2019, Watson and Li, 2014). To address this issue, automated prediction systems play a crucial role in forecasting student performance, providing instructors with the means to intervene effectively and prevent academic difficulties (Karimi et al., 2020, Sweeney et al., 2016, Yudelson et al., 2014).
Historically, early methods for predicting student performance in CS1 relied on static approaches utilizing initial student data like age, gender, and grades (Ahadi et al., 2015). However, static prediction proves challenging, as student behaviors are dynamic and can evolve over time (Quille and Bergin, 2019, Sun et al., 2020). In recent years, there has been a shift towards data-driven approaches, particularly leveraging machine learning (ML) techniques (Jamjoom et al., 2021, Lauría et al., 2012, Shahiri et al., 2015, Pereira et al., 2021). However, most of these approaches predominantly analyze intermediate assessment data, such as quiz scores and midterm exam grades, rather than delving into the programming behaviors of students. This limitation hinders these methods from comprehending the root causes of student challenges and makes generalization across different CS1 courses problematic. It is noteworthy that some courses, including the dataset used in this study, may lack interim exams, further emphasizing the need for a more comprehensive analysis.
Moreover, the importance of explainability and transparency in black-box ML models has grown alongside their predictive capabilities. An explainable model holds significance as it aids both instructors and students in comprehending predictions, fostering trust. This transparency allows instructors to delve into students’ problem-solving approaches by discerning patterns in their programming behaviors, facilitating timely interventions to support those encountering difficulties in the learning process (Vultureanu-Albişi and Bădică, 2021, Afzaal et al., 2021). Although some studies have explored explainable performance prediction models in the realm of education (Pereira et al., 2021, Chen et al., 2022), none, to our knowledge, have applied such models to analyze student performance solely based on their programming behaviors, excluding exam or quiz grades from consideration.
In this study, we propose an explainable model for predicting students’ final exam grades solely based on their programming assignment submission data. This task is inherently challenging, especially in courses where the nature of final exams significantly differs from the assignments. To address this, we adopt a data-driven feature extraction approach to identify features that encapsulate student programming behaviors in a CS1 course. Our predictive model is a stacked ensemble regression featuring KNN, SVM, and XGBoost as base models, with linear regression serving as the meta-model. We conduct a comprehensive performance comparison with various baseline techniques, including individual components of our ensemble model (linear regression, KNN, SVM, XGBoost) and other ensemble methods like Bagging and Boosting. The experimental results demonstrate that our proposed model consistently outperforms these baseline techniques. We also show our model’s capability in early prediction based on earlier assignments. The results suggest that our explainable stacked ensemble model can predict student performance early in the course to pave the way to early intervention and help students in a timely manner.
Additionally, we leverage SHAP (SHapley Additive exPlanations) (Lundberg and Lee, 2017), a game-theory-based framework, to elucidate the predictions made by our model. This framework enables us to explore the importance and impacts of individual features in predicting students’ final exam grades both at the individual student level and globally across all students. This explanatory approach allows us to delve into the nuances of student performance prediction, revealing the unique contributions of each feature based on programming behaviors. We perform an in-depth analysis of significant features, employing a combination of descriptive statistics and mixture modeling to discern distinct patterns in student behavior. This analytical insight equips instructors with information on diverse profiles of student learning progressions, aiding in informed decision-making for intervention strategies with struggling students and the provision of adaptive support (Akram et al., 2019).
This study makes significant contributions in the following aspects:
- Development of an explainable stacked ensemble model for predicting student performance in the final exam solely based on students’ programming assignment data and generalizing the model in making early predictions at different stages of the course.
- Providing explanations for the model predictions at both individual and global levels, incorporating various programming information to enhance stakeholders’ trust.
- Conducting a thorough analysis of SHAP results and key features from the explainable model to create student profiles based on behavior and delving deeper into the profiles to understand the characteristics of each profile. This analysis offers insights into students’ problem-solving strategies and their connection to learning outcomes.
2. Related work
This section provides a review of existing techniques and studies within the realm of student performance prediction, specifically focusing on the use of explainable models in the context of programming.
2.1. Student Performance Prediction
Addressing the early prediction of student performance and providing timely interventions is a crucial aspect of intelligent tutoring systems. Researchers have pursued diverse goals in these studies, including predicting early student success, detecting failing students, identifying early dropouts, and forecasting student performance in final exams.
A comprehensive review by Shahiri et al. (2015) highlighted that many studies rely on grading-based features such as cumulative grade point averages (CGPA) and intermediate assessment scores (quizzes, midterms) to predict course performance. Lauría et al. (2012) developed an open-source predictive platform for at-risk student detection, utilizing demographic and enrollment data classified through ML models like SVM and Linear Regression. In a recent study by Jamjoom et al. (2021), Decision Tree and SVM were employed to classify enrolled students into passing and failing categories based on features such as quizzes and midterm exam scores, aiming for early intervention with at-risk students.
Deep learning frameworks have gained prominence in recent studies. Models, such as code2vec (Alon et al., 2019), ASTNN (Zhang et al., 2019), and SANN (Hoq et al., 2023) demonstrated effectiveness in capturing information from student programming codes. In recent studies (Yoder et al., 2022, Marsden et al., 2022), abstract syntax tree-based and control flow graph-based embedding models were employed to predict students’ final exam grades from programming assignment data. Alam et al. (2022) utilized CNN and LSTM networks along with programming code submission metadata to predict student performance on the final exam in an introductory programming course.
Different studies have been conducted to predict student performance or success earlier in a semester or course. Studies such as Costa et al. (2017) and Khan et al. (2019) used features such as weekly assignment scores and midterm exam grades to predict failing students in introductory programming courses. Event-level analysis, specifically predicting success in completing programming exercises, was explored by Mao (2019), who used Recent Temporal Patterns and LSTM. Pereira et al. (2019) predicted early dropout from online programming courses, introducing features from online platforms such as student login times, keystroke latency, and correctness. Another study by Pereira et al. (2021) predicted students’ early performance in an introductory programming course using XGBoost with features including midterm exam grade, procrastination time, correctness, and code-related metrics. In a recent study (Llanos et al., 2023), student performance was predicted earlier in the semester (within the first 3, 5, and 7 weeks) based on the number of programming attempts, delivery time, and an interim exam grade of students. In another recent study (Liu et al., 2023), student final exam grades were predicted after 3 weeks of the semester (five-week online course) using different programming features, such as the number of attempts, correct programs, inactive time, along with demographic data, e.g., gender of students.
Despite the effectiveness of previous studies, several issues persist. Static approaches fail to capture dynamic student behaviors during the learning process. Data-driven approaches may lack generalizability across different programming courses due to variations in course structures and intermediate assessments. In addition, introductory programming courses may lack interim exams, as seen in the dataset used in this study, which consists only of programming assignments. Finally, while deep learning models are gaining popularity, achieving optimal performance with these models on small classroom-sized datasets remains challenging (Mao et al., 2022).
2.2. Explainable Artificial Intelligence (XAI)
Explainable Artificial Intelligence (XAI) is instrumental in unraveling the mysteries of black-box ML models, interpreting outcomes, and shedding light on decision rationales. Its widespread application spans various domains, including medical research, healthcare, clinical data analysis (Muddamsetty et al., 2021, Singh et al., 2021, Kamal et al., 2021), industrial data analysis (Ahmed et al., 2022, Serradilla et al., 2020), and smart city solutions (Thakker et al., 2020, Embarak, 2021). XAI is also gaining prominence in the field of education, ensuring the fairness, transparency, and impartiality of AI systems (Shi et al., 2023). Furthermore, XAI contributes to transparency and accountability in deploying AI in education, fostering trust and responsible technology usage. The ability to personalize learning experiences for individual students through data analysis and tailored instruction is another key benefit, ultimately leading to improved student learning outcomes (Lu et al., 2020, Baranyi et al., 2020, Mu et al., 2020, Vultureanu-Albişi and Bădică, 2021).
Several studies exemplify the application of XAI in educational contexts. For instance, Lu et al. (2020) utilized the layer-wise relevance propagation method to interpret a deep learning-based knowledge tracing model. In another study, Baranyi et al. (2020) employed SHAP to explain outcomes and feature importance in predicting university dropouts using a fully connected deep neural network. Mu et al. (2020) automated individualized intervention by detecting wheel-spinning students repeatedly failing at an educational task, with Shapley values used to explain machine learning model outcomes. Lime (Ribeiro et al., 2016), a technique to explain individual predictions rather than providing a global understanding of the entire model, was applied in Vultureanu-Albişi and Bădică (2021)’s study to interpret ensemble models predicting student performances across various courses and language exams.
Moreover, studies, such as Scheers and De Laet (2021) integrated Lime into Learning Analytic Dashboards, combining explanations and visualizations to predict students’ success. The interactive dashboards illustrated the effects of changes in student features on predictions, with user tests conducted to assess their efficacy. Pei and Xing (2022) used Lime to create an explainable model predicting at-risk students based on student demographic information and clickstream data. In another study by Hasib et al. (2022), different ML techniques were employed to predict high school student performance, with Lime used to explain model outcomes for transparency.
While XAI has gained popularity for interpreting and explaining ML solutions, its effectiveness remains relatively unexplored in the context of Computer Science Education and intelligent tutoring systems. Notably, studies, such as Pereira et al. (2021) and Chen et al. (2022) utilized SHAP and Lime, respectively, to explain success predictions from student data. However, these studies faced limitations, such as a predominant reliance on interim exam grades, such as mid-term exams, and a lack of consideration for real-world scenarios. Moreover, they set a hard threshold of student passing and failing based on the mean course grade, which is not a real-world scenario, as different students may follow different distributions (Sahami and Piech, 2016) in terms of effective and ineffective behaviors (Edwards et al., 2009). For example, learning students might learn from errors and do well at the end, showing seemingly ineffective behavior during the semester, whereas expert students might show a different pattern in consistently performing well. Addressing these gaps, our study focuses on predicting student success in final exams using programming assignment submission information, employing explainable models to enhance transparency and confidence in ML outcomes. Furthermore, we analyze different student profiles to better understand their learning and programming behavior, which can lead to more effective interventions. This profiling approach acknowledges the complex distributions of student behaviors and helps make explanations more lucid for stakeholders, ultimately supporting more tailored and effective educational interventions.
3. Dataset
In this study, we use a publicly available dataset 1 collected from the CodeWorkout platform 2. CodeWorkout (Edwards and Murali, 2017) is an online platform that helps students practice programming in Java and allows instructors to design learning activities in their programming courses. CodeWorkout logs student programming code submission information associated with different assignments. These assignments test the student’s knowledge of basic programming concepts, such as data types, arrays, strings, loops, conditional statements, and methods.
The dataset encompasses two semesters, Spring 2019 and Fall 2019, featuring a total of 772 students. In each semester, 50 programming problems are distributed across 5 assignments (Each assignment with different concepts, e.g., loops, conditionals, arrays, strings), with 10 problems per assignment. Students can submit each problem multiple times without any fixed deadline. Scores for each problem submission fall within the (0, 1) range, determined by the number of passing test cases. A perfect submission achieving correctness across all test cases receives a score of 1. The dataset comprises code submissions for each problem and other information, some detailed in Table 1.
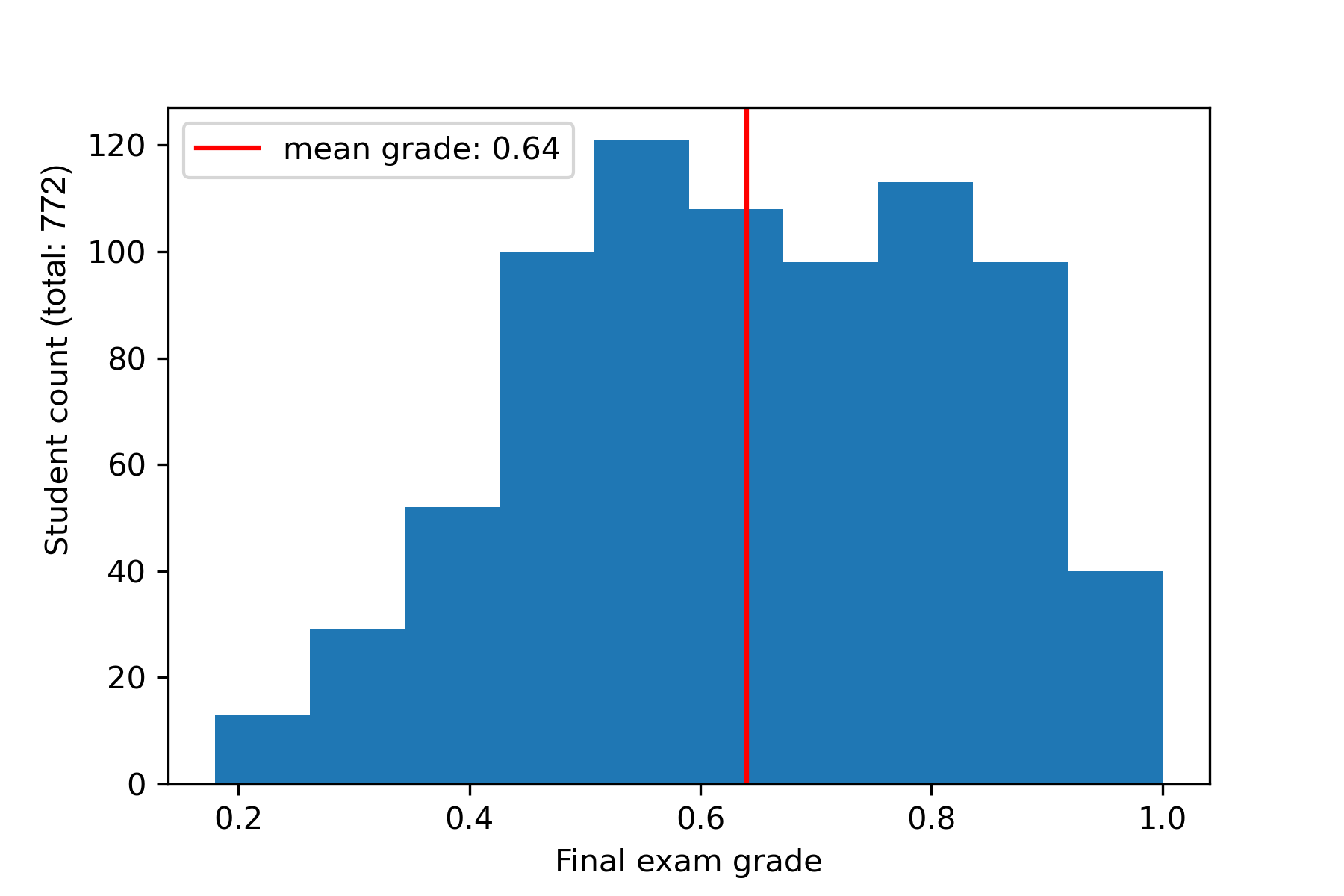
The CodeWorkout dataset also includes the final exam grades of the students, normalized within the range of 0 to 1. The distribution of final exam grades is visualized in Figure 1, indicating a mean final exam grade of 0.64, accompanied by a standard deviation of 0.18, denoted by a red vertical line. This study focuses on predicting students’ final exam grades based on their performance in programming assignments throughout the course.
4. Methodology
In our endeavor to forecast students’ final exam grades utilizing their programming submission data and elucidate the rationale behind the predictive model’s decisions, we adhere to three key steps: i) Conducting feature engineering and extracting data-driven features from the programming submission data, ii) Constructing and deploying regression models for final exam grade prediction, and iii) Employing SHAP to provide explanations for the model’s decisions. The comprehensive architecture of the model is depicted in Figure 2.
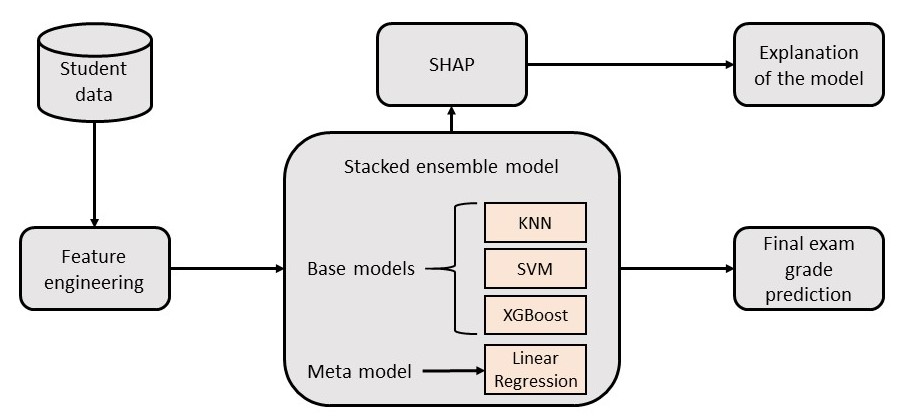
4.1. Feature Engineering
We opt for various features linked to students’ programming submissions, encompassing total programming time spent (TimeSpent), the count of unique problems attempted (Valid), the count of correct submissions (CorrectSub), the count of incorrect submissions (IncorrectSub), the count of uncompilable submissions (CompileError), total scores in all submissions (Scores), and total changes in codes (EditDistance). These are the features that could be extracted from the current dataset and that have been used in previous studies (Pereira et al., 2021, Carter et al., 2019, Castro-Wunsch et al., 2017, Estey and Coady, 2016, Edwards et al., 2009). A detailed description of these features is provided below, and their values are normalized to fit within the range of 0-1. A statistical overview of these features is presented in Table 2. Here, each feature is calculated at the student level, and an average for the students in the course is shown.
| Feature | Mean (std) | Normalized mean (std) |
|---|---|---|
| TimeSpent | 531225.7 (830164.3) | 0.07 (0.09) |
| Valid | 44.88 (9.6) | 0.93 (0.11) |
| CorrectSub | 45.96 (14.03) | 0.41 (0.08) |
| IncorrectSub | 85.30 (83.95) | 0.15 (0.12) |
| CompileError | 87.43 (65.0) | 0.16 (0.11) |
| Scores | 38.0 (9.4) | 0.80 (0.13) |
| EditDistance | 845.3 (476.2) | 0.32 (0.16) |
- TimeSpent: It is calculated using the ServerTime of each problem submission. The difference between the first submission for a problem and the final submission is calculated for each problem. The total time spent by a student is measured by adding these time differences for all attempted problems of that student. This represents how much time a student has spent solving the problems. It is important to note that this measure only accounts for the time between the first and the final submission of each problem. The time spent by a student before making the first submission is not captured in this dataset, as there is no available data on when a student began working on a problem. Therefore, TimeSpent represents the amount of time a student has actively engaged with the assignments, as reflected by their submission activity.
- Valid: It counts the number of unique programming problems that a student has attempted from the total of 50 problems available. A problem is considered “attempted” if the student has submitted at least one solution, regardless of whether the submission was correct, incorrect, or failed to compile.
- CorrectSub: It is the number of correct compilable submissions out of all the problems. These submissions pass all test cases and obtain a score of 1 out of 1.
- IncorrectSub: It is the count of incorrect submissions submitted by a student. These are compilable codes with scores less than 1 and fail some of the test cases.
- CompileError: It is the total number of uncompilable codes a student submits. These codes contain one or more syntax errors that the system compiler outputs, so test cases cannot be tested on them. These submissions do not have any scores.
- Scores: Each problem can have multiple incorrect and correct submissions and, thus, multiple scores. These scores are averaged by the total number of submissions for a problem to have a single score for each problem. After that, the average scores of each problem are summed up to get the total average score for that student.
- EditDistance: It is the measure of how much a student has changed the code in subsequent submissions for each problem. It is calculated between pairs of consecutive submissions for each problem using the Levenshtein algorithm. After that, edit distances for all problems are summed to get an idea of a student’s code change throughout the semester.
4.2. Predictor Model for Prediction
In this study, we construct a stacked ensemble regression model (Wolpert, 1992) designed to amalgamate the predictive capacities of diverse ML models. Employing a meta-learning strategy, this model leverages the strengths of various models to formulate a comprehensive prediction. The ensemble model aims to improve predictive efficacy beyond what each individual predictor model can achieve (Ting and Witten, 1997). Given the presence of multiple predictor models, stacking involves the incorporation of another model that learns when to utilize or place trust in the ensemble models.
Unlike other ensemble models like bagging or boosting, stacked ensemble models exhibit a unique approach. While bagging combines decisions from numerous decision trees, stacked models, in contrast, typically feature a diverse set of models in their stacking composition, not limited to decision trees. In boosting, each ensemble model endeavors to rectify predictions made by the preceding models. In contrast, stacking incorporates another ML model that learns the optimal way to amalgamate predictions from the contributing models. In this study, bagging and boosting serve as baseline models.
Therefore, the architecture of a stacked model can be divided into two model categories:
- Base models (Level 0): Models that are stacked and fit on the dataset and whose predictions are combined later.
- Meta model (Level 1): Model that learns how to combine and trust the predictions of the base models.
In this research, the base models encompass KNN, SVM, and XGBoost, with the metamodel being linear regression, which is responsible for consolidating predictions from the base models. The selection of diverse ML models as base models is intentional, introducing varied assumptions about the prediction task. In contrast, the meta-model, typically simpler, aims to offer a coherent interpretation of predictions generated by the base models (Hoq et al., 2023).
The meta-model undergoes training using predictions generated by the base models on hold-out data. This hold-out data, a subset of the dataset excluded from the base models during training, is subsequently used to obtain predictions from the base models. These predictions and the corresponding expected outputs form the input and output pairs for training the meta-model. To ensure proper training of the stacked ensemble model, we adopt repeated K-fold cross-validation, employing 10 folds and 10 repeats.
4.3. Baseline Models
No-skill: As our no-skill baseline model, we opt for the mean final exam grade. This simplistic model predicts the average of all students’ final exam grades without utilizing any specific knowledge for the prediction.
ML models: We also use different models to compare the performance of our stacked ensemble model. We choose individual baseline models to see the difference in performance between our stacked ensemble model and the baseline models individually. We also use bagging and boosting to see the difference with other ensemble models. We tune the parameters of the models individually using a repeated 10-fold cross-validation approach.
- Linear regression
Linear regression is a simple model that assumes a linear relationship between inputs and outputs. - K-Nearest Neighbors
KNN stores all the available data points from the training data and predicts from \(k\) neighbors’ target values based on a distance function. We select \(k\) = 20 and use Manhattan distance to find the neighborhood for the best result using repeated 10-fold cross-validation. - Support Vector Machine
SVM can acknowledge the presence of non-linearity in data when used in regression tasks. We set the \(kernel\) to \(rbf\) and the regularization parameter \(C\) to 1 for the best results. - Extreme Gradient Boosting
XGBoost is an efficient gradient-boosting-based ensemble algorithm. It outperforms other ensemble algorithms with its high efficiency and faster nature due to the parallelization of trees. We set the parameters \(max\_depth\) = 6, \(n\_estimator\) = 20, and \(gamma\) = 1 for the best result. - Bagging
Bagging is an ensemble model that combines the output of many decision trees. We set \(n\_estimator\) = 10, and \(max\_features\) = 1 for the best result. - Boosting
We use a Gradient Boosting regressor to represent boosting. In Boosting, each model tries to minimize the error of the prior predictor models. We set \(loss\) to \(squared\_error\), \(learning\_rate\) = 0.1, and \(n\_estimators\) = 100 for the best result.
4.4. Explainable Artificial Intelligence (XAI) Using SHAP
Explainable Artificial Intelligence (XAI) is crucial in education, particularly in the context of ML models used to predict student performance. Unlike traditional black-box models, XAI provides transparency by offering clear explanations for the decisions made by these models. In the realm of education, understanding the reasoning behind predictions is vital for both instructors and students. Interpretable models not only shed light on the effectiveness of students’ problem-solving strategies but also enable instructors to deliver targeted and constructive feedback. This transparency fosters trust among students and educators, contributing to a more supportive and effective learning environment.
In this study, SHapley Additive exPlanation (SHAP; Lundberg and Lee 2017) is employed as a critical tool for enhancing the transparency and explainability of our model. SHAP, a model-agnostic algorithm based on Game Theory (Shapley, 1952), efficiently dissects prediction variability by attributing it to individual features within a predictive model. This enables the measurement of both global and local contributions and the importance of each feature, ensuring a comprehensive understanding of the model’s decision-making process (Joseph, 2019).
SHAP calculates Shapley values for each feature for each instance. These values determine the presence of each covariate in the model predictions as a linear combination of each predictor variable. To calculate the positive or negative effect of each feature on the predictions, the algorithm examines the change in each prediction when a feature \(i \in F\) is withheld, where \(F\) is the set of all features (Lundberg and Lee, 2017). Thus, the feature importance of a feature \(i\) for a model \(f\) is calculated by the evaluation of the marginal contribution \(\Phi _i \in \mathbb {R}\) for all the subsets \(S \subseteq F\). According to Lundberg et al. (2018), to satisfy local accuracy, consistency, and missingness properties, \(\Phi _i\) (Shapley value) is defined as: \[\Phi _i = \sum _{S\subseteq F\setminus \{i\}} \frac {\vert S\vert ! (\vert F \vert - \vert S \vert -1)!}{\vert F \vert !} [f_{S\cup \{i\}}(x_{S\cup \{i\}}) - f_S(x_S)]\] Where, \(\Phi _i\) is the marginal contribution of feature \(i\) on the model’s output \(f_{S\cup \{i\}}(x_{S\cup \{i\}})\).
By the additive property, SHAP approximates each prediction \(f(x)\) of the model with the help of \(f'(y')\) which is a linear combination of all binary variables \(y' \in \{0, 1\}^N\) (\(N\) is the maximum size for the simplified feature vectors) and the marginal contributions of each feature \(\Phi _i\) in such a way that the sum of all the feature contributions should match the output of \(f\) for a simplified input \(y'\):
\[f(x) = f'(y') = \Phi _0 + \sum _{i=1}^{N} \Phi _i \cdot y'_i \]
Where, \(\Phi _0\) is the expected prediction without any prior information, in our case, the average final exam grades of students. In a nutshell, Shapley values approximate a model’s predictions locally for a given variable \(x\) (local accuracy). It tries to ensure that the contribution of a variable is zero when the variable is zero (missingness). If the contribution of a variable is higher in the model’s prediction, then the Shapley value for that variable should also be higher (consistency). By leveraging Shapley values, we gain insight into the contributions of different features within the model, allowing us to elucidate the rationale behind model predictions.
The application of SHAP in our analysis not only fosters a deeper understanding of the model’s decision-making process but also provides a foundation for profiling students based on their problem-solving strategies, further bolstering the transparency and utility of our predictive model.
5. Results
In this section, we evaluate the performance of our proposed stacked ensemble model in students’ final exam grade prediction. Later, we interpret the black-box model by analyzing the importance and impact direction of each of the features using SHAP. We further analyze the influence of the most important features on the final exam grades to categorize students into different profiles based on their performances. Finally, we look into the profiles and investigate the consistency of the characteristics during the early predictions.
5.1. Evaluation
In the first phase of our prediction, we use all 5 assignments in the course to predict students’ final exam grades. We compare our results with the base models, the meta-model, and other ensemble models individually. Therefore, we experiment with Linear regression, KNN, SVM, XGBoost, Bagging, and Boosting for the same task. We also use a no-skill model, which predicts the mean final exam grade. This acts as a naive baseline model without prior knowledge of the features. All models are evaluated using a 10-fold cross-validation approach with ten repeats to get a stable result.
To compare the performances of these models, we measure the root-mean-square error (RMSE) of the predicted final exam grades with respect to the actual final exam grades. Since RMSE follows the same range (0-1) as our final exam grades, it can provide insights into how far the predicted values are from the actual ones. Moreover, it penalizes large errors. This makes it a suitable metric to evaluate the model performances since models with a consistent and stable accuracy level are more useful than models with more errors, and RMSE gives relatively high weight to large errors (Yoder et al., 2022). Along with RMSE, we also use the coefficient of determination, \(\mathrm {R^2}\), as an evaluation metric. \(\mathrm {R^2}\) shows how much of the variation in the dependent variable is accounted for by the independent variables in a regression model.
| Model | RMSE (\(\downarrow \)) | \(\mathrm {R^2}\) (\(\uparrow \)) |
|---|---|---|
| no-skill | 0.247 (0.020) | -0.01 (0.018) |
| KNN | 0.173 (0.004) | 0.37 (0.10) |
| Linear | 0.185 (0.004) | 0.38 (0.08) |
| XGBoost | 0.170 (0.005) | 0.39 (0.09) |
| Bagging | 0.166 (0.004) | 0.44 (0.09) |
| Boosting | 0.161 (0.003) | 0.47 (0.08) |
| SVM | 0.159 (0.003) | 0.51 (0.10) |
| Stacked ensemble | 0.151 (0.003) | 0.55 (0.07) |
Table 3 shows the performance of the regression models based on RMSE values and \(\mathrm {R^2}\) scores. These values are calculated by taking the average of the repeated cross-validation results. The standard deviation of each model is also calculated and shown in parentheses with the average RMSE and \(\mathrm {R^2}\). We can see that all the regression models outperform the naive baseline model with no skill. Our stacked ensemble regression model outperforms all other models with an RMSE of 0.151 and an \(\mathrm {R^2}\) score of 0.55. We further investigate the performance of our model statistically to see if the model’s performance is significantly different from other models. We use the Wilcoxon-signed rank test with a significance level of 0.05. The null hypothesis is that the performance of our model is the same as any other baseline model. The null hypothesis is rejected for all the baseline models (p-value\(<\)0.05). These results demonstrate that our model shows statistically significant improvement over the performances of other models.
5.2. Early Prediction
One crucial aspect of enhancing the educational experience is the ability to predict student performance early in a course, allowing for timely interventions and the provision of personalized instructional support. This proactive approach not only aids instructors in understanding students’ challenges but also facilitates impactful support, ultimately contributing to a healthy learning trajectory for students (Jamjoom et al., 2021, Mao, 2019).
The dataset used in this study lacked predefined deadlines for student submissions. Students were free to submit assignments in any order and at any time, posing a challenge for early prediction based on temporal factors. However, upon a close inspection of the dataset, we realized that a striking 95% of the students adhered to a consistent and ordered sequence in their assignment submissions, even in this system where students can submit assignments at any time of the semester. This unique pattern allowed us to devise a strategy for early prediction not based on the time elapsed in the course (i.e., within the first 2 weeks, first 2 months) but rather on the completed assignments submitted during the course.
We employed our stacked ensemble model to predict students’ performance at various stages of their problem-solving. Specifically, our analysis considered predictions derived from students’ submissions to the first assignment, the first two assignments, the first three assignments, the first four assignments, and all five assignments (without any early prediction). The results are shown in Table 4.
| Assignment subsets | RMSE | \(\mathrm {R^2}\) |
|---|---|---|
| first 1 assignment | 0.201 (0.008) | 0.35 (0.08) |
| first 2 assignments | 0.19 (0.007) | 0.43 (0.04) |
| first 3 assignments | 0.178 (0.004) | 0.50 (0.07) |
| first 4 assignments | 0.17 (0.008) | 0.51 (0.03) |
| all (5) assignments | 0.151 (0.003) | 0.55 (0.07) |
The results from our early prediction model, detailed in Table 4, reveal a notable trend in predictive performance based on the growing subset of assignments considered for the prediction. As the number of assignments included increases, both RMSE and \(\mathrm {R^2}\) show consistent improvement, with the most comprehensive model, incorporating all five assignments, achieving the lowest RMSE of 0.151 and the highest \(\mathrm {R^2}\) of 0.55, as the final exam grade range is from 0 to 1. However, using subsets of the assignments also shows promising results in predicting student performance at an earlier stage of the course. This indicates the model’s efficacy in predicting student performances even in the absence of a structured timeline for completing the assignments, where students can submit the assignments at any time of the semester. The analysis underscores the practicality of our approach in providing early insights, with considerations for time-demanding interventions in real-world educational settings. The diminishing RMSE and escalating \(\mathrm {R^2}\) demonstrate the model’s ability to adapt to unconventional dataset structures, where students can submit assignments at any time of the semester. These results suggest that our model can contribute meaningfully to personalized feedback and timely interventions, which is the future direction of this study (Mao, 2019).
5.3. Unfolding the Blackbox Model
To better understand the underlying mechanism behind the stacked ensemble model’s predictions, we calculate the Shapley values, values that determine the importance and impact direction of each feature, using the SHAP algorithm. Using SHAP, we can get the interpretation at an individual level for a student as well as a global level for all students. It enables us to understand the model predictions in a transparent way.
5.3.1. Individual Level Explanation
At first, we look at an individual student’s final exam grade prediction made by the model. Figure 3 shows a force plot for an individual student whose actual final exam grade is 0.61. \(f(x)\) is the model’s prediction which is 0.59. The base value is 0.64, which is the mean final exam grade. This is the prediction of the no-skill model if there is no prior knowledge about the features. The plot also shows the most important feature names and their corresponding values for this prediction. The red-colored features pushed the predicted final grade higher, and the blue features pushed the grade lower. The longer the arrow is, the larger the impact of that feature on the decision. Low EditDistance and CompilerError, and high Valid helped the predicted grade to be higher, whereas high Scores and TimeSpent pushed the grade to be lower. This shows a counterintuitive pattern of the Scores feature impact on the student’s final exam grade. We investigate it further in the later part of this study.

5.3.2. Global Level Explanation
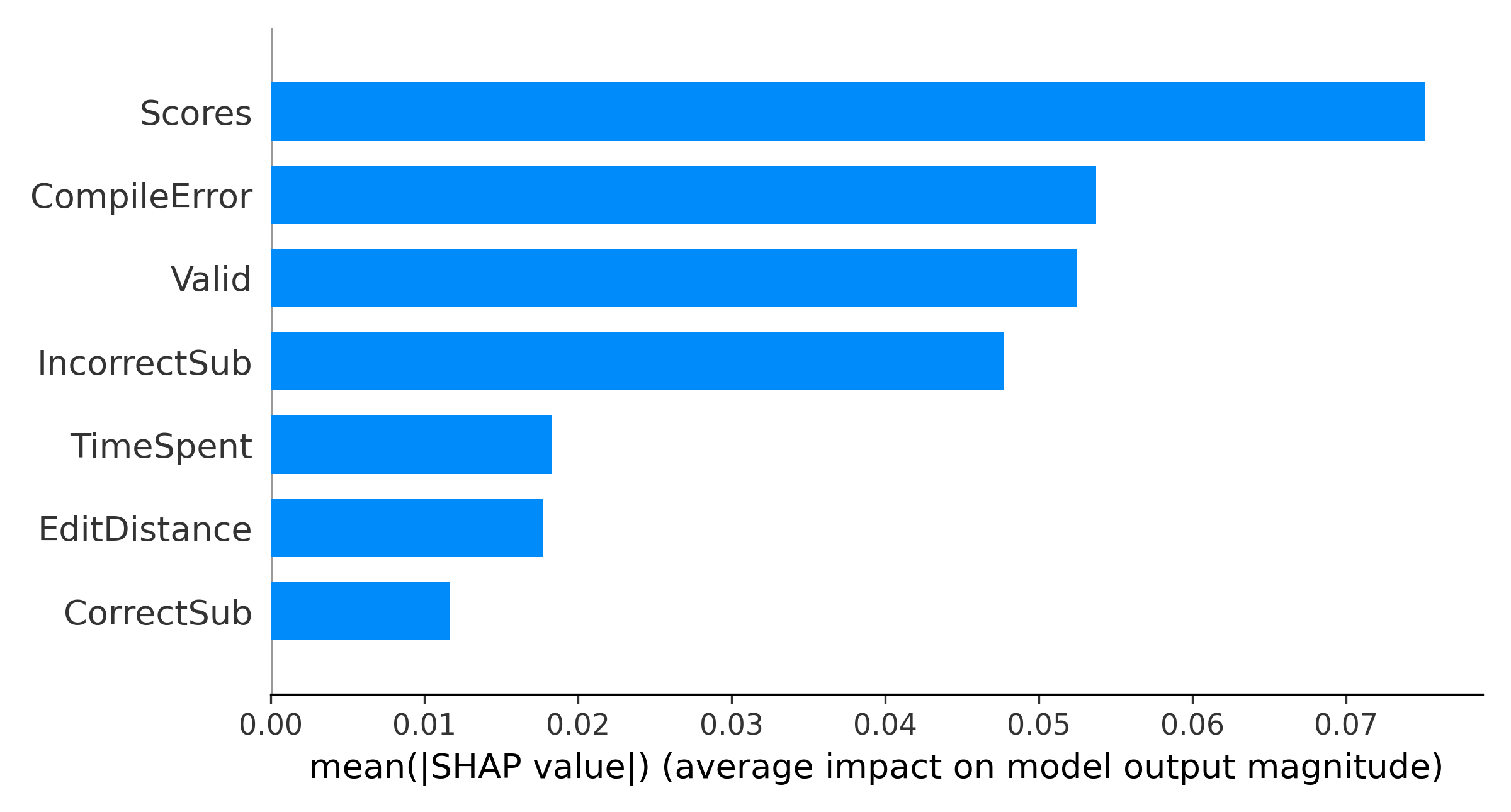
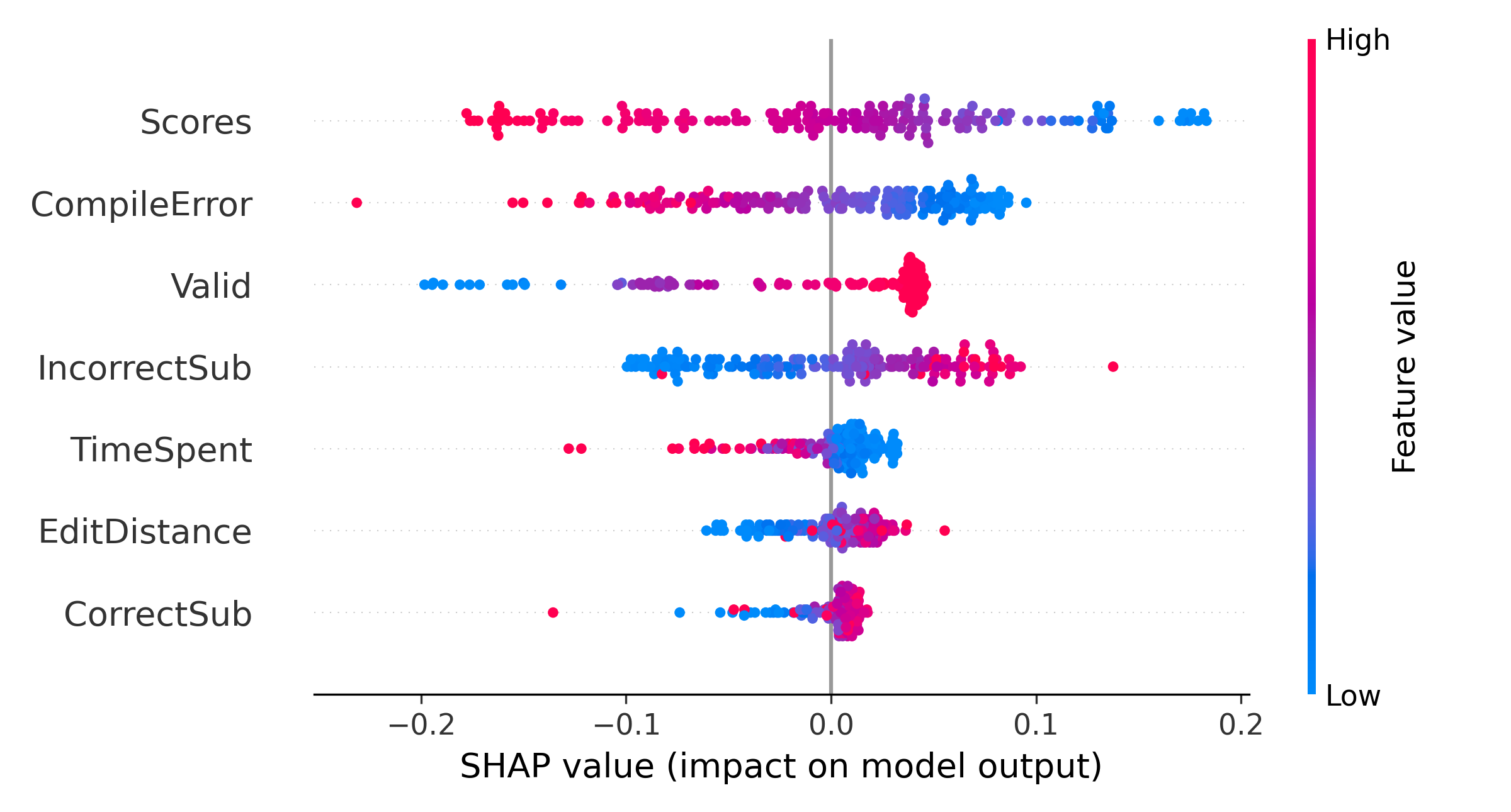
We plot the relative importance of features in Figure 4 using SHAP to understand the force plot more clearly and to comprehend the relative importance of features at a global level for all the students. The X-axis represents the relative importance of the features on the model’s predictions. We can see that Scores is the most important feature, whereas CorrectSub is the least important. We also plot the summary of all the features for all students to understand the relationship between feature values and predicted values in Figure 5. In the summary plot, the features are ranked by importance. Each point represents the Shapley value for each feature regarding prediction for a single data point. Overlapping points are jittered around the Y-axis to get an idea of the distribution of the Shapley values. Red represents a high value for that feature, and blue represents a low value. The summary plot shows that students with high CompileError, low Valid, high TimeSpent, low EditDistance, and low CorrectSub have negative Shapley values, which correspond to a higher probability of performing poorly in the final exam. Therefore, students with a relatively high number of compiler errors, low number of attempted assignments, high amount of time spent on submitting the assignments, low changes or edits in subsequent submissions, and low number of correct assignments have negative Shapley values, which correspond to a lower final exam grade.
On the other hand, the feature impact of Scores and IncorrectSub on students’ final grades are demonstrated as counterintuitive results based on the summary plot. We can see that some students with lower scores tend to have higher grades in the final exam, while some students with higher scores do not do well in the exam. Similarly, some students with a higher number of incorrect submissions do well in the final exam, while some students with a lower number of incorrect submissions achieve poor grades in the exam. We hypothesize that this observation can be explained by looking more closely at students’ programming behavior, including their average edit distance in each submission. Other prior works have used the edit distance to group students based on their problem-solving behavior and identify effective problem-solving patterns based on each group’s performance (Jadud, 2006, Edwards et al., 2009, Akram et al., 2018, Akram et al., 2019). Thus, we hypothesize that the interaction between scores, incorrect submissions, and edit distance can be deterministic of students’ learning. To investigate our hypothesis, we discretized the values for scores and the number of incorrect submissions features into low and high values using Gaussian Mixture Modeling (GMM) (Sahami and Piech, 2016). GMM can be used for clustering where, probabilistically, each data point is assumed to be generated from a mixture of a finite number of Gaussian distributions where the parameters are unknown. It uses the Expectation-Maximization (EM) algorithm to determine these parameters. Each Gaussian distribution is specified by its mean and covariance.
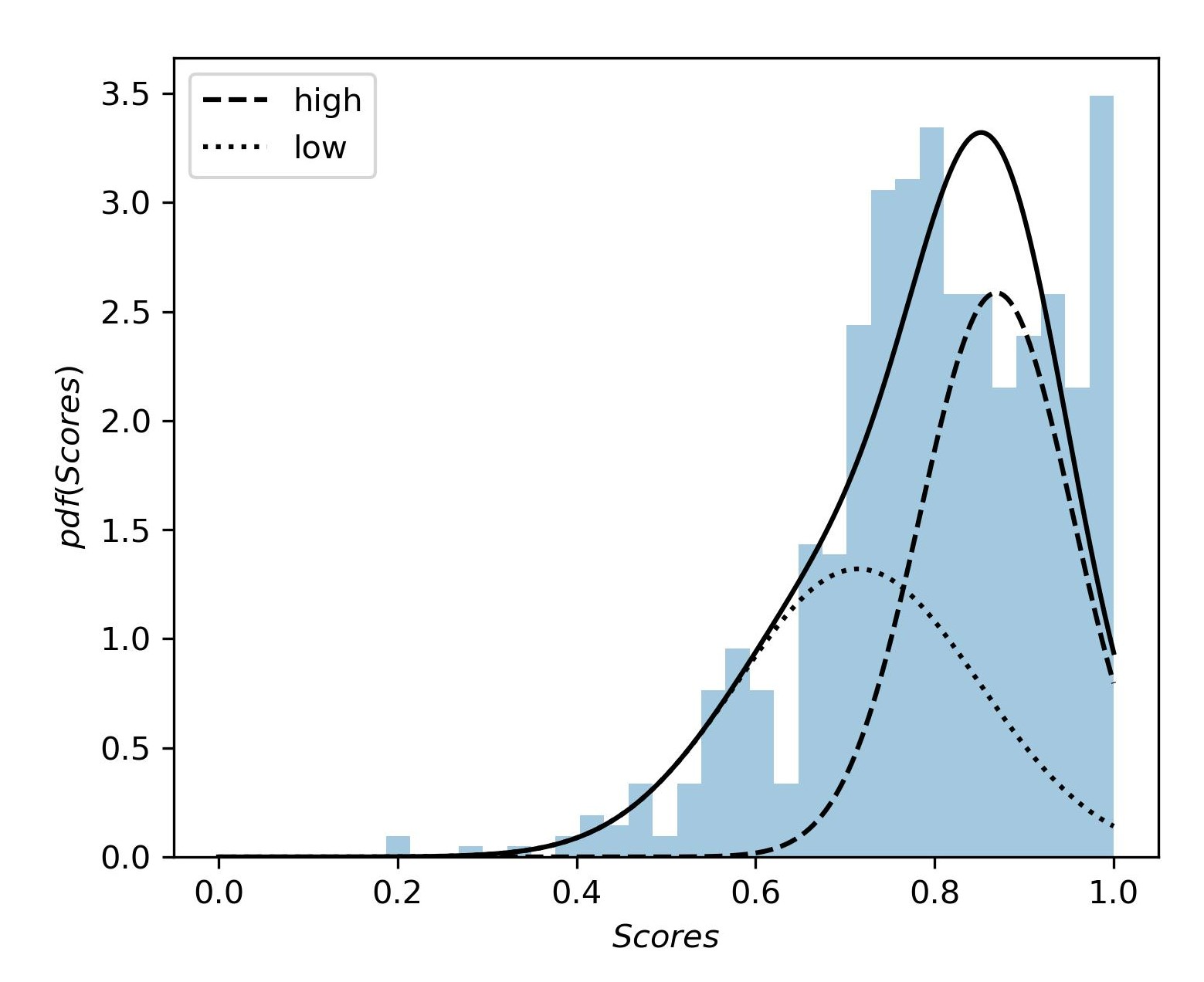
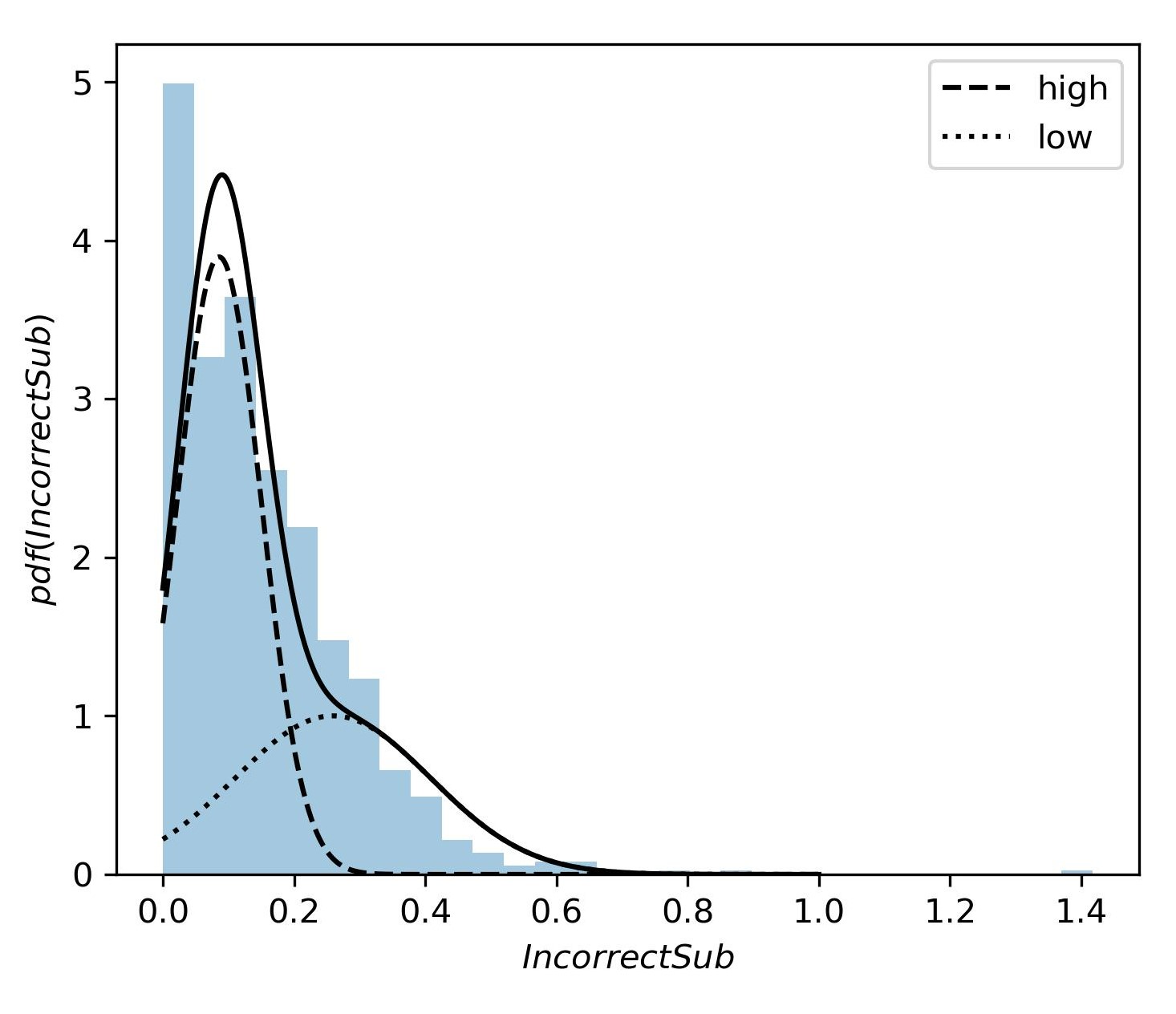
We use Gaussian Mixture Modeling to divide each feature distribution into two components: “component low” and “component high”. Students belonging to “component low” have a relatively lower value, and “component high” has relatively higher values for that individual feature. Figure 6 shows the components of the feature Scores where “component low” has a mean score value of 0.71 and “component high” has a mean Scores value of 0.87. The X-axis shows the probability density function (pdf) of Scores, which is proportional to the likelihood of observing a particular average assignment score among the students. Similarly, figure 7 shows the components of the feature IncorrectSub, where “component low” has a mean IncorrectSub value of 0.08, and “component high” has a mean IncorrectSub value of 0.26. From the components of each feature obtained from Gaussian Mixture Modeling, we get the students of “component low” for each feature whose probability of being assigned to “component low” is higher than that of being assigned to “component high”. Similarly, we get the students who belong to “component high” for each feature. After investigating the interactions between these two features, students’ final exam grades, and also taking the impact of edit distance into account, three main student profiles were identified and named with the help of experienced CS educators based on possible values for the number of incorrect submissions and their average programming assignment scores (Boroujeni and Dillenbourg, 2018, Lorenzen et al., 2018, Loginova and Benoit, 2021). These profiles are demonstrated in Table 5, along with each profile’s average final grades.
| Scores | IncorrectSub | Student Profile | Final exam mean (std) | Student count |
|---|---|---|---|---|
| low | high | Learning | 0.72 (0.14) | 168 |
| low | low | Struggling | 0.60 (0.18) | 120 |
| high | low | Expert | 0.80 (0.08) | 261 |
| Anomaly | 0.48 (0.10) | 152 | ||
| high | high | Outlier | 0.68 (0.19) | 71 |
5.4. Student Profiling
As discussed previously, we further analyze the explanations of the model’s predictions to profile students based on their learning outcomes and strategies.
5.4.1. Expert or Anomaly Students
Students who have a high score and a low number of incorrect submissions, on average, have a mean final exam grade of 0.58. This grade is 0.06 lower than the overall mean grade (0.64). We hypothesize that students who submit a low number of incorrect submissions with a high score on average are either experts or anomalous students who show a different pattern than expected, and thus, we expect to see a noticeable difference between the average final grade for these two sets of students.
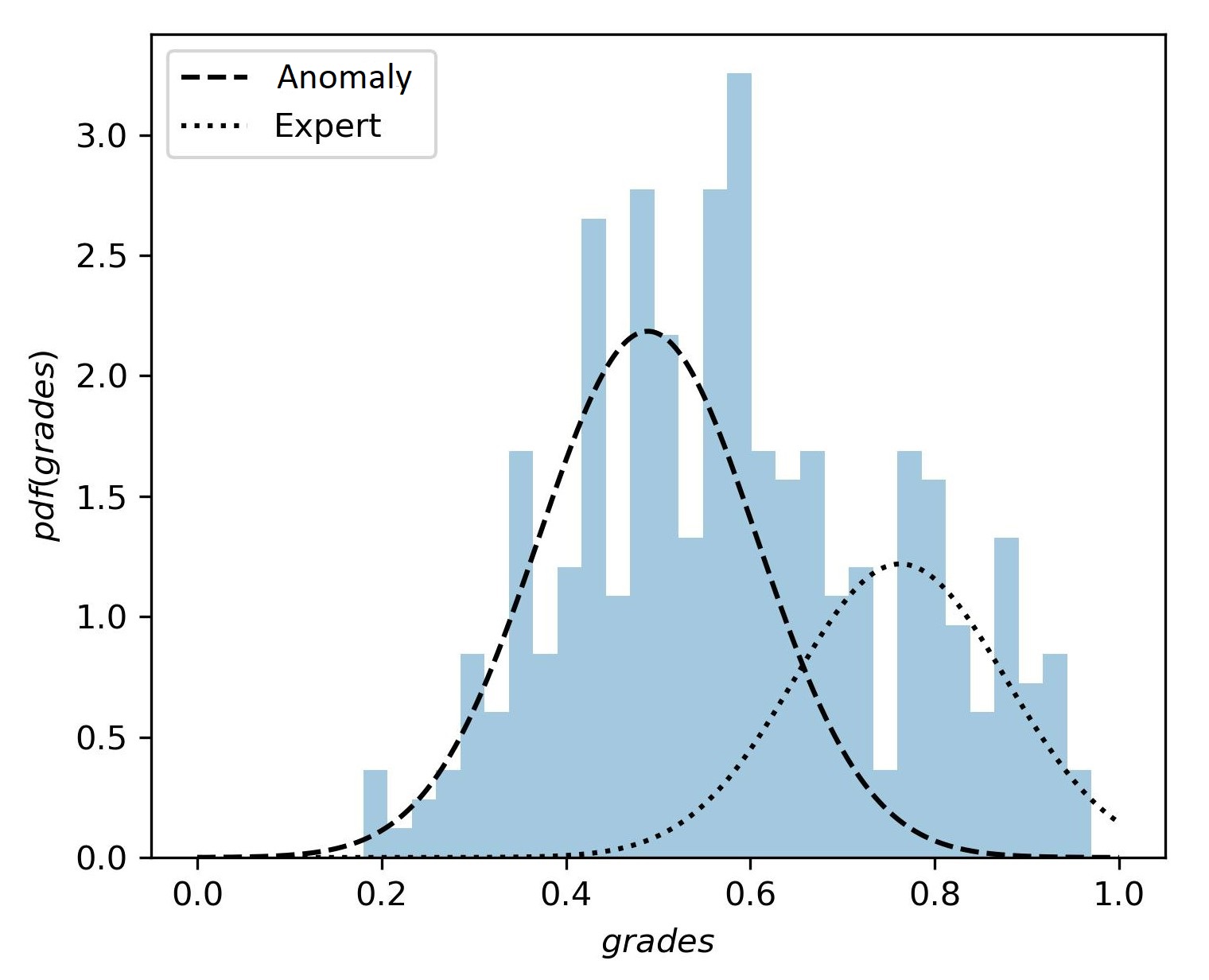
To test this hypothesis, we divide these students into expert and anomaly profiles based on their final exam grades and check the mean grades of these two profiles to determine whether there is a significant difference between them. The anomaly group has a mean final exam grade of 0.48, and the expert group has a mean final exam grade of 0.80. We perform an independent sampled t-test to compare the mean grades of the two profiles. The grades of these two profiles are significantly different with a p-value of less than 0.05. We further verify our hypothesis using Gaussian Mixture Modeling and dividing the final exam grade distribution of this profile into two components (Sahami and Piech, 2016) as illustrated in Figure 8. The component with a high mean grade (0.79) represents the expert group, and the component with a low mean grade (0.49) represents the anomaly group. This is a clear indication that there is a significant difference in the competency of both groups. The students in the anomaly group show unusual patterns compared to the expert students. These students might be doing well on the programming assignments but doing badly on the final exam. The lower final exam performance of students in the anomaly group, compared to expert students, can be attributed to multiple factors, such as cheating (Sheard et al., 2003), surface learning (de Raadt et al., 2005), expedient help-seeking (Ryan and Shim, 2012), or exam anxiety (Trifoni and Shahini, 2011). Although we are not analyzing the reasons behind this anomalous behavior, these students require expert intervention, which can be facilitated through this study.
5.4.2. Learning Students
The second profile of students we investigate are the students with a high number of incorrect submissions and a low score on average. This group has a mean final exam grade of 0.72, which is 0.08 higher than the total average mean grade. About 84% of these students have a high edit distance on average. This suggests that many students without solid background knowledge learn through trial and error by attempting different solutions multiple times.
5.4.3. Struggling Students
Students who have a low number of incorrect submissions and lower scores on average are identified as struggling students. This group has a mean final exam grade of 0.6, which is 0.04 points lower than the mean grade of all students. About 89% of these students have a low edit distance on average. The mean EditDistance for this group is 0.2, which is 0.12 points lower than the average edit distance for all students. They also have a mean of 0.3 points for the number of correct submissions, which is 0.11 points lower than the average number of correct submissions.
5.4.4. Outlier
The last group of students is formed by students who have a high number of incorrect submissions and a high average score. This group of students constitutes as low as 10% of the total data set and, therefore, is not investigated further and is not included in any particular profiles.
Overall Summary: These results suggest that, while expert students can get the desired outcome through a few high-quality attempts, students with moderate levels of knowledge and expertise aim for the desired results through multiple incorrect submissions, attempting new solutions for each submission. On the lower end of the spectrum, struggling students would not put significant effort into engaging with the activities compared to expert and learning students, as demonstrated by the low number of submissions with a low score on average. These analytical results explain why features Scores and IncorrectSub have an atypical effect on the model’s predictions.
5.5. Delving deeper into the profiles
In the previous section, we divided the complex student distribution into different profiles, suggesting expert, anomaly, learning, and struggling students, based on counterintuitive features (IncorrectSub and Scores) that are not straightforward and thus difficult to explain and understand by the stakeholders (instructors and students) from the explainability algorithm. We further investigated the effects of different feature values on students’ problem-solving behaviors and performance later in the semester to better understand the characteristics of different profiles.
The first feature we look into is the logical errors in student submissions. Tracing patterns of student errors over time can help to effectively understand student misconceptions and struggles in student programs (Ettles et al., 2018). To extract logical errors from incorrect student submissions, we utilize a state-of-the-art code representational model Subtree-based Attention Neural Network (SANN) (Hoq et al., 2023, Hoq et al., 2024, Hoq et al., 2025). SANN is an interpretable code representational model that can encode programs into condensed vector forms based on substructures extracted from codes’ abstract syntax trees. These vectors can be used in various prediction tasks. An attention network identifies the most important subtrees of a program according to a prediction task. We employ a modified version of SANN to predict the correctness of the student code (0: incorrect, 1: correct) and to identify important substructures of the code that are responsible for the prediction, representing logical errors in incorrect codes (Hoq et al., 2024). The original version of SANN uses an optimization approach to identify the best strategy for chunking an Abstract Syntax Tree (AST) into its substructures with regard to a prediction task. Here, we use a modified version of SANN where all of the possible substructures are included in the embedding and training process. This enables us to capture logical errors of various granularity. A normalization layer is included in the attention network before a softmax function to prevent the model from assigning most of the attention to only one logical error in an incorrect code if there are multiple ones. The reason behind such a decision is that for large attention values, the dot products to calculate the attention values can grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients (Vaswani et al., 2017).
For training purposes, we divide the dataset into 80% training, 10% validation, and 10% testing sets. We set the embedding size to 128, optimizer to adamax, and epoch to 50. The accuracy of predicting correct vs incorrect code on the test dataset using all 50 programming problems from all 5 assignments is 88%. Utilizing the attention network, we extract all the logical errors from the incorrect student code.
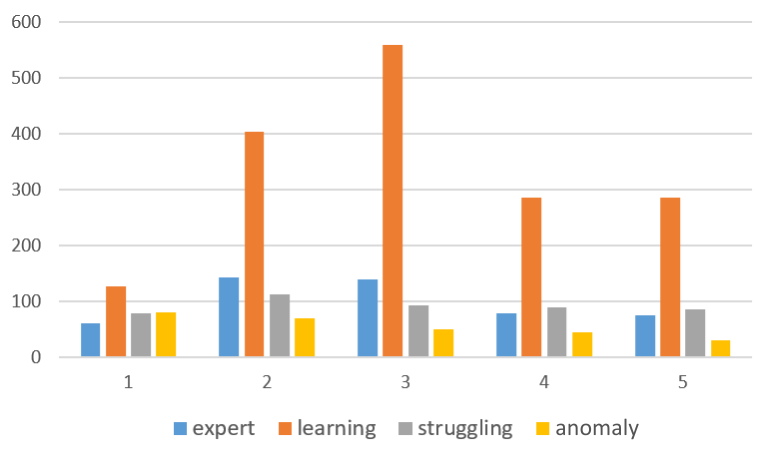
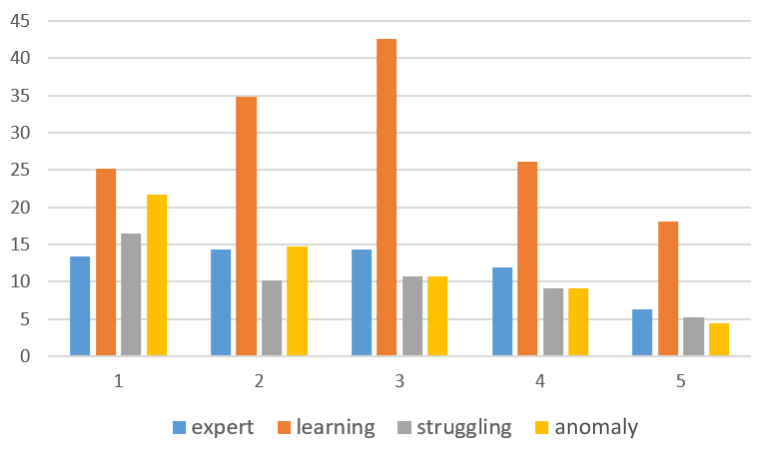
Figure 9 illustrates students’ average number of logical errors in each of the four profiles (experts, anomaly, learning, and struggling) and across the five assignments. These profiles were named with the suggestions of expert CS educators by seeing the characteristics of the profiles, such as expert students showing proficiency in solving problems with background knowledge, anomaly students showing suspicious submission patterns and counter-intuitive final exam performance, learning students showing gradual improvement by trial and error, and struggling students showing reluctance in problem-solving, ending in poor performance in the course. The average number of errors per assignment can provide valuable insights into the complexity and difficulty of each assignment, as well as trends in student effort. Analyzing errors per submission might not reveal these insights, as errors per submission could appear similar for introductory problems. For example, consider a student who makes 12 errors over 4 incorrect submissions before getting the correct answer, compared to a student who makes 3 errors in a single submission and then gets it correct on the second attempt. Both scenarios result in an average of 3 errors per submission but reflect different levels of struggle and persistence. The total number of errors per assignment, however, highlights the overall effort and difficulties students face, providing a clearer picture of their learning process and the challenges posed by each assignment.
Analyzing the number of logical errors reveals that the third assignment is the most challenging, with the highest number of errors, while the first assignment is the easiest, with the fewest errors (Effenberger et al., 2019). Additionally, we observe that the average number of logical errors for the learning profile is the highest among all the profiles. This supports our previous hypothesis that learning students try to learn from failures and trials with a high number of incorrect submissions but show persistence through a high number of attempts and completed assignments. Additionally, the average number of logical errors is comparatively lower for easier assignments. The opposite is seen in the case of struggling students, where no significant changes are observed in the average number of logical errors between assignments with different difficulty levels. A low average number of logical errors is observed in both difficult and easy assignments, with a low number of attempts, suggesting minimal effort throughout the semester. This indicates that they are not trying to solve the problems and might be indifferent to learning in the course. The expert and anomaly students show the least number of logical errors. The expert students’ average number of logical errors goes up and down based on the difficulty level of the assignments, i.e., lowest for the first assignment (easiest one) and highest for the 3rd assignment (most difficult one). However, anomaly students do not show this trend. They have the highest average number of logical errors in the first one as they start the course. However, as time passes, the average number of logical errors decreases with each new assignment. This might suggest a reluctance to solve it independently. We also looked into the average number of submissions for the expert students and anomaly students over the course to obtain more behavioral patterns from each category. We see that the students in the anomaly profile have a reduced submission rate from the first assignment to the last assignment of 65%, while the expert students have a reduction rate of 28%. These observations are consistent with our previous understanding of expert students with higher assignment scores and relatively higher incorrect submissions. In contrast, anomaly students might gradually increase copying from others or getting help from external sources without learning (expedient help-seeking) and directly submitting without trials, even in harder assignments. It is also possible that these students are very good in programming but very bad exam takers, resulting in poor final exam grades.
The analyses of different features across five assignments can reveal distinct patterns and characteristics of the profiles. Although expert and anomaly students have the least number of logical errors, anomaly students show a reluctance to problem-solve. Submission rates reveal a significant reduction over time in anomaly students compared to experts, confirming our observation of the final exam grades (low for the anomaly profile and high for the expert profile). Further exploration indicates that learning students actively refine submissions while struggling students show a lower number of compiler errors, a lower amount of edits in the code, and a lower number of correct submissions. These insights highlight the unique characteristics of each profile, guiding targeted interventions for improved educational support.
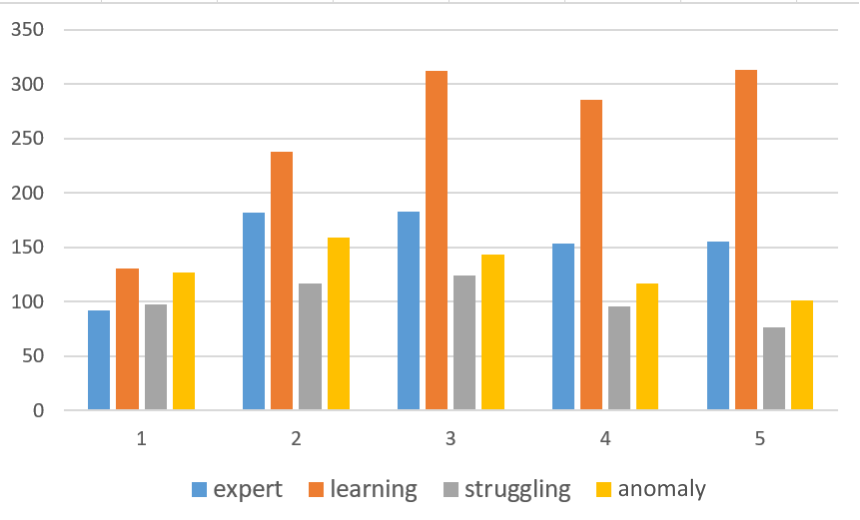
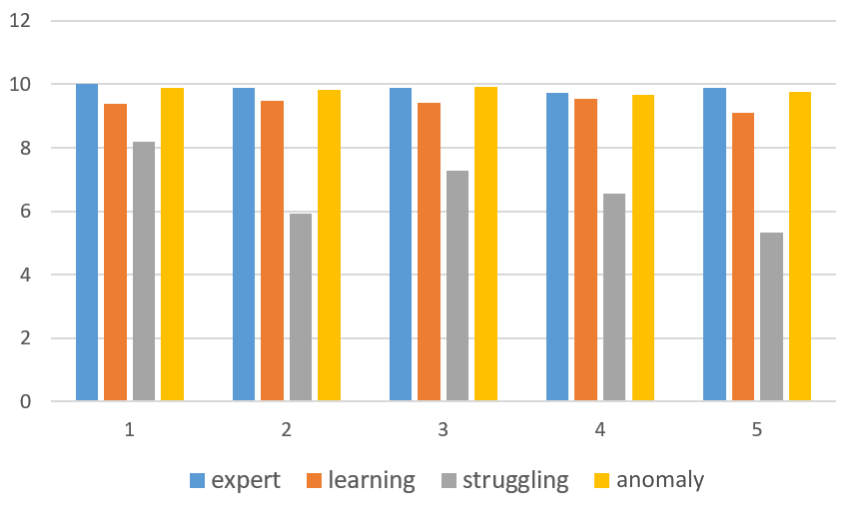
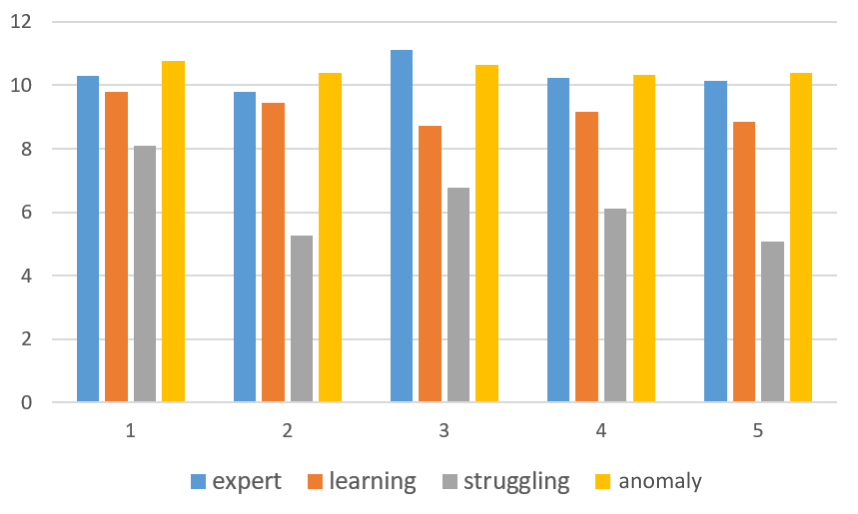
We further analyze other features used in the predictive model to better understand the characteristics of each profile, as shown in Figure 10. This figure illustrates the average number of compiler errors, edit distances, attempts, and correct submissions per student for different profiles for each assignment. Figure 9a shows the average number of compiler errors per student in each assignment from different profiles. The learning students show the highest compiler errors. Both learning and expert students show the highest compiler errors for the most difficult assignments (assignment 2 and assignment 3). However, anomaly students exhibit a different pattern, with the highest number of compiler errors in the easiest assignment (assignment 1), which gradually decreases in the later assignments. The struggling students also exhibit a similar pattern, possibly indicating less effort in these assignments. In Figure 9b, we observe a similar trend with the average edit distance, representing the average number of changes in subsequent submissions by students from each profile. Here, learning students show the characteristic of making the highest edits and changes in the submissions over time, suggesting their trial effort. Figure 9c and Figure 9d illustrate the average number of problems attempted and the average number of problems correctly solved from each assignment, respectively. Struggling students show the least number of attempted problems and correct submissions made in the course. This suggests that these students need intervention and special attention during the course.
5.6. Profiles during early prediction
We replicate our investigation for profiles obtained in early predictions of the final exam score (considering one to four assignments). We get similar importance of the features from SHAP, where assignment scores and the number of incorrect submissions are the two counterintuitive features that cannot be easily understood. Therefore, we obtain the student profiles using these two features as before. Table 6 shows the mean predicted final exam grades of different profiles during the different stages of the early prediction. Notably, the results align with our earlier explorations of these profiles, showcasing consistency in the observed patterns.
As more assignments are considered in the prediction model, the mean grades of the profiles approach closer to the mean grades considering all the assignments. Thus, the misprofiling of students gets reduced (especially after the first 3 assignments). When focusing on the first two assignments, there is a slight discrepancy for learning students, with the mean grade of the learning students being equal to the overall mean grade of 0.64. This is possibly due to their initial trial-and-error learning approach, resembling characteristics of struggling students. However, as the prediction includes more assignments, particularly after the third assignment, the mean exam grades for learning students converge to the actual final grades. Further investigation into early predictions reveals that, when predictions are made based on the first two assignments, some struggling students are misclassified as learning ones. Despite these, the profiles exhibit consistency in their predicted grades, emphasizing the robustness of the model even in the early stages of prediction. These findings demonstrate the importance of considering an ordered comprehensive set of assignments for more accurate early predictions, even without specific deadlines to submit, providing valuable insights into students’ evolving performance trajectories. We further verify this by using the assignments in the reverse order to predict the final exam grades. The results suggest that if we consider the last assignment as the first one and move backward in assignment order, the model’s predictive power increases by 20% compared to the original order of assignments (Table 4) in terms of RMSE and \(\mathrm {R^2}\).
The experimental results suggest that our stacked ensemble model can effectively predict students’ final exam grades using their programming assignment information only with an RMSE of 0.151 and an \(\mathrm {R^2}\) score of 0.55, outperforming other baseline models. It is capable of predicting student performance based on all the course assignments as well as a set of initial assignments for the semester. The results from incorporating the SHAP model can shed light on students’ problem-solving strategies and the connection between those strategies and students’ learning outcomes. Furthermore, student profiling based on counterintuitive features that are not comprehensible from the SHAP outputs can help instructors and students understand the model predictions better.
| Assignment subsets | Expert | Anomaly | Learning | Struggling |
|---|---|---|---|---|
| first 1 assignment | 0.79 | 0.43 | 0.64 | 0.58 |
| first 2 assignments | 0.79 | 0.44 | 0.64 | 0.58 |
| first 3 assignments | 0.78 | 0.45 | 0.7 | 0.59 |
| first 4 assignments | 0.78 | 0.46 | 0.71 | 0.59 |
| all (5) assignments | 0.80 | 0.48 | 0.72 | 0.60 |
6. Discussion
The continuous growth of introductory programming courses, coupled with their inherent complexity (Sahami and Piech, 2016), underscores the critical need for automated tools that empower instructors to deliver timely pedagogical support to students. Constructing predictive models capable of discerning students’ performance and analyzing their problem-solving behaviors is imperative. However, predicting student performance, especially final exam grades, solely based on programming data in introductory programming courses poses a formidable challenge. The distinct nature of final exams that might diverge from hands-on programming assignments complicates the predictive task. Previous research on explainable models predominantly relied on conventional classroom exam data, such as tests, exams, and multiple-choice grades, to predict final exam outcomes. Conversely, incorporating programming features has demonstrated enhanced predictive power in computer science courses (Pereira et al., 2021).
While interim exam grades could potentially augment predictive power, their accessibility for CSEDM models may be hindered by data privacy constraints. Moreover, variations in the outlines and grading mechanisms of different introductory programming classes pose challenges to model generalizability. Notably, programming assignments emerge as a ubiquitous component across diverse courses, forming the basis for our model’s adaptability. Consequently, our model transcends course-specific nuances, making it applicable to any introductory programming curriculum. A salient strength of our model lies in its proficiency in early predictions based on initial assignments, facilitating timely interventions by instructors. Our dataset did not allow for early prediction of students’ performance on a time basis, such as after the first week or month of the course, as the assignments did not have any specific deadline to submit. However, we trained our model with subsets of ordered assignments to test the early prediction power of our model in courses where assignments might not have any specific deadlines or submission time. By doing this, whenever the assignments are due in a course, we can still make early predictions. The results suggest that our model outperformed other baselines significantly with fewer numbers of assignments. This proactive approach is instrumental in providing effective support to struggling students, addressing their needs before potential issues escalate. The necessity of early prediction becomes paramount in ensuring timely assistance, preventing potential setbacks that may arise later in the course.
In the context of ensemble models, overfitting is a significant concern that can undermine the validity of predictions. As highlighted by Hosseini et al. (2020), unexpected overfitting poses a threat to the robustness of complex models. To mitigate this risk, we employed repeated K-fold cross-validation with 10 folds and 10 repeats, ensuring a comprehensive assessment of the model’s performance across different data subsets. Cross-validation might also be vulnerable to overfitting. However, it occurs rarely (Ng et al., 1997). Additionally, hyperparameter tuning was utilized during model fitting to prevent overfitting by keeping the model neither too simple nor too complex. We also ensured diversity in our base models, reducing the likelihood of the ensemble overfitting to specific patterns in the training data.
Integrating our approach in a classroom can offer valuable benefits to both students and instructors. The explainable stacked ensemble model developed in this study can help identify struggling students by predicting their final exam grades based on their programming assignment data. By identifying struggling students, instructors can offer targeted interventions and support to help them improve their learning outcomes. Second, the explanations of the model’s predictions using the SHAP algorithm can help students and instructors understand the model’s decision-making process. This understanding can help build trust in the model’s predictions. Additionally, the study’s interpretation of the SHAP results as profiles that group students based on their problem-solving strategy patterns can provide valuable insights into students’ problem-solving behavior and learning outcomes (Gitinabard et al., 2019, Loginova and Benoit, 2021). This information can help instructors develop personalized teaching strategies that cater to each group’s unique needs, thus enabling more effective interventions and support (Boubekki et al., 2018, Mouri et al., 2018, Sheshadri et al., 2018).
With the profiling of students, we tried to identify different student profiles based on their problem-solving characteristics. Previous studies demonstrated student profiling based on student behaviors (Akram et al., 2019, Boroujeni and Dillenbourg, 2018, Lorenzen et al., 2018, Loginova and Benoit, 2021, Henry and Dumas, 2020). In this study, different student profiles with different distributions were demonstrated to explain the SHAP interpretations where the SHAP results were not straightforward and transparent enough for stakeholders, such as educators and students, to understand parts of the model predictions and make the model more trustworthy. Additionally, an in-depth exploration of these identified profiles was undertaken to understand the distinguishing characteristics of students within each category. This investigation encompassed an examination of coding patterns, including logical and syntactical errors, submission attempts, correct attempts, and the number of alterations in subsequent submissions across various assignments throughout the semester. Notably, unique patterns emerged for each profile, aligning with our hypothesized explanations for the performance outcomes of students, i.e., experts, anomalies, learners, and strugglers. Intriguingly, these patterns offered insights into instances where SHAP struggled to provide adequate explanations for predictions related to final exam performance. Furthermore, we extended our analysis when the model was making early predictions and observed the consistency of the profiles over time.
These profiles were named with the help of expert educators of CS Education to understand the characteristics better. We analyzed and showed different patterns and trends in these profiles to understand successful students and struggling students in the course. Though these profiles are not direct predictions, we see that students from anomaly and struggling profiles struggle in the final exam, and they also show some distinct patterns over the course time in their problem submissions. These students might be facing problems in understanding different concepts, struggling with programming, cheating from others, taking expedient help, or might even have exam anxieties. Therefore, this profiling technique can act as an alarm system and help instructors understand the characteristics of these students so that they can devise strategies to help them earlier in the course before it is too late. Effective and timely intervention, attention, and help can enable a better learning environment for these students to succeed in the course (Mao, 2019, Veerasamy et al., 2020, Boubekki et al., 2018, Lu et al., 2017).
7. Limitations
There are a few limitations in this work. First, students in this course had no timeline, deadline, or specific order to submit the assignments. Our analysis showed that 95% of the students followed a specific order in submitting the assignments but without a specific deadline. However, we trained our model with subsets of ordered assignments to test the generalizability of the model in courses where fewer assignments are available. This might introduce some bias in the model as for the remaining 5% of the students (who submitted the assignments in a different order), the first assignment we considered might be one of the last assignments of the semester. Additionally, the dataset used in this study has potential plagiarism issues. Plagiarism affects the performance of our model because programming submission information and problem-solving patterns do not convey the actual information about the cheating students’ learning.
The dataset lacks sufficient contextual information related to the course and the CodeWorkout implementation. We do not know whether the platform was mandatory for the students in that course and whether the assignments from this platform were counted toward the grades. There is no information about the nature of the final exam and the grading rubric as well. Moreover, there is no information on dropped-out students or students who missed the final exam. The final exam grades of these students (less than 1% of the dataset) are stated as zero, which might affect the performance of a predictive model.
Additionally, student profiling was used in this study to analyze the SHAP values and counterintuitive feature impacts on predictions. This aims to make the model more trustworthy than using only the SHAP outputs that are not easily comprehensible by instructors and students. Nonetheless, more components might arise for a more complex student body in a classroom setting where more than two components can be considered. In that case, more student profiles will emerge in the interpretation process based on the feature interactions. We intend to explore more complex situations and analyze the explanations obtained from SHAP with more granular student profiles in the future.
Furthermore, the generalizability of our model to other courses with different structures and fewer assignments remains untested. While we attempted to address this by training the model on subsets of ordered assignments, this does not fully capture the diversity of potential course designs and student behaviors. Future research should explore the model’s applicability across various educational settings and incorporate more detailed contextual and behavioral data to enhance its robustness and accuracy.
Finally, our study did not account for potential confounding factors such as students’ prior knowledge, learning styles, or external support mechanisms, which could influence their performance and engagement with the programming assignments. Including such variables in future studies could provide a more comprehensive understanding of the factors driving student success and improve the model’s predictive capabilities.
8. Conclusion
In this study, we extracted important data-driven features from student programming submissions that can be representative of student problem-solving behavior and utilized them to predict students’ performance. Furthermore, we developed an explainable stacked ensemble model that can predict student final exam grades from their programming assignment information, even from the first few assignments of the course, to make early predictions and facilitate effective intervention in a timely manner. Our model could significantly outperform baseline models, including Linear regression, KNN, SVM, XGBoost, Bagging, and Boosting. The predictions made by our model were explained using the SHAP algorithm, which shows the importance and direction of impacts for each feature with regard to the predictions. We have provided explanations of the decisions made by the model at two levels: explanations of the decision for a student at an individual level and explanations of the overall predictions at a global level. This explanation can help students and instructors understand the model’s predictions and make it trustworthy. We used a combination of descriptive statistical analysis and mixture models to interpret the SHAP results as profiles that group students based on their problem-solving strategy patterns. We further investigated the consistency of these profiles using different student programming features to understand the characteristics better. This enables us to gain insights into students’ problem-solving behavior and connection to their learning outcomes.
9. Future Work
In the future, we intend to utilize our model for early prediction by training it on a dataset where students’ attempts at assignments follow a specified deadline. This will facilitate instructors’ intervention and help students on a timely basis, such as within the first few weeks of the semester. Moreover, we want to investigate student problem-solving strategies for individual assignments that can help to understand their struggles in assignments with specific programming concepts, such as loop structures or conditional statements. In this study, student profiling was used by discretizing the students into two components (low and high) based on each feature value to analyze the SHAP values where feature impact on the predictions was not straightforward and counterintuitive. However, if we consider more than two components for each feature for a more complex student body, more student profiles might emerge in the interpretation process based on the feature interactions. We intend to explore more complex situations and analyze explanations obtained from SHAP with more granular student profiles in the future. Furthermore, we intend to conduct in-depth studies to detect plagiarism and cheating in students’ programming codes. This includes strategies for similarity analysis and anomaly detection. For instance, we can assess the similarity between two codes through program embedding approaches where the structural information of each program is captured through vectors. Moreover, we can analyze students’ normalized submission rate distributions to identify odd patterns for a particular assignment and gain insights into the likelihood of students requiring attention and intervention.
Acknowledgements
This research was partially supported by the National Science Foundation (NSF) under Grants #2426837 and #2426839. Any opinions, findings, and conclusions expressed in this material are those of the authors and do not necessarily reflect the views of NSF. This paper is an extension of an earlier paper by the same authors presented at the EDM 2023 conference: Hoq et al. 2023.
References
- Afzaal, M., Nouri, J., Zia, A., Papapetrou, P., Fors, U., Wu, Y., Li, X., and Weegar, R. 2021. Explainable ai for data-driven feedback and intelligent action recommendations to support students self-regulation. Frontiers in Artificial Intelligence 4, 723447.
- Ahadi, A., Lister, R., Haapala, H., and Vihavainen, A. 2015. Exploring machine learning methods to automatically identify students in need of assistance. In Proceedings of the 11th Annual International Conference on International Computing Education Research. Association for Computing Machinery, Omaha, Nebraska, USA, 121–130.
- Ahmed, I., Jeon, G., and Piccialli, F. 2022. From artificial intelligence to explainable artificial intelligence in industry 4.0: a survey on what, how, and where. IEEE Transactions on Industrial Informatics 18, 8, 5031–5042.
- Akram, B., Min, W., Wiebe, E., Mott, B., Boyer, K. E., and Lester, J. 2018. Improving stealth assessment in game-based learning with lstm-based analytics. In Proceedings of the 11th International Conference on Educational Data Mining (EDM), K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, Buffalo, NY, USA, 208–218.
- Akram, B., Min, W., Wiebe, E., Mott, B., Boyer, K. E., and Lester, J. 2019. Assessing middle school students’ computational thinking through programming trajectory analysis. In Proceedings of the 50th ACM Technical Symposium on Computer Science Education (SIGCSE). Association for Computing Machinery, Minneapolis, MN, USA, 1269–1269.
- Alam, N., Acosta, H., Gao, K., and Mostafavi, B. 2022. Early prediction of student
performance in a programming class using prior code submissions and metadata. In Proceedings
of the 6th Educational Data Mining in Computer Science Education (CSEDM) Workshop,
B. Akram, T. W. Price, Y. Shi, P. Brusilovsky, and S. I. Han Hsiao, Eds. Durham, UK, 30–39.
https://doi.org/10.5281/zenodo.6983408. - Alon, U., Zilberstein, M., Levy, O., and Yahav, E. 2019. code2vec: Learning distributed representations of code. Proceedings of the ACM on Programming Languages 3, POPL, 1–29.
- Baranyi, M., Nagy, M., and Molontay, R. 2020. Interpretable deep learning for university dropout prediction. In Proceedings of the 21st Annual Conference on Information Technology Education. Association for Computing Machinery, Virtual, 13–19.
- Boroujeni, M. S. and Dillenbourg, P. 2018. Discovery and temporal analysis of latent study patterns in mooc interaction sequences. In Proceedings of the 8th International Conference on Learning Analytics and Knowledge. Association for Computing Machinery, Sydney, Australia, 206–215.
- Boubekki, A., Jain, S., and Brefeld, U. 2018. Mining user trajectories in electronic text books. In Proceedings of the 11th International Conference on Educational Data Mining (EDM), K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, Buffalo, NY, USA, 147–156.
- Carter, A., Hundhausen, C., and Olivares, D. 2019. Leveraging the Integrated Development Environment for Learning Analytics. Cambridge University Press, 679–706.
- Castro-Wunsch, K., Ahadi, A., and Petersen, A. 2017. Evaluating neural networks as a method for identifying students in need of assistance. In Proceedings of the ACM Technical Symposium on Computer Science Education (SIGCSE). Association for Computing Machinery, Seattle, WA, US, 111–116.
- Chen, H.-C., Prasetyo, E., Tseng, S.-S., Putra, K. T., Kusumawardani, S. S., and Weng, C.-E. 2022. Week-wise student performance early prediction in virtual learning environment using a deep explainable artificial intelligence. Applied Sciences 12, 4, 1885.
- Costa, E. B., Fonseca, B., Santana, M. A., de Araújo, F. F., and Rego, J. 2017. Evaluating the effectiveness of educational data mining techniques for early prediction of students’ academic failure in introductory programming courses. Computers in Human Behavior 73, C, 247–256.
- de Raadt, M., Hamilton, M., Lister, R., Tutty, J., Baker, B., Box, I., Cutts, Q., Fincher, S., Hamer, J., Haden, P., et al. 2005. Approaches to learning in computer programming students and their effect on success. In Proceedings of the 28th Annual Conference of the Higher Education Research and Development Society of Australasia. Higher Education in a Changing World, M. Weisz and Smith, Eds. Higher Education Research & Development Society of Australia, Sydney, Australia, 408–414.
- Edwards, S. H. and Murali, K. P. 2017. Codeworkout: short programming exercises with built-in data collection. In Proceedings of the 2017 ACM Conference on Innovation and Technology in Computer Science Education. Association for Computing Machinery, Bologna, Italy, 188–193.
- Edwards, S. H., Snyder, J., Pérez-Quiñones, M. A., Allevato, A., Kim, D., and Tretola, B. 2009. Comparing effective and ineffective behaviors of student programmers. In Proceedings of the 5th International Workshop on Computing Education Research Workshop. Association for Computing Machinery, Berkeley, CA, USA, 3–14.
- Effenberger, T., Cechák, J., and Pelánek, R. 2019. Difficulty and
complexity of introductory programming problems. In Proceedings of the
Educational Data Mining in Computer Science Education Workshop, D. Azcona,
Y. V. Paredes, S. I.-H. Hsiao, and T. Price, Eds. Tempe, AZ, USA, –.
https://www.fi.muni.cz/˜xpelanek/publications/difficulty-complexity-programming.pdf. - Embarak, O. 2021. Explainable artificial intelligence for services exchange in smart cities. In Explainable Artificial Intelligence for Smart Cities, M. Lahby, U. Kose, and A. K. Bhoi, Eds. Vol. 1. Taylor & Francis, Boca Raton, 13–30.
- Estey, A. and Coady, Y. 2016. Can interaction patterns with supplemental study tools predict outcomes in cs1? In Proceedings of the ACM Conference on Innovation and Technology in Computer Science Education. Association for Computing Machinery, Arequipa, Peru, 236–241.
- Ettles, A., Luxton-Reilly, A., and Denny, P. 2018. Common logic errors made by novice programmers. In Proceedings of the 20th Australasian Computing Education Conference. Association for Computing Machinery, Brisbane, Queensland, Australia, 83–89.
- Gitinabard, N., Heckman, S., Barnes, T., and Lynch, C. F. 2019. What will you do next? a sequence analysis on the student transitions between online platforms in blended courses. In Proceedings of the 12th International Conference on Educational Data Mining (EDM), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, Montréal, Canada, 59–68.
- Hasib, K. M., Rahman, F., Hasnat, R., and Alam, M. G. R. 2022. A machine learning and explainable ai approach for predicting secondary school student performance. In Proceedings of the 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC). IEEE, Virtual, 0399–0405.
- Henry, J. and Dumas, B. 2020. Developing an assessment to profile students based on their understanding of the variable programming concept. In Proceedings of the 2020 ACM Conference on Innovation and Technology in Computer Science Education. Association for Computing Machinery, Trondheim, Norway, 33–39.
- Hoq, M., Brusilovsky, P., and Akram, B. 2023. Analysis of an explainable student performance prediction model in an introductory programming course. In Proceedings of the 16th International Conference on Educational Data Mining (EDM), M. Feng, T. Käser, and P. Talukdar, Eds. International Educational Data Mining Society, Bengaluru, India, 79–90.
- Hoq, M., Chilla, S. R., Ahmadi Ranjbar, M., Brusilovsky, P., and Akram, B. 2023. Sann: Programming code representation using attention neural network with optimized subtree extraction. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management. Association for Computing Machinery, Birmingham, UK, 783–792.
- Hoq, M., Patil, A., Akhuseyinoglu, K., Brusilovsky, P., and Akram, B. 2025. An automated approach to recommending relevant worked examples for programming problems. In Proceedings of the 56th ACM Technical Symposium on Computer Science Education (SIGCSE) V. 1. Association for Computing Machinery, Pittsburgh, PA, USA, –. (To be appeared).
- Hoq, M., Shi, Y., Leinonen, J., Babalola, D., Lynch, C., Price, T., and Akram, B. 2024. Detecting chatgpt-generated code submissions in a cs1 course using machine learning models. In Proceedings of the 55th ACM Technical Symposium on Computer Science Education (SIGCSE) V. 1. Association for Computing Machinery, Portland, OR, USA, 526–532.
- Hoq, M., Vandenberg, J., Mott, B., Lester, J., Norouzi, N., and Akram, B. 2024. Towards attention-based automatic misconception identification in introductory programming courses. In Proceedings of the 55th ACM Technical Symposium on Computer Science Education (SIGCSE) V. 2. Association for Computing Machinery, Portland, OR, USA, 1680–1681.
- Hosseini, M., Powell, M., Collins, J., Callahan-Flintoft, C., Jones, W., Bowman, H., and Wyble, B. 2020. I tried a bunch of things: The dangers of unexpected overfitting in classification of brain data. Neuroscience & Biobehavioral Reviews 119, 456–467.
- Ihantola, P., Vihavainen, A., Ahadi, A., Butler, M., Börstler, J., Edwards, S. H., Isohanni, E., Korhonen, A., Petersen, A., Rivers, K., et al. 2015. Educational data mining and learning analytics in programming: Literature review and case studies. In Proceedings of the 2015 ITiCSE on Working Group Reports. Association for Computing Machinery, Vilnius, Lithuania, 41–63.
- Jadud, M. C. 2006. Methods and tools for exploring novice compilation behaviour. In Proceedings of the 2nd International Workshop on Computing Education Research. Association for Computing Machinery, Canterbury, UK, 73–84.
- Jamjoom, M., Alabdulkreem, E., Hadjouni, M., Karim, F., and Qarh, M. 2021. Early prediction for at-risk students in an introductory programming course based on student self-efficacy. Informatica 45, 6, 1–9.
- Joseph, A. 2019. Shapley regressions: A framework for statistical inference on machine learning models. arXiv preprint arXiv:1903.04209.
- Kamal, M. S., Northcote, A., Chowdhury, L., Dey, N., Crespo, R. G., and Herrera-Viedma, E. 2021. Alzheimer’s patient analysis using image and gene expression data and explainable-ai to present associated genes. IEEE Transactions on Instrumentation and Measurement 70, 1–7.
- Karimi, H., Derr, T., Huang, J., and Tang, J. 2020. Online academic course performance prediction using relational graph convolutional neural network. In Proceedings of the 13th International Conference on Educational Data Mining (EDM), A. N. Rafferty, J. Whitehill, C. Romero, and V. Cavalli-Sforza, Eds. International Educational Data Mining Society, –, 444–450.
- Khan, I., Al Sadiri, A., Ahmad, A. R., and Jabeur, N. 2019. Tracking student performance in introductory programming by means of machine learning. In Proceedings of the 4th MEC International Conference on Big Data and Smart City (ICBDSC). IEEE, Muscat, Oman, 1–6.
- Lauría, E. J., Baron, J. D., Devireddy, M., Sundararaju, V., and Jayaprakash, S. M. 2012. Mining academic data to improve college student retention: An open source perspective. In Proceedings of the 2nd International Conference on Learning Analytics and Knowledge. Association for Computing Machinery, Vancouver, British Columbia, Canada, 139–142.
- Liu, E., Koprinska, I., and Yacef, K. 2023. Early prediction of student performance in online programming courses. In Proceedings of the 24th International Conference on Artificial Intelligence in Education (AIED), N. Wang, G. Rebolledo-Mendez, N. Matsuda, O. C. Santos, and V. Dimitrova, Eds. Springer, Springer Nature Switzerland, Tokyo, Japan, 365–371.
- Llanos, J., Bucheli, V. A., and Restrepo-Calle, F. 2023. Early prediction of student performance in cs1 programming courses. PeerJ Computer Science 9, e1655.
- Loginova, E. and Benoit, D. F. 2021. Embedding navigation patterns for student performance prediction. In Proceedings of the 14th International Conference on Educational Data Mining (EDM), S. S. Hsiao, I-Han (Sharon)and Sahebi, F. Bouchet, and J.-J. Vie, Eds. International Educational Data Mining Society, Virtual, 391–399.
- Lorenzen, S., Hjuler, N., and Alstrup, S. 2018. Tracking behavioral patterns among students in an online educational system. In Proceedings of the 11th International Conference on Educational Data Mining (EDM), K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, Buffalo, NY, USA, 280–285.
- Lu, O. H., Huang, J. C., Huang, A. Y., and Yang, S. J. 2017. Applying learning analytics for improving students engagement and learning outcomes in an moocs enabled collaborative programming course. Interactive Learning Environments 25, 2, 220–234.
- Lu, Y., Wang, D., Meng, Q., and Chen, P. 2020. Towards interpretable deep learning models for knowledge tracing. In Proceedings of the 21st International Conference on Artificial Intelligence in Education (AIED), I. I. Bittencourt, M. Cukurova, K. Muldner, R. Luckin, and E. Millán, Eds. Springer International Publishing, Palermo, Italy, 185–190.
- Lundberg, S. M., Erion, G. G., and Lee, S.-I. 2018. Consistent individualized feature attribution for tree ensembles. arXiv preprint arXiv:1802.03888.
- Lundberg, S. M. and Lee, S.-I. 2017. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, U. v. Luxburg, I. Guyon, S. Bengio, H. Wallach, and R. Fergus, Eds. Vol. 30. Curran Associates Inc., Long Beach, CA, USA, 4768–4777.
- Mao, Y. 2019. One minute is enough: Early prediction of student success and event-level difficulty during novice programming tasks. In Proceedings of the 12th International Conference on Educational Data Mining (EDM), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, Montréal, Canada, 119–128.
- Mao, Y., Khoshnevisan, F., Price, T., Barnes, T., and Chi, M. 2022. Cross-lingual adversarial domain adaptation for novice programming. In Proceedings of the AAAI Conference on Artificial Intelligence. AAAI Press, Philadelphia, PA, US, 7682–7690.
- Marsden, J., Yoder, S., and Akram, B. 2022. Predicting Student Performance with Control-flow
Graph Embeddings. In 6th Educational Data Mining in Computer Science Education (CSEDM)
Workshop, B. Akram, T. W. Price, Y. Shi, P. Brusilovsky, and S. I. Han Hsiao, Eds. Durham, UK,
32–40.
https://doi.org/10.5281/zenodo.6983402. - Mouri, K., Shimada, A., Yin, C., and Kaneko, K. 2018. Discovering hidden browsing patterns using non-negative matrix factorization. In Proceedings of the 11th International Conference on Educational Data Mining (EDM), K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, Buffalo, NY, USA, 568–571.
- Mu, T., Jetten, A., and Brunskill, E. 2020. Towards suggesting actionable interventions for wheel-spinning students. In Proceedings of The 13th International Conference on Educational Data Mining (EDM), A. N. Rafferty, J. Whitehill, C. Romero, and V. Cavalli-Sforza, Eds. International Educational Data Mining Society, Virtual, 183–193.
- Muddamsetty, S. M., Jahromi, M. N., and Moeslund, T. B. 2021. Expert level evaluations for explainable ai (xai) methods in the medical domain. In Proceedings of the International Conference on Pattern Recognition, A. Del Bimbo, R. Cucchiara, S. Sclaroff, G. M. Farinella, T. Mei, M. Bertini, H. J. Escalante, and R. Vezzani, Eds. Springer, Springer International Publishing, Virtual, 35–46.
- Ng, A. Y. et al. 1997. Preventing” overfitting” of cross-validation data. In Proceedings of the Fourteenth International Conference on Machine Learning, D. H. Fisher, Ed. Vol. 97. Morgan Kaufmann Publishers Inc., San Francisco, CA, US, 245–253.
- Pei, B. and Xing, W. 2022. An interpretable pipeline for identifying at-risk students. Journal of Educational Computing Research 60, 2, 380–405.
- Pereira, F. D., Fonseca, S. C., Oliveira, E. H., Cristea, A. I., Bellhäuser, H., Rodrigues, L., Oliveira, D. B., Isotani, S., and Carvalho, L. S. 2021. Explaining individual and collective programming students’ behavior by interpreting a black-box predictive model. IEEE Access 9, 117097–117119.
- Pereira, F. D., Oliveira, E., Cristea, A., Fernandes, D., Silva, L., Aguiar, G., Alamri, A., and Alshehri, M. 2019. Early dropout prediction for programming courses supported by online judges. In Proceedings of the 20th International Conference on Artificial Intelligence in Education (AIED), S. Isotani, E. Millán, A. Ogan, P. Hastings, B. McLaren, and R. Luckin, Eds. Springer, Springer International Publishing, Chicago, IL, USA, 67–72.
- Quille, K. and Bergin, S. 2019. Cs1: how will they do? how can we help? a decade of research and practice. Computer Science Education 29, 2-3, 254–282.
- Ribeiro, M. T., Singh, S., and Guestrin, C. 2016. ”why should i trust you?” explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Association for Computing Machinery, San Francisco, CA, USA, 1135–1144.
- Ryan, A. M. and Shim, S. S. 2012. Changes in help seeking from peers during early adolescence: Associations with changes in achievement and perceptions of teachers. Journal of Educational Psychology 104, 4, 1122.
- Sahami, M. and Piech, C. 2016. As cs enrollments grow, are we attracting weaker students? In Proceedings of the 47th ACM Technical Symposium on Computing Science Education (SIGCSE). Association for Computing Machinery, Memphis, TN, US, 54–59.
- Scheers, H. and De Laet, T. 2021. Interactive and explainable advising dashboard opens the black box of student success prediction. In Proceedings of the 16th European Conference on Technology Enhanced Learning (EC-TEL), T. De Laet, R. Klemke, C. Alario-Hoyos, I. Hilliger, and A. Ortega-Arranz, Eds. Springer, Springer International Publishing, Bozen-Bolzano, Italy, 52–66.
- Serradilla, O., Zugasti, E., Cernuda, C., Aranburu, A., de Okariz, J. R., and Zurutuza, U. 2020. Interpreting remaining useful life estimations combining explainable artificial intelligence and domain knowledge in industrial machinery. In Proceedings of the 2020 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE). IEEE, Glasgow, UK, 1–8.
- Shahiri, A. M., Husain, W., et al. 2015. A review on predicting student’s performance using data mining techniques. Procedia Computer Science 72, 414–422.
- Shapley, L. S. 1952. Quota solutions of n-person games. Tech. rep., RAND CORP SANTA MONICA CA.
- Sheard, J., Markham, S., and Dick, M. 2003. Investigating differences in cheating behaviours of it undergraduate and graduate students: The maturity and motivation factors. Higher Education Research & Development 22, 1, 91–108.
- Sheshadri, A., Gitinabard, N., Lynch, C. F., Barnes, T., and Heckman, S. 2018. Predicting student performance based on online study habits: A study of blended courses. In Proceedings of the 11th International Conference on Educational Data Mining (EDM), K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, Buffalo, NY, USA, 87–96.
- Shi, Y., Schmucker, R., Chi, M., Barnes, T., and Price, T. 2023. KC-Finder: Automated knowledge component discovery for programming problems. In Proceedings of the 16th International Conference on Educational Data Mining (EDM), M. Feng, T. Käser, and P. Talukdar, Eds. International Educational Data Mining Society, Bengaluru, India, 28–39.
- Singh, A., Sengupta, S., Rasheed, M. A., Jayakumar, V., and Lakshminarayanan, V. 2021. Uncertainty aware and explainable diagnosis of retinal disease. In Proceedings of the Medical Imaging 2021: Imaging Informatics for Healthcare, Research, and Applications, T. M. Deserno and B. J. Park, Eds. Vol. 11601. SPIE, Virtual, 116–125.
- Sun, Q., Wu, J., and Liu, K. 2020. Toward understanding students’ learning performance in an object-oriented programming course: The perspective of program quality. IEEE Access 8, 37505–37517.
- Sweeney, M., Lester, J., Rangwala, H., Johri, A., et al. 2016. Next-term student performance prediction: A recommender systems approach. Journal of Educational Data Mining 8, 1, 22–51.
- Thakker, D., Mishra, B. K., Abdullatif, A., Mazumdar, S., and Simpson, S. 2020. Explainable artificial intelligence for developing smart cities solutions. Smart Cities 3, 4, 1353–1382.
- Ting, K. M. and Witten, I. H. 1997. Stacked generalization: when does it work? In Poceedings of the 15th International Joint Conference on Artificial Intelligence. IJCAI, Buenos Aires, Argentina, 866–871.
- Trifoni, A. and Shahini, M. 2011. How does exam anxiety affect the performance of university students. Mediterranean Journal of Social Sciences 2, 2, 93–100.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I. 2017. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems, U. v. Luxburg, I. Guyon, S. Bengio, H. Wallach, and R. Fergus, Eds. Curran Associates Inc., Long Beach, CA, USA, 6000–6010.
- Veerasamy, A. K., D’Souza, D., Apiola, M.-V., Laakso, M.-J., and Salakoski, T. 2020. Using early assessment performance as early warning signs to identify at-risk students in programming courses. In Proceedings of the 2020 IEEE Frontiers in Education Conference (FIE). IEEE, Uppsala, Sweden, 1–9.
- Vultureanu-Albişi, A. and Bădică, C. 2021. Improving students’ performance by interpretable explanations using ensemble tree-based approaches. In Proceedings of the 2021 IEEE 15th International Symposium on Applied Computational Intelligence and Informatics (SACI). IEEE, Virtual, 215–220.
- Watson, C. and Li, F. W. 2014. Failure rates in introductory programming revisited. In Proceedings of the 2014 Conference on Innovation & Technology in Computer Science Education. Association for Computing Machinery, Uppsala Sweden, 39–44.
- Wolpert, D. H. 1992. Stacked generalization. Neural Networks 5, 2, 241–259.
- Yoder, S., Hoq, M., Brusilovsky, P., and Akram, B. 2022. Exploring sequential
code embeddings for predicting student success in an introductory programming course.
In 6th Educational Data Mining in Computer Science Education (CSEDM) Workshop,
B. Akram, T. W. Price, Y. Shi, P. Brusilovsky, and S. I. Han Hsiao, Eds. Durham, UK, 2–9.
https://doi.org/10.5281/zenodo.6983195. - Yudelson, M., Hosseini, R., Vihavainen, A., and Brusilovsky, P. 2014. Investigating automated student modeling in a java MOOC. In Proceedings of the 7th International Conference on Educational Data Mining (EDM), K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, London, United Kingdom, 261–264.
- Zhang, J., Wang, X., Zhang, H., Sun, H., Wang, K., and Liu, X. 2019. A novel neural source code representation based on abstract syntax tree. In 2019 IEEE/ACM 41st International Conference on Software Engineering (ICSE). IEEE, Montral, Canada, 783–794.