Abstract
Gaming the system is a persistent problem in Computer-Based Learning Platforms. While substantial progress has been made in identifying and understanding such behaviors, effective interventions remain scarce. This study uses a method of causal moderation known as Fully Latent Principal Stratification to explore the impact of two types of interventions – gamification and manipulation of assistance access – on the learning outcomes of students who tend to game the system. The results indicate that gamification does not consistently mitigate these negative behaviors. One gamified condition had a consistently positive effect on learning regardless of students’ propensity to game the system, whereas the other had a negative effect on gamers. However, delaying access to hints and feedback may have a positive effect on the learning outcomes of those gaming the system. This paper also illustrates the potential for integrating detection and causal methodologies within educational data mining to evaluate effective responses to detected behaviors.Keywords
Abstract
1. Introduction
Gaming the system – attempting to progress through a learning activity without learning (Baker et al., 2008) – is an enduring problem that reduces the efficacy of Computer-Based Learning Platforms (CBLPs). Educational Data Mining (EDM) researchers have made substantial progress in identifying instances of gaming the system behaviors (Paquette et al., 2014, Paquette and Baker, 2017, Paquette and Baker, 2019, Dang and Koedinger, 2019, Baker et al., 2006), and further research has explored the antecedents of these behaviors (Baker et al., 2004, Baker et al., 2008, Baker et al., 2009); however, solutions remain scarce. Although interventions to address gaming the system have been evaluated (Richey et al., 2021, Walonoski and Heffernan, 2006, Murray and VanLehn, 2005, Xia et al., 2020, Baker et al., 2006), most focus on dissuading students from gaming the system instead of improving learning outcomes. Thus, it is unclear which interventions help students who tend to game the system engage with and learn from CBLPs.
This paper explores two types of interventions – gamification and manipulations of access to assistance – which could hypothetically benefit students who tend to game the system. In general, gamification – the act of infusing game features into a system – is seen as a potential method of increasing engagement within CBLPs (Garris et al., 2002, Gaston and Cooper, 2017, Vanacore et al., 2023a). By increasing engagement, gamification could theoretically decrease gaming the system behaviors and help students benefit from the CBLPs. However, features of gamification could exacerbate these behaviors by providing more opportunities to game. Therefore, simpler alternatives may also be effective, such as restricting access to the assistance that is often abused by gamers1 (Murray and VanLehn, 2005). The current research on gaming the system interventions has not fully addressed which interventions are most effective for gamers. Thus, it is unclear what changes in CBLP environments can positively influence these students’ learning behaviors and outcomes.
In this paper, we explore the impact of key differences in learning platforms on students who tend to game the system. More specifically, this study addresses whether students who game the system in a traditional CBLP – one that includes various closed-ended and open-ended questions with immediate hints and feedback – would respond differently to alternative CBLP environments: two gamified CBLPs and a traditional CBLP in which the access to hints and feedback were delayed until the end of each activity. We find that gamification does not consistently mitigate the negative effects of gaming the system on learning, but students who tend to game the system may benefit from delayed hints and feedback.2
As a secondary objective, we present an example of integrating prediction from detection models into causal models. We utilize a method of causal moderation – Fully Latent Principal Stratification (Sales and Pane, 2019)– that can leverage detection model outputs to understand heterogeneity in treatment effects. The combination of detection and causal models provides opportunities to go beyond identifying students’ behaviors and/or latent states (e.g., confusion or knowledge component mastery) to understand how to respond in a way that positively impacts learning.
2. Background
In this section, we provide literature reviews of the relevant aspects of the study. First, we include a review of the suspected antecedents and outcomes associated with gaming behaviors (Section 2.1). Next, we consider the theoretical and empirical support that immediate assistance features (Section 2.2) and gamification (Section 2.3) influence students’ learning-related behaviors and outcomes. Finally, we review research on interventions aimed at mitigating gaming behaviors (Section 2.4).
2.1. Gaming The System
Gaming the system is defined as “attempting to succeed in an educational environment by exploiting properties of the system rather than by learning the material and trying to use that knowledge to answer correctly” (Baker et al., 2008). This definition is operationalized by two key behaviors: rapid and repeated requests for help (hint abuse) and submission of answers in a systemic way (guess-and-check) (Baker et al., 2008, Walonoski and Heffernan, 2006). These behaviors indicate that a student is trying to submit the answers to problems merely to progress through the assignment without deploying the effortful engagement required to learn from the activity.
Therefore, it is not surprising that gaming the system behaviors are correlated with reduced performance within CBLPs (Baker et al., 2004) and poor learning outcomes (Mihaela and Hershkovitz, 2009). Furthermore, gaming is also predictive of low distal outcomes such as state test performance (Pardos et al., 2014) and college enrollment (Adjei et al., 2021). Thus, gaming behaviors may be related to students’ broader educational struggles.
However, gaming the system tends to have a stronger association with student frustration rather than general disengagement (Baker et al., 2008), as it is not correlated with off-task behavior (Baker et al., 2004). Specific program features may cause gaming behaviors by fomenting confusion and frustration (Baker et al., 2009). Research suggests that students move from states of confusion and frustration towards gaming the system behaviors because the CBLP’s features do not adequately address their learning needs (Rodrigo et al., 2008, Baker et al., 2009). When the CBLP’s activities are ambiguous and abstract, students are more likely to game the system (Baker et al., 2009). Thus, it is plausible that decreasing problem difficulty and adding supports to mitigate frustration may reduce gaming (Baker et al., 2008). Alternatively, additional assistance features may dissuade students from persistent and effortful engagement with the content while providing more opportunities to abuse support features.
2.2. On-demand Hints and Immediate Feedback in CBLPs
Although abuse of on-demand hints and immediate feedback are the key characteristics of gaming the system, these are also fundamental features of many CBLPs. Substantial research is dedicated to immediate hints and feedback. Students tend to benefit from timely feedback and support during learning activities (Butler and Woodward, 2018, Shute, 2008, Lu et al., 2023, Razzaq et al., 2007, Lu et al., 2021). Multiple studies present evidence that providing feedback immediately after students respond to or complete problem sets has a positive effect on students’ procedural and conceptual knowledge (Corbett and Anderson, 1994, Dihoff et al., 2003, Phye and Andre, 1989). In many CBLPs, students may also request assistance, which includes hints and feedback as students work on problems. These features have varying implementations. Common hints and feedback methods include presenting general topical information (Aleven and Koedinger, 2000), worked examples that present a complete solution to a similar problem (McLaren et al., 2016), providing the complete solution to the given problem (Williams et al., 2016), being shown similar examples done incorrectly (McLaren et al., 2016, Adams et al., 2014), providing targeted feedback based on a student’s common wrong answer (Gurung et al., 2023, Gurung et al., 2023), and being given a series of step-by-step hints (Feng and Heffernan, 2006).
Overall, these features have differing levels of efficacy. For example, tutoring strategies, which provide problem-specific hints, are effective at improving student performance (Prihar et al., 2021, Patikorn and Heffernan, 2020). Williams et al. (2016) found students performed better when presented with Machine Learning-generated explanations as opposed to only receiving the answer. Research has also shown that feedback is more effective if provided as the student is answering questions than if it is delayed until after an activity (Lu et al., 2023), which supports the argument that assistance should be on-demand and immediate. Yet, there are also implementations of this assistance that show mixed or no efficacy. For example, McLaren et al. (2016) found that worked examples did not improve learning outcomes. Aleven and Koedinger (2000) found that students typically ignored assistance that involved general information aimed at helping students learn concepts; these students preferred hints that focused on the problem on which they were working. Another study found that students required support to utilize on-demand learning assistance but failed to find learning gains even when this support was given (Aleven et al., 2016). Overall, these findings suggest that students want assistance and feedback focused on the problem in which they are struggling; they are less engaged with assistance that provides general information about the concepts they are learning.
In theory, on-demand assistance tutoring strategies in intelligent tutoring systems should encourage help-seeking behaviors, which can increase students’ autonomy and control of their learning (Aleven et al., 2006, Aleven et al., 2016). Yet, students can abuse this control, as exhibited by gaming behaviors. Although there is ample research on the efficacy of hints and feedback, more is needed to understand who benefits from these resources. Furthermore, the interactions between access to these learning supports, how students use these supports, and learning outcomes have not been fully explored.
2.3. Gamification & Engagement
Gamification, adopting features of games into non-game contexts, is a common method of increasing engagement in CBLPs (Landers, 2014, Karagiorgas and Niemann, 2017). Gamification includes incorporating “design elements, game thinking, and game mechanisms” (Karagiorgas and Niemann, 2017). In contrast, game-based learning allows students to engage in learning through a playful activity (Karagiorgas and Niemann, 2017).
According to the Theory of Gamified Learning, gamification impacts students’ learning outcomes by influencing their behaviors as they learn (Landers, 2014). For example, games can influence students’ learning behaviors by turning activities that may be exasperating into ones that are “pleasantly frustrating” (Gee, 2005). This pleasant frustration is often a product of the balance of success and failures necessary for an engaging game (Juul, 2009). It is plausible that a frustrating problem that might cause an uptick in gaming behaviors in a traditional CBLP could produce engagement in a gamified one. As frustration is a likely antecedent of gaming behaviors, gamification could theoretically reduce instances of gaming the system by reframing typically frustrating experiences as enjoyable. This idea is supported by evidence that students respond positively to game-based failure in a gamified learning environment by exhibiting productive performance (Vanacore et al., 2024). Thus, students who might disengage with a traditional CBLP by gaming the system would possibly instead engage with a gamified version of the CBLP; however, the extent to which gamification can produce these “pleasantly frustrating” experiences associated with games is unclear, as engaging with a gamified CBLP is not the same as playing a game. Furthermore, which features of a learning engagement are gamified may be as important as whether a learning experience is gamified at all.
Research on gamification has shown mixed effects on students’ behaviors in learning contexts. Some have found a positive effect of gamified features on student engagement (Garris et al., 2002, Gaston and Cooper, 2017, Vanacore et al., 2023a), while others have not (Malkiewich et al., 2016, McKernan et al., 2015). Garris et al. (2002) found that reward-based systems caused students to take more time and replay problems more frequently. Previous work has also found that gamified performance-based feedback increases students’ persistence behaviors associated with greater impacts on student learning (Vanacore et al., 2023a, Vanacore et al., 2023b). Alternatively, Malkiewich et al. (2016) found that some gamified features, such as narrative elements, did not positively impact students’ persistence within the game. McKernan et al. (2015) also found that reward systems improved students’ perceptions of their experiences, but not their behaviors or outcomes. As gaming the system can be seen as the antithetical behavior of persistence and engagement, it is plausible that gamification could mitigate these behaviors; however, the mixed results suggest that more research is necessary to evaluate this hypothesis.
2.4. Mitigating Gaming the System Behaviors
Interventions for gaming behaviors can be either proactive or reactive. Proactive interventions involve attempting to curtail the gaming behaviors before students have the opportunity to exhibit said behaviors (Aleven et al., 2006, Murray and VanLehn, 2005, Walonoski and Heffernan, 2006, Xia et al., 2020). Reactive options require targeted interventions after the gaming behavior has been identified (Baker et al., 2006).
Research suggests that proactively discouraging students from superfluous hint requests may be an imprecise method of addressing gaming behaviors. Advising students to request hints only when they truly needed them while delaying hint availability by ten seconds reduced hint usage and did not impact overall performance (Murray and VanLehn, 2005). However, Murray and VanLehn (2005) found some evidence that this method may have improved the performance of students who might have otherwise gamed the system; they found a marginally insignificant positive effect on the performance of students with low prior knowledge. The lack of statistical significance may be attributed to the study’s small sample. Thus, the finding suggests that manipulating access to hints could help students who game the system.
Another proactive method includes presenting students with information about their gaming-related behaviors. Researchers have theorized that this intervention may influence students in one of two ways. They make the student aware that the system is logging their behaviors, thus creating “panopticon-like paranoia” of constant awareness of potential observation (Walonoski and Heffernan, 2006). Alternatively, visualizing students’ actions may also nudge students to reflect on their learning behaviors (Xia et al., 2020). Two studies found that providing graphical representations of learning-related behaviors can reduce instances of gaming the system (Walonoski and Heffernan, 2006, Xia et al., 2020). However, neither of these studies evaluated this method’s impact on learning. Furthermore, students who are likely to game the system to progress through learning activities may also game the system to manipulate the outputs of the visualizations.
As a reactive option, Baker et al. (2006) placed students who had previously gamed on specific content into an intervention focused on the content that the students had gamed. In this intervention, students saw an animated dog that displayed emotional responses to their learning-related behaviors. The animation embodied an exaggerated mimic of a teacher’s emotions in response to student behavior (e.g., excitement and positivity if a student exerted effort, or frustration if a student gamed the system). This intervention significantly decreased students’ gaming behaviors and positively affected their learning outcomes, as measured by a post-test, compared to a control group that did not have access to the animated dog.
Overall, there is suggestive evidence that directly dissuading students from gaming behaviors like hint abuse may benefit some students, yet it is unclear whether it has adverse effects on the non-gaming student population. Alternatively, presenting visualizations that represent students’ actions may reduce instances of gaming; however, the learning impact of this method has not been explored. Notably, only the study that imposed a direct content-specific intervention showed a significant impact on learning (Baker et al., 2006). Thus, none of these studies connected the prevention of gaming behaviors with learning outcomes.
One alternative method is to change the learning environment substantially. Richey et al. (2021) evaluated the impact of a gamified CBLP by comparing it to an equivalent non-gamified CBLP and found that the gamified version reduced students’ gaming behaviors, thus improving their learning outcomes. The gamified CBLP included interactive characters that prompted students with feedback and provided “narrative context for why they are performing various problem-solving activities.” The reduction in gaming behavior completely mediated the effects on the posttests, suggesting the gamified elements’ primary mechanism for impacting outcomes is reducing gaming behaviors.
3. Current Study
In the current study, we seek to understand the interplay between gaming the system behaviors, CBLP instructional design, and student learning by evaluating the following research question: Do students who tend to game the system in a traditional CBLP with on-demand hints and immediate feedback (i.e., ’gamers’) benefit from alternative CBLPs?
We address this question using open-source data3 from an efficacy study conducted to evaluate the effects of different CBLPs on middle school students’ (U.S. Grade Seven) algebraic knowledge (Decker-Woodrow et al., 2023). The original study included four conditions (discussed in detail in Section 4.2) consisting of two traditional CBLP conditions administered through ASSISTments and two gamified CBLP conditions (From Here to There! and DragonBox Algebra 12+). In one of the ASSISTments conditions, students worked through traditional problem sets with access to hints and automated immediate feedback (Immediate Condition). In the other ASSISTments condition, access to both hints and feedback was delayed until after students completed problem sets (Delayed Condition). This question was preregistered4 along with the hypotheses that gamers would benefit from both the Delayed Condition condition and gamified conditions relative to the Immediate Condition.
The original efficacy study found that both gamified conditions caused higher performance in algebraic knowledge compared to the delayed condition, but the effect of the Immediate Condition was not significant after controlling for student-level covariates (Decker-Woodrow et al., 2023). The current study is an extension of a previous analysis presented at the 14th International Learning Analytics and Knowledge Conference (Vanacore et al., 2024). In that analysis, we compared the Immediate and Delayed conditions to understand the impact of feedback delivery on learning for students with a higher propensity to game the system in the Immediate Condition. We reported that although students with a low propensity to game the system benefited from the Immediate Condition, those with a high propensity to game the system may have benefited from the Delayed Condition.
Here, we extend this analysis by including gamified conditions to fully explore how differences in CBLP institutional design may produce impact differentials for gamers. These gamified conditions share many key features: dynamic manipulation of equations, performance-based feedback, multiple paths to solutions, and the ability to replay problems. But they also have key differences (further described in Section 4.2), including narrative goals and the way puzzles are used to teach mathematical concepts. The following study does not allow us to understand the effects of individual gamified features, yet we can better understand how different students interact with gamified systems generally and whether these systems have consistent or inconsistent patterns of treatment effect heterogeneity.
4. Method
4.1. Design
This study consists of a randomized controlled trial conducted in a school district in the Southeastern United States. The study consisted of 52 teachers in 10 schools. Students were ranked within classrooms based on their prior state mathematics assessment scores, blocked into sets of five (i.e., quintets), and then randomly assigned into either the From Here to There (FH2T; 40%), DragonBox (20%), Immediate Feedback (20%), or Delayed Feedback (20%) conditions. The disproportionate weighting was intended to allow researchers to focus their work on evaluating and understanding FH2T. The implementation of the study included nine weekly half-hour sessions in which the students worked in their assigned program. A full description of the study design can be found in Decker-Woodrow et al. (2023), an analysis of the study implementation is reported in Vanacore et al. (2024), and a description of the data set can be found in Ottmar et al. (2023).
4.2. Conditions
As explained in Section 3, the study consists of four conditions: two traditional and two gamified CBLPs. Example problems from each condition are presented in Figure 1. All conditions focused on teaching procedural ability, conceptional knowledge, and flexibility in algebraic equation equivalency.
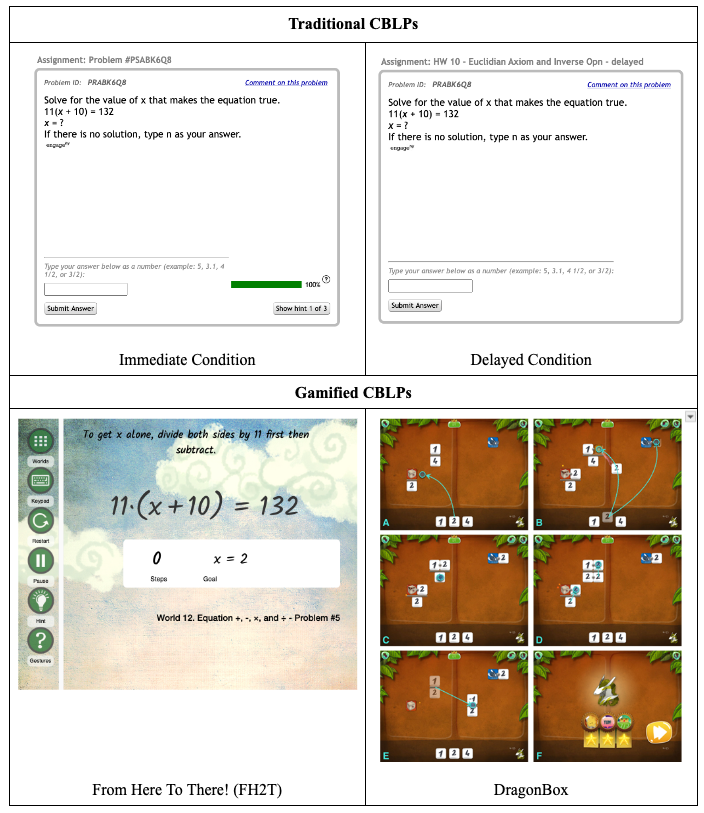
Both traditional problem sets’ conditions (Immediate and Delayed Conditions) were administered through ASSISTments (Heffernan and Heffernan, 2014), an online homework system that assists students as they solve traditional problem sets. The problem sets in ASSISTments are adapted from open-source curricula, thus resembling problems students encounter in their textbooks and homework assignments. ASSISTments presents students with problems one at a time on their screen. Each condition included 218 problems of the same problems selected from three curricula – EngageNY, Utah Math, and Illustrative Math – to address specific algebra skills. The problems were divided into nine problem sets and administered throughout nine half-hour sessions during school hours.
4.2.1. Immediate Hints and Feedback (Immediate Condition)
In the Immediate Condition, students could request hints while solving problems. They also received automatic feedback on whether their answer was correct or incorrect after every submitted answer. Each problem contained a series of hints with a similar structure. The first hint gave the students the first step to answering the problem. The second hint gave the student a worked example of a similar problem. The final hint provided the student with the steps to complete the problem as well as the problem’s solution. Students could submit as many answers as needed but could not move on until they had entered the correct answer. This condition was shown to be effective when implemented as a substitute for paper homework assignments (Roschelle et al., 2016). However, this condition provides both of the features that enable gaming behaviors: a sequence of hints that eventually provide the answer, which students can use for hit abuse, and immediate feedback, which allows for guess-and-check approaches to submitting responses.
4.2.2. Post-Assignment Hints and Feedback (Delayed Condition)
The Delayed Condition provided post-assignment assistance rather than on-demand hints and immediate feedback. In this condition, problem sets were administered in “test mode,” so students did not receive any feedback or hints while submitting answers in each problem set. They could only submit one answer and progressed through the problem set without any feedback on their performance. Students received a report with feedback on their accuracy at the end of each problem set, and they could review their responses, revisit problems, and request hints. This condition was used as an active control in the original study, but we re-conceptualize it here as an intervention for gamers.
4.2.3. From Here to There! (FH2T)
From Here to There! (FH2T) takes a nontraditional approach to algebra instruction by applying aspects of perceptual learning (Goldstone et al., 2010) and embodied cognition (Abrahamson et al., 2020). Instead of presenting students with traditional algebra equations and expressions that students solve or simplify, FH2T gives students access to a starting expression (start state) that they must dynamically transform into a mathematically equivalent expression (goal state). Students can manipulate the expression by dragging numbers and symbols from one position to another on the screen or using a keypad when expanding terms. Only mathematically valid manipulations are accepted. Each valid manipulation counts as a step, which is logged and used to evaluate how efficiently the student transforms the expression from the start to the goal state. FH2T has 252 problems that are presented sequentially by mathematical content and complexity. Students must complete one problem in the sequence before advancing to the next problem.
4.2.4. DragonBox Algebra 12+ (DragonBox)
DragonBox Algebra 12+ 5 (DragonBox) is an educational game that provides instruction in algebraic concepts to secondary school students (ages 12-17). For each problem, students are asked to isolate a box containing a dragon—equivalent to solving an equation for x. This design incorporates research-based pedagogical methods, including discovery-based learning, embedded gestures, diverse representations of concepts, immediate feedback, and adaptive difficulty (Cayton-Hodges et al., 2015, Torres et al., 2016). The game’s key innovation is that students learn the rules of algebra without using or manipulating numbers or traditional algebraic symbols. Thus, students engage with the algebraic concepts as if they are puzzles. Numbers and traditional algebraic symbols are introduced gradually, presumably after the student has learned the underlying concepts. Furthermore, DragonBox applies a narrative goal to the learning: students must allow the dragon to come out of the box by isolating it in the equation. Previous analyses found that DragonBox positively affects engagement and attitudes toward math, but findings are mixed in regard to its efficacy in improving learning outcomes (Siew et al., 2016, Dolonen and Kluge, 2015).
4.3. Analysis Plan
Our goal is to assess whether the students who gamed the system in a traditional CBLP would have benefited from a different CBLP. This poses a methodological difficulty because estimating the effect of randomizing gamers to the Immediate condition requires us to contrast their post-test scores with scores from comparable students in the other conditions; however, we only observe gaming behavior in the Immediate condition. Even if we did observe gaming in another condition, we cannot know if a student who gamed the system in one condition would also game in another. In fact, we hypothesize that students who would game the system in the Immediate Condition would not engage in similar behaviors in the other conditions and benefit from the learning therein.
To address this methodological problem, we propose that students have a baseline propensity to game the system in the Immediate Condition that exists before randomization, regardless of whether it can manifest itself after treatment assignment. Because it is considered a baseline covariate, similar to students’ pretest knowledge, it is independent of the random treatment assignment and can serve as a moderating variable. However, unlike pretest knowledge, only students in the Immediate Condition have the opportunity to display the behavior; therefore, its value in the other conditions is unknown. Nevertheless, once this latent propensity to game the system is estimated, we can evaluate whether it moderates the effects of the various interventions.
Our analysis requires two key steps, which are described in depth below. First, we use a gaming the system detector to identify instances where students are gaming the system within the Immediate Condition. Next, we use the causal method of Fully Latent Principal Stratification (FLPS, (Sales and Pane, 2019)), which will allow us to estimate the effect heterogeneity of each program based on students’ latent propensity to game the system in the Immediate condition. Each of these methods is delineated in the sections below.
4.3.1. Implementation of Gaming The System Detector
This paper employs the rule-based gaming detectors originally created by Paquette et al. (2015) to identify gaming behavior among students working on algebraic problems. To the best of the authors’ knowledge, the Cognitive Model developed by Paquette et al. (2015) was the first detector that was transferable across intelligent tutoring systems, from Cognitive Tutor Algebra (CTA) to ASSISTments. The original rule-based detector was engineered to detect gaming in CTA (Baker et al., 2008). Paquette et al. (2014) further developed the rule-based gaming detector by relying on human judgments through text replays of logged learner actions (Baker et al., 2010). The insights gained from human judgments were used to develop gaming detectors for CTA. Subsequently, the transferability of this rule-based gaming detector was validated in ASSISTments.
We elected to use the rule-based Cognitive Model for identifying gaming behavior as rule-based models mitigate key challenges to more complex detectors: model generalizability and detector rot. Unlike other system-specific gaming detectors, the rule-based model demonstrated cross-system generalizability, underscoring its adaptability and reliability in contexts beyond the original training data set (Paquette et al., 2015). More complex models are also susceptible to detector rot, a phenomenon that refers to the gradual decline in a model’s performance over time. Prior studies have reported that more complex models, using more advanced ML and DL algorithms, are more prone to this phenomenon than their simpler counterparts (Lee et al., 2023, Levin et al., 2022). Given that many gaming the system models were developed years before our study, they are at a higher risk of experiencing detector rot. Consequently, we implemented the rule-based detector, in light of its potential for sustained generalizability and resistance to detector rot.
To implement the rule-based detector for identifying gaming behavior among students, logged student actions are first aggregated into twenty-second clips. These clips are then analyzed alongside additional information to contextualize the actions into more meaningful categories, as outlined in Table 1. This process allows for the identification of specific sequences of action patterns considered indicative of gaming behavior, with a total of 13 patterns detailed in Table 2. For example, analyzing the first pattern, “incorrect → [guess] & [same answer/diff. context] & incorrect” indicates a scenario where the student entered an incorrect answer and re-entered the same incorrect answer within 5 seconds of making the first attempt. For the students in the Immediate Condition in this study, the rule-based detector employs this structured approach, leveraging log-file data compiled in twenty-second intervals (as described in Section 4.4.1) to determine gaming instances during each clip. These determinations are then integrated into the FLPS model, enhancing its ability to accurately reflect student engagement and behavior.
| Identifier | Description
|
|---|---|
| [did not think before help request] | Pause smaller or equal to 5 seconds before a help request |
| [thought before help request] | Pause greater or equal to 6 seconds before a help request |
| [read help messages] | Pause greater or equal to 9 seconds per help message after a help request |
| [scanning help messages] | Pause between 4 and 8 seconds per help message after a help request |
| [searching for bottom-out hint] | Pause smaller or equal to 3 seconds per help message after a help request |
| [thought before attempt] | Pause greater or equal to 6 seconds before step attempt |
| [planned ahead] | Last action was a correct step attempt with a pause greater or equal to 11 seconds |
| [guess] | Pause smaller or equal to 5 seconds before step attempt |
| [unsuccessful but sincere attempt] | Pause greater than or equal to 6 seconds before a bug |
| [guessing with values from problem] | Pause smaller than or equal to 5 seconds before a bug |
| [read error message] | Pause greater than or equal to 9 seconds after a bug |
| [did not read error message] | Pause smaller than or equal to 8 seconds after a bug |
| [thought about error] | Pause greater than or equal to 6 seconds after an incorrect step attempt |
| [same answer/diff. context] | Answer was the same as the previous action, but in a different context |
| [similar answer] | Answer was similar to the previous action (Levenshtein distance of 1 or 2) |
| [switched context before right] | Context of the current action is not the same as the context for the previous |
| (incorrect) action | |
| [same context] | Context of the current action is the same as the previous action |
| [repeated step] | Answer and context are the same as the previous action |
| [diff. answer AND/OR diff. context] | Answer or context is not the same as the previous action |
| Action patterns considered gaming behavior.
|
|---|
| incorrect → [guess] & [same answer/diff. context] & incorrect |
| incorrect → [similar answer] [same context] & incorrect → [similar answer] & [same context] & attempt |
| incorrect → [similar answer] & incorrect → [same answer/diff. context] & attempt |
| [guess] & incorrect → [guess] & [diff. answer AND/OR diff. context] & incorrect → [guess] & [diff. answer AND/OR |
| diff. context & attempt |
| incorrect → [similar answer] & incorrect → [guess] & attempt |
| help & [searching for bottom-out hint] → incorrect → [similar answer] & incorrect |
| incorrect → [same answer/diff. context] & incorrect → [switched context before correct] & attempt/help |
| bug → [same answer/diff. context] & correct → bug |
| incorrect → [similar answer] & incorrect → [switched context before correct] & incorrect |
| incorrect → [switched context before correct] & incorrect → [similar answer] & incorrect |
| incorrect → [similar answer] & incorrect → [did not think before help] & help → incorrect (with first or second answer |
| similar to the last one) |
| help → incorrect → incorrect → incorrect (with at least one similar answer between steps) |
| incorrect → incorrect → incorrect → [did not think before help request] & help (at least one similar answer between steps) |
4.3.2. Estimating Effects Using Fully Latent Principal Stratification
FLPS is a variant of Principal Stratification, a causal inference method used in randomized controlled trials for estimating the intervention effects on subgroups that emerge after the treatment has begun (Frangakis and Rubin, 2002, Page et al., 2015). Generally, to estimate subgroup effects, the subgroups must be defined prior to the intervention and be independent of treatment assignment. For example, to test whether an effect varies based on pretest knowledge, interacting the treatment with the pretest knowledge score estimates how the treatment effect differs across different subgroups of students with similar prior knowledge. However, subgroups identified based on students’ interactions with a treatment program cannot be observed at baseline. Furthermore, they may only be observed for students randomized in some conditions (in the present case, the Immediate Condition). Even if they could be observed in multiple conditions, the student’s behavior is confounded by their condition (i.e., some students may game the system in one condition but would not in another condition). FLPS provides a solution to this methodological problem by modeling these behaviors as manifestations of latent student characteristics, which are not observed for students randomized to some conditions but must be estimated.
Often, a student’s interactions with programs are categorized by a complex series of behaviors. This fact is particularly true in CBLPs, where students may display an array of behaviors during the program, such as meeting implementation goals (Dieter et al., 2020, Vanacore et al., 2024), productive persistence (Vanacore et al., 2023a), mastering knowledge components in mastery learning (Sales and Pane, 2019), and gaming-the-system behaviors that may be viewed as indicators of latent student characteristics (i.e., high fidelity users, persistent learners, mastery users, gamers). Understanding which latent behavioral characteristics are associated with effect heterogeneity can help provide a better understanding of how CBLPs impact students.
However, these latent behavioral characteristics are likely context-dependent (e.g., a student may persist in one CBLP and not another). These behaviors are unobserved for the students randomized to conditions where they do not have the same opportunity to display the relevant behaviors as they did not interact with the same CBLP. For example, some students might request hints in a condition that provides them. However, other conditions may not provide the opportunity to request hints, so we cannot observe whether students in this condition would have requested them. Furthermore, when the relevant behaviors are observable, they are confounded by the students’ assigned conditions, which presumably influence their behaviors. For example, suppose students are randomized between receiving optional hints or explanations. In that case, students who prefer hints may be unlikely to request help when they are randomized to explanations and vice versa. Therefore, their underlying latent student characteristics that define the subgroups in the FLPS can be interpreted as explaining students’ behaviors if randomized to a specific condition.
Sales and Pane (2019) used this method to determine whether the effect of Cognitive Tutor Algebra I on students varies based on whether students were likely to master knowledge components in Cognitive Tutor by estimating the likelihood of mastering knowledge components for the treatment group as a latent variable. In the current study, we evaluate whether the effect of each alternative condition (Delayed Condition, FH2T, DrangonBox) differs based on students’ latent propensity to game the system had they been assigned to Immediate Condition. This propensity to game the system in the Immediate Condition is independent of students’ treatment assignment, as it exists prior to any treatment and regardless of whether it has the opportunity to manifest.
Since students’ gaming behavior was detected in the Immediate Condition, our goal is to know how students with a high propensity to game the system in the immediate condition would fare if placed in each of the other conditions: the Delayed Condition, FH2T, or DragonBox. For simplicity, we refer to the Immediate Condition as the control and each of the other conditions as treatments. We present the following model as if there is only one treatment for simplicity, but the model estimated in this paper includes multiple treatment conditions, and therefore, multiple main and moderating effects.
Let \(\tau _i\) be subject \(i\)’s individual treatment effect: the difference between \(i\)’s posttest score if \(i\) were randomized to treatment and their score if randomized to control. Let \(\mathcal {T}\) and \(\mathcal {C}\) be the samples of students randomized to treatment and control, respectively. Let \(\alpha _{ci}\) be \(i\)’s propensity to game the system if randomized to the control condition. \(\alpha _{ci}\) is defined for \(i\in \mathcal {T}\), as students in the treatment conditions still had a potential to game the system had they been randomized to control, even if this potential was never realized. Therefore, \(\alpha _{ci}\) is estimated from gaming the system behavior for \(\mathcal {C}\) and \(\alpha _{ci}\) is imputed for each \(\mathcal {T}\). This propensity to game the system is condition-specific and represents an estimate of whether students would have gamed the system if randomized to the control condition (i.e., Immediate Condition).
The principal effect is the treatment effect for the subgroup of students with a particular value for \(\alpha _c\):
\begin {equation} \begin {split} \label {FPLSMode} \tau (\alpha ) = E[\tau | a_{t}=\alpha ] \end {split} \end {equation}
To estimate the function \(\tau (\alpha )\), we (1) estimate \(\alpha _c\) for \(\mathcal {C}\) as a function of pre-treatment covariates observed in both groups, (2) use that model to impute \(\alpha _C\) for each \(\mathcal {T}\), (3) estimate \(\tau (\alpha )\) by including a treatment interaction in a linear regression model. The models are estimated using iterations through these steps in a Bayesian principal stratification model with a continuous variable consisting of measurement and outcome submodels, as outlined by (Jin and Rubin, 2008) and (Page, 2012).
Measurement Submodel: First, we estimate \(\alpha _c\) by running a multilevel logistic submodel predicting whether the gaming detector identified the students in the treatment condition to have gamed the system on each twenty-second time clip as delineated in the equation 2. Let \(G_{cji}\) be a binary indicator of whether student \(i\) gamed the system during time-clip \(c\) when working on problem \(j\). Let \(P_{ki}\) be covariate predictor \(k\) of \(K\) student-level predictors, which are measured at baseline for both \(\mathcal {T}\) and \(\mathcal {C}\) (described in section 4.4.2). Let the random intercepts be \(\mu _j\) for problems, \(\mu _i\) for students, \(\mu _t\) for teachers, and \(\mu _s\) schools, each modeled as independent and with normal distributions with means of zero and standard deviations estimated from the data.
\begin {equation} \begin {split} \label {measurmentmodel} logit(G_{cji}) = \gamma _{0}\, + \, \sum _{k=1}^K \gamma _{k}\mbox {P}_{ki}\, + \, \mu _{j}\, + \, \mu _{i}\, +\, \mu _{t} +\, \mu _{s} \end {split} \end {equation}
Using the parameters from Equation 2, students’ propensity to game the system in the immediate condition is defined as: \begin {equation} \label {e:alpha_ti} \alpha _i=\sum _{k=1}^K \gamma _{k}\mbox {P}_{ki} +\mu _i +\, \mu _{t} +\, \mu _{s} \end {equation}
We impute \(\alpha _{i}\) for \(\mathcal {T}\) with random draws from a normal distribution with mean \(\sum _k\gamma _{k}\mbox {P}_{ki} + \mu _{t[i]} +\mu _{s[i]}\), where \(\mu _{t[i]}\) and \(\mu _{s[i]}\) are the random intercepts for student \(i\)’s teacher and school, respectively, and standard deviation equal to the estimated standard deviation of \(\mu _i\). Note that randomization occurred at the student level (i.e., teachers had students in the treatment and control conditions in their classes). Therefore, we include the random intercepts for schools and teachers from submodel 2 in valuation for \(\alpha _{ci}\) for students in the control. However, \(\mu _i\) is unknown for \(\mathcal {T}\), but we can assume its distribution is the same in the two conditions because of the randomization.
Prior to the simultaneous estimation of the FLPS sub-models, we estimated the measurement submodel separately using the stan_glmer function from the rstanarm package (Goodrich et al., 2020) with different combinations and transformations of the pretest predictors and demographic variables to find a suitable model for the analysis. To build the measurement model, we randomly split the data into training (80%) and testing (20%) data sets.
Outcomes Submodel: To estimate the treatment effect for students with differing propensities to game the system, we run a multilevel linear regression predicting student’s post-test algebraic knowledge (\(Y_i\)). The submodel includes interaction between \(\alpha _{ci}\)—estimated for \(\mathcal {C}\) and randomly imputed for \(\mathcal {T}\)—and each \(Z_i\) indicator of being in the treatment condition. In practice there is one \(Z_i\) indicator for each treatment condition. Let the random effects for teacher be \(\nu _{t}\) and for school be \(\nu _s\).
\begin {equation} \label {outcomesmodel} Y_i = \beta _{0} + \, \beta _1\mbox {Z}_i +\, \beta _2 \alpha _{ci} +\,\beta _3\alpha _{ci}\mbox {Z}_i + \, \sum _{k=1}^K \lambda _{k}\mbox {P}_{ki} + \, \nu _{t} +\, \nu _{s}\ + \epsilon _i \end {equation}
Using the parameters from the submodel 4, the treatment effect for students with a particular propensity to game the system is modeled as
\begin {equation} \label {effectsequation} \tau (\alpha )=\beta _1+\beta _3 \alpha \end {equation}
Once again, there is one \(\tau (\alpha )\) for each treatment condition, as \(\beta _1\) and \(\beta _3\) are estimated for each treatment condition. Submodels 2 and 4 together formed a FLPS model, which we fit using the Stan Markov Chain Monte Carlo software through STAN (Arezooji, 2020). We ran 10,000 iterations of FLPS models using Markov chain Monte Carlo chains calling Stan through rstan (Carpenter et al., 2017) in R; code is posted on GitHub6. We evaluated convergence using trace plots and checking whether the \(\hat {R}\), which measures convergence by comparing between and within chain estimates of each parameter, was below the recommended threshold of 1.05 (Vehtari et al., 2021). The maximum \(\hat {R}\) for the model parameters was 1.04.
4.4. Data & Variables
The data for this study exists at two different levels: student and time clip. The student-level variables include the student pretest data, demographics, roster, and learning outcomes. Alternatively, the data used in gaming the system detector and the detector’s output is aggregated in twenty-second clips of the students’ usage of the program. Only time-clip data from the Immediate Condition is used, as we are estimating students’ propensity to game the system in that condition.
Notably, the study was conducted during the COVID-19 pandemic and involved considerable attrition. An attrition analysis based on United States Institute of Educational Sciences standards found that attrition did not bias the effect estimates of the conditions (Decker-Woodrow et al., 2023). The sample for the current study consists of 1976 students: 402 in the Immediate Condition, 385 in the Delayed Condition, 372 in the DragonBox, and 817 in FH2T. The students were taught by 36 teachers in 10 schools.
4.4.1. Gaming the System Detector Inputs and Output
Gaming labels were generated by adopting the methodology described by Paquette et al. (2015) to produce action clips for the gaming detector as described in Section 4.3.1. These clips capture actions taken by students in ASSISTments. Each clip contains unique identifiers: the student, the problem being worked on at the clip’s start, the skill associated with that problem, and the problem type. If the clip spanned multiple problems, the problem the student ended on was also documented. Additionally, the clips detail the start and end times of actions, their total duration, and, for attempts, the action’s correctness and the student’s answer. Supplementary data within the clips include indicators for hint requests, the number of hints requested during the clip, the total hints available for the problem, the use of a ‘bottom-out’ hint, and the total attempts by the student. Gaming labels were generated based on instances where the student’s actions in the clip met one or more rules indicative of gaming system behavior.
4.4.2. Pretreatment Predictors
To estimate students’ propensity to game the system, we used data from assessments administered prior to their use of their assigned condition. Pretest scores were collected by the original studies’ researchers: prior algebraic knowledge, math anxiety, and perceptual processing skills. Pretest algebraic knowledge was a variant of the learning outcome described below. The math anxiety assessment was adapted from the Math Anxiety Scale for Young Children-Revised (Chiu and Henry, 1990), which assessed negative reactions towards math, numeric inconfidence, and math-related worrying (Cronbach’s \(\alpha \)=.87; see the items on OSF7). Five items were adapted from the Academic Efficacy Subscale of the Patterns of Adaptive Learning Scale to assess math self-efficacy (Midgley et al. (2000); Cronbach’s \(\alpha \) = .82; see items on OSF8). The perceptual processing assessment evaluates students’ ability to detect mathematically equivalent and nonequivalent expressions as quickly as possible (see item on OSF9). The district also provided metadata on the students, including their demographics and most recent standardized state test scores in math. Demographic data included race/ethnicity, individualized education plan status (IEP), and English as a second or foreign language (ESOL) status. Race/ethnicity was dummy-coded, with white students as the reference category because they were the majority population.
We standardized (z-score) all continuous scores to improve model fit and ease interpretation. Log forms of assessment test times were also included in the models. We include polynomials of the pretest scores when they improved model fit. Missing data were imputed using single-imputation with the Random Forest routine implemented by the missForest package in R (Stekhoven and Buehlmann, 2012, R Core Team, 2016). The number of missing data for each student was included as a predictor in each submodel.
4.4.3. Learning Outcome
The learning outcome for the study is students’ algebraic knowledge, which was assessed using ten multiple-choice items from a previously validated measure of algebra understanding (Star et al. (2015); Cronbach’s \(\alpha \) = .89; see the items on OSF10). Four of the items evaluated conceptual understanding of algebraic equation-solving (e.g., the meaning of an equal sign), three evaluated procedural skills of equation-solving (e.g., solving for a variable), and three evaluated flexibility of equation-solving strategies (e.g., evaluating different equation-solving strategies). Together, these ten items assessed students’ knowledge in algebraic equation-solving, the improvement of which was the goal of the interventions. The learning outcome was assessed before and after the interventions. Students’ scores were standardized (z-score) to ease model fit and interpretation.
5. Results
5.1. Gaming Detector Outputs
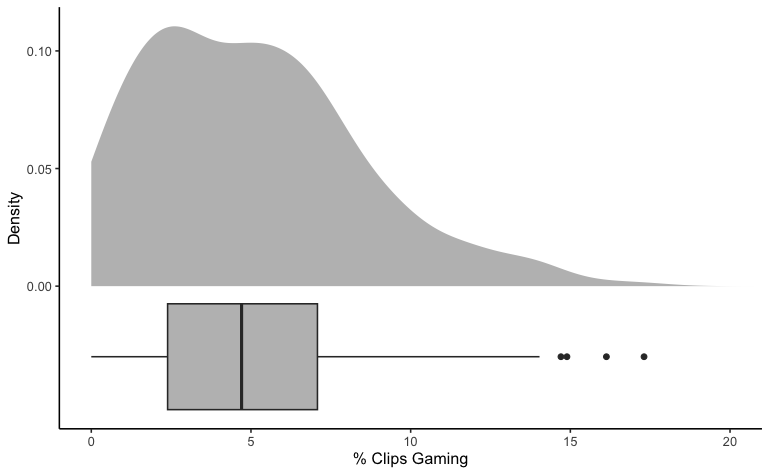
The students in the Immediate Condition produced 89,960 twenty-second clips of data. The gaming detector indicated that students gamed the system during 4.62% of the total clips. Most students (94.18%) were detected to have gamed the system at least once. Figure 2 displays a density and boxplot of the percentage of clips in which each student gamed the system during the study. Overall, students were detected to have gamed the system during approximately 5% of clips (mean = 5.10%, median = 4.71%, SD =3.64%,). However, this distribution has a positive skew. Almost a tenth (9.00%) of students were detected to have gamed during at least 10% of the clips. This suggests that while most students engage in some gaming, there is wide variation in student gaming behavior, and some students likely have a substantially higher propensity to game than others.
In almost three-quarters of the problems (74.35%), the detector did not detect any gaming. Notably, there was a small significant negative correlation between the gaming rate on each problem and the average accuracy on the problem (r = -0.21, p \(<\) 0.001). Furthermore, some problem types had significantly higher rates of gaming behaviors than others (F[5,244] = 6.403 p \(<\) 0.001). Students were more likely to game the system on ‘check all that apply’ problems compared with problems for which they had to submit a number (p \(<\) 0.001), variable (p = 0.016), algebraic expression (p = 0.020), or open response (p \(<\) 0.016). Furthermore, students were more likely to game the system on a multiple choice question than problems in which they had to submit a numeric answer (p = 0.015). Because the problems without gaming behavior would not be informative for assessing students gaming the system, we did not include these problems when estimating the measurement submodel.
5.2. Fully Latent Principal Stratification
Table 3 provides parameter estimates and relevant statistics for the measurement and outcome submodels.
| Measurement Submodel | Outcomes Submodel | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictors | Estimate | SD | P(\(>\)0) | P(\(<\)0) | Estimate | SD | P(\(>\)0) | P(\(<\)0) | |
| \(\alpha \) | -0.51 | 0.13 | 0.01 | 0.99 | |||||
| \(Z_{DelayedCondition}\) | -0.10 | 0.05 | 0.02 | 0.98 | |||||
| \(\alpha *Z_{DelayedCondition}\) | 0.10 | 0.07 | 0.90 | 0.10 | |||||
| \(Z_{FH2T}\) | 0.01 | 0.04 | 0.63 | 0.37 | |||||
| \(\alpha *Z_{FH2T}\) | -0.08 | 0.06 | 0.09 | 0.91 | |||||
| \(Z_{DragonBox}\) | 0.08 | 0.05 | 0.96 | 0.04 | |||||
| \(\alpha *Z_{DragonBox}\) | 0.04 | 0.07 | 0.71 | 0.29 | |||||
| Algebraic Procedural Knowledge | -0.06 | 0.04 | 0.09 | 0.91 | -0.01 | 0.03 | 0.44 | 0.56 | |
| Algebraic Conceptual Knowledge | -0.10 | 0.06 | 0.04 | 0.96 | 0.15 | 0.04 | 0.01 | 0.99 | |
| Algebraic Flexibility Knowledge | -0.05 | 0.04 | 0.14 | 0.86 | 0.01 | 0.03 | 0.58 | 0.42 | |
| Algebraic Knowledge Items Complete | -0.00 | 0.08 | 0.49 | 0.51 | 0.04 | 0.05 | 0.79 | 0.21 | |
| Algebraic Knowledge Time (Log) | -0.08 | 0.06 | 0.10 | 0.90 | -0.04 | 0.04 | 0.15 | 0.85 | |
| Math Anxiety | -0.18 | 0.12 | 0.06 | 0.94 | -0.04 | 0.08 | 0.28 | 0.72 | |
| Math Anxiety (Squared) | -0.05 | 0.03 | 0.05 | 0.95 | -0.01 | 0.02 | 0.24 | 0.76 | |
| Math Negative Reaction | 0.16 | 0.08 | 0.98 | 0.02 | 0.01 | 0.06 | 0.59 | 0.41 | |
| Math Numerical Confidence | 0.11 | 0.07 | 0.93 | 0.07 | 0.04 | 0.05 | 0.77 | 0.23 | |
| Math Self Efficacy | -0.04 | 0.04 | 0.21 | 0.79 | 0.03 | 0.03 | 0.81 | 0.20 | |
| Perceptual Sensitivity Score Part 1 | -0.06 | 0.04 | 0.08 | 0.92 | -0.00 | 0.03 | 0.48 | 0.52 | |
| Perceptual Sensitivity Time Part 1 (Log) | -0.10 | 0.06 | 0.04 | 0.96 | -0.01 | 0.04 | 0.42 | 0.58 | |
| Perceptual Sensitivity Score Part 2 | 0.03 | 0.04 | 0.71 | 0.29 | 0.08 | 0.03 | 0.01 | 0.99 | |
| Perceptual Sensitivity Time Part 2 (Log) | -0.05 | 0.05 | 0.16 | 0.84 | -0.03 | 0.03 | 0.13 | 0.87 | |
| Perceptual Sensitivity Score Part 3 | 0.01 | 0.05 | 0.60 | 0.40 | 0.00 | 0.04 | 0.52 | 0.48 | |
| Perceptual Sensitivity Time Part 4 (Log) | -0.06 | 0.06 | 0.13 | 0.87 | 0.04 | 0.04 | 0.86 | 0.14 | |
| State Test Score | -0.32 | 0.05 | 0.01 | 0.99 | 0.01 | 0.06 | 0.57 | 0.43 | |
| Female | -0.03 | 0.04 | 0.21 | 0.79 | 0.04 | 0.03 | 0.92 | 0.08 | |
| Hispanic | 0.09 | 0.13 | 0.75 | 0.25 | 0.16 | 0.09 | 0.98 | 0.02 | |
| Asian/Pacific Islander | -0.17 | 0.12 | 0.08 | 0.92 | 0.18 | 0.08 | 0.98 | 0.02 | |
| Black | 0.31 | 0.20 | 0.93 | 0.07 | 0.16 | 0.13 | 0.88 | 0.12 | |
| IEP | -0.02 | 0.04 | 0.26 | 0.74 | 0.02 | 0.02 | 0.76 | 0.24 | |
| EIP | 0.01 | 0.04 | 0.62 | 0.38 | 0.01 | 0.02 | 0.68 | 0.33 | |
| ESOL | -0.00 | 0.05 | 0.47 | 0.53 | -0.03 | 0.03 | 0.19 | 0.81 | |
| Gifted | -0.01 | 0.04 | 0.43 | 0.57 | 0.08 | 0.03 | 0.99 | 0.01 | |
| In-person Instruction | 0.04 | 0.13 | 0.60 | 0.40 | -0.10 | 0.07 | 0.06 | 0.94 | |
| Missing Data | 0.03 | 0.09 | 0.63 | 0.37 | 0.02 | 0.05 | 0.63 | 0.37 | |
5.2.1. Measurement Submodel
As described in section 4.3.2, before running the full FLPS model, we tested covariate combinations and transformations and validated the model using training and testing data sets. The model performed best when pretest sub-scores from the tests were included. Math anxiety had a non-linear relation to gaming behavior, so a polynomial transformation was included in the model. Our final model produced an adequate AUC of 0.87 on the testing data set.
The measurement submodel’s coefficients provide insight into which student characteristics predict gaming behavior in the Immediate Condition. Generally, lower-performing students tended to game the system more frequently. Students with lower scores on the math section of their state test were more likely to game the system (\(\gamma _{17}\) = -0.32, \(P(<0)\) = .99). This association was consistent with the albeit smaller associations between the algebraic knowledge sub-scores and the gaming behavior. Furthermore, there was a nonlinear association between math anxiety and gaming behavior. Students with higher math anxiety were also less likely to game the system (\(\gamma _{6}\) = -0.18, \(P(<0)\) = .94) than those with low math anxiety. This association was even greater for students with highest levels of math anxiety, as shown by the coefficient for math anxiety squared (\(\gamma _{7}\) = -0.05, \(P(<0)\) = .95). Students with a higher negative reaction toward math (\(\gamma _{8}\) = 0.16, \(P(>0)\) = .98) and with higher numeric confidence (\(\gamma _{9}\) = 0.11, \(P(>0)\) = .93) were more likely to game the system. Time spent on the algebraic knowledge test and the perceptual sensitivity learning sub-tests were all predictive of gaming behavior; students who took less time on these tests were more likely to game the system.
5.2.2. Outcomes Submodel
The outcomes submodel provides the parameter estimates that address whether students likely to game the system in the Immediate Condition would benefit from an alternative learning environment. As expected, students’ propensity to game the system (\(\alpha \)) was negatively associated with the outcome (\(\beta _{2}\) = -0.51, \(P(<0)\) = 0.99). However, the interactions between \(\alpha \) and the conditions varied widely.
First, the Delayed Condition had a negative main effect but a positive interaction. For students who had an average propensity to game the system in the Immediate Condition (\(\alpha = 0\)), the effect of the Delayed Condition was likely negative (\(\beta _{1-Delayed}\) = -0.10, \(P(<0)\) = 0.98). The interaction between students’ propensity to game the system and the Delayed Condition was likely positive (\(\beta _{3-Delayed}\) = 0.10, \(P(>0)\) = 0.90). Although the positive effect of the interaction balanced out the negative effect of the Delayed Condition, it did not mitigate the lower performance associated with students’ propensity to game the system. That is to say, the negative effect for the Delayed Condition was equivalent in magnitude to the positive effect of the other interaction; thus, a student with a high propensity to game the system (\(\alpha = 1\)) would have the same benefit from the Delayed Condition as a student with a low propensity to game the system (\(\alpha = 0\)) would from the Immediate Condition. However, the magnitude of the positive effect for students who game the system in the Delayed Condition does not outweigh the overall negative association of propensity to gaming the system on the student’s post-test scores. Therefore, the Delayed Condition likely does not mitigate the gaming behavior. These were consistent with our findings in (Vanacore et al., 2024), thus reproducing those results with a slightly different model.
Second, the results showed varied effects of gamification and the interactions between gamified programs and students’ propensity to game the system. The estimated effect of FH2T on students who have an average propensity to game the system in the Immediate Conidtion (\(\alpha = 0\)) was small, and we have low confidence that it is greater than zero (\(\beta _{1-FH2T}\) = 0.01, \(P(>0)\) = 0.63). Yet, the interaction between FH2T and propensity to game the system was likely negative (\(\beta _{3-FH2T}\) = -0.08, \(P(<0)\) = 0.91). Thus, contrary to our hypotheses, gamers would likely have been better off in the Immediate Feedback condition than in FH2T; however, these results were not consistent for DragonBox, which had a likely positive main effect (\(\beta _{1-DragonBox}\) = 0.08, \(P(>0)\) = 0.96), yet there is little evidence of an interaction with students’ propensity to game the system in the Immediate Condition (\(\beta _{3-DragonBox}\) = 0.04, \(P(>0)\) = 0.71).
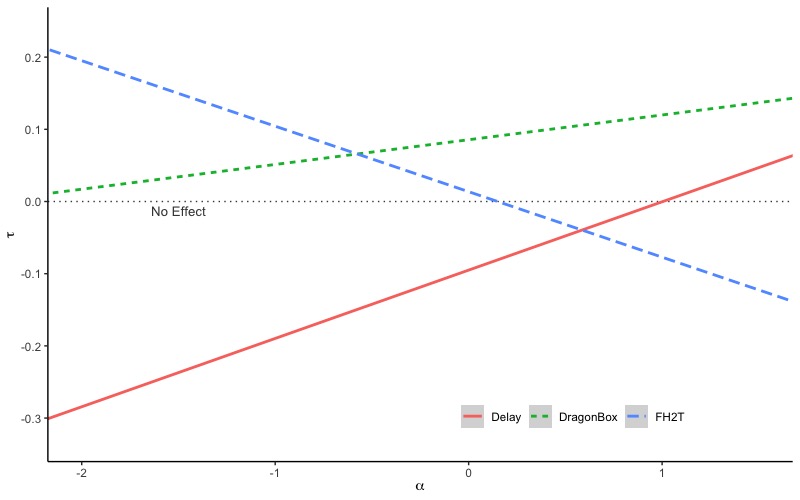
Figure 3 provides a visual representation of the interactions between \(\alpha \) and \(Z\) by plotting the effect sizes (\(\tau \)) for different levels of students’ propensity to game the system problem in the Immediate Condition (\(\alpha \)). Note that the mean of \(\alpha \) is zero and since all the covariates were standardized with means of zero, where the lines cross \(\alpha \) = 0 can be interpreted as the estimated effect for the average student with average gaming behavior (i.e., the main effect).
We have little evidence that the slope for the Dragon Box is different than zero. Therefore, it is most likely that students benefited from Dragon Box regardless of their propensity to game the system. However, we have higher confidence that the slopes for the Delayed Condition and FH2T are not zero. The Delayed Condition had an estimated negative impact on students with low or average gaming propensities, but those with very high propensities to game the system in the Immediate Condition may have experienced a positive effect. Note that only 5% of the student population had propensities to game the system this high (\(\alpha \) \(>\) 1), so this effect is only relevant for the most ardent gamers. For FH2T, we see the opposite trend: students with the lowest propensity to game the system experience the greatest effects, and those with an average or high propensity to game the system likely experience no effect or negative effects, respectively.
6. Discussion
The results suggest that students who tend to game the system respond differently to various CBLPs, but not in the way we hypothesized. Although the two gamified conditions produced different heterogeneity patterns for students who tend to game the system, neither of these conditions fully mitigated the negative association between gaming the system behaviors and learning. Similarly, delaying access to hints and feedback likely has a positive effect on students who tend to game the system, yet not enough to fully outweigh the potential negative effects of gaming behavior. Although we found evidence that some learning environments may provide marginal benefits to students who tend to game the system, overall, more targeted interventions may be necessary to reengage these students in the learning process so that they fully benefit from the CBLPs’ content.
6.1. Effects of Gamification on Students who Game the System
Although neither gamified condition had positive effect differentials on students with a high propensity to game the system, the interactions do provide some insight into how gamers tend to respond to different gamified environments. The effect was likely consistent for one of the gamified conditions (DragonBox), regardless of students’ propensity to game the system, whereas gamers in the other gamified condition (FH2T) experienced negative effects. This suggests that gamification alone is not the only factor influencing students’ behaviors and outcomes. Previous research on the relationship between gaming the system and gamification found that a gamified version of a CBLP did mitigate the gaming behavior and positively impacted student outcomes (Richey et al., 2021). In our study, the differences in heterogeneity patterns across platforms that shared many features of gamification (e.g., performance-based feedback, multiple paths to solutions, the ability to replay problems, and dynamic manipulation of equations) highlight that even slight variations in how a program is gamified may be more important than whether a program is gamified at all in terms of impacting students’ behavior and learning.
It is possible that FH2T did not benefit gamers because the goals are more abstract than traditional problems. Students needed to find the most efficient path to the solution by manipulating the expressions and equations on the screen as opposed to submitting answers to traditional problems. Furthermore, the evaluation system in the game is not delineated prior to playing and is meant to be intuited by the students as they play. As previous research suggests that abstractness and ambiguity may induce gaming behaviors (Baker et al., 2009), one possible explanation is that students who are likely to game the system in the Immediate Condition become even more frustrated by FH2T, causing them to disengage with the activity to a greater extent than they would have in a traditional CBLP environment. This may explain in part why FH2T had the greatest effects on students with the highest pretest scores (Decker-Woodrow et al., 2023), who were the students who were least likely to game the system.
However, DragonBox had a likely consistent positive effect regardless of students’ propensity to game the system, despite similar gamification features and a similar dynamic approach in teaching students the concept of equivalency to FH2T. Yet some key differences between these CBLPs may point to reasons for DragonBox’s effectiveness among gamers. First, DragonBox allows students to engage with algebraic equivalency without interacting with traditional math symbols. Second, the activity’s mathematical goal is embedded in a gamified narrative: freeing the dragon from the box. Finally, students learn the game’s goals through animated interactions before learning the algebraic principles. These elements may have alleviated tendencies towards unproductive learning behaviors enough so that students benefited regardless of propensity to game the system. More research is necessary to determine exactly why there were stark differences in the effect trajectories between the two gamified conditions.
6.2. Effect of Assistance on Students who Game the System
The positive interaction between students’ propensity to game the system and the Delayed Condition indicates that the impact of on-demand hints and feedback on student performance in a CBLP are heterogeneous. The differences in effects are likely attributed to how students use assistance features. Those who exploit hints excessively or rely on trial-and-error methods to complete assignments would potentially benefit from restricted or delayed access to immediate hints and feedback. Nevertheless, although on-demand hints and immediate feedback were not available in the Delayed Condition, the decrease in performance associated with gaming behavior was not completely mitigated. Therefore, these results suggest that while removing on-demand instruction may assist students inclined towards gaming the system, further intervention is likely required to fully alleviate the detrimental effects of such behavior and address the behavior’s root causes.
Delaying hints and feedback can be viewed as a proactive intervention targeting gaming the system behavior. This approach, similar to others employed in previous research (Aleven et al., 2006, Murray and VanLehn, 2005), uses a uniform approach for all students. The differential effect observed for delayed condition supports Murray and VanLehn (2005)’s suggestion that discouraging certain students from using hints may be beneficial for some students despite the overall negative impact on the student population; however, it is notable that only a small minority of the most ardent gamers may have benefited from delaying hints and feedback access.
A possible approach to address the varying effects includes withholding instant hints and feedback when students exhibit gaming behaviors, thus providing a focused corrective measure to steer their attention back to learning from the task at hand. Such a strategy would preserve the availability of real-time help for students who use the system appropriately while potentially benefiting those who exploit the system whenever they engage with it properly. An adaptable system like this could also lessen the damaging impact of manipulative behaviors by permitting gamers to reap the benefits of both instant and delayed hints and feedback. Nevertheless, this is unlikely to mitigate the antecedents of gaming fully without additional remediation. Furthermore, it is crucial to recognize that adopting this method could lead to feelings of frustration and a loss of engagement in some students, making it important to further explore and validate these ideas through additional causal research.
6.3. Combining Detection Models with FLPS
This study also illustrates the possible benefits of integrating detection and causal methods within EDM to explore how systems should effectively respond after identifying certain behaviors or latent states. Using artificial intelligence for detection purposes in CBLPs often leads learning experience designers to confront the dilemma of subsequent steps (for example, “Now that we know a student is frustrated, what do we do?”). FLPS offers a solution by pairing detector outputs with causal models to determine which program features may uniquely benefit students with particular behavioral patterns. Although rule-based detection methods were employed in our current investigation, future research could merge AI prediction systems with FLPS to go beyond assessing student experiences and behaviors in CBLPs to identify optimal alterations within these programs to boost their educational effectiveness.
7. Limitations & Future Directions
Although our findings suggest that the CBLPs’ impacts differ based on students’ tendencies to game the system, it is important to acknowledge the limitations of this analysis. There remains some uncertainty regarding whether the main and interaction effects in the model significantly differ from zero. Overall, for the estimates we considered likely to be different from zero, there was at most a 10% posterior probability that the true parameter had the opposite sign compared to the estimate presented in this paper. Thus, it is important that future research substantiate these findings to increase the certainty of their veracity.
Furthermore, while this study provides information about how students who game the system in a traditional CBLP respond to alternative CBLPs, it does not fully illuminate why. The patterns of effect sizes found here do not provide a simple principle for addressing gaming the system behaviors. More research is necessary to understand why some interventions work well for gamers whereas others do not.
The current study also does not address whether gaming behaviors are consistent across programs or whether the differential impact of these conditions is a function of changes in gaming behaviors. Future work should consider whether students’ gaming behaviors are consistent across programs. This could be done using causal mediation analysis to evaluate whether variation in gaming behavior mediates the relation between conditions and learning outcomes.
Another limitation of this study is that the FLPS results depend on the gaming detector’s accuracy. If there are systematic errors in the gaming detector, those errors should be considered while interpreting the FLPS model results. For example, some students may be gaming the system in principle but still have lower action rates. The Cognitive Model may not detect these students, and their propensities to game the system may be underestimated. The effect heterogeneity does not apply to profiles of gamers who are not detected. Conversely, if students are systematically misidentified as gaming, they will also be misidentified as part of gaming strata, which may influence the heterogeneity effects.
Finally, it is important to acknowledge the constraints inherent to the use of FLPS. The estimated impacts using FLPS heavily depend on the inherent quality of the model itself, and it remains uncertain how inaccuracies in estimating the model could potentially lead to biased outcomes. Future research should focus on gaining a more accurate understanding of how to assess these models to confirm that they furnish impartial appraisals of intervention effects.
8. Conclusion
The study indicates that students who are likely to game the system respond differently to various CBLPs, with none of the tested conditions fully mitigating the adverse effects of gaming the system. Delayed access to hints and feedback potentially benefits such students; however, the effect size was not large enough to outweigh the effect of their gaming tendencies on learning completely. This highlights the need for targeted interventions to help these students fully benefit from CBLPs’ content.
The studied gamified conditions produced inconsistent heterogeneity patterns—one (DragonBox) showed a consistent effect regardless of gaming tendencies, whereas the other (FH2T) indicated adverse effects for gamers despite the fact that these programs employed many similar gamification methods. This emphasizes that how a program is gamified, rather than the mere presence of gamification, might be key in influencing student behavior. It is possible that FH2T’s abstract goals caused more student frustration and consequent disengagement for students who were likely to game. On the other hand, DragonBox exhibited a positive effect independent of the student’s propensity to game the system, possibly attributable to its emphasis on taking abstract mathematical processes and teaching them through non-mathematical puzzles. However, understanding the differences in heterogeneity patterns across the gamified conditions warrants further research.
The promising interaction between students’ gaming tendencies and the Delayed Condition suggests that restricting immediate hints and feedback for those gaming the system might be effective at ameliorating some of the effects of gaming behaviors. Nevertheless, such a strategy could lead to feelings of frustration and decreased engagement in some students. Consequently, more research is necessary to validate these ideas and investigate further interventions.
Acknowledgments
The authors would like to thank past and current funders, including IES (R305D210036, R305N210049, R305D210031, R305A170137, R305A170243, R305A180401, R305A120125 & R305R220012 ), NSF (2118725, 2118904, 1950683, 1917808, 1931523, 1940236, 1917713, 1903304, 1822830, 1759229, 1724889, 1636782, & 1535428), GAANN (P200A120238, P200A180088, P200A150306 & P200A150306), EIR (U411B190024 S411B210024, & S411B220024), ONR (N00014-18-1-2768), NIH (via SBIR R44GM146483), Schmidt Futures, BMGF, CZI, Arnold, Hewlett and a $180,000 anonymous donation. The opinions expressed in this paper are those of the authors and do not represent the views of the funders.
References
- Abrahamson, D., Nathan, M. J., Williams-Pierce, C., Walkington, C., Ottmar, E. R., Soto, H., and Alibali, M. W. 2020. The future of embodied design for mathematics teaching and learning. Frontiers in Education 5, 1–29.
- Adams, D. M., McLaren, B. M., Durkin, K., Mayer, R. E., Rittle-Johnson, B., Isotani, S., and van Velsen, M. 2014. Using erroneous examples to improve mathematics learning with a web-based tutoring system. Computers in Human Behavior 36, 401–411.
- Adjei, S. A., Baker, R. S., and Bahel, V. 2021. Seven-year longitudinal implications of wheel spinning and productive persistence. In Artificial Intelligence in Education: 22nd International Conference (AIED 2021), I. Roll, D. McNamara, S. Sosnovsky, R. Luckin, and D. V., Eds. Springer International Publishing, 16–28.
- Aleven, V. and Koedinger, K. R. 2000. Limitations of student control: Do students know when they need help? In Intelligent Tutoring Systems, G. Gauthier, C. Frasson, and K. VanLehn, Eds. Lecture Notes in Computer Science. Springer, Berlin, Heidelberg, 292–303.
- Aleven, V., McLaren, B., Roll, I., and Koedinger, K. 2006. Toward meta-cognitive tutoring: A model of helpseeking with a cognitive tutor. International Journal of Artificial Intelligence in Education 16, 101–130.
- Aleven, V., Roll, I., McLaren, B. M., and Koedinger, K. R. 2016. Help helps, but only so much: Research on help seeking with intelligent tutoring systems. International Journal of Artificial Intelligence in Education 26, 1 (Mar), 205–223.
- Arezooji, D. M. 2020. A markov chain monte-carlo approach to dose-response optimization using probabilistic programming (rstan). arXiv Preprint.
- Baker, R., Carvalho, A., Raspat, J., Aleven, V., and Koedinger, K. R. 2009. Educational software features that encourage and discourage “gaming the system”. In Artificial Intelligence in Education: 14th International Conference (AIED 2009), S. D. Craig and D. Dicheva, Eds. Vol. 14. Springer International Publishing, 475–482.
- Baker, R., Walonoski, J., Heffernan, N., Roll, I., Corbett, A., and Koedinger, K. 2008. Why students engage in “gaming the system” behavior in interactive learning environments. Journal of Interactive Learning Research 19, 2, 185–224.
- Baker, R. S., Corbett, A. T., Koedinger, K. R., and Wagner, A. Z. 2004. Off-task behavior in the cognitive tutor classroom: when students ”game the system”. In Proceedings of the Conference on Human Factors in Computing Systems (CHI 2004). Association for Computing Machinery, 383–390.
- Baker, R. S. J. d., Corbett, A. T., Koedinger, K. R., Evenson, S., Roll, I., Wagner, A. Z., Naim, M., Raspat, J., Baker, D. J., and Beck, J. E. 2006. Adapting to when students game an intelligent tutoring system. In Intelligent Tutoring Systems: 8th International Conference, M. Ikeda, K. D. Ashley, and T.-W. Chan, Eds. Springer, Jhongil, Taiwan, 392–401.
- Baker, R. S. J. D., Corbett, A. T., Koedinger, K. R., and Roll, I. 2006. Generalizing detection of gaming the system across a tutoring curriculum. In 8th International Conference of Intelligent Tutoring Systems (ITS 2006), M. Ikeda, K. D. Ashley, and T.-W. Chan, Eds. Spinger, 402–411.
- Baker, R. S. J. d., Corbett, A. T., Roll, I., and Koedinger, K. R. 2008. Developing a generalizable detector of when students game the system. User Modeling and User-Adapted Interaction 18, 3 (Aug), 287–314.
- Baker, R. S. J. d., Mitrović, A., and Mathews, M. 2010. Detecting gaming the system in constraint-based tutors. In User Modeling, Adaptation, and Personalization, P. De Bra, A. Kobsa, and D. Chin, Eds. Lecture Notes in Computer Science. Springer, Berlin, Heidelberg, 267–278.
- Butler, A. C. and Woodward, N. R. 2018. Toward consilience in the use of task-level feedback to promote learning. Psychology of Learning and Motivation 69, 1–38.
- Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M. A., Guo, J., Li, P., and Riddell, A. 2017. Stan: A probabilistic programming language. Journal of statistical software 76, 1–32.
- Cayton-Hodges, G. A., Feng, G., and Pan, X. 2015. Tablet-based math assessment: What can we learn from math apps? Journal of Educational Technology & Society 18, 2, 3–20.
- Chiu, L.-H. and Henry, L. L. 1990. Development and validation of the mathematics anxiety scale for children. Measurement and evaluation in counseling and development 23, 3, 121–127.
- Corbett, A. T. and Anderson, J. R. 1994. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction 4, 4 (Dec), 253–278.
- Dang, S. and Koedinger, K. 2019. Exploring the link between motivations and gaming. In Proceedings of The 12th International Conference on Educational Data Mining (EDM 2019), C. F. Lynch, A. Merceron, M. Desmarais, and N. R., Eds. International Educational Data Mining Society, 276–281.
- Decker-Woodrow, L. E., Mason, C. A., Lee, J.-E., Chan, J. Y.-C., Sales, A., Liu, A., and Tu, S. 2023. The impacts of three educational technologies on algebraic understanding in the context of covid-19. AERA Open 9, 23328584231165919.
- Dieter, K. C., Studwell, J., and Vanacore, K. P. 2020. Differential responses to personalized learning recommendations revealed by event-related analysis. In Proceedings of the 13th International Conference on Educational Data Mining (EDM 2020), A. N. Rafferty, J. Whitehill, C. Romero, and V. Cavalli-Sforza, Eds. Vol. 13. International Educational Data Mining Society, Online, 736–742.
- Dihoff, R. E., Brosvic, G. M., and Epstein, M. L. 2003. The role of feedback during academic testing: The delay retention effect revisited. The Psychological Record 53, 4, 533–548.
- Dolonen, J. A. and Kluge, A. 2015. Algebra learning through digital gaming in school. In Exploring the Material Conditions of Learning: The Computer Supported Collaborative Learning (CSCL) Conference 2015. Vol. 1. International Society of the Learning Sciences, Inc. [ISLS]., 252–259.
- Feng, M. and Heffernan, N. T. 2006. Informing teachers live about student learning: Reporting in the assistments system. Technology Instruction Cognition and Learning 3, 1–14.
- Frangakis, C. E. and Rubin, D. B. 2002. Principal stratification in causal inference. Biometrics 58, 1, 21–29.
- Garris, R., Ahlers, R., and Driskell, J. E. 2002. Games, motivation, and learning: A research and practice model. Simulation& Gaming 33, 4 (Dec.), 441–467.
- Gaston, J. and Cooper, S. 2017. To three or not to three: Improving human computation game onboarding with a three-star system. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems (CHI 2017), G. Mark and P. Fussell, Eds. ACM, Denver Colorado USA, 5034–5039.
- Gee, J. P. 2005. Learning by design: Good video games as learning machines. E-Learning and Digital Media 2, 1.
- Goldstone, R. L., Landy, D. H., and Son, J. Y. 2010. The education of perception. Topics in Cognitive Science 2, 2, 265–284.
- Goodrich, B., Gabry, J., Ali, I., and Brilleman, S. 2020. rstanarm: Bayesian applied regression modeling via Stan. R Package Version 2.21.1.
- Gurung, A., Baral, S., Lee, M. P., Sales, A. C., Haim, A., Vanacore, K. P., McReynolds, A. A., Kreisberg, H., Heffernan, C., and Heffernan, N. T. 2023. How common are common wrong answers? crowdsourcing remediation at scale. In Proceedings of the Tenth ACM Conference on Learning@ Scale (L@S2023), D. Spikol, A. P. Viberg, A. Martínez-Monés, and P. Guo, Eds. Association for Computing Machinery, 70–80.
- Gurung, A., Baral, S., Vanacore, K. P., Mcreynolds, A. A., Kreisberg, H., Botelho, A. F., Shaw, S. T., and Hefferna, N. T. 2023. Identification, exploration, and remediation: Can teachers predict common wrong answers? In LAK23: 13th International Learning Analytics and Knowledge Conference. Association for Computing Machinery, 399–410.
- Heffernan, N. T. and Heffernan, C. L. 2014. The assistments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education 24, 4 (Oct), 470–497.
- Jin, H. and Rubin, D. B. 2008. Principal stratification for causal inference with extended partial compliance. Journal of the American Statistical Association 103, 481, 101–111.
- Juul, G. J. 2009. Routledge, Chapter Fear of Failing? The Many Meanings of Difficulty in Video, 237–252.
- Karagiorgas, D. N. and Niemann, S. 2017. Gamification and game-based learning. Journal of Educational Technology Systems 45, 4 (June), 499–519.
- Landers, R. N. 2014. Developing a theory of gamified learning: Linking serious games and gamification of learning. Simulation& Gaming 45, 6 (Dec.), 752–768.
- Lee, M., Croteau, E., Gurung, A., Botelho, A., and Heffernan, N. 2023. Knowledge tracing over time: A longitudinal analysis. In The Proceedings of the 16th International Conference on Educational Data Mining (EDM 2023)., M. Feng, T. Kaser, and P. Talukdar, Eds. International Educational Data Mining Society, 296–301.
- Levin, N., Baker, R., Nasiar, N., Stephen, F., and Hutt, S. 2022. Evaluating gaming detector model robustness over time. In Proceedings of the 15th International Conference on Educational Data Mining (EDM 2022), A. Mitrovic and N. Bosch, Eds. International Educational Data Mining Society, 398–405.
- Lu, X., Sales, A., and Heffernan, N. T. 2021. Immediate versus delayed feedback on learning: Do people’s instincts really conflict with reality? Journal of Higher Education Theory and Practice 21, 16 (Dec.).
- Lu, X., Wang, W., Motz, B. A., Ye, W., and Heffernan, N. T. 2023. Immediate text-based feedback timing on foreign language online assignments: How immediate should immediate feedback be? Computers and Education Open 5, 1–12.
- Malkiewich, L. J., Lee, A., Slater, S., Xing, C., and Chase, C. C. 2016. No lives left: How common game features could undermine persistence, challenge-seeking and learning to program. In Proceedings of The International Conference of the Learning Sciences (ICLS) 2016. International Society of the Learning Sciences, 186–193.
- McKernan, B., Martey, R. M., Stromer-Galley, J., Kenski, K., Clegg, B. A., Folkestad, J. E., Rhodes, M. G., Shaw, A., Saulnier, E. T., and Strzalkowski, T. 2015. We don’t need no stinkin’ badges: The impact of reward features and feeling rewarded in educational games. Computers in Human Behavior 45, 299–306.
- McLaren, B. M., Van Gog, T., Ganoe, C., Karabinos, M., and Yaron, D. 2016. The efficiency of worked examples compared to erroneous examples, tutored problem solving, and problem solving in computer-based learning environments. Computers in Human Behavior 55, 87–99.
- Midgley, C., Maehr, M. L., Hruda, L. Z., Anderman, E., Anderman, L., Freeman, K. E., Urdan, T., et al. 2000. Manual for the patterns of adaptive learning scales. University of Michigan.
- Mihaela, C. and Hershkovitz, A. 2009. The impact of off-task and gaming behaviors on learning: Immediate or aggregate? In Frontiers in Artificial Intelligence and Applications: Building Learning Systems that Care: From Knowledge Representation to Affective Modelling, V. Dimitrova, R. Mizoguchi, B. du Boulay, and A. Graesser, Eds. Vol. 200. Ios Press, 507–514.
- Murray, R. C. and VanLehn, K. 2005. Effects of dissuading unnecessary help requests while providing proactive help. In Artificial Intelligence in Education: 12th International Conference (AIED 2005), C.-K. Looi, G. McCalla, B. Bredeweg, and J. Breuker, Eds. Springer International Publishing, 887–889.
- Ottmar, E., Lee, J.-E., Vanacore, K., Pradhan, S., Decker-Woodrow, L., and Mason, C. A. 2023. Data from the efficacy study of from here to there! a dynamic technology for improving algebraic understanding. Journal of Open Psychology Data 11, 1 (Apr), 1–15.
- Page, L. C. 2012. Principal stratification as a framework for investigating mediational processes in experimental settings. Journal of Research on Educational Effectiveness 5, 3, 215–244.
- Page, L. C., Feller, A., Grindal, T., Miratrix, L., and Somers, M.-A. 2015. Principal stratification: A tool for understanding variation in program effects across endogenous subgroups. American Journal of Evaluation 36, 4 (Dec), 514–531.
- Paquette, L. and Baker, R. S. 2017. Variations of gaming behaviors across populations of students and across learning environments. In Artificial Intelligence in Education: 17th International Conference (AIED 2017), E. André, R. Baker, X. Hu, M. M. T. Rodrigo, and B. du Boulay, Eds. Springer International Publishing, Cham, 274–286.
- Paquette, L. and Baker, R. S. 2019. Comparing machine learning to knowledge engineering for student behavior modeling: a case study in gaming the system. Interactive Learning Environments 27, 5–6 (Aug), 585–597.
- Paquette, L., Baker, R. S., de Carvalho, A., and Ocumpaugh, J. 2015. Cross-system transfer of machine learned and knowledge engineered models of gaming the system. In User Modeling, Adaptation and Personalization, F. Ricci, K. Bontcheva, O. Conlan, and S. Lawless, Eds. Lecture Notes in Computer Science. Springer International Publishing, Cham, 183–194.
- Paquette, L., de Carvalho, and A. M. J. A., & Baker, R. S. 2014. Towards understanding expert coding of student disengagement in online learning. In Proceedings of the 36th Annual Cognitive Science Conference, P. Bello, M. Guarini, M. McShane, and B. Scassellati, Eds. CogSci, 1–6.
- Pardos, Z. A., Baker, R. S. J. D., San Pedro, M. O. C. Z., Gowda, S. M., and Gowda, S. M. 2014. Affective states and state tests: Investigating how affect and engagement during the school year predict end-of-year learning outcomes. Journal of Learning Analytics 1, 1, 107–128.
- Patikorn, T. and Heffernan, N. T. 2020. Effectiveness of crowd-sourcing on-demand assistance from teachers in online learning platforms. In L@S 2020 - Proceedings of the 7th ACM Conference on Learning @ Scale. Association for Computing Machinery, 115–124.
- Phye, G. D. and Andre, T. 1989. Delayed retention effect: Attention, perseveration, or both? Contemporary Educational Psychology 14, 2 (Apr), 173–185.
- Prihar, E., Patikorn, T., Botelho, A., Sales, A., and Heffernan, N. 2021. Toward personalizing students’ education with crowdsourced tutoring. In L@S 2021 - Proceedings of the 8th ACM Conference on Learning @ Scale. Association for Computing Machinery, 37–45.
- R Core Team. 2016. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
- Razzaq, L., Heffernan, N. T., and Lindeman, R. W. 2007. What level of tutor interaction is best? Frontiers in Artificial Intelligence and Applications 158, 222–229.
- Richey, J. E., Zhang, J., Das, R., Andres-Bray, J. M., Scruggs, R., Mogessie, M., Baker, R. S., and McLaren, B. M. 2021. Gaming and confrustion explain learning advantages for a math digital learning game. In Artificial Intelligence in Education: 22nd International Conference, I. Roll, D. McNamara, S. Sosnovsky, R. Luckin, and V. Dimitrova, Eds. Lecture Notes in Computer Science. Springer International Publishing, Utrecht, The Netherlands, 342–355.
- Rodrigo, M. M. T., Baker, R. S. J. d., D’Mello, S., Gonzalez, M. C. T., Lagud, M. C. V., Lim, S. A. L., Macapanpan, A. F., Pascua, S. A. M. S., Santillano, J. Q., Sugay, J. O., Tep, S., and Viehland, N. J. B. 2008. Comparing learners’ affect while using an intelligent tutoring system and a simulation problem solving game. In Intelligent Tutoring Systems, B. P. Woolf, E. Aïmeur, R. Nkambou, and S. Lajoie, Eds. Lecture Notes in Computer Science. Springer, Berlin, Heidelberg, 40–49.
- Roschelle, J., Feng, M., Murphy, R. F., and Mason, C. A. 2016. Online mathematics homework increases student achievement. AERA Open 2, 4 (Oct.), 2332858416673968.
- Sales, A. C. and Pane, J. F. 2019. The role of mastery learning in an intelligent tutoring system: Principal stratification on a latent variable. The Annals of Applied Statistics 13, 1 (Mar), 420–443.
- Shute, V. J. 2008. Focus on formative feedback. Review of Educational Research 78, 1 (Mar), 153–189.
- Siew, N. M., Geofrey, J., and Lee, B. N. 2016. Students’ algebraic thinking and attitudes towards algebra: The effects of game-based learning using dragonbox 12 + app. The Research Journal of Mathematics and Technology 5, 1, 66–79.
- Star, J. R., Pollack, C., Durkin, K., Rittle-Johnson, B., Lynch, K., Newton, K., and Gogolen, C. 2015. Learning from comparison in algebra. Contemporary Educational Psychology 40, 41–54.
- Stekhoven, D. J. and Buehlmann, P. 2012. Missforest - non-parametric missing value imputation for mixed-type data. Bioinformatics 28, 1, 112–118.
- Torres, R., Toups, Z. O., Wiburg, K., Chamberlin, B., Gomez, C., and Ozer, M. A. 2016. Initial design implications for early algebra games. In Proceedings of the 2016 Annual Symposium on Computer-Human Interaction in Play Companion Extended Abstracts. CHI PLAY Companion ’16. Association for Computing Machinery, New York, NY, USA, 325–333.
- Vanacore, K., Gurung, A., Sales, A., and Heffernan, N. T. 2024. The effect of assistance on gamers: Assessing the impact of on-demand hints & feedback availability on learning for students who game the system. In Proceedings of the 14th Learning Analytics and Knowledge Conference. Association for Computing Machinery, 462–472.
- Vanacore, K., Ottmar, E., Liu, A., and Sales, A. 2024. Remote monitoring of implementation fidelity using log-file data from multiple online learning platforms. Journal of Research on Technology in Education, 1–21.
- Vanacore, K., Sales, A., Liu, A., and Ottmar, E. 2023a. Benefit of gamification for persistent learners: Propensity to replay problems moderates algebra-game effectiveness. In Tenth ACM Conference on Learning @ Scale (L@S ’23), D. Spikol, O. Viberg, A. Martínez-Mones, and P. Guo, Eds. ACM, Copenhagen, Denmark, 164–173.
- Vanacore, K., Sales, A., Liu, A., and Ottmar, E. 2023b. Heterogeneous effects of game-based failure on student persistence in an online algebra game. In Society for Research Educational Effectiveness Conference (SREE 2023). SREE, 1–4.
- Vanacore, K., Sales, A. C., Hansen, B., Liu, A., and Ottmar, E. 2024. Effect of game-based failure on productive persistence: an application of regression discontinuity design for evaluating the impact of program features on learning-related behaviors. Available at Social Science Research Network 4789291.
- Vehtari, A., Gelman, A., Simpson, D., Carpenter, B., and Bürkner, P.-C. 2021. Rank-normalization, folding, and localization: An improved r hat for assessing convergence of mcmc (with discussion). Bayesian analysis 16, 2, 667–718.
- Walonoski, J. A. and Heffernan, N. T. 2006. Prevention of off-task gaming behavior in intelligent tutoring systems. In Intelligent Tutoring Systems: 8th International Conference, ITS 2006, Jhongli, Taiwan, June 26-30, 2006. Proceedings 8, T.-W. C. Mitsuru Ikeda, Kevin D. Ashley, Ed. Lecture Notes in Computer Science. Springer, 722–724.
- Williams, J. J., Kim, J., Rafferty, A., Maldonado, S., Gajos, K. Z., Lasecki, W. S., and Heffernan, N. 2016. Axis: Generating explanations at scale with learnersourcing and machine learning. In Proceedings of the Third (2016) ACM Conference on Learning @ Scale. L@S ’16. Association for Computing Machinery, New York, NY, USA, 379–388.
- Xia, M., Asano, Y., Williams, J. J., Qu, H., and Ma, X. 2020. Using information visualization to promote students’ reflection on “gaming the system” in online learning. In Proceedings of the Seventh ACM Conference on Learning @ Scale. L@S ’20. Association for Computing Machinery, New York, NY, USA, 37–49.
1Throughout this paper, we use the term ’gamers’ to mean students who tend to game the system and ‘gaming behaviors’ as behaviors indicative of gaming the system.
2The finding that delayed hints and feedback are beneficial for students who tend to game the system was first reported in Vanacore et al. (2024). The current paper extends these analyses to include two other conditions.
3The data can be accessed on the Open Science Foundation (OSF) repository after filling out a data exchange
agreement: https://osf.io/r3nf2/
5https://dragonbox.com/products/algebra-12
6https://github.com/kirkvanacore/FLPS_GamingTheSystem/tree/main/code/JEDM_code