Abstract

Experimental research on perception and cognition has shown that inherent and manipulated visual features of mathematics problems impact individuals’ problem-solving behavior and performance. In a recent study, we manipulated the spacing between symbols in arithmetic expressions to examine its effect on 174 undergraduate students’ arithmetic performance but found results that were contradictory to most of the literature (Closser et al., 2023). Here, we applied educational data mining (EDM) methods to that dataset at the problem level to investigate whether inherent features of the 32 experimental problems (i.e., problem composition, problem order) may have caused unintended effects on students’ performance. We found that students were consistently faster to correctly simplify expressions with the higher-order operator on the left, rather than right, side of the expression. Furthermore, average response times varied based on the symbol spacing of the current and preceding problems, suggesting that problem sequencing matters. However, including or excluding problem identifiers in analyses changed the interpretation of results, suggesting that the effect of sequencing may be impacted by other, undefined problem-level factors. These results advance cognitive theories on perceptual learning and provide implications for educational researchers: online experiments designed to investigate students’ performance on mathematics problems should include a variety of problems, systematically examine the effects of problem order, and consider applying different analytical approaches to detect effects of inherent problem features. Moreover, EDM methods can be a tool to identify nuanced effects on behavior and performance as observed through data from online platforms.

Keywords

Introduction

Experimental work in cognitive science has informed theories, tool designs, and practice in education (e.g., Booth et al., 2017; Butler et al., 2014; Higgins et al., 2019). Notably, experimental research on perception and cognition related to Gestalt principles of grouping over the past decade has shown that changes to the visual presentation of mathematics problems impacts individuals’ behavior and performance on problem solving. The effects of Gestalt principles of grouping have been tested using color as a highlighter (e.g., 3 + 4 + 5 = 3 + __ where the equals sign is highlighted in red font; Alibali et al., 2018), superfluous brackets (e.g., 7 + (6 * 3) – 2; Ngo et al., 2023), and spacing between symbols (e.g. 6*3  +  7 – 2 vs. 6  *  3+7–2; Landy and Goldstone, 2007, 2010; Harrison et al., 2020). Collectively, this body of research has contributed to theories of perceptual learning (e.g., Gibson, 1969; Gibson, 1970; Goldstone et al., 2017; see Szokolszky et al., 2019 for a review) and the creation of tools and technologies that leverage perceptual cues to support mathematics learning (e.g., Graspable Math: Ottmar et al., 2015; Mathematics Imagery Trainer: Abrahamson and Trninic, 2015). In turn, these research-based technological tools provide fine-grain process data for researchers to examine student cognition and learning in online contexts through methods of educational data mining (EDM).

The effects of spacing within mathematics notation on students’ performance has largely been replicated across institutions, age groups, and contexts. In general, students’ performance improves when viewing arithmetic problems with spacing that is congruent to the order of operations (e.g., 7*7 – 4) and decreases when viewing problems with incongruent spacing (e.g., 7  *  7+4). For example, Landy and Goldstone (2007, 2010) found that participants were most accurate and quickest when viewing congruent spacing and least accurate when viewing incongruent spacing. This finding has been observed in school-aged children (e.g., Braithwaite et al., 2016; Harrison et al., 2020) as well as college students (Landy and Goldstone, 2007, 2010; Rivera and Garrigan, 2016). Like the original studies by Landy and Goldstone (2007, 2010), we conducted a computer-based, within-subjects experiment with undergraduates to test the effects of spacing within mathematical expressions on problem-solving performance. However, our conceptual replication and extension of these studies in an online experiment revealed no effect of spacing on college students’ overall accuracy and median response time simplifying order-of-operations problems (Closser et al., 2023). Those findings prompted the current study to examine why the discrepancy between these experiments might have occurred from a methodological perspective and how differences in experimental design and data analysis affect interpretation.

Consequently, this project highlights a methodological gap that is critical to fill in order to draw accurate conclusions and use perceptual learning to inform designs of educational tools, assessments, and practice. We posit that EDM can help fill this methodological gap with data analytic techniques that identify subtle, unintended effects within the context of online education experiments or datasets. By analyzing how instructional materials and study design decisions impact student performance, we will be able to identify potential factors that influence study outcomes, inform future research that considers these factors in their design and data analysis, and build upon theories of perceptual learning to advance research, leading to translational science and implications for classroom practice.

Here, we use EDM methods to analyze the data from Closser et al. (2023) at the problem level to identify unintended effects on student performance at a granular level. Specifically, we examine whether and how the problem features (i.e., higher-order operator position) and study design choices (i.e., interleaving problem types) impacted students’ response times. These findings contribute to perceptual learning theory and provide guidelines for interdisciplinary research in online educational contexts.

Perceptual Learning in Mathematics

Theories of perceptual learning posit that the ways in which individuals process sensory information (i.e., visual, auditory, olfactory, tactile) changes as they accrue experience and develop expertise in a given area (Gibson, 1969). For example, compared to novices, chess masters can quickly memorize and recreate valid board set ups because they are able to leverage structural patterns in the board to interpret the arrangement as a given time point in a game (Chase and Simon, 1973). How do experts develop this keen ability to recognize patterns in sensory information? Demonstrated in Gestalt principles of grouping, we tend to visually perceive whole objects or groups rather than individual items when possible, especially when items are close in spatial proximity or share a similar color or size (Wagemans et al., 2012; Wertheimer, 1938). 

Much of the research in mathematics learning has shown the connection between perception and reasoning using a variety of visual cues based on the Gestalt principles of grouping (e.g., spacing, color, symbol choice and arrangement; see Closser et al., 2022, for a summary). These cues primarily alter the appearance, but not the meaning, of mathematics notation to tease apart whether and how the presentation of instructional materials impacts student outcomes. For example, using color to highlight salient mathematics structures has been shown to improve equation-solving strategies (e.g., equal sign in equations; Alibali et al., 2018). Adherence to such Gestalt principles of grouping has been seen across multiple topics in mathematics such as arithmetic (e.g., Harrison et al., 2020), algebra (e.g., Lee et al., 2022b), and geometry (e.g., Chan et al., 2019). Together, the variety of perceptual cues and their effects on students across mathematics subjects demonstrate the potential breadth of implications for using perceptual cues for teaching and learning mathematics.

In addition to the effects of perceptual features that only alter the problem appearance (e.g., color, spacing, superfluous brackets), students are also impacted by perceptual features of mathematics notation that are inherent to the problems themselves. For example, Chinese students differed in problem-solving speed depending on whether addition problems were presented with Arabic or Chinese numbers (Xinlin and Qi, 2003). Similarly, U.S. students used different strategies to solve algebraic problems that shared the same structure but presented in either variables (x + y – x) or numerals (4 + 6 – 4; Chan et al., 2022b). Liu and Braithwaite (2023) found that undergraduate students were more accurate on addition problems presented in decimals rather than fractions, but more accurate on multiplication problems when presented in fractions rather than decimals. Furthermore, undergraduate students (who demonstrated at least 80% accuracy on arithmetic problems) fixated sooner and longer on multiplication operators, as opposed to addition operators, in notation, suggesting that they might use multiplication operators as a signpost for where to start problem solving (Landy et al., 2008). Acknowledging that the perceptual features of mathematics content might affect student behavior and performance on tasks is necessary for interdisciplinary research on mathematics learning. Furthermore, as mastery in algebra may depend on the ability to quickly detect hierarchical structures of equations (e.g., higher order operators in order-of-operations problems; Marghetis et al., 2016), it is crucial to examine the factors that influence students’ ability to detect structures within problems.

Effects of Multiplication Operator Position

Problem composition, such as the position of higher-order operators in arithmetic and algebraic expressions, impacts students’ performance. Specifically, when the mathematical content remains the same, students in the U.S. simplify expressions more accurately and efficiently when they can apply a left-to-right solving strategy (e.g., 7 * 7 + 4) than when they cannot (e.g., 7 + 7 * 4; Bye et al., 2022; Ngo et al., 2023). For example, middle school students playing an online mathematics game were six times more likely to make an error on their first action when the problem structure did not allow for a left-to-right solving strategy (Bye et al., 2022). These findings support previous research showing middle school students’ tendency to solve problems from left to right, even at the risk of violating procedural rules like the order of operations (e.g., Kieran, 1979; Linchevski and Livneh, 1999; Norton and Cooper, 2001). Furthermore, they demonstrate students’ ingrained tendency to habitually read and solve problems from left to right without recognizing the hierarchical structures within problems (Chan et al., 2022b; Givvin et al., 2019), evidencing how students’ impulse to calculate follows the arrangement of the operators.

Taken together, this work shows that students’ performance on arithmetic problems may be, at least partially, explained by the presentation of problems rather than solely dependent on problem difficulty and/or student knowledge. Furthermore, the presentation of problems extends beyond perceptual cues (e.g., spacing) to include the left-to-right arrangement of symbols (e.g., higher-order operator position). Even though prior studies have counterbalanced the operator position when testing the effects of symbol spacing (e.g., Landy and Goldstone, 2007), to our knowledge, no studies have directly examined the effects of spacing and operator position simultaneously to test their relative independent influences on problem-solving performance. Using data from Closser et al. (2023), which revealed findings inconsistent with the literature, we aim to test the effects of symbol spacing and operator position simultaneously as an attempt to unpack this inconsistency. Specifically, going beyond prior research using average performance across problems in an activity, we use the problem-level data to delineate the effects of two perceptual cues—symbol spacing and operator position—on students’ problem-solving performance.

Effects of Problem Sequence and Negative Priming

In addition to perceptual features within problems, the sequential order of problems influences students’ mathematics performance and learning. It is well-established that interleaving, rather than blocking, information over time improves learning and memory (Ebbinghaus, 1913; Proctor, 1980). More specifically, findings from computational modeling suggest that blocking and interleaving each have a time and place in educational practice: blocked practice may be more effective for learning a skill whereas interleaving may be more effective for learning when to apply the skill (Li et al., 2013). However, the order in which problems are presented to students within educational research settings will likely depend on the study design (or design of the digital learning platform) and can contribute insights to the benefits of blocked vs. interleaving practice. For example, blocking arithmetic problems by equivalent sums (e.g., 2 + 3 = 5, 1 + 4 = 5) rather than the addend (e.g., 2 + 3 = 5, 2 + 4 = 6) seems to support second and third graders’ understanding of mathematical equivalence (McNeil et al., 2012), as blocking draws attention to the similarities between problems (i.e., equal sum vs. same addend) whereas interleaving draws students’ attention to the differences between problems (Carvalho and Goldstone, 2014).

Many of the experimental studies examining the effects of spacing as a perceptual cue on students’ order-of-operations performance used a between-subjects design to compare the effects of congruent (6*3  +  7) vs. incongruent spacing (6  *  3+7; Braithwaite et al., 2016; Harrison et al., 2020; Jiang et al., 2014). This study design choice (i.e., blocking problems by participants) allows researchers to systematically test the effects of spacing cues, but prevents them from exploring any potential effects of problem sequencing on students’ problem-solving performance. The sequence of problems may impact students’ performance due to other problem-level features. For example, in (Harrison et al. 2020), we used a between-subjects design to test the effects of congruent, incongruent, neutral, and mixed spacing on 5th-12th grade students’ problem-solving performance. We found that students who solved problems with congruent or neutral spacing were significantly more accurate than students who solved incongruent problems. Interestingly enough, students in the mixed condition, who solved problems that varied between congruent, neutral, and incongruent spacing, displayed significantly lower accuracy than students in the congruent condition but descriptively higher accuracy than those in the incongruent condition. We interpret this to mean that measuring students’ average performance might not have accurately accounted for problem-level variance and might have washed out the effects of viewing different spacing conditions on students’ problem-level performance. 

In particular, the spacing effect may be impacted by how problems are sequentially presented to students and the influence of negative priming between problems. If an individual views a stimulus that is to be ignored in a task, followed by a stimulus that is not to be ignored, their accuracy and response time may suffer on the latter task (Neill, 1977; see (Frings et al., 2015) for a review). For example, when individuals are told to identify the center letter on screen, if they view “DSD” followed by “FDF”, they may be slower to respond to the second stimulus (Neill, 1997). This phenomenon is known as the negative priming effect. In order-of-operations problems, the perceptual cues in each problem may prime students’ attention and performance on the following problem. In particular, when students transition from solving problems with perceptual cues to ignore (i.e., incongruent spacing) to problems with perceptual cues to leverage (i.e., congruent spacing), their problem-solving performance may decrease. Students may be primed by the first problem to ignore the spacing on the second problem, then realize that the congruent spacing on the second problem indeed supports problem solving. This process of inhibiting the spacing cues then suppressing the initial inhibition may potentially slow down students’ response time on the second problem.   

We posit that the negative priming effect may explain our previous finding (Closser et al., 2023) that, when order-of-operations problems with congruent vs. incongruent spacing were presented in a randomized order, college students were, on average, slower to correctly answer problems with congruent than incongruent spacing. In the previously reported analyses, we focused on conceptually replicating the spacing effects and exploring the role of inhibitory skills on students’ overall task performance; however, we did not explore the potential effects of multiplication operator position or problem sequence on students’ performance at the problem level. We consider the possibility that negative priming may contribute to the unexpected finding of longer response times on congruent vs. incongruent problems (Closser et al., 2023). Notably, effects of problem sequence have not been investigated in similar work on the spacing effect (e.g., Landy and Goldstone, 2007, 2010) and might identify conditions of the spacing effect. Leveraging EDM methodologies to uncover potential explanations for discrepancies in findings among the prior studies will yield guidelines for research that is necessary to inform instructional practice regarding how perceptual learning can facilitate problem-solving performance and learning.

Decoding Patterns in Mathematics Problem-solving using Educational Data Mining

In exploring the application of EDM methods to the analysis of student performance in mathematics, we align with a growing body of research that underscores the potential of EDM in educational settings. Prior research has demonstrated how data-driven methods can help in deciphering patterns in student performance (e.g. Kumar, 2021) and aligning those patterns with cognitive and behavioral constructs (e.g. Botelho et al., 2019, 2022; Lee et al., 2022a).

Research in digital learning platforms has resulted in numerous studies focused on the use of data to understand the processes of learning in addition to how they map onto learning outcomes. Baker et al. (2012), for example, explored how students’ interactions with arithmetic problems correlated with students’ depth of learning about math concepts. Koedinger et al. (2010) have similarly leveraged data-driven methodologies to understand students’ learning behaviors. More recent work by Gurung et al. (2021) specifically examined how students’ response time can provide insights into students’ cognitive engagement and consideration before approaching problem-solving tasks. Beyond this, additional studies in digital learning platforms have further explored the relation between problem presentation and student performance (Ostrow and Heffernan, 2014) as well as the importance of problem sequencing on student performance in mathematics (Beck and Mostow, 2008).

Studies employing the use of data mining methodologies have additionally focused on aspects of students’ perceptual fluency. For example, Rau, Mason, and Nowak (2016) utilized a machine learning approach to predict student performance on visual representation tasks. Related work from Sen et al. (2018) examined sequence effects on students’ perceptual fluency using machine learning- and human expert-generated visual sequences in the context of chemistry. Few works, however, have investigated similar aspects of perceptual learning through the lens of data-driven methods. These related projects demonstrate the value and growing practice of leveraging EDM to derive insights into student learning, prompting the application of EDM to gain insights as to how study design choices influence student cognition when problem solving in online contexts.

Current Study

Here, we examine whether the multiplication operator position affects students’ performance and whether there are any problem sequencing effects with symbol spacing during an online experiment. Together, these findings will help us tease apart when the effects of perceptual cues on students’ reasoning occur and provide methodological insights on how to design educational tools that effectively leverage these cues to impact learning. Going beyond prior work on student-level analyses, we use a multilevel approach to analyze the problem-level data from Closser et al. (2023) to answer the following questions:

1. How does the position of the multiplication operator, in addition to symbol spacing, impact students’ problem-solving response time on order-of-operations problems? Given that students tend to demonstrate a left-to-right solving strategy, we hypothesize that students will demonstrate quicker response times on problems where the higher-order operator (i.e., multiplication) is on the left-hand side. These problems are conducive to a left-to-right solving strategy (e.g., 3 * 7 + 7) whereas problems with the multiplication on the right-hand side cannot be solved with a left-to-right solving strategy (e.g., 8 + 4 * 4). Given the literature on Gestalt principles of grouping, we statistically control for spacing condition in order to more accurately estimate the operator position effects.

2. How does the sequence of congruent vs. incongruent symbol spacing impact students’ problem-solving response time on order-of-operations problems? We hypothesize that students may demonstrate the quickest response times when they transition between problems with the same type of symbol spacing (i.e., from congruent spacing to congruent spacing or from incongruent spacing to incongruent spacing). Accordingly, we predict that students’ response times may be slower when they transition from congruent to incongruent problems, and the slowest when they transition from incongruent to congruent problems. We reason that if students were attending to perceptual cues throughout the experimental problems, and realized that some problems contained incongruent spacing, they may have engaged in a one- or two-step process to inhibit their impulse to calculate by following the spacing cues before correctly simplifying the expression. For example, if students were attending to the spacing cues in an incongruent problem, they would just need to suppress their initial instinct of performing operations following the incongruent spacing. If they subsequently viewed a congruent problem, they may have been primed to suppress their initial impulse to follow the spacing cue then realized that their initial impulse was correct, potentially taking longer to solve the problem.

Methods

Plans for the online experiment were approved by our University’s Institutional Review Board. The experiment details and primary findings are reported in a separate OSF pre-registration and manuscript (Closser et al., 2023). The current analysis plan and our rationale are pre-registered on the Open Science Framework (https://osf.io/pcsyj). The cleaned data, code, and output are also shared on the project page (https://osf.io/uc5m9). 

Participants

We recruited undergraduate students enrolled in one or more psychology courses at a private university in the northeastern U.S. through the university’s online participant pool for psychology experiments. Students were compensated for their time with partial course credit. A total of 233 students started the experiment and 195 completed the entire study. Of the 195 students, 174 were included in the current research analysis, consistent with the prior report (Closser et al., 2023); the remaining students were excluded due to outlier performance (n = 16) or data logging errors (n = 5). Outlier performance was determined as three or more standard deviations above or below the mean on any experimental task (i.e., Stroop task and/or the experimental problems).

Of the 174 students, 173 students reported their age (M = 19.48 years, SD = 1.50, Min = 17, Max = 27) and 172 students reported their year in school. A total of 57 (33%) students reported being in their first year at the university, 43 (25%) in their second year, 34 (20%) in their third year, 32 (19%) in their fourth year, and two (1%) students in their fifth year. One student reported being in high school and three students reported “other”. Additionally, 171 students shared their gender: the sample included 95 (56%) females, 68 (40%) males, seven (4%) non-binary participants, and one agender participant.

Experimental Design and Procedure

The experiment was programmed using Psychopy and administered through Pavlovia, an online platform for behavioral data collection. After logging into SONA (a study and participant management system), students clicked a URL link to complete the study in a web browser on their personal devices. In the 30-minute experiment, students first completed a version of the Stroop task designed to assess inhibitory control. Following that task, students completed a total of 48 order-of-operations problems, presented individually with a text box below the problem for students to enter their answer. Students were instructed to find the answer and type their response into the text box as quickly and accurately as possible, then click “Next” to advance to the next problem without receiving correctness feedback. The first 16 order-of-operations problems were presented with neutral spacing (e.g., 4 * 3 − 10), serving as a baseline measure of students’ arithmetic performance. Next, students completed 32 experimental problems that were presented with congruent spacing (16 problems; e.g., 4*3   −  10) or incongruent spacing (16 problems; e.g., 4  *  3−10) in a predetermined, randomized order. At the end of the session, students were asked to report their age and gender. Aligned with our current research questions, we only examined students’ performance on the 32 experimental problems, as described below (see detailed description of the full study in Closser et al., 2023). 

We carefully designed the 32 experimental problems using the following rules. Each problem included two operators: multiplication and either addition or subtraction. For half of the problems within each type (congruent or incongruent spacing), multiplication was positioned on the left side of the expression, and addition (e.g., 3 * 5 + 7; four problems) or subtraction (e.g., 6 * 2 − 8; four problems) was positioned on the right side of the expression. For the other half of the problems, multiplication was positioned on the right side of the expression, and addition (e.g., 3 + 5 * 7; four problems) or subtraction (e.g., 6 − 2 * 8; four problems) on the left side of the expression. The numbers in each problem include one small (1, 2, or 3), medium (4, 5, or 6) and large (7, 8, or 9) one-digit value; each value was systematically varied in their position from the left to right (e.g., 2 * 4 + 7). The correct answer on all problems were integers ranging from −53 to 50. None of the problems were identical so students would not be able to recall an answer from a previous problem within the study (see Appendix A for the full list of problems).

We interleaved, rather than blocked, the congruent and incongruent problems to avoid the possibility that the participants might form a rule for using or ignoring the symbol spacing for the entire block of problems. Our rationale for using a predetermined, rather than a fully randomized, problem order were to (a) ensure that the same problem type (e.g., left multiplication operator position, incongruent spacing) did not appear consecutively for more than two trials, and (b) minimize potential between-subject variability as we addressed the primary goal of the original study—effects of spacing and inhibitory control on students’ arithmetic performance.

Approach to Analysis

Our approach to analysis was informed by prior findings from the experiment demonstrating students’ high performance across problems (Closser et al., 2023). In the initial analyses, we found that students’ accuracy for congruent (M = .94, SD = .08) and incongruent (M = .94, SD = .07) problems was consistently high with low variance. Furthermore, students took an average of 5.52 seconds to answer each problem, suggesting that they followed the instructions to quickly solve the problems. They took slightly longer to provide a correct response to congruent (M = 5.63 seconds, SD = 1.35) vs. incongruent problems (M = 5.41 seconds, SD = 1.48). To further explore the potential effect of operator positions and the unexpected spacing effect contrary to the existing research, we observed students’ problem-solving response time as our focal variable in the current analysis. Although the previously reported findings focused on outcomes at the student level (i.e., average accuracy, median response time), here we used problem-level outcomes (i.e., problem response time) to detect any potential nuanced effects of study stimuli and design choices on students’ performance. 

It is important to acknowledge that the distribution of response time data often follows an exponential decay curve (e.g., most response times are low with a small number of larger response times creating a tail in the distribution). As this may violate normality assumptions of traditional linear regression models, we examined these distributions in a preprocessing step to test for normality. The response time measures were found to violate normality assumptions for inclusion in linear regression models, so we applied a log transform to these measures before standardizing them using z-scoring for all reported analyses.

The approach to analysis for Research Question 1 and Research Question 2 follow our pre-registration with the exception of excluding an intercept in the analyses to aid interpretation (see Appendix B for the preregistered analyses including an intercept). Additionally, the results from the analysis for Research Question 2 prompted us to conduct an exploratory analysis that was not pre-registered and is described below. 

Research Question 1: Effects of Higher-Order Operator Position

To address Research Question 1, we conducted a regression analysis in conjunction with a bootstrap-sampling method. The regression analysis observed the response time of the sampled problem for each student as the dependent variable. As independent variables, we observed the position of the multiplication operator (left or right) while also accounting for the specific problem that was sampled (the problem identifier) as a dummy-coded categorical variable, included as a fixed effect. Because the problems systematically varied in congruent vs. incongruent spacing and previous research has demonstrated the spacing effect on students’ performance, we included the spacing type of the current problem represented as a dummy-coded variable. Since we included problem identifiers as a fixed effect, we ran our regression analysis without calculating an intercept (i.e. Eisenhauer, 2003); the positive problem indicator took the place of the intercept for each sample, allowing us to examine the coefficients of each of our variables of interest relative to each other rather than to a reference category. Given that prior research has shown minimal difference in results interpretation when incorporating group-level variables as fixed effects versus random intercepts, provided that group-level variance is adequately addressed through one of these methods (Closser et al., 2024), our choice to account for problem-level effects through fixed effects is further justified.

We implemented a bootstrap-sampling method (i.e., a method of repeating a sampling-with-replacement process and then averaging results over all iterations) because students in the study experienced all of the problems in the same order and the order of the problems may interact with shared variance at the student level when observing problem-level covariates. Accounting for such effects across all problems completed by all participants within a regression analysis would be difficult due to the confounding nature of student- and problem-level measures; alternative approaches, such as a repeated measures analysis using a multi-level model, may help account for some of these confounders but also imposes distributional assumptions over the variables and relationships that are not necessary when using bootstrapping (Lunneborg and Tousignant, 1985). For this reason, we used bootstrapping to account for sequence-based confounders by randomly sampling a single problem for each student to conduct a regression analysis. The process was then repeated, sampling with replacement, such that we replicated our analysis 1,000 times where each individual analysis observed only one problem per student. For each sample, each student problem had equal likelihood of being selected for inclusion in the respective regression, then the sampled data was filtered down to include only problems that were answered correctly. We focused on the problems to which students responded correctly and excluded the problems to which students responded incorrectly (average 6% of problems across students) in order to accurately capture the effects of operator position on students’ problem-solving response time. Averaging the results of this regression analysis over all 1,000 iterations provided mean estimates of coefficients for our independent variables of interest as well as confidence bounds for such estimates (for hypothesis testing, as per any traditional regression analysis). By incorporating randomization into this sampling method, the impact of the problem order was removed without necessitating more complex model structures or additional modeling assumptions.

Research Question 2: Sequence Effects

To address Research Question 2, we observed random problem pairs from each student. We observed response time on the second problem in the sampled pair as our dependent variable and the spacing sequence represented as a dummy-coded categorical variable. For example, if the first problem in the pair was an incongruent (IC) spacing problem and the second was congruent (C), this sequence was represented as “IC-C”, with all other combinations represented following the same convention (C-C (congruent problem followed by congruent problem; n=5), IC-IC (incongruent problem followed by incongruent problem; n=6), C-IC (congruent problem followed by incongruent problem; n=10), IC-C (incongruent problem followed by congruent problem; n=10)). We also controlled for the response time on the first problem in the pair and the specific problem pair as a fixed effect (e.g., for the pair of Problems 2 and 3, the pairing of 2-3 was represented as a dummy-coded categorical variable and included in the model as a fixed effect). As the focus of the analysis, we observed how the response time on the latter problem in the pair varied across the four different spacing sequence categories (i.e., IC-C, C-C, C-IC, IC-IC). 

We followed a similar regression- and bootstrapping-based approach as in Research Question 1, but sampled pairs of problems, rather than individual problems, for each student. For each bootstrapping sample, each pair of problems within each student had equal likelihood of being selected for inclusion in the respective regression, then the sampled data were filtered down to include only those selected pairs where both problems were answered correctly. We again fit the regression model without an intercept to make more direct and interpretable comparisons between our variables of interest.

Exploratory Analysis

In addition to our pre-registered analysis plan, we conducted a set of exploratory analyses to examine whether the inclusion or exclusion of problem and problem pair identifiers as a fixed effect in the models affected the coefficient estimates and interpretation of results. We rationalized that there may be unique aspects of each problem that could interact with, or confound, our variables of interest in unexpected ways. As there are a relatively small number of problems in the study and all students viewed the problems in the same order, we initially decided to include the problem identifiers as fixed effects rather than attempt to estimate clustered variance at a problem-level using random effects. For the exploratory analysis, we used a stepwise regression approach and re-introduced an intercept into each of the regression models but removed the problem and problem pair identifiers corresponding with the analyses for RQ1 and RQ2, respectively. If we were to find notable differences in the results after removing problem and problem pair identifiers, this would suggest that the results may be partially dependent on problem-level attributes beyond those that are accounted for by the higher-order operator position and sequence of spacing congruency. 

Results

The results of each analysis are described in alignment to each of our research questions. Although our choice to use log and z-score transformations on our dependent response time variables should be considered when interpreting the reported regression coefficients, we also present a format of our results that apply an inverse transformation to allow for comparisons of estimates in seconds.

Research Question 1: Effects of Operator Position

Note: CI: confidence interval. (s): seconds. The right-most columns provide an inverse transformation of the coefficient estimates as a measure of seconds to contrast the standardized coefficients reported in the left-most columns. Problem identifiers were also included as covariates in the regression but were excluded from this table to maintain the conciseness of the table.

Table 1 reports the results of the bootstrapped regression analysis to address our first research question regarding operator position. From this table, we see that all variables were found to be statistically significant predictors of response time. Lower values of response time indicate a faster response and the reported coefficients are standardized in the left of Table 1; the right side of the table reports the same coefficients and 95% confidence intervals for each variable with an inverse set of transforms applied so as to compare each in measures of seconds. 

The results indicate that when multiplication was on the left side of the expression, students exhibited faster response times than when the multiplication was on the right. The coefficient of -0.205 equates to response times that were approximately 0.97 seconds faster than when multiplication was on the right side of the expression (i.e., comparing 4.94 seconds when multiplication is on the left to 5.91 seconds when on the right). Similarly, when controlling for multiplication operator position, students were faster when the problem presented incongruent as opposed to congruent spacing, replicating the prior results (Closser et al., 2023). 

Although not the focus of this study, we acknowledge that the regression model issued convergence warnings in estimating the incongruent and congruent spacing variables due to issues of identifiability while controlling for all other factors. Although we are able to conclude that students exhibited faster response times on problems with incongruent versus congruent spacing, we cannot make strong claims in regard to the magnitude of this difference.

Research Question 2: Effects of Problem Sequencing

Note: CI: confidence interval. (s): seconds. The right-most columns provide an inverse transformation of the coefficient estimates as a measure of seconds to contrast the standardized coefficients reported in the left-most columns. Problem pair identifiers were also included in the regression but were excluded from this table.

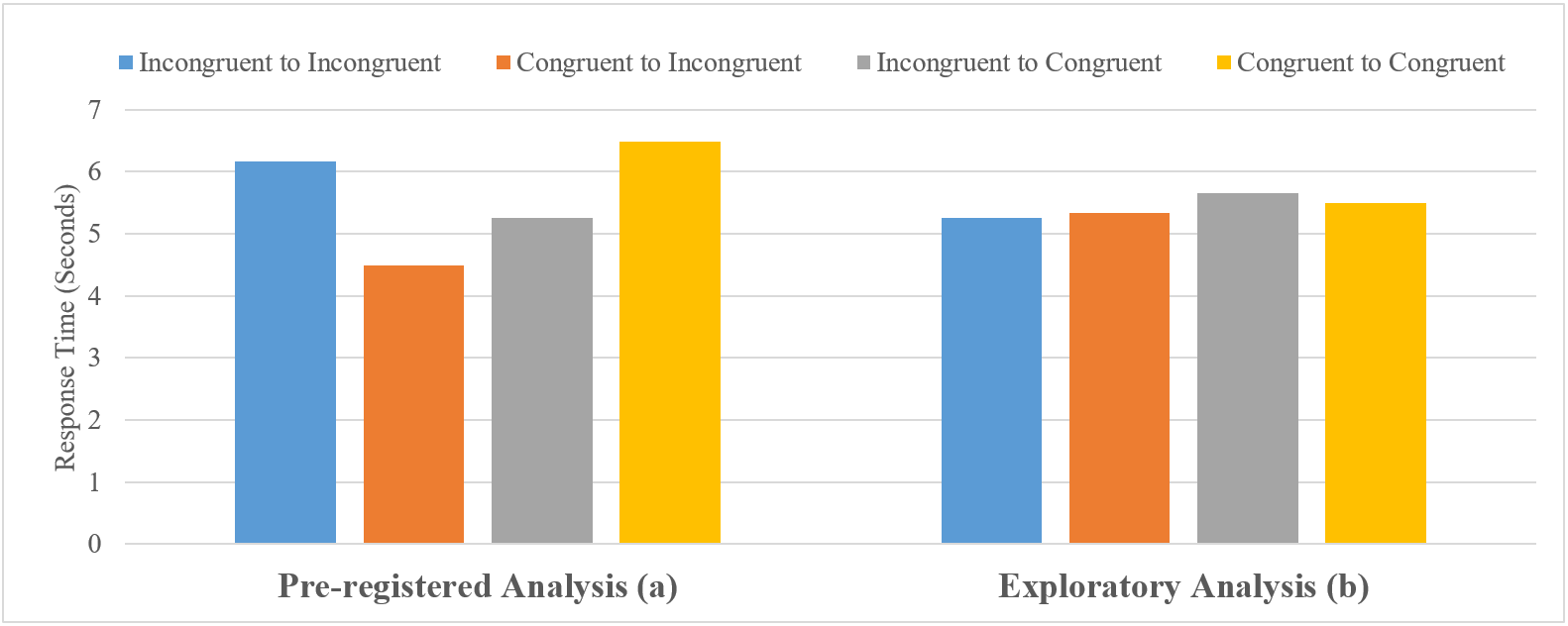
Table 2 reports the results of the bootstrapped regression analysis to address our second research question regarding sequencing effects. With the removal of an intercept, statistical significance (at p < .05) can be determined by non-overlapping 95% confidence intervals. All of the variables emerged as statistically significant predictors of student response time. As to be expected, students with slower response times on the first problem of the sampled problem pair exhibited slower response times on the subsequent problem. In observing the four categories describing the spacing sequence over the pair, transitioning from congruent to incongruent (C-I) spacing correlated with the fastest response times. Conversely, students exhibited the slowest response times when exposed to congruent-to-congruent (C-C) problem sequencing. The comparison of these response times across each of the spacing sequence categories is illustrated in Figure 1a.

Exploratory Analysis Results

Removing the problem identifiers and re-introducing an intercept to the regression analysis to address our first research question led to similar results and interpretations as the original analysis. When the multiplication operator was on the left, students exhibited faster response times as compared to when the operator was on the right. Additionally, the same effects of congruent spacing emerged in this analysis as those reported above: students exhibited faster response times on problems with incongruent, as compared to those with congruent, spacing. These similarities indicate that the inclusion or exclusion of problem identifiers as fixed effects had a low impact on the results and no impact on our interpretation (see details in Appendix C).

However, in the exploratory analysis addressing our second research question, there were notable differences when removing the problem pair identifiers and re-introducing an intercept to the regression; this is illustrated in Figure 1b. Although, rather unsurprisingly, prior response time maintained the same positive relation with response time on the second problem in the pair, the effects of congruency sequence did change. When the problem identifiers were removed, the incongruent-to-incongruent (IC-IC) spacing sequence category was associated with the fastest response times. Conversely, the incongruent-to-congruent (IC-C) category exhibited the slowest response times.

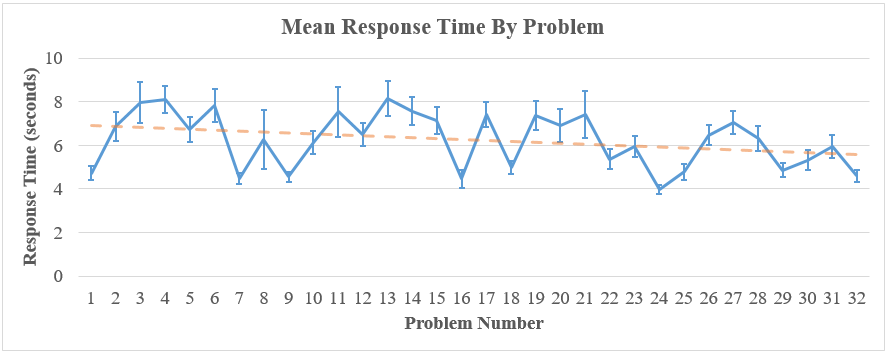
Given that there were seven congruent problems in the first half of the task and nine congruent problems in the second half of the task, the slower response time observed on congruent problems might have been associated with student fatigue over time and the problem order within the task. This speculation was not supported by Figure 2 which visualizes the average response time per problem. Contrary to the speculation, there is a slight trend toward faster response times on later trials, but this trend is not statistically significant, suggesting that problem order could not explain the pattern of results on symbol spacing.

Discussion

Although a large body of evidence has suggested that children and adults alike are susceptible to the influence of perceptual cues created by altering the space between symbols in mathematics notation (Braithwaite et al., 2016; Harrison et al., 2020; Landy and Goldstone, 2007a; 2010; Rivera and Garrigan, 2016), our previous finding on undergraduates’ problem-solving accuracy and average response time did not replicate the effects of spacing cues (Closser et al., 2023). That discrepancy prompted us to explore the data from Closser et al. (2023) at the problem level to analyze how the (a) higher-order operator position, and (b) sequential order of experimental problems, might have impacted students’ performance. Three main findings emerged. First, undergraduates displayed faster response times on problems that showed the multiplication operator on the left, rather than right, side of the expression. Second, students varied in average response times based on the spacing sequence between two problems, suggesting that sequencing mattered. Third, accounting for or excluding problem pair identifiers in analyses changed the interpretation of results, suggesting that the effect of sequencing might be impacted by other problem-level factors. Together, these results suggest that aspects of the materials and study design had nuanced effects on undergraduates’ performance. In the following sections, we discuss plausible explanations for these findings, their contributions to research on perception, cognition, and learning, and their implications for education research conducted with mathematics content. 

Effects of Operator Location: Solving from Left to Right

Consistent across all analyses, undergraduate students demonstrated significantly faster response times when simplifying expressions with the multiplication operator in the left-, rather than right-hand, position. On average, participants were approximately a second quicker to simplify expressions with the multiplication operator positioned on the left vs. on the right. Relative to the average response time around five seconds, the results suggest that there is a 16% reduction in students’ problem-solving time when exposed to problems with the higher-order operator positioned on the left versus right. This finding supported our hypothesis as well as prior work (e.g., Bye et al., 2022; Kieran, 1979; Linchevski and Livneh, 1999; Ngo et al., 2023; Norton and Cooper, 2001). Furthermore, these findings are well-aligned with a body of evidence showing that students tend to start performing arithmetic calculations from left to right in childhood and continue using this strategy even when it may be invalid or inefficient down the road in arithmetic or algebra.

This behavior (simplifying from left to right) displayed at the undergraduate level may be partially attributed to students’ early experiences in mathematics education. Although unintended, facets of early mathematics education in the U.S. incidentally promote the misconception that mathematics is a series of calculations to be performed from left to right (like reading in English), culminating when students reach the equals sign as their cue to “calculate” or “total” the terms (e.g., 5 + 2 = __; McNeil et al., 2006). Consequently, these operational routines become ingrained in students’ understanding of mathematics early on and make students more resistant to changing their problem-solving strategies and interpretation of concepts like the equals sign (McNeil, 2008). McNeil and Alibali (2005) demonstrated this connection between students’ problem-solving behavior and knowledge in elementary school as well as at the undergraduate level. Specifically, they found that elementary students’ with a stronger adherence to operational patterns of solving arithmetic problems (e.g., performing all operations on all numbers within an equation) were less likely to learn from a lesson on equations. To take this a step further, they then manipulated whether undergraduates’ knowledge of these operational patterns was activated. They found that those whose knowledge of the operational patterns was activated were less likely to use correct equation-solving strategies, demonstrating the hindrance of operational patterns of problem solving. In sum, this body of work demonstrates how students’ performance on basic arithmetic equations can be influenced by, and reflect, their knowledge of incorrect strategies that were likely accrued in elementary school.

Here, we posit that one plausible explanation for students’ tendency to solve problems quicker when they could perform calculations from left to right is that this strategy is entrenched in students’ problem-solving routines from years of experience. This finding is particularly interesting given the sample and mathematics content: college students’ problem-solving speed was impacted by operator position even though they were facing content taught in elementary and middle school. This result suggests that the left-to-right solving strategy may persist into adulthood even for learned skills in mathematics (i.e., simplifying order of operations expressions). Given that repeated practice opportunities in online settings increase students’ problem-solving accuracy (Koedinger et al., 2023), these findings with college students suggest that online instructional content should include a variety of problem formats with different higher-order operator position so that students receive sufficient practice and feedback beyond the left-to-right calculation format.

There may also be some sort of interaction between students’ tendency to simplify expressions from left to right and their tendency to use the higher-order operator as a perceptual cue to direct their attention when simplifying expressions. Landy et al. (2008) have found, through an eye-tracking study, that undergraduate students fixated sooner and longer on multiplication operators than addition operators, suggesting students’ tendency to attend to the higher-order operator. Furthermore, Egorova et al. (in press) found that undergraduates were quicker to fixate on the higher-order operator when it was on the left side, instead of center or right side, of expressions, suggesting the influence of the position of the higher-order operator. Their participants were also more accurate and quicker to respond on these items, consistent with our finding that participants were faster to correctly respond to problems with the multiplication operator on the left, instead of right, side of the expression. Together, these findings support the theory that students use the higher-order operator as a perceptual cue to guide their attention in expressions, and their performance benefits from viewing expressions with the higher-order operator positioned on the left. 

These findings have implications for educational researchers to take into consideration when designing experimental or instructional arithmetic problem sets for students. In particular, materials should include expressions or equations that strategically vary the position of the higher-order operator. Researchers should also account for the validity of left-to-right calculations in data analysis. Furthermore, these findings directly prompt future educational research. If undergraduates display rigid problem-solving strategies that may have emerged earlier in their formal education experience (such as performing calculations from left to right), future studies should employ a developmental approach to investigate whether and how students’ problem-solving strategies shift across age and contexts, and the role of perceptual problem features over time. Learning technologies may be able to provide large-scale cross-sectional data to compare student performance on online activities with varied problem features across different ages and/or grade levels.

Effects of Sequencing and Nuanced Problem Features

Compared to the robust and consistent effect of operator position, the priming effects of symbol spacing as examined through the problem sequence was less clear. To determine whether the sequential order of problems impacted students’ performance, we investigated how response times varied when students transitioned between problems with congruent and/or incongruent spacing. Our primary results (including problem identifiers as a fixed effect) show that students displayed the fastest response times when transitioning from congruent to incongruent (C-IC) spacing problems. Conversely, students displayed the slowest response times when transitioning from congruent to congruent (C-C) spacing problems. However, in our exploratory analysis (excluding the problem identifiers), we found that students displayed the fastest response times when transitioning from problems with incongruent to incongruent (IC-IC) spacing, and the slowest response times when transitioning from problems with incongruent to congruent (IC-C) spacing. 

The exploratory finding somewhat aligns with our initial hypotheses grounded in the negative priming literature (Frings et al., 2015; Neill, 1997): students’ response times may be the slowest when solving congruent problems immediately after solving incongruent problems and the quickest when they transition between problems with the same type of perceptual cues. These sequencing effects, however, do not persist when we include the problem identifier in our primary analysis, suggesting that these effects may not be robust and other problem factors may be at play. Given the inconsistent findings, we are reluctant to conclude that the sequence of problems may explain the unexpected results of slower response time on problems with congruent vs. incongruent spacing reported by Closser et al. (2023). Nevertheless, the current findings offer some practical considerations for research.

As we found no differences in interpretation for our first research question when including (primary analysis) vs. excluding problem identifier (exploratory analysis), it is unlikely that content-related confounders alone impacted the results. Instead, we see differences between our primary and exploratory results only regarding those analyses addressing our second research question on sequencing effects. As there were slightly more congruent problems in the second half of the task (nine problems) compared to the first half (seven problems), student fatigue is one potential explanation for the slower response times when transitioning to congruent problems. However, plotting the overall mean response times by problem showed that response times varied by problem with no evidence of fatigue across the duration of the experiment. Instead, there was a slight overall trend toward faster response times from start to finish of the task. Such a trend may conversely indicate learning, offering another potential explanation for the difference between our pre-registered and exploratory results. However, this trend is not statistically significant so there is insufficient evidence to conclude that either fatigue or unmeasured learning are attributable to our findings.

The findings suggest that aspects of the problem (that are not measured here) impact the relations between the spacing sequences and student response times. These unmeasured aspects may include, for example, differences in problem difficulty or interactions between the magnitude, position, or combination of numbers within each problem. In this study, it is difficult to tease apart the impact of these factors as all students experienced the same problems in the same order and the study included a limited number of problems for analysis. Therefore, it is unclear whether these results would replicate in other contexts with a different set or ordering of problems. However, it is clear that research on perceptual learning in mathematics, and other interdisciplinary research on mathematics problem solving, should consider the affordances and challenges of using a within-subjects study design. Furthermore, whether using experimental or naturalistic data from online settings, researchers should consider analysis choices that account for unintended effects of mathematics content such as the problem features and ordering.

Critically, if the primary results reported in Closser et al. (2023) had aligned with related work and our hypotheses, we likely would not have thought to investigate nuanced effects of problem features at the problem level. The current results highlight the necessity of being wary of drawing conclusions from relatively small datasets, particularly when minute, unmeasured factors might influence the results. In sharing this narrative, we demonstrate how applying EDM approaches to experimental datasets can supplement primary analyses and delineate potential effects of study design choices to draw more accurate conclusions about student behavior, performance, and learning. Especially since EDM is commonly applied to data from naturalistic settings, not necessarily experimental data, this study serves as an interdisciplinary example of how EDM methods can help researchers in related fields probe vast amounts of data to investigate causal effects, or limitations of causal inference, beyond traditional quantitative analyses.

Limitations

This study had two main limitations that may guide decisions in future research. First, the study only included 32 experimental problems completed by a relatively narrow sample of students. The small sample size at the problem level limited our ability to reliably estimate the effects in the current analyses. Similarly, the students included in the sample were all high performing, with little variance in accuracy and response time. It is unsurprising that there was little variance in undergraduates’ performance on arithmetic content as that content is likely to be covered in elementary and middle school mathematics education. The original intention of the experiment was to detect spacing effects that were not contingent on the problem difficulty; however, the limited variance in performance restricted our ability to detect effects of problem features. We also note that using the participant pool of students from a private university limits the generalizability of these results. However, using such samples is typical in psychological research. This project demonstrates how educational data mining methods, such as bootstrapping, can supplement data analysis for online experiments and, conversely, how experimental data can inform analysis decisions with educational data from similar contexts.

Second, all participants saw the predetermined randomized sequence of problems in the same order, which is a common practice in classrooms and some research studies. However, as opposed to presenting problems in a completely randomized order unique to each student, this approach might have created some bias in our study (Čechák and Pelánek, 2019). As shown through the series of analyses including vs. excluding problem pair identifiers as a fixed effect, the particular problems and their order within the study likely influenced the pattern of results. In designing the experiment, we had intentionally counterbalanced the multiplication position across problems, the use of addition vs. subtraction operators, and the magnitude of each one-digit number used in the problems. Although we specifically accounted for problem identity and order in the current analysis, using a predetermined problem sequence limits the conclusions we are able to draw. It is possible that these or other problem features not examined or modeled in the current analyses explain the pattern of results we observed. With only a small number of experimental problems, we were not able to account for all of the possible effects of problem features and ordering. The outcomes of this study design do align with simulated experiments demonstrating item ordering biases (Čechák and Pelánek, 2019) and provide an example of item ordering biases using real student data from an online experiment.

Implications for Future Research and Education

Based on these limitations, future studies aimed at investigating the effects of perceptual features within mathematics problems should include more problems with a variety of structure (e.g., problems varying in number magnitude and composition) and fully randomize the problem order for each participant. Additionally, modifying the study stimuli or diversifying the study sample so that participants are more challenged by the mathematics content should provide more variance in the data. Doing so will provide additional insights into whether, when, and how much these seemingly irrelevant features impact students’ performance on mathematics problems.

The current study does not directly provide implications for educational practice but does provide methodological guidelines on how to design and test online instructional materials for K-12 mathematics education. Here, we measured participants’ response times on a single-session experiment with no intention of seeing improvement since participants never received any instructional support or performance feedback. The results show that nuanced problem features do impact students’ response times; therefore, such features should at least be controlled for when designing and testing educational materials in online settings to appropriately support causal inference related to student performance.

As more education research is conducted in online learning platforms, performance metrics such as response times can serve as proxies for constructs that go beyond correctness to capture performance across different time scales (e.g., Chan et al., 2022a), such as procedural fluency, a major goal in national mathematics education in the U.S. (Swafford and Kilpatrick, 2002; Loewenberg, 2003). Looking ahead, these results will inform our methodology to develop and test online mathematics materials for K-12 education that use perceptual cues in worked examples as a form of scaffolding to support math learning in earlier grades. More broadly, educational researchers investigating students’ behavior, mathematics performance, or learning from online log files should consider using design and analysis choices that acknowledge the effects of operator position, problem sequencing, and other nuanced features that might not be the focus of research but could impact results and interpretation.

Finally, as the field pushes towards creating solutions for education that leverage artificial intelligence, this project exemplifies how students’ online problem-solving performance is driven by interactions that are interpretable by human researchers but remain too complex for artificial intelligence systems that are unable to connect educational data with students’ sensorimotor experiences and sociocultural contexts (Nathan, 2023). Echoing Nathan (2023), it is critical to augment automated and artificial intelligence solutions for education with human interpretation, necessitating interdisciplinary approaches that intertwine human sense-making and computational advances to understand student behavior. For example, the EDM methods here allow us to bootstrap the sample and model the dataset in various ways fairly quickly; however, human judgments are needed to determine appropriate analytical methods and interpret results based on theory and an understanding of the context in which the study is situated.

Conclusion

This manuscript describes a pre-registered analysis plan that leveraged EDM techniques, specifically a bootstrapping sampling method with regression analysis, to investigate the effects of problem-level features that may explain undergraduate students’ performance simplifying arithmetic expressions in an online experiment. We found that students were consistently quicker to correctly simplify expressions when they could perform calculations from left to right, conceptually replicating prior research demonstrating students’ left-to-right solving bias in mathematics. Furthermore, the order in which students viewed problems affected their performance, and other problem features unaccounted for in the current analyses might have also impacted performance. These findings indicate that research on problem solving and perceptual learning in mathematics should deliberately balance, and control for, features of study stimuli that could inadvertently affect outcome variables. These features may include the operator positions within problems and the sequential order of problems across an experiment. Namely, we recommend that future related research (a) includes problems that vary in composition and other characteristics, as well as (b) randomizes the problem order or leverages study design and data analysis approaches to systematically investigate these variables. Following these guidelines, researchers should also apply similar approaches with existing data in online platforms to inform mathematics education research and the development of tools that effectively improve students’ mathematics problem solving.

Acknowledgments

The research reported here was supported, in part, by the Institute of Education Sciences, U.S. Department of Education, through grant R305N230034 to Purdue University, the National Science Foundation (#2331379), and Schmidt Futures. The opinions expressed are those of the authors and do not represent the views of the Institute of Education Sciences or the U.S. Department of Education.

References

1. Abrahamson, D. and Trninic, D. 2015. Bringing forth mathematical concepts: Signifying sensorimotor enactment in fields of promoted action. ZDM Math Education 47, 295–306. doi: 10.1007/s11858-014-0620-0
2. Alibali, M. W., Crooks, N. M., and McNeil, N. M. 2018. Perceptual support promotes strategy generation: Evidence from equation solving. British Journal of Developmental Psychology 36, 153–168. https://doi.org/10.1111/bjdp.12203
3. Baker, R. S. J. d., Gowda, S. M., Corbett, A. T., and Ocumpaugh, J. 2012. Towards Automatically Detecting Whether Student Learning is Shallow. In Intelligent Tutoring Systems: 11th International Conference. S. A. Cerri, J.C. William, G. Papadourakis, and K. Panourgia, Eds. Springer Berlin Heidelberg, 444-453.
4. Beck, J. E. and Mostow, J. 2008. Improving the Educational Value of Intelligent Tutoring Systems through Data Mining. Frontiers in Artificial Intelligence and Applications, 158, 421.
5. Booth, J. L., McGinn, K. M., Barbieri, C., Begolli, K. N., Chang, B., Miller-Cotto, D., Young, L.K. and Davenport, J. L. 2017. Evidence for cognitive science principles that impact learning in mathematics. In Acquisition of Complex Arithmetic Skills and Higher-order Mathematics Concepts, D. C. Geary, D. B. Berch, R. Ochsendorf, and K. M. Koepke, Eds. Academic Press, 297-325.
6. Botelho, A. F., Varatharaj, A., Patikorn, T., Doherty, D., Adjei, S. A., and Beck, J. E. 2019. Developing Early Detectors of Student Attrition and Wheel Spinning Using Deep Learning. Journal of IEEE Transactions on Learning Technologies 12, 2, 158-170. doi: https://doi.org/10.1109/TLT.2019.2912162
7. Botelho, A. F., Adjei, S. A., Bahel, V., and Baker, R. S. 2022. Exploring Relationships Between Temporal Patterns of Affect and Student Learning. In Proceedings of the 30th International Conference on Computers in Education, Iyer, S. et al., Eds., AsiaPacific Society for Computers in Education,139-144.
8. Braithwaite, D. W., Goldstone, R. L., van der Maas, H. L. J., and Landy, D. H. 2016. Non-formal mechanisms in mathematical cognitive development: The case of arithmetic. Cognition 149, 40–55.
9. Butler, A. C., Marsh, E. J., Slavinsky, J. P., and Baraniuk, R. G. 2014. Integrating cognitive science and technology improves learning in a STEM classroom. Educational Psychology Review 26, 2, 331-340.
10. Bye, J., Lee, J. E., Chan, J. Y. C., Closser, A. H., Shaw, S., and Ottmar, E. 2022. Perceiving precedence: Order of operations errors are predicted by perception of equivalent expressions [Poster]. Presented at the 2022 Annual Meeting of the American Educational Research Association (AERA).
11. Carvalho, P. F. and Goldstone, R. L. 2014. Putting category learning in order: Category structure and temporal arrangement affect the benefit of interleaved over blocked study. Memory & Cognition 42, 3, 481-495.
12. Chan, J. Y.-C., Ottmar, E., and Lee, J.-E. 2022a. Slow down to speed up: Longer pause time before solving problems relates to higher strategy efficiency. Learning and Individual Differences 93, 102109. DOI: 10.1016/j.lindif.2021.102109
13. Chan J. Y.-C., Ottmar, E. R., Smith, H., and Closser, A. H. 2022b. Variables versus numbers: Effects of symbols and algebraic knowledge on students’ problem-solving strategies. Contemporary Educational Psychology 71, 102114. DOI: 10.1016/j.cedpsych.2022.102114
14. Chan, J. Y.-C., Sidney, P. G., and Alibali, M. W. 2019. Corresponding color coding facilitates learning of area measurement. In Proceedings of the 41st annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA 2019). S. Otten, A. G. Candela, Z. de Araujo, C. Haines, and C. Munter, Eds. North American Chapter of the International Group for the Psychology of Mathematics Education - North American Chapter, 222-223.
15. Chase, W. G. and Simon, H. A. 1973. Perception in chess. Cognitive Psychology 4, 1, 55-81.
16. Čechák, J., and Pelánek, R. 2019. Item ordering biases in educational data. In Artificial Intelligence in Education: 20th International Conference, AIED 2019. Isotani, S., Millán, E., Ogan, A., Hastings, R., McLaren, B., and Luckin, R., Eds. Chicago, IL, USA, June 25-29, Proceedings, Part I 20, Springer International Publishing, 48-58.
17. Closser, A. H., Chan, J. Y.-C., and Ottmar, E. 2023. Resisting the urge to calculate: The relation between inhibition skills and perceptual cues in arithmetic performance. Quarterly Journal of Experimental Psychology 76, 12, 2690-2703. https://doi.org/10.1177/17470218231156125
18. Closser, A. H., Chan, J. Y.-C., Smith, H., and Ottmar, E. R. 2022. Perceptual learning in math: Implications for educational research, practice, and technology. Rapid Community Report Series. Digital Promise and the International Society of the Learning Sciences. https://repository.isls.org//handle/1/7668
19. Closser, A. H., Sales, A. C., and Botelho, A. F. 2024. Should we account for classrooms? Analyzing online experimental data with student-level randomization. Educational Technology Research and Development. https://doi.org/10.1007/s11423-023-10325-x
20. Ebbinghaus, H. 1913. Memory: A contribution to experimental psychology. New York, NY: Teachers College, Columbia University.
21. Egorova, A., Ngo, V., Liu, A., Mahoney, M., Moy, J., and Ottmar, E. In press. Math presentation matters: How superfluous brackets and higher order operator position in mathematics can impact problem solving. In press at Mind Brain and Education.
22. Eisenhauer, J. G. 2003. Regression through the origin. Teaching Statistics 25, 3, 76-80.
23. Frings, C., Schneider, K. K., and Fox, E. 2015. The negative priming paradigm: An update and implications for selective attention. Psychonomic Bulletin and Review 22, 6, 1577-1597.
24. Gibson, E. J. 1969. Principles of perceptual learning and development. East Norwalk, CT: Appleton-Century-Crofts.
25. Gibson, J. J. 1970. The ecological approach to visual perception. Boston: Houghton-Mifflin.
26. Givvin, K. B., Moroz, V., Loftus, W., and Stigler, J. W. 2019. Removing opportunities to calculate improves students’ performance on subsequent word problems. Cognitive Research: Principles and Implications 4, 1, 1–13.
27. Goldstone, R. L., Marghetis, T., Weitnauer, E., Ottmar, E. R., and Landy, D. 2017. Adapting perception, action, and technology for mathematical reasoning. Current Directions in Psychological Science 26, 5, 434-441.
28. Gurung, A., Botelho, A. F., and Heffernan, N. T. 2021, April. Examining Student Effort on Help through Response Time Decomposition. In Proceedings of the 11th International Conference on Learning Analytics and Knowledge. ACM. 292-301.
29. Harrison, A., Smith, H., Hulse, T., and Ottmar, E. 2020. Spacing out!: Manipulating spatial features in mathematical expressions affects performance. Journal of Numerical Cognition 6, 2, 186-203. https://doi.org/10.5964/jnc.v6i2.243
30. Higgins, E. J., Dettmer, A. M., and Albro, E. R. 2019. Looking back to move forward: a retrospective examination of research at the intersection of cognitive science and education and what it means for the future. Journal of Cognition and Development 20, 2, 278-297.
31. Jiang, M. J., Cooper, J. L., and Alibali, M. W. 2014. Spatial factors influence arithmetic performance: The case of the minus sign. Quarterly Journal of Experimental Psychology 67, 8, 1626-1642.
32. Kieran, C. 1979. Children’s operational thinking within the context of bracketing and the order of operations. In Proceedings of the 3rd Conference of the International Group for the Psychology of Mathematics Education. Tall, D. Ed. Warwick, UK: PME, 128–133.
33. Koedinger, K. R., Carvalho, P. F., Liu, R., and McLaughlin, E. A. 2023. An astonishing regularity in student learning rate. Proceedings of the National Academy of Sciences 120, 13, e2221311120. https://doi.org/10.1073/pnas.2221311120
34. Koedinger, K. R., McLaughlin, E. A., and Stamper, J. C. 2010. Automated Student Model Improvement. In Proceedings of the 5th International Conference on Educational Data Mining. Yacef, K., Zaiane, O., Hershkovitz, A., Yudelson, M., and Stamper, J., Eds. International Educational Data Mining Society, 17–24.
35. Kumar, D. 2021. Survey Paper on Information based Learning System using Educational Data Mining. International Journal for Research in Applied Science and Engineering Technology 10, 2, 518-522. https://doi.org/10.22214/ijraset.2021.35431
36. Landy, D. and Goldstone, R. L. 2007. How abstract is symbolic thought?. Journal of Experimental Psychology: Learning, Memory, and Cognition 33, 4, 720-733.
37. Landy, D. H. and Goldstone, R. L. 2010. Proximity and precedence in arithmetic. Quarterly Journal of Experimental Psychology 63, 10, 1953-1968.
38. Landy, D. H., Jones, M. N., and Goldstone, R. L. 2008. How the appearance of an operator affects its formal precedence. In Proceedings of the Thirtieth Annual Conference of the Cognitive Science Society. B. C. Love, K. McRae, and V. M. Sloutsky, Eds. Washington, DC: Cognitive Science Society. 2109–2114
39. Lee, J. E., Chan, J. Y. C, Botelho, A. F., and Ottmar E. R. 2022a. Does slow and steady win the race?: Clustering patterns of students’ behaviors in an interactive online mathematics game. Journal of Educational Technology Research and Development 70, 1575-1599. doi: https://doi.org/10.1007/s11423-022-10138-4
40. Lee, J. E., Hornburg, C. B., Chan, J. Y.-C., and Ottmar, E. 2022b. Perceptual and number effects on students’ initial solution strategies in an interactive online mathematics game. Journal of Numerical Cognition 8, 1, 166-182.
41. Li, N., Cohen, W. W., and Koedinger, K. R. 2013. Problem order implications for learning. International Journal of Artificial Intelligence in Education 23, 71-93.
42. Linchevski, L. and Livneh, D. 1999. Structure sense: The relationship between algebraic and numerical contexts. Educational Studies in Mathematics 40, 173-196.
43. Liu, Q. and Braithwaite, D. 2023. Affordances of fractions and decimals for arithmetic. Journal of Experimental Psychology: Learning, Memory, and Cognition 49, 9, 1459-1470. Advance online publication. https://doi.org/10.1037/xlm0001161
44. Loewenberg, D. (2003). Mathematical proficiency for all students: Toward a strategic research and development program in mathematics education. Rand Corporation.
45. Lunneborg, C. E. and Tousignant, J. P. 1985. Efron's bootstrap with application to the repeated measures design. Multivariate Behavioral Research 20, 2, 161-178.
46. Marghetis, T., Landy, D., & Goldstone, R. L. (2016). Mastering algebra retrains the visual system to perceive hierarchical structure in equations. Cognitive Research: Principles and Implications, 1, 1-10.
47. McNeil, N. M. 2008. Limitations to teaching children 2+ 2= 4: Typical arithmetic problems can hinder learning of mathematical equivalence. Child Development 79, 5, 1524-1537.
48. McNeil, N. M. and Alibali, M. W. 2005. Why won't you change your mind? Knowledge of operational patterns hinders learning and performance on equations. Child Development 76, 4, 883-899.
49. McNeil, N. M., Chesney, D. L., Matthews, P. G., Fyfe, E. R., Petersen, L. A., Dunwiddie, A. E., and Wheeler, M. C. 2012. It pays to be organized: Organizing arithmetic practice around equivalent values facilitates understanding of math equivalence. Journal of Educational Psychology 104, 4, 1109.
50. McNeil, N. M., Grandau, L., Knuth, E. J., Alibali, M. W., Stephens, A. C., Hattikudur, S., and Krill, D. E. 2006. Middle-school students' understanding of the equal sign: The books they read can't help. Cognition and Instruction 24, 3, 367-385.
51. Nathan, M. J. 2023. Disembodied AI and the limits to machine understanding of students’ embodied interactions. Frontiers in Artificial Intelligence 6, 1148227. https://doi.org/10.3389/frai.2023.1148227
52. Neill, W. T. 1977. Inhibition and facilitation processes in selective attention. Journal of Experimental Psychology: Human Perception and Performance 3, 444–450.
53. Neill, W. T. 1997. Episodic retrieval in negative priming and repetition priming. Journal of Experimental Psychology: Learning, Memory, and Cognition 23, 6, 1291.
54. Ngo, V., Perez, L., Closser, A. H., and Ottmar, E. 2023. The effects of operand position and superfluous brackets on student performance in math problem-solving. Journal of Numerical Cognition 9, 1, 107-128. https://doi.org/10.5964/jnc.9535
55. Norton, S. J. and Cooper, T. J. 2001. Students’ perceptions of the importance of closure in arithmetic: implications for algebra. In Proceedings of the International Conference of the Mathematics Education into the 21st Century Project, 19-24.
56. Ottmar, E. R., Landy, D., Goldstone, R., and Weitnauer, E. 2015. Getting From Here to There!: Testing the effectiveness of an interactive mathematics intervention embedding perceptual learning. In Proceedings of the Thirty-Seventh Annual Conference of the Cognitive Science Society, Pasadena, CA: Cognitive Science Society, 1793–1798.
57. Ostrow, K. S. and Heffernan, N. T. 2014. Testing the Effectiveness of the ASSISTments Platform for Learning Mathematics and Mathematics Problem Solving. In Proceedings of the 7th International Conference on Educational Data Mining. Stamper J., Pardos, Z., Mavrikis M., McLaren, B., Eds. London, U.K., International Educational Data Mining Society, 344–347.
58. Proctor, R. W. 1980. The influence of intervening tasks on the spacing effect for frequency judgments. Journal of Experimental Psychology: Human Learning and Memory 6, 3 (1980), 254–266. DOI: 10.1037/0278-7393.6.3.254
59. Rau, M. A., Mason, B., and Nowak, R. 2016. How to Model Implicit Knowledge? Similarity Learning Methods to Assess Perceptions of Visual Representations. In Proceedings of the 9th International Conference on Educational Data Mining. Barnes, T., Chi, M., and Feng, M., Eds. International Educational Data Mining Society, 199-206.
60. Rivera, J., and Garrigan, P. 2016. Persistent perceptual grouping effects in the evaluation of simple arithmetic expressions. Memory & Cognition 44, 5, 750-761.
61. Sen, A., Patel, P., Rau, M. A., Mason, B., Nowak, R., Rogers, T. T., and Zhu, X. 2018. Machine Beats Human at Sequencing Visuals for Perceptual-Fluency Practice. In Proceedings of the 11th International Conference on Educational Data Mining. Boyer, K., E., and Yudelson, M., Eds. International Educational Data Mining Society, 137-146.
62. Swafford, J., & Kilpatrick, J. (Eds.). (2002). Helping Children Learn Mathematics. National Academies Press.
63. Szokolszky, A., Read, C., Palatinus, Z., and Palatinus, K. 2019. Ecological approaches to perceptual learning: learning to perceive and perceiving as learning. Adaptive Behavior 27, 6, 363-388.
64. Wagemans, J., Elder, J. H., Kubovy, M., Palmer, S. E., Peterson, M. A., Singh, M., and von der Heydt, R. 2012. A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure-ground organization. Psychological Bulletin 138, 2012, 1172–1217.
65. Wertheimer, M. 1938. Gestalt theory. In A source book of Gestalt psychology. Ellis, W. D. Ed. Kegan Paul, Trench, Trubner & Company. 1–11. DOI: 10.1037/11496-001
66. Xinlin, Z. and Qi, D. 2003. Representation formats for addition and multiplication facts. Acta Psychologica Sinica 35, 3, 345-351.

Appendices

Appendix A: Experimental Problems

Note: Spacing Congruency denotes whether the problem spacing is either congruent or incongruent to the order of operations. Spacing Sequence refers to the transition from the previous problem type to the current problem type. 

Appendix B: Preregistered Results

This section presents the results of our preregistered analyses. The results reported in the manuscript follow the same analysis procedure but exclude the intercept from each regression model to allow for more direct comparisons between our variables of interest rather than with respect to a reference category. These results examine whether the modeling choice to remove the intercepts from the regression analyses has any impact on the interpretation of our results. As problem identifiers and problem-pair identifiers are included in each of the analyses within this section, the exclusion of an intercept should have no meaningful impact on our results. The results reported in this Appendix confirm this claim.

Research Question 1: Effects of Operator Position

Note: (CI): confidence interval. (s): seconds. The right-most columns provide an inverse transformation of the coefficient estimates as a measure of seconds to contrast the standardized coefficients reported in the left-most columns. Problem identifiers were also included in the regression but were excluded from this table.

Table B1 reports the results of the bootstrapped regression analysis to address our first research question. All variables were found to be statistically significant predictors of response time. As a reminder for this analysis, lower values of response indicate a faster response and the reported coefficients are standardized. It is also important to acknowledge, for interpretation, that the response time dependent variable was adjusted using a log transform before z-scoring. When multiplication was on the left side of the expression, students exhibited faster response times. When controlling for multiplication placement, students were also faster when the problem contained incongruent spacing as opposed to congruent spacing. These findings are consistent with the reported primary analysis, confirming that the exclusion of an intercept has no impact on the results or our interpretation.

Research Question 2: Effects of Sequencing

Note: (CI): confidence interval. (s): seconds. The right-most columns provide an inverse transformation of the coefficient estimates as a measure of seconds to contrast the standardized coefficients reported in the left-most columns. Problem pair identifiers were also included in the regression but were excluded from this table.

The result of the bootstrapped regression analysis to address our second research question is reported in Table B2. All variables emerged as significant predictors of response time. Unsurprisingly, there was a positive relation between response time on the first problem and response time on the second problem within the pair. We find that students exhibited the slowest response times when working on a congruent problem that was preceded by a congruent problem. Conversely, students exhibited the fastest response times on an incongruent problem that was preceded by a congruent problem. These findings are consistent with the reported primary analysis, confirming that the exclusion of an intercept has no impact on our results.

Appendix C: Exploratory Results

Our exploratory analysis examines whether the exclusion of problem and problem pair identifiers from each of our regression models impacts the interpretation of our results. As students in the study were given the same limited set of problems in the same order, this analysis helps identify whether our analyses may be sensitive to the specific content and ordering used in the study.

Research Question 1: Effects of Operator Position

Note: (CI): confidence interval. (s): seconds. The right-most columns provide an inverse transformation of the coefficient estimates as a measure of seconds to contrast the standardized coefficients reported in the left-most columns.

Table C1 reports the results of our first exploratory analysis which excludes problem identifiers from the regression model and instead re-introduces an intercept. The pattern of results is consistent with those reported in Appendix B and in the manuscript. The findings suggest that explicitly accounting for problem-level identifiers in the model results in little-to-no impact on interpretation for this analysis.

Research Question 2: Effects of Sequencing

Table C2 reports the results of our second exploratory analysis aligned with our second research question. This analysis excludes problem pair identifiers from the regression and re-introduces an intercept to the model. In comparing these results to those of our primary analysis, we find that several differences emerge. Most notably, the incongruent-to-incongruent spacing sequence correlates with the fastest response times (as indicated by the positive coefficients for the other three sequence categories). Additionally, the incongruent-to-congruent spacing sequence exhibited the slowest response times, and was significantly slower than the other three spacing sequences. This finding aligns with our initial hypothesis that the response time would be the slowest when students transition from incongruent to congruent problems, but differs from the findings of our primary analysis addressing this research question.

Note: (CI): confidence interval. (s): seconds. The right-most columns provide an inverse transformation of the coefficient estimates as a measure of seconds to contrast the standardized coefficients reported in the left-most columns.