Abstract
Educational data mining has allowed for large improvements in educational outcomes and understanding of educational processes. However, there remains a constant tension between educational data mining advances and protecting student privacy while using educational datasets. Publicly available datasets have facilitated numerous research projects while striving to preserve student privacy via strict anonymization protocols (e.g., \(k\)-anonymity); however, little is known about the relationship between anonymization and utility of educational datasets for downstream educational data mining tasks, nor how anonymization processes might be improved for such tasks. We provide a framework for strictly anonymizing educational datasets with a focus on improving downstream performance in common tasks such as student outcome prediction. We evaluate our anonymization framework on five diverse educational datasets with machine learning-based downstream task examples to demonstrate both the effect of anonymization and our means to improve it. Our method improves downstream machine learning accuracy versus baseline data anonymization by 30.59%, on average, by guiding the anonymization process toward strategies that anonymize the least important information while leaving the most valuable information intact.Keywords
1. Introduction
Protecting student privacy is a central concern in educational data mining (Rubel and Jones, 2016). As described by Hutt et al., there is a conflict between two values: (i) the benefits that can come from educational data mining and (ii) the value of preventing harm, namely regarding privacy (Hutt et al., 2022). In the age of big data, methods to protect student privacy are not as straightforward as they once were. In 2018, Reidenberg and Schaub described the new ethical tensions that come from using big data for educational improvement while protecting privacy (Reidenberg and Schaub, 2018). Similarly, Pardo and Siemens provided principles for privacy in educational data mining by drawing from how other disciplines deal with privacy (Pardo and Siemens, 2014).
One point of tension involves how to keep student data safe. A common practice to uphold student privacy involves “de-identifying” student data. De-identifying student data means removing information that could link the data back to specific students. However, de-identifying student data is more nuanced than removing direct identifiers, such as names or email addresses (Yacobson et al., 2020). The removal of identifiers is important, but there are still re-identification risks associated with these data (Yacobson et al., 2020). Combinations of information only slightly related to identity can lead to high possibilities for re-identification (Yacobson et al., 2021). For example, Benitez and Malin describe that re-identification could come from an attacker matching de-identified lists of data to a dataset that is not de-identified and finding patterns that put the original de-identified data at risk (Benitez and Malin, 2010). Consequently, approaches like \(k\)-anonymity work towards protecting individuals in a dataset by ensuring that each individual is indistinguishable from at least \(k\) other individuals, given all of the information combined (Sweeney, 2002).
In addition to ethical requirements for preserving privacy, some jurisdictions have laws and privacy regulations that govern the collection, use, and sharing of personal data (e.g., the United States’ FERPA or the European Union’s GDPR (U.S. Department of Education, 1974, Council of the European Union, 2016)) (Khalil and Ebner, 2016). Anonymizing data also maintains trust between systems and students (Polonetsky and Jerome, 2014). \(k\)-anonymity is one tool to accomplish these privacy regulations. Some large student datasets that have previously been used for analysis in educational data mining harness \(k\)-anonymity (Kuzilek et al., 2017).
Because \(k\)-anonymity has widespread use, it has been the subject of research on methods to improve it for specific disciplines. For example, researchers proposed \(l\)-diversity as an extension of \(k\)-anonymity that provides further anonymity guarantees (Machanavajjhala et al., 2007). However, \(l\)-diversity is sometimes impossible to achieve for smaller datasets. In the medical field, there has been an improvement of \(k\)-anonymity for anonymizing specifically health datasets (El Emam et al., 2009). When it comes to improving privacy practices for educational data, research and decisions come from different perspectives. While a large amount of policy comes from government regulations such as FERPA and GDPR, Beardsley et al. address privacy issues from a student and teacher perspective—specifically to help students and teachers to better understand the risks of data sharing (Beardsley et al., 2019). Furthermore, researchers have designed data privacy models for computer-based learning (Ivanova et al., 2015). Since data sharing policy for education data comes from multiple fields, there is no generally agreed-upon practice. Following this, while options to ensure privacy do exist, they are not always adhered to (Kitto and Knight, 2019). Similarly, we are not aware of any policy for upholding privacy while also keeping educational data useful for various downstream tasks. We consider downstream tasks to be any data-driven component of an educational system. In our research, we focus on machine learning classification as one common type of downstream task.
While anonymization is a valuable step toward protecting student privacy, it has its drawbacks for prediction utility. In the medical field, researchers such as Lee et al. have been designing ways to preserve the downstream utility of datasets even after anonymization (Lee et al., 2017). Just as medical data are useful for doctors, educational data can be useful for teachers. For example, student data is useful in understanding learning by enabling the intelligent design of learning tools (Siemens, 2013).
1.1. Research objectives
This paper analyzes the effects of \(k\)-anonymity in educational data for use in subsequent educational data mining methods (i.e., machine learning models in this case), and proposes ideas to improve the anonymization process in certain educational scenarios. The aim is to improve student privacy while also preserving—as much as possible—machine learning prediction power on the anonymized datasets. We evaluate anonymization through experiments across five diverse educational datasets as described in section 3.
We address two research questions. The first considers the impact of anonymization on student data, and the second provides an algorithm to improve the existing method for student datasets.
Research Question 1: Is there a simple trade-off between the anonymization strength of \(k\)-anonymity
and downstream model accuracy?
We expect there to be a consistent trade-off between the level of anonymization and the utility of a
dataset on a downstream task. \(k\)-anonymity modifies data in two main ways: suppression (removing part
of each value, such as less significant digits) and generalization (collapsing or rounding related values
into higher levels of a hierarchical structure). These are both simple ways to manipulate data to reduce
detail. Since the detail—and thus information—of the data is reduced, we expect the usefulness of the
data to also decrease for downstream applications (i.e., machine learning in this case) that rely on the
data.
If there is a consistent trade-off between anonymization and performance, then it follows that weaker instances of anonymization will generally have higher downstream performance than stronger instances of anonymization. However, if there is not a consistent trade-off, possible instances of anonymization can be found that have higher downstream performance than less-anonymized instances, which implies that stricter anonymization is preserving more valuable information.
Research Question 2: Could anonymizing less important data more strictly improve downstream
machine learning classification performance?
We expect that preserving information in the most important features (i.e., a column of tabular data
used for prediction), at the expense of less important features, will improve the performance of
downstream tasks. Providing guidelines to an anonymization algorithm on the usefulness of features for
a downstream task should allow for the dataset to retain more relevant information about each data
point while still satisfying \(k\)-anonymity. If our hypothesis is correct, it has implications for
anonymization work in educational datasets. It implies that there is an area to further increase the
utility of their data for machine learning tasks while still preserving anonymity amongst the
data.
By deciphering if there is a consistent trade-off between anonymization and accuracy, we can further understand the effect anonymization might have on decreasing the value of the data in downstream educational data mining tasks. We propose a way to reduce the impact of anonymization on student data while still keeping it anonymous. Thus, the method anonymizes data for protecting students while also optimizing for future analysis tasks.
2. Background
As data become more and more widespread, the danger to a student’s privacy also increases. An individual’s data can never be perfectly secure (even state-of-the-art data protection systems are vulnerable to data breaches) (Cheng et al., 2017); however, many preventative measures have been developed to safeguard personal data privacy (Jain et al., 2016). Different tools have been created to help protect the privacy of individuals.
2.1. \(k\)-Anonymity
Latanya Sweeney created the \(k\)-anonymity model, upon which our proposed method is based, as a formal protection model to be deployed into real-world systems. The model focuses on protecting information wherein each data point cannot be distinguished from \(k\)-1 other data points (Sweeney, 2002). When a data point (row of data) represents a student, \(k\)-anonymity thus ensures that a student cannot be distinguished from their peers based on the dataset in question. The value \(k\) is chosen by the researcher or practitioner who is anonymizing the data. A large \(k\) results in increased data obfuscation, since more students are guaranteed to appear identical in terms of their data.
Scholars focused on medical data privacy developed the ARX data anonymization tool, which offers \(k\)-anonymity functionality (Prasser and Kohlmayer, 2015). Similarly, researchers and data security practitioners worked towards improving \(k\)-anonymity in regards to reducing over-anonymization in specific cases of health data (El Emam and Dankar, 2008). \(k\)-anonymity has also been improved for specialized tasks such as collaborative filtering for recommender systems (Wei et al., 2018). However, \(k\)-anonymity is only a small piece of the research for privacy preserving technologies. For example, in a recent survey on the use of anonymization in healthcare data, it was found that 75 different anonymization systems existed just in that subfield. Despite the large number of anonymization approaches, \(k\)-anonymity is still one of the most common given its simple yet powerful privacy guarantee (Sepas et al., 2022).
\(k\)-anonymity is also used to preserve student privacy in student data. For example, Buratović et al. used an extension of the \(k\)-anonymity algorithm with a focus on suppression to anonymize student data (Buratović et al., 2012, Samarati and Sweeney, 1998). A large student dataset, the Open University Learning Analytics Dataset (OULAD) used the ARX software program to \(k\)-anonymize their data with a \(k\) of 5 (Kuzilek et al., 2017), yielding an anonymous dataset that could be released publicly and has been cited over 300 times.
2.2. Student data anonymization
Despite the commonplace nature of both student data and processes for anonymizing data, there is no standardized method for how to properly de-identify and anonymize student data. Student data must be handled carefully since students are considered a vulnerable population; similar to medical records, student data also have high risks if not properly de-identified (Chicaiza et al., 2020). Several governments have tried to mitigate these risks by designing policies for handling student data. For example, the General Data Protection Regulation (GDPR) is a European policy to protect data (Council of the European Union, 2016). In the United States, the Family Educational Rights and Privacy Act (FERPA) is one of the main policies to protect student data (U.S. Department of Education, 1974). Alongside FERPA, many states have further laws to protect student privacy. In 1997, a technical brief put forward by the Institute of Education Sciences’ National Center for Education Statistics described how to properly protect student confidentiality when using student data (Cheung et al., 1997). They described methods of generalization and suppression—similar to the methods that \(k\)-anonymity provides.
While the use of student data holds its risks, the benefits from educational data mining are substantial. For example, Jia et al. recently showed the power of using the data-driven Insta-Reviewer for creating automatic feedback for student writing (Qinjin Jia et al., 2022). Researchers also harness video and image-based student data to predict reading comprehension, adding to the multitude of ways in which student data can improve learning (Caruso et al., 2022). Romero et al. summarize many other recent benefits of educational data mining as well (Romero and Ventura, 2020).
Considering the breadth of educational data mining research, some researchers have surveyed the field for common trends. For example, in 2020, Chicaiza et al. surveyed many educational data mining articles for mentions of their anonymization practices and found that fewer than 6% of the learning analytics papers had any mention of the privacy issue (Chicaiza et al., 2020). However, this does not mean that privacy is not integral to the field. At the Learning Analytics Conference in 2015, there was a workshop hosted about the ethical and privacy issues in learning analytics (Drachsler et al., 2015).
There are no well-established agreements on how researchers and practitioners ought to anonymize student data, apart from as required by law (U.S. Department of Education, 1974, Council of the European Union, 2016). However, even without an explicit agreement, researchers do understand the importance of implementing privacy protection into the pipeline. For example, Marshall et al. present a framework for integrating educational data mining and privacy-preserving technologies (Marshall et al., 2022). To further exemplify the impacts of privacy protection, in this paper, we study the effects of anonymization on downstream analyses using multiple datasets, as described next.
3. Methods
This section describes the algorithms and datasets used to display our results. We describe the
\(k\)-anonymity method in more detail and our improvement to that method for the educational data mining
domain. Our code to reproduce all analyses is hosted here:
https://github.com/fjstinar/improve-kanon-practices/.
3.1. Data
We performed analysis on five datasets that represent some common educational data mining situations to establish the generalizability of our results. We chose datasets with both diversity and reproducibility in mind. The first three datasets contain categorical and ordinal features, and the second two datasets consist of activity features. By using datasets of multiple feature types, we cover popular formats of tabular datasets in educational data mining.
3.1.1. Student Academics dataset
The Student Academics dataset contains 131 instances with 22 features. The data were collected from 3 colleges in India (Hussain et al., 2018). The features contain social, educational, and economic traits of students as well as time spent studying (a behavioral feature) and assessment grades (the outcome we predicted). Using demographic features as predictors is questionable, as described thoroughly by Baker et al. (Baker et al., 2023). However, as a means for analyzing the impact of anonymization and de-identification practices, these features of the dataset are still well worth considering given that they may be necessary for various downstream tasks apart from prediction, such as assessing the fairness of outcomes or predictive models (Baker and Hawn, 2022).
Data collected from students has varying levels of sensitive information, so it is important that the anonymization methods we use can be successfully applied to these more sensitive datasets. This dataset focuses on predicting end of the semester grades from social, economic, and academic traits. Thus, over half of the features used could be considered sensitive for the student (e.g., the social and economic features used).
3.1.2. Student Portuguese Performance dataset
We also analyzed the Student Portuguese Performance dataset (Cortez and Silva, 2008). This dataset tracks student achievement in secondary education across two high schools in Portugal. The dataset has 649 instances each with 33 features. The dataset is used to predict the final grade in the Portuguese language subject. From a privacy point of view, the dataset contains four types of features: identifiers, quasi-identifiers, sensitive attributes, and non-sensitive attributes. Identifiers are features that specifically have information that can identify an individual. Quasi-identifiers are features that could potentially identify an individual but are not explicit. Sensitive features hold information that is related to a student’s demographics (e.g., age). Non-sensitive features contain all of the other features that would not fit into the three previous categories mentioned.
3.1.3. Student Math Performance dataset
Similar to the previous dataset, the Student Math Performance dataset (Cortez and Silva, 2008) was collected from students in Portugal and includes the same 33 features as the previous dataset, but for 395 students in math classes rather than Portuguese classes. Similarly, this dataset predicts end of the year math grades.
3.1.4. Educational Process Mining (EPM) dataset
We also analyzed the Educational Process Mining dataset (Vahdat et al., 2015). As opposed to the previous datasets, the EPM dataset consists of students’ activities over time across multiple sessions while using electronics in a laboratory setting. Specifically, there are 115 students in the dataset. Each student could have up to 99 log files that contain their activities during the session. The features we extracted from the activity data consist of tracking mouse clicks/movements, keystrokes, exercises completed, and other similar features. The features are converted to continuous values on a scale of \(0\) to \(9\). The outcome of this dataset is the grades that students get from each session which is on a scale of \(0\) to \(6\).
3.1.5. MATHia dataset
Our last dataset is a large dataset from the MATHia intelligent tutoring system for middle school and high school math (Jiang et al., 2024). The dataset consists of 165 features across 611 instances. MATHia uses machine learning models to predict content mastery and thereby tailor instruction for each student as they learn. Machine learning models are based on data collected from students’ interactions with the different parts of the MATHia software, including records of their successes on various math problems, hints accessed, and how many answer attempts were made (Jiang et al., 2024). Our specific use case predicts “gaming the system” behaviors (Baker et al., 2004) that are annotated by a human expert. Labels for gaming the system, and features extracted to predict those labels, were adapted from previous work on the dataset (Baker et al., 2004).
3.2. Anonymization and utility
Anonymization is the process of transforming data to reduce the disclosure risk of instances from the original data (Marques and Bernardino, 2020). As with \(k\)-anonymity, anonymization typically involves either perturbing data, reducing the detail of the data points, or deleting data. Doing so increases the difference from the original data, including differences in identifying information, which decreases the risk of disclosure from the original data. The trade-off between anonymization and information loss here is considered the statistical disclosure control problem (Domingo-Ferrer and Rebollo-Monedero, 2009). The goal of anonymization is to remove identifying information, but some non-identifying information might also get removed (because it is impossible to tell the difference between identifying and non-identifying information, even if there is one). Furthermore, analyses such as machine learning might rely on that removed identifying information, or even if not, might rely on some non-identifying information that was inadvertently removed.
\(k\)-anonymity uses suppression and generalization to obfuscate data. Suppression replaces certain values in data with a placeholder value, such as an asterisk. Suppression is most commonly used for large ordinal alphanumeric values (e.g., ZIP codes in the U.S. are roughly ordered east to west) by suppressing less significant digits from the right to truncate their values. In this case, both 11236 and 11875 with suppression of up to 3 digits would be converted to 11***. Suppression thus makes similar values indistinguishable from each other. On the other hand, generalization replaces categorical values with broader categories, which may also be rounded numbers or might be higher levels of a categorical taxonomy. Generalization changes specific values into ranges of values. For example, if a dataset has “age” as a feature, instead of a specific age, generalization might convert it into age ranges (e.g., 20 to 30). Through suppressing and generalizing features, multiple entries can become identical with an anonymized dataset. Thus, a \(k\)-anonymized dataset is a dataset where each individual is indistinguishable from at least \(k-1\) other entries.
We further illustrate the \(k\)-anonymization process using a toy educational data mining dataset in Table 1. The left table is the initial dataset before anonymization. Each entry in the dataset is unique. For example, if we were given a student’s grade, we could also determine their ZIP code and age from these data with 100% accuracy. Once \(k\)-anonymity is applied to the dataset (right table in Table 1 with a \(k\) value of 2), we find that each entry has at least one other entry that is identical. Through generalizing the ”Grade” column and suppressing the “ZIP Code” column by one digit, we have a dataset that protects the individuals’ privacy more than the baseline. For example, if we know that a student received a grade of 93, we would know that the student is represented by the first entry. However, in the \(k\)-anonymized dataset, given the same information, we could only state that the student is either the first entry or the last entry. Thus, the dataset on the right side of Table 1 presents a distorted version of the original dataset obtained through the \(k\)-anonymization process. We show a \(k\)-anonymization of \(k=2\) in Table 1 rather than \(k=1\) because a dataset with a \(k=1\) is no different than an unanonymized dataset.
| Grade | ZIP Code | Age | Grade | ZIP Code | Age | |
|---|---|---|---|---|---|---|
| 93 | 80630 | 12 | x \(\ge \)90 | 8063* | 12 | |
| 72 | 80631 | 13 | x\(<\)90 | 8063* | 13 | |
| 78 | 80631 | 13 | x\(<\)90 | 8063* | 13 | |
| 96 | 80632 | 12 | x \(\ge \)90 | 8063* | 12 |
Changes in data due to anonymization further impact downstream tasks that use the distorted data. Particularly, the data become less useful for some downstream tasks. For example, if we use a dataset and its anonymized counterpart both as training data for two separate machine learning models, the model that was trained using the anonymized data could have lower scores on some evaluation metric such as AUC (area under the receiver operating characteristic curve) or variance explained. This is because anonymization transforms data through perturbing data, reducing detail, or entirely removing parts of a dataset. In the next section (RQ1), we further explore the effects of anonymization in an educational data mining context.
3.2.1. RQ1 method
To examine the anonymization versus performance trade-off (RQ1), we processed the Student Academics Dataset through a \(k\)-anonymization pipeline and an example downstream machine learning classification task. We chose the Student Academics Dataset for two reasons. The first is that the data contain both sensitive and non-sensitive features, which is representative of common real-world educational datasets. The second is that the dataset has a smaller complexity (22 categorical features) which allows us to confidently examine the intricacies of the \(k\)-anonymity process.
We performed \(k\)-anonymization using the ARX data anonymization tool (Prasser and Kohlmayer, 2015). ARX provides various tools for transforming data to adhere to privacy guidelines such as data anonymization and statistical disclosure control. ARX requires a schema for how to generalize values (i.e., which values or ranges of values should be grouped together at each level of increasing anonymization). In this case, we provided a simple generalization-style anonymization rule of grouping values in powers of 2 for our datasets. For example, given the values of \([1, 2, 3, 4, 5, 6]\), our rule would generalize the values to bins of form \([1 \) – \( 2, 3 \) – \( 4, 5 \) – \( 6]\) at one level of generalization. At a second level of generalization, the bins would be of form \([1 \) – \( 4, 5 \) – \( 6]\). ARX could thus explore ways to achieve \(k\)-anonymity by reducing the number of unique values of different features by a factor of 2 as many times as needed. We then enforced \(k\)-anonymity on the data for values of \(k\) from 1 (i.e., no anonymization) to 15. We then used each of these datasets as an input into a random forest classifier, trained via 3-fold student-independent cross-validation as an example of a classification problem that could likely follow from anonymized data. We trained the model 10 times with different random seeds and calculated AUC to measure accuracy. The results can be seen in Figure 1. While it is clear that there was some trade-off, there was not a consistent trend of decreasing downstream data utility as we predicted for RQ1.
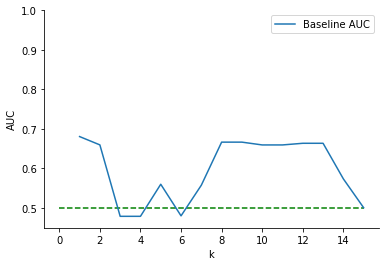
Initially, these results did not seem to follow from the utility and anonymity trade-off we described at the beginning of Section 3.2. Furthermore, Chicaiza et al. also found a case where downstream utility increased alongside an increase in anonymization from a MOOC dataset (Chicaiza et al., 2020). Hence, we further examined the process of the \(k\)-anonymity algorithm in this particular case as an illustrative example. \(k\)-anonymity exists when no data point in a dataset is able to be distinguished from at least \(k\) other data points. Thus, if we have a \(k\) = 3, any one data point will be indistinguishable from at least 3 other data points in the same dataset. As we increase \(k\), more information needs to be removed to ensure \(k\)-anonymity holds. This means that more data must be impacted; however, the same features in a dataset might not be changed as were changed for a smaller \(k\). For example, if we have the feature space {A,B,C}, \(k\)-anonymity with \(k\) = 2 might change features A and B. On the other hand, \(k\)-anonymity with a \(k\) = 3 might only change feature C instead. This is exactly what the ARX implementation of \(k\)-anonymity does (Prasser and Kohlmayer, 2015).
We examined the \(k\)-anonymized data corresponding to cases where AUC increased despite a higher value of \(k\) in Figure 1. We found that different features were indeed being anonymized at varied values of \(k\). One increase in AUC happened between \(k\) values 6 and 7. For \(k\) = 6, the non-suppressed features were 3 of the 4 parental-occupation-based features and the feature that describes friendships. Conversely, for \(k=7\), the non-suppressed features were a different subset of 3 of the 4 possible parental-occupation-based features, and whether or not school instruction was in English. That English instruction feature was particularly valuable for prediction, and so \(k\) = 6 had less utility for the downstream prediction task than \(k\) = 7 data. The \(k\)-anonymization algorithm is not “greedy” with respect to \(k\)—i.e., \(k\)-anonymized data are not necessarily a more anonymized version of \((k-1)\)-anonymized data—rather, it finds a unique distorted dataset that satisfies the given \(k\) value.
While these results did not align with our hypothesis, they do imply that there still are further ways to improve \(k\)-anonymity, specifically for student data where the eventual intended purpose is an educational data mining application such as predictive modeling of student outcomes. For example, in Figure 1 the best choice of \(k>1\) for data anonymization is at \(k=8\). A straightforward process for determining the best \(k\) does not exist: \(k=8\) was the best here because it had the highest downstream model performance while still maintaining a high level of data obfuscation. However, \(k=8\) was only known to be best because there was a downstream task that we could evaluate on. For researchers and educators who are anonymizing their own data that they collected for others to use, it is not clear how to find a value of \(k\) that satisfies both high data utility and high data anonymization. Thus, we propose our multi-step anonymization method that optimizes for both data utility and proper anonymization.
3.3. \(k\)-anonymity augmentation
As discussed, researchers in varying fields have developed methods towards improving \(k\)-anonymity for downstream tasks (El Emam and Dankar, 2008, Wei et al., 2018, Buratović et al., 2012). In the following section, we provide the first \(k\)-anonymity augmentation specifically made for predictive educational data mining tasks on student data, for common scenarios where there is a data provider (e.g., university/school data warehouse) that can perform basic analyses (e.g., simple linear associations) before sharing the anonymized data.
Since the fluctuations in performance caused by anonymization are in part due to which features are anonymized, a clear strategy for improvement is to assess which features are likely to be useful for downstream tasks and prioritize anonymization of the less-useful features when possible. We used a simple linear association heuristic to determine which features are likely to be useful. This heuristic is simple enough to be part of the anonymization process while maximizing generalizability to downstream tasks that explore more complex associations, by emphasizing “bias” in the bias–variance trade-off (Hastie et al., 2001).
3.3.1. RQ2 algorithm
Our algorithm adjusts the \(k\)-anonymization process by individually anonymizing features, enforcing more anonymization (even greater than \(k\)) for features less associated with a student outcome of interest, and finally recombining the individually anonymized features into a dataset and applying \(k\)-anonymity once more to ensure anonymity across all features. Since we re-anonymize the whole dataset as the last step, the privacy guarantees of \(k\)-anonymity still holds.
Step one of our method, as with a typical \(k\)-anonymity process, involves choosing some \(k\) to anonymize the data. We do not give any insight on how to choose this minimum value since it is a judgment that must be made based on the privacy requirements for the educational context in which data are collected; however, the decision can be informed by expert knowledge, disciplinary norms, legal requirements, or expertise regarding the dataset used.
We took two main strategies to preserve the most valuable information during anonymization. First, we estimated the “budget” of \(f\) features that could be kept at least partly un-anonymized by counting the number of features that still had variance left (i.e., not completely anonymized) after the dataset was initially \(k\)-anonymized. We then selected the \(f\) features with the strongest linear association to student outcome and discarded the rest. Specifically, in our case, we calculated the permutation importance of each feature in a linear model (Altmann et al., 2010). Next, we individually anonymized each of the \(f\) features with a scaled \(k\) according to the feature importance, where the most important feature was \(k\)-anonymized and subsequent features were anonymized with \(k_i = {\lfloor }k \times m \times c_i\rfloor \) where \(k_i\) is the \(k\) to use for the current feature \(i\), \(m\) is the maximum feature importance, and \(c_i\) is the feature importance for current feature \(i\). We used this scaled \(k_i\) only if the feature importance of all \(f\) features was less than 10% of the total feature importance, an indicator that the anonymization process had removed most of the important features. This means that less important features got much more of their information removed. Finally, after anonymizing each feature, we re-anonymized the combined set of individually anonymized columns with the current \(k\). To further illustrate our method, we provide a diagram of our algorithm in Figure 2.
To examine the impact of our method, we began by choosing an initial \(k\) to anonymize our datasets. Our experiments tested the impact of our method on data utility by examining downstream machine learning model performance. We anonymized our datasets from \(k\) = 1 (i.e., no anonymization) to \(k\) = 15 for a baseline \(k\)-anonymization method and our proposed method. Then, we processed the anonymized data through downstream machine learning models to examine the impacts on a typical classification model AUC.
4. Results
Here we present the results from our evaluation of the proposed algorithm for customized \(k\)-anonymity. We first outline our experimental setup used to conduct the analysis. We used all previously described datasets to evaluate our algorithm (described in 3.1). We evaluated downstream utility via AUC on both a random forest and a logistic regression classification model. We used two different models to represent differing possible downstream tasks. We evaluated both classification models via 10 iterations of training and testing with different random seeds and 3-fold student-independent cross-validation. Our complete results can be found in the appendix in table A1.
4.1. Student Academics dataset
We define our baseline performance model as outlined in section 3.2.1—i.e., with no customization for the \(k\)-anonymity process. We tested our algorithm against this \(k\)-anonymity baseline.
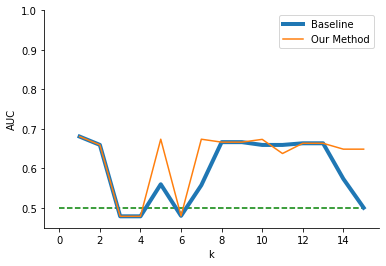
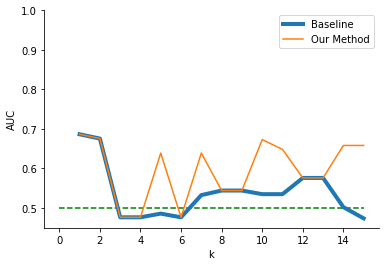
Figure 3 compares baseline \(k\)-anonymity to our method. Notably, our method yielded more accurate machine learning predictions across multiple values of \(k\). Both methods exhibited similar declines in performances for higher values of \(k\); however, our method was substantially better for certain \(k\) values. Specifically, at \(k=5\) the baseline method had an AUC of \(.560\) while our method had an AUC of \(.674\). While the baseline was slightly better for one value of \(k\) (i.e., 11), our proposed method was generally at least as good or better than the baseline for the random forest downstream task (average AUC = .626 versus .596 for the baseline).
Since different machine learning algorithms learn different types of patterns in the data (i.e., simple linear relationships versus nonlinear relationships with interactions between variables), we further tested our method with logistic regression as the downstream task. Without comparing methods, we first observed again that there was not a consistent trade-off between the strength of anonymization and downstream machine learning accuracy as our findings from RQ1 suggest. When comparing the baseline logistic regression and anonymization trade-off of Figure 3 to the trade-off seen when using our algorithm, we observed large fluctuations in downstream accuracy. We observed this with the baseline \(k\)-anonymization method at \(k=7\) with a sudden increase in accuracy. Figure 3 also displays that our method yielded improved downstream logistic regression accuracy for multiple values of \(k\) (average AUC = .597 versus .539 for the baseline).
4.2. Student Portuguese Performance dataset
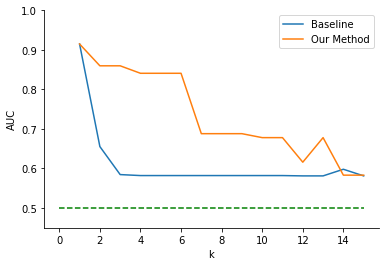
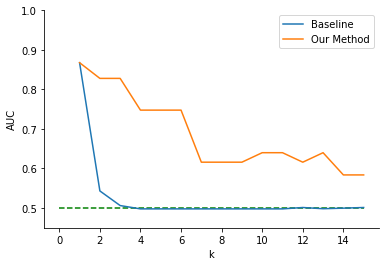
Figure 4 displays the average AUC on the random forest and logistic regression downstream tasks while increasing the value of \(k\) in the \(k\)-anonymization pipeline. Unlike our first analysis on the Student Academics Dataset, results here indicated a substantial decline in downstream performance related to an increase in anonymization. Even though we did not observe the same fluctuating downstream utility, our method still improved downstream data utility given its higher AUC for most values of \(k\). Our anonymization algorithm yielded equal or higher downstream accuracy across all values of \(k\) except for \(k=13\) on the random forest downstream task (average AUC = .736 versus .610 for the baseline). This dataset also illustrates clearly one of the largest hurdles with \(k\)-anonymity, which occurs when datasets have only a few important features for a given downstream task. Here, the baseline method removed all information from the most useful features even at small values of \(k\), yielding anonymized data with little utility for student outcome prediction.
For both logistic regression and random forest, our algorithm had better downstream accuracy for almost all \(k\) values tested. Figure 4 also displays the impacts of our anonymization algorithm on the logistic regression downstream performance. We found that our method yielded anonymized data sets with higher downstream utility for each value of \(k\) (average AUC = .687 versus .526 for the baseline) in logistic regression.
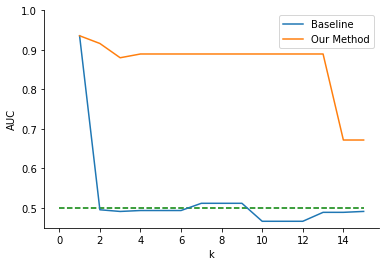
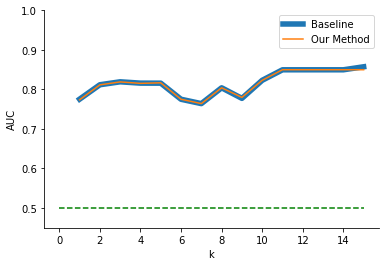
4.3. Student Math Performance dataset
Figure 5 displays a similar but more drastic trend versus the initial anonymization trade-off for the Student Portuguese Performance dataset shown in Figure 4. Our method yielded AUC \(\approx 0.88\), until higher values of \(k\) at around \(k=13\), whereas the baseline method removed all usable prediction information from the dataset for any level of anonymization (i.e., \(k > 1\)). Thus, our method returned a higher AUC for all tested values of \(k\) (average AUC = .864 versus .520 for the baseline).
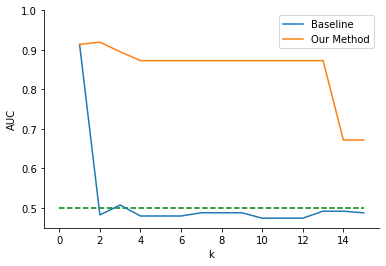
We further analyzed our algorithm’s impact when a logistic regression was used as the downstream task rather than the random forest. When logistic regression is chosen as the downstream task, we found a similar trade-off between performance and increasing the levels of anonymization as the Student Portuguese Performance Dataset. Figure 5 represents our baseline AUC versus anonymization trade-off and the impacts of our algorithm on the trade-off. In this case, our method also produced datasets that had consistently higher downstream model accuracy than the baseline (average AUC = .853 versus .513 for the baseline).
4.4. Educational Process Mining dataset
When analyzing the EPM dataset, we saw trends similar to those in the previous datasets. Figure 6 displays the results of our method compared to the baseline \(k\)-anonymity algorithm across the random forest and logistic regression algorithms, as in the previous results. For the random forest, our method yielded AUC \(\approx 0.76\) across all values of \(k\). The baseline method quickly fell from the initial AUC and plateaued at AUC \(\approx 0.56\). Thus, for the EPM dataset, our method produced datasets that yielded consistently higher model accuracy than baseline \(k\)-anonymity for the given downstream task (average AUC = .765 versus .588 for the baseline).
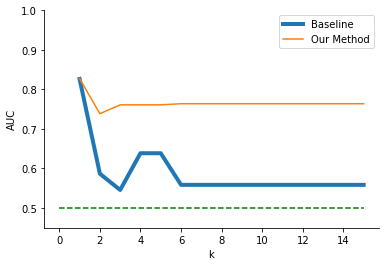
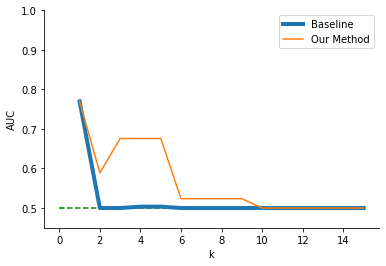
When we used the logistic regression downstream task, we again found that our method led to consistently better or equal accuracy versus the baseline method. The baseline method removed all useful downstream prediction information for any level of anonymization once the prediction accuracy dropped to \(0.5\) after \(k\) began to increase. On the other hand, our method successfully preserved some information for downstream prediction through \(k = 9\). Therefore, for values of \(k\) less than 9, our method provided higher accuracy as opposed to baseline \(k\)-anonymity (average AUC = .565 versus .518 for the baseline).
Note that the EPM dataset consists of activity and log data of the students rather than categorical features as in the previously analyzed datasets. Despite the shift in the type of data, our method still consistently provided anonymized data that yielded higher accuracy for the given downstream tasks.
4.5. MATHia dataset
We also performed the same analysis using the MATHia dataset. This dataset was extracted from interaction log data that is used to predict whether or not a student is “gaming the system” (Baker et al., 2004). Figure 7 shows the baseline and our method’s results on the MATHia dataset with increasing levels of anonymization. Similar to our previous results involving other datasets, the accuracy and anonymization trade-off were not consistent. Despite there being stronger anonymization as \(k\) increases, the AUC from the random forest model did not strictly decrease and indeed increased. Additionally, our method had little to no effect versus the baseline. Investigation of these patterns revealed that the dataset has many useful, similar features. That is, there exist many features that hold similar information and are also predictive for the downstream classification task. Thus, the baseline method included useful information in the anonymized result even without any guidance toward which features were linearly associated with the outcome. Moreover, the dataset may have benefited slightly from reducing the feature space by essentially randomly deleting features (a consequence of anonymization), reducing over-fitting and improving accuracy. That is, the benefits could be from our method reducing dimensionality. Thus, our method yielded no benefits relative to baseline \(k\)-anonymity in this dataset, unlike the others.
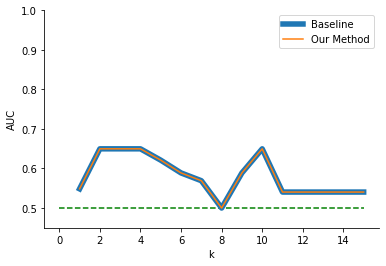
For logistic regression (Figure 7), we again observed no improvement or worsening from our method relative to the baseline. Both our method and the baseline also yielded variable downstream model AUC and, overall, much lower AUC than random forest. Logistic regression may not be an appropriate choice for this dataset, given that it does not work well even without anonymization (i.e., \(k\) = 1) and despite efforts to improve the model via \(L_2\) regularization (varied by powers of 10 from 0.001 to 100) and scaling input data by converting to \(z\)-scores, none of which were successful.
5. Discussion
Overall, our results strongly imply one main takeaway: the expected data utility and anonymization trade-off is not straightforward. We first see this from our results for RQ1, where stricter anonymization sometimes led to an increase in downstream machine learning model AUC. In our analyses, a \(k\) = 1 indicates no anonymization present, thus for all higher values of \(k\) the amount of machine learning performance degradation can be seen in Table A1. We found that across all 20 dataset and machine learning model combinations, 16 combinations had a level of increased anonymization that gave a higher downstream AUC as opposed to lower levels of anonymization. Consequently, we presented an algorithm explored in RQ2 for customizing anonymization to improve utility for subsequent educational data mining prediction tasks.
For nearly all values of \(k\) in our analysis, we found a scaled anonymity processed dataset that had more or equal utility for the downstream task relative to the baseline. The only times our method failed to produce a data set with more or equal utility for the downstream task was for values of \(k > 10\). However, on average, our method produced higher downstream utility for all experiments except for the MATHia results (average 30.59% improvement across all experiments, including MATHia). We assume that the data anonymization step for most learning analytic tasks is an initial step that only happens once. Thus, finding a best case or even a better case than baseline anonymization has wide downstream benefits.
The MATHia analysis yielded two unique insights. The first is that our method did not supply a meaningfully worse dataset for downstream tasks than the baseline \(k\)-anonymization algorithm, even when the baseline was surprisingly good for downstream tasks. The second is that substantial complex patterns (e.g., nonlinear effects, interactions) were preserved even in the anonymized data, as evidenced by the difference between random forest and logistic regression in the downstream prediction task.
The results also show that there are still ways to improve the anonymization steps used for student data and educational datasets. We provide only one method for increasing the utility of student data while still upholding privacy measures. We proposed systematically scaling anonymization for the top features for classification and anonymizing data in iterations. Finally, we then anonymize the dataset completely once more so that the \(k\)-anonymity guarantees are upheld. By doing this, we ensure that the most impactful features for the downstream task are left with the least amount of anonymization, thus improving the conditional utility of the dataset that is processed. However, some results still show substantial increases in AUC after stricter anonymization (e.g., at \(k\) = 5 in Figure 3), which indicates that there must also be a better \(k\) = 4 solution, which could perhaps be found with a better heuristic.
Our proposed method allows for generalizability with respect to some of the specific steps used. \(k\)-anonymity is only one algorithm for anonymizing datasets. Random forests and logistic regressions are only two modeling strategies, and AUC is only one measure of accuracy. Our methods and framework allow for switching the modeling method and the evaluation metrics while still maintaining the optimization strategy presented. Moreover, the choice of the linear association heuristic was particularly chosen for the downstream task of classification via machine learning. However, the heuristics used could be replaced with different functions if needed for a different type of downstream task, though it was not necessary for the improved machine learning model performance seen in the results.
The problem that our method addresses arises because of one particular aspect of \(k\)-anonymity: \(k\)-anonymity is not necessarily related to \((k - 1)\)-anonymity or \((k + 1)\)-anonymity. Thus, \(k\)-anonymity has the ability to preserve or redact entirely different features for a different level of \(k\). We observed this in section 3.2.1. At \(k=6\), out of features {A,B,C,D,E,F}, {A,B,C,E} were suppressed. On the other hand at \(k=7\), {A,B,D,F} were suppressed. Notably, at \(k=7\), features that were suppressed in \(k=6\) were no longer suppressed. Thus, it was possible for downstream accuracy to improve, and for data utility to increase despite stricter data anonymization.
While other research has noted that performance does not strictly decline when the level of anonymization is increased (Chicaiza et al., 2020), our results provided a robust analysis of these findings. By focusing on understanding the intricacies of \(k\)-anonymity, we were able to further improve the datasets it generated for diverse educational data mining classification tasks.
5.1. Limitations
We observed two main limitations to our research. The first is that our approach of focusing on anonymization to uphold student privacy is insufficient in itself. We do not assume that the technological approach to privacy is enough to guarantee student privacy, especially given that datasets do not exist in isolation but come from students who may be represented in many other data sources (e.g., social media) that could be linked together. Anonymization is thus only one part of upholding student privacy. Student privacy must be protected from multiple different angles (Prinsloo et al., 2022). Other options could entail differential privacy which adds noise to data to preserve the privacy of individuals (Friedman and Schuster, 2010, Dankar and Emam, 2013) or even making pledges towards not selling student data in the future (Zeide, 2017). Possible future work would be to create ways in which researchers could combine multiple ways of protecting student privacy.
The second limitation is that we focused on a few specific types of educational data, including categorical, ordinal, and continuous data. However, educational data mining research sometimes concerns other unique types of data (e.g., images, essays) that may require substantially different approaches if they cannot be represented effectively in a tabular form. Thus, while our method is useful for tabular data, it lacks generalizability to data of different modalities due to the fact that it operates on high-level features encoded as columns in a dataset, whereas datasets suitable for applications such as deep learning may have very high-dimensional, low-level data that are not suitable to \(k\)-anonymity nor our modified approach. Future work is needed to explore methods for analyzing these data with educational data mining goals in mind.
6. Conclusion
As anonymization methods become more sophisticated, our understanding of the benefits and limitations of these methods also grows. For example, optimal \(k\)-anonymity is an NP-hard problem (Basu et al., 2015). Thus, we only have heuristic approaches such as ours to guide results for particular purposes such as educational data mining. As users and collectors of student data, we ought to improve our methods as the field changes, including making sure that the data we have are as useful as possible while still upholding student privacy. In educational data mining, we are limited to the data we can use. Thus, it is critical that we use our data such that it has the highest utility while still maintaining the privacy of the students. The method described in this paper is one such way, which we have shown can lead to datasets that are more useful for downstream prediction tasks.
For educational data mining researchers, we recommend using our method for student data anonymization when the downstream task is known. If the downstream task is ambiguous, our method would not be any worse than regular \(k\)-anonymity on average. We hope that these methods are the beginning of reimagining anonymization techniques for the educational data mining space.
7. Acknowledgments
This research was supported by NSF grant no. 2000638. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
8. Editorial Statement
Nigel Bosch had no involvement with the journal’s handling of this article in order to avoid a conflict with his Accessibility Production Editor role. The entire review process was managed by the Editor Agathe Merceron and Special Guest Editors Jaclyn Ocumpaugh and Maria Mercedes T. Rodrigo.
References
- Altmann, A., Toloşi, L., Sander, O., and Lengauer, T. 2010. Permutation importance: A corrected feature importance measure. Bioinformatics 26, 10 (Apr.), 1340–1347. DOI: https://doi.org/10.1093/bioinformatics/btq134.
- Baker, R. S., Corbett, A. T., Koedinger, K. R., and Wagner, A. Z. 2004. Off-task behavior in the cognitive tutor classroom: When students “game the system”. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. CHI ’04. Association for Computing Machinery, New York, NY, USA, 383–390. DOI: https://doi.org/10.1145/985692.985741.
- Baker, R. S., Esbenshade, L., Vitale, J., and Karumbaiah, S. 2023. Using demographic data as predictor variables: A questionable choice. Journal of Educational Data Mining 15, 2 (Jun.), 22–52. DOI: https://doi.org/10.5281/zenodo.7702628.
- Baker, R. S. and Hawn, A. 2022. Algorithmic bias in education. International Journal of Artificial Intelligence in Education 32, 1052–1092. DOI: https://doi.org/10.1007/s40593-021-00285-9.
- Basu, A., Nakamura, T., Hidano, S., and Kiyomoto, S. 2015. k-anonymity: Risks and the reality. In 2015 IEEE Trustcom/BigDataSE/ISPA. IEEE, Helsinki, Finland, 983–989. DOI: https://doi.org/10.1109/Trustcom.2015.473.
- Beardsley, M., Santos, P., Hernández-Leo, D., and Michos, K. 2019. Ethics in educational technology research: Informing participants on data sharing risks. British Journal of Educational Technology 50, 3, 1019–1034. DOI: https://doi.org/10.1111/bjet.12781.
- Benitez, K. and Malin, B. 2010. Evaluating re-identification risks with respect to the HIPAA privacy rule. Journal of the American Medical Informatics Association 17, 2 (Mar.), 169–177. DOI: https://doi.org/10.1136/jamia.2009.000026.
- Buratović, I., Miličević, M., and Žubrinić, K. 2012. Effects of data anonymization on the data mining results. In 2012 Proceedings of the 35th International Convention MIPRO. IEEE, Piscataway, NJ, 1619–1623.
- Caruso, M., Peacock, C., Southwell, R., Zhou, G., and D’Mello, S. 2022. Going deep and far: Gaze-based models predict multiple depths of comprehension during and one week following reading. In Proceedings of the 15th International Conference on Educational Data Mining, A. Mitrovic and N. Bosch, Eds. International Educational Data Mining Society, Durham, United Kingdom, 145–157. DOI: https://doi.org/10.5281/ZENODO.6852998.
- Cheng, L., Liu, F., and Yao, D. D. 2017. Enterprise data breach: Causes, challenges, prevention, and future directions: Enterprise data breach. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 7, 5 (Sept.), 1–14. DOI: https://doi.org/10.1002/widm.1211.
- Cheung, O. M., Clements, B. S., and Pechman, E. M. 1997. Protecting the Privacy of Student Records: Guidelines for Educational Agencies. U.S. Dept. of Education, Office of Educational Research and Improvement, Educational Resources Information Center, Washington, DC.
- Chicaiza, J., Cabrera-Loayza, M. C., Elizalde, R., and Piedra, N. 2020. Application of data anonymization in learning analytics. In Proceedings of the 3rd International Conference on Applications of Intelligent Systems, N. Petkov, N. Strisciuglio, and C. M. Travieso-González, Eds. APPIS 2020. Association for Computing Machinery, New York, NY, USA, 1–6. DOI: https://doi.org/10.1145/3378184.3378229.
- Cortez, P. and Silva, A. 2008. Using data mining to predict secondary school student performance. In Proceedings of 5th Annual Future Business Technology Conference, J. L. Afonso, C. Cuoto, A. Lago Ferreiro, J. S. Martins, and A. Nogueiras Melèndez, Eds. Vol. 5. EUROSIS-ETI, 5–12.
- Council of the European Union. 2016. General data protection regulation (GDPR) (l119, 4 may 2016, p. 1–88).
- Dankar, F. K. and Emam, K. E. 2013. Practicing differential privacy in health care: A review. Trans. Data Priv. 6, 35–67.
- Domingo-Ferrer, J. and Rebollo-Monedero, D. 2009. Measuring risk and utility of anonymized data using information theory. In Proceedings of the 2009 EDBT/ICDT Workshops. ACM, Saint-Petersburg Russia, 126–130. DOI: https://doi.org/10.1145/1698790.1698811.
- Drachsler, H., Hoel, T., Scheffel, M., Kismihók, G., Berg, A., Ferguson, R., Chen, W., Cooper, A., and Manderveld, J. 2015. Ethical and privacy issues in the application of learning analytics. In Proceedings of the Fifth International Conference on Learning Analytics And Knowledge. ACM, Poughkeepsie New York, 390–391. DOI: https://doi.org/10.1145/2723576.2723642.
- El Emam, K. and Dankar, F. K. 2008. Protecting privacy using k-anonymity. Journal of the American Medical Informatics Association 15, 5 (Sept.), 627–637. DOI: https://doi.org/10.1197/jamia.M2716.
- El Emam, K., Dankar, F. K., Issa, R., Jonker, E., Amyot, D., Cogo, E., Corriveau, J.-P., Walker, M., Chowdhury, S., Vaillancourt, R., Roffey, T., and Bottomley, J. 2009. A globally optimal k-anonymity method for the de-identification of health data. Journal of the American Medical Informatics Association 16, 5 (09), 670–682. DOI: https://doi.org/10.1197/jamia.M3144.
- Friedman, A. and Schuster, A. 2010. Data mining with differential privacy. In Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, Washington DC USA, 493–502. DOI: https://doi.org/10.1145/1835804.1835868.
- Hastie, T., Tibshirani, R., and Friedman, J. 2001. The elements of statistical learning. Springer series in statistics, 2 ed. Springer, Heidelberg, New York.
- Hussain, S., Abdulaziz Dahan, N., Ba-Alwi, F. M., and Ribata, N. 2018. Educational data mining and analysis of students’ academic performance using WEKA. Indonesian Journal of Electrical Engineering and Computer Science 9, 2 (Feb.), 447–459. DOI: https://doi.org/10.11591/ijeecs.v9.i2.pp447-459.
- Hutt, S., Baker, R. S., Ashenafi, M. M., Andres-Bray, J. M., and Brooks, C. 2022. Controlled outputs, full data: A privacy-protecting infrastructure for MOOC data. British Journal of Educational Technology 53, 4 (July), 756–775. DOI: https://doi.org/10.1111/bjet.13231.
- Ivanova, M., Grosseck, G., and Holotescu, C. 2015. Researching data privacy models in eLearning. In 2015 International Conference on Information Technology Based Higher Education and Training (ITHET). IEEE, Lisbon, Portugal, 1–6. DOI: https://doi.org/10.1109/ITHET.2015.7218033.
- Jain, P., Gyanchandani, M., and Khare, N. 2016. Big data privacy: A technological perspective and review. Journal of Big Data 3, 1 (Dec.), 25:1–25. DOI: https://doi.org/10.1186/s40537-016-0059-y.
- Jiang, L., Belitz, C., and Bosch, N. 2024. Synthetic dataset generation for fairer unfairness research. In LAK ’24: Proceedings of the 14th Learning Analytics and Knowledge Conference. Association for Computing Machinery, 200–209. DOI: https://doi.org/10.1145/3636555.3636868.
- Khalil, M. and Ebner, M. 2016. De-identification in learning analytics. Journal of Learning Analytics 3, 1 (Apr.), 129–138. DOI: https://doi.org/10.18608/jla.2016.31.8.
- Kitto, K. and Knight, S. 2019. Practical ethics for building learning analytics. British Journal of Educational Technology 50, 6, 2855–2870. DOI: https://doi.org/10.1111/bjet.12868.
- Kuzilek, J., Hlosta, M., and Zdrahal, Z. 2017. Open University Learning Analytics dataset. Scientific Data 4, 1 (Nov.), 170171. DOI: https://doi.org/10.1038/sdata.2017.171.
- Lee, H., Kim, S., Kim, J. W., and Chung, Y. D. 2017. Utility-preserving anonymization for health data publishing. BMC Medical Informatics and Decision Making 17, 1 (Dec.), 104. DOI: https://doi.org/10.1186/s12911-017-0499-0.
- Machanavajjhala, A., Kifer, D., Gehrke, J., and Venkitasubramaniam, M. 2007. L-diversity: Privacy beyond k-anonymity. ACM Trans. Knowl. Discov. Data 1, 1 (Mar.), 3–es. DOI: https://doi.org/10.1145/1217299.1217302.
- Marques, J. F. and Bernardino, J. 2020. Analysis of data anonymization techniques. In International Conference on Knowledge Engineering and Ontology Development. KEOD, SciTePress, Setubal, Portugal, 235–241. DOI: https://doi.org/10.5220/0010142302350241.
- Marshall, R., Pardo, A., Smith, D., and Watson, T. 2022. Implementing next generation privacy and ethics research in education technology. D. Ladjal, S. Joksimovic, T. Rakotoarivelo, and C. Zhan, Eds. British Journal of Educational Technology 53, 4, 737–755. DOI: https://doi.org/10.1111/bjet.13224.
- Pardo, A. and Siemens, G. 2014. Ethical and privacy principles for learning analytics. British Journal of Educational Technology 45, 3, 438–450. DOI: https://doi.org/10.1111/bjet.12152.
- Polonetsky, J. and Jerome, J. 2014. Student Data: Trust, Transparency, and the Role of Consent. Vol. 1. Future of Privacy Forum, Washington DC. DOI: https://doi.org/10.2139/ssrn.2628877.
- Prasser, F. and Kohlmayer, F. 2015. Putting statistical disclosure control into practice: The ARX data anonymization tool. In Medical Data Privacy Handbook, A. Gkoulalas-Divanis and G. Loukides, Eds. Springer International Publishing, Cham, 111–148. DOI: https://doi.org/10.1007/978-3-319-23633-9_6.
- Prinsloo, P., Slade, S., and Khalil, M. 2022. The answer is (not only) technological: Considering student data privacy in learning analytics. British Journal of Educational Technology 53, 4, 876–893. DOI: https://doi.org/10.1111/bjet.13216.
- Qinjin Jia, Young, M., Yunkai Xiao, Jialin Cui, Chengyuan Liu, Rashid, P., and Gehringer, E. 2022. Insta-reviewer: A data-driven approach for generating instant feedback on students’ project reports. In Proceedings of the 15th International Conference on Educational Data Mining, A. Mitrovic and N. Bosch, Eds. International Educational Data Mining Society, Durham, United Kingdom, 5–16. DOI: https://doi.org/10.5281/ZENODO.6853099.
- Reidenberg, J. R. and Schaub, F. 2018. Achieving big data privacy in education. Theory and Research in Education 16, 3 (Nov.), 263–279. DOI: https://doi.org/10.1177/1477878518805308.
- Romero, C. and Ventura, S. 2020. Educational data mining and learning analytics: An updated survey. WIREs Data Mining and Knowledge Discovery 10, 3, e1355. DOI: https://doi.org/10.1002/widm.1355.
- Rubel, A. and Jones, K. M. L. 2016. Student privacy in learning analytics: An information ethics perspective. The Information Society 32, 2, 143–159. DOI: https://doi.org/10.1080/01972243.2016.1130502.
- Samarati, P. and Sweeney, L. 1998. Generalizing data to provide anonymity when disclosing information. In Proceedings of the Seventeenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems. PODS ’98. Association for Computing Machinery, New York, NY, USA, 188. DOI: https://doi.org/10.1145/275487.275508.
- Sepas, A., Bangash, A. H., Alraoui, O., El Emam, K., and El-Hussuna, A. 2022. Algorithms to anonymize structured medical and healthcare data: A systematic review. Frontiers in Bioinformatics 2, 984807. DOI: https://doi.org/10.3389/fbinf.2022.984807.
- Siemens, G. 2013. Learning analytics: The emergence of a discipline. American Behavioral Scientist 57, 10, 1380–1400. DOI: https://doi.org/10.1177/0002764213498851.
- Sweeney, L. 2002. k-anonymity: A model for protecting privacy. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 10, 05, 557–570. DOI: https://doi.org/10.1142/S0218488502001648.
- U.S. Department of Education. 1974. Family educational rights and privacy act (FERPA) (20 U.S.C. § 1232g; 34 CFR part 99).
- Vahdat, M., Oneto, L., Anguita, D., Funk, M., and Rauterberg, M. 2015. Educational Process Mining (EPM): A learning analytics data set. UCI Machine Learning Repository. DOI: https://doi.org/10.24432/C5NP5K.
- Wei, R., Tian, H., and Shen, H. 2018. Improving k-anonymity based privacy preservation for collaborative filtering. Computers & Electrical Engineering 67, 509–519. DOI: https://doi.org/10.1016/j.compeleceng.2018.02.017.
- Yacobson, E., Fuhrman, O., Hershkovitz, S., and Alexandron, G. 2020. De-identification is not enough to guarantee student privacy: De-anonymizing personal information from basic logs. In Companion Proceedings 10th International Conference on Learning Analytics and Knowledge (LAK20), V. Kovanović, M. Scheffel, N. Pinkwart, and K. Verbert, Eds. 149–151.
- Yacobson, E., Fuhrman, O., Hershkovitz, S., and Alexandron, G. 2021. De-identification is insufficient to protect student privacy, or – what can a field trip reveal? Journal of Learning Analytics 8, 2 (Sept.), 83–92. DOI: https://doi.org/10.18608/jla.2021.7353.
- Zeide, E. 2017. Unpacking student privacy. In Handbook of Learning Analytics, First ed., C. Lang, G. Siemens, A. Wise, and D. Gasevic, Eds. Society for Learning Analytics Research (SoLAR), New York, New York, 327–335. DOI: https://doi.org/10.18608/hla17.028.
A. Appendix: Detailed results
| Acad. | Por. | Math | EPM | MATHia | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RF | LR | RF | LR | RF | LR | RF | LR | RF | LR
| |||||||||||
| B | M | B | M | B | M | B | M | B | M | B | M | B | M | B | M | B | M | B | M | |
| \(k\) = 1 | .681 | .681 | .687 | .687 | .915 | .915 | .868 | .868 | .936 | .936 | .914 | .914 | .827 | .827 | .769 | .769 | .775 | .775 | .549 | .549 |
| \(k\) = 2 | .659 | .659 | .676 | .676 | .655 | .859 | .543 | .828 | .496 | .916 | .483 | .917 | .587 | .739 | .500 | .589 | .812 | .812 | .649 | .649 |
| 3 | .479 | .479 | .477 | .477 | .585 | .859 | .506 | .828 | .491 | .880 | .508 | .895 | .546 | .761 | .500 | .676 | .819 | .819 | .649 | .649 |
| 4 | .479 | .479 | .477 | .477 | .582 | .841 | .498 | .748 | .494 | .889 | .479 | .873 | .639 | .761 | .503 | .676 | .816 | .815 | .649 | .649 |
| 5 | .560 | .674 | .486 | .639 | .582 | .841 | .498 | .748 | .494 | .889 | .479 | .873 | .639 | .761 | .503 | .676 | .816 | .816 | .621 | .621 |
| 6 | .480 | .480 | .476 | .476 | .582 | .841 | .498 | .748 | .494 | .889 | .479 | .873 | .559 | .764 | .500 | .524 | .775 | .775 | .589 | .588 |
| 7 | .558 | .674 | .533 | .639 | .582 | .688 | .498 | .616 | .512 | .889 | .488 | .873 | .559 | .764 | .500 | .524 | .764 | .764 | .569 | .569 |
| 8 | .667 | .667 | .544 | .544 | .582 | .688 | .498 | .616 | .512 | .889 | .488 | .873 | .559 | .764 | .500 | .524 | .804 | .804 | .500 | .500 |
| 9 | .667 | .667 | .544 | .544 | .582 | .688 | .498 | .616 | .512 | .889 | .488 | .873 | .559 | .764 | .500 | .524 | .777 | .779 | .589 | .589 |
| 10 | .659 | .674 | .535 | .637 | .582 | .678 | .498 | .639 | .466 | .889 | .474 | .873 | .559 | .764 | .500 | .500 | .823 | .823 | .649 | .649 |
| 11 | .659 | .637 | .535 | .648 | .582 | .678 | .498 | .639 | .466 | .889 | .474 | .873 | .559 | .764 | .500 | .500 | .849 | .849 | .540 | .540 |
| 12 | .664 | .664 | .576 | .576 | .581 | .616 | .501 | .616 | .466 | .889 | .474 | .873 | .559 | .764 | .500 | .500 | .849 | .849 | .540 | .540 |
| 13 | .664 | .664 | .576 | .576 | .581 | .678 | .498 | .639 | .489 | .889 | .492 | .873 | .559 | .764 | .500 | .500 | .849 | .849 | .540 | .540 |
| 14 | .574 | .649 | .502 | .658 | .598 | .583 | .499 | .584 | .489 | .672 | .492 | .672 | .559 | .764 | .500 | .500 | .849 | .849 | .540 | .540 |
| 15 | .501 | .649 | .474 | .658 | .581 | .583 | .501 | .584 | .491 | .672 | .488 | .672 | .559 | .764 | .500 | .500 | .857 | .849 | .540 | .540 |