Abstract
Bayesian Knowledge Tracing (BKT) is a well-established model for formative assessment, with optimization typically using expectation maximization, conjugate gradient descent, or brute force search. However, one of the flaws of existing optimization techniques for BKT models is convergence to undesirable local minima that negatively impact performance and interpretability of the BKT parameters (i.e., parameter degeneracy). Recently, deep knowledge tracing methods such as context-aware attentive knowledge tracing have proven to be state-of-the-art in performance; however, these methods often lack the inherent interpretability or understanding provided by BKT’s skill-level parameter estimates and student-level mastery probability estimates.We propose a novel optimization technique for BKT models using a neural network-based parameter generation approach, OptimNN, that leverages hypernetworks and stochastic gradient descent for training BKT parameters. We extend this approach and propose BKTransformer, a transformer-based sequence modeling technique that generates temporally-evolving BKT parameters for student response correctness prediction. With both approaches, we demonstrate improved performance compared to BKT and deep KT baselines, with minimal hyperparameter tuning. Importantly, we demonstrate that these techniques, despite their state-of-the-art expressive capability, retain the interpretability of skill-level BKT parameter estimates and student-level estimates of mastery and correctness probabilities.
Our code and data can be found at https://github.com/abadrinath947/OptimNN.
Keywords
1. Introduction
Knowledge tracing (KT) is a well-researched approach to estimating students’ cognitive mastery in the context of computer tutoring systems based on problem response sequences (Pelánek, 2017). Tutoring systems take a problem-solving or active approach to learning (Aleven and Koedinger, 2002, Anzai and Simon, 1979) that often resembles the personalized mastery learning approach researched by Bloom (1984).
Bayesian Knowledge Tracing (BKT) (Corbett and Anderson, 1994) can be described as a Hidden Markov Model that models per-skill binary student knowledge and correctness states using four trainable parameters. It has served as a reliable approach to knowledge tracing and is used in deployed computerized tutoring systems (Ritter et al., 2007).
However, one of the issues with BKT is its tendency to converge to local minima across different optimization techniques, such as expectation maximization (EM) and conjugate gradient descent (CGD) (Yudelson et al., 2013). Besides reduced performance on correctness prediction, many of these local minima result in degenerate BKT parameters (Baker et al., 2008, van de Sande, 2013). While techniques such as Dirichlet priors or rules about allowable ranges of parameters have been suggested, they are either not effective in preventing parameter degeneracy by themselves (Baker et al., 2008) or not scalable to large datasets and different variants of BKT. Work by Pardos and Heffernan (2010) suggests that altering the EM initialization such that it did not contain degenerate parameters could lead to non-degenerate fitted parameters. While this sometimes reduces the number of degenerate parameters, it is not consistently effective and the margin of improvement over randomly initialized EM is not significant (Table 4).
In recent years, deep learning has been used to improve upon the accuracy of knowledge tracing with models such as Deep Knowledge Tracing (DKT) (Piech et al., 2015), DKT+ (Yeung and Yeung, 2018), and Self-Attentive Knowledge Tracing (SAKT) (Pandey and Karypis, 2019). Though they present a higher performance in correctness prediction, these methods lose access to directly interpretable probabilistic skill-level estimates (e.g., learn rate) and estimation of the student mastery probability. While approaches such as clustering or dimensionality reduction can be used for explainability as in Pandey and Karypis (2019), we believe that they are indirect and often subjective techniques for interpreting these methods.
Techniques such as Deep-IRT and Deep Learning-Based Knowledge Tracing (DLKT) have been developed and used for explainable deep KT (Yeung, 2019, Lu et al., 2020). Deep-IRT provides performance on-par with DKT, and it presents explainability in terms of scalar values indicating (a) student ability and (b) problem difficulty. However, we believe the explainable elements have unclear relevance without specific dataset and problem-specific context (i.e., it is unclear what a student ability of 0.3 implies without further context). DLKT leverages backpropagation techniques to interpret the predictions of the sequence modeling technique for KT. It is also limited in the explainable components it presents, using a “relevance” metric whose definition is more vague than a direct probabilistic interpretation attainable with BKT. None of these techniques present as much direct probabilistic interpretability about the skill and student-specific information as the BKT parameters and mastery probabilities.
We propose an optimization technique to bridge the gap between performance of deep KT methods and interpretability of BKT, using neural networks to generate BKT parameter values. Addressing concerns associated with local minima, degenerate parameters, and allowing for a deep KT extension, we summarize the highlights of our study as follows.
-
We demonstrate that our technique, OptimNN, generates superior local minima for BKT compared to other optimization techniques such as EM and stochastic gradient descent (SGD), while maintaining significantly lesser degenerate parameters.
-
We present an extension to the proposed technique, BKTransformer, combining deep KT methods with OptimNN to achieve a balance between the expressive nature of sequence learning via transformers and interpretability of BKT. Using this, we achieve performance rivalling or surpassing state-of-the-art KT methods such as SAKT.
-
Importantly, we show that both OptimNN and BKTransformer show insensitivity to hyperparameters and demonstrate interpretability at the same level as traditional BKT methods.
2. Related Work
2.1. Bayesian Knowledge Tracing
BKT has been serving as the canonical model for knowledge tracing and is typically modeled as a Hidden Markov Model (van de Sande, 2013). A standard BKT model consists of four learned parameters (prior \(P(L_0)\), learn \(P(T)\), guess \(P(G)\), and slip \(P(S)\) as shown in Equations 1-4) per skill. At time \(t\) of a problem solving sequence, the student mastery probability is given by \(P(L_t = 1)\), and the student correctness probability is given by \(P(\mathrm {obs}_t = 1)\).
\begin {align} P(L_0) &= P(L_1 = 1) \\ P(T) &= P(L_{t+1} = 1 \mid L_t = 0) \\ P(G) &= P(\mathrm {obs}_t = 1 \mid L_t = 0) \\ P(S) &= P(\mathrm {obs}_t = 0 \mid L_t = 1) \label {eqn:bkt} \end {align}
Many of the extensions to BKT have diversified the four parameters by modifying the modelling structure or incorporating information such as individualization per student (Yudelson et al., 2013) or making contextual estimations of the probability of guess and slip (Baker et al., 2008). Item Learning Effect (ILE) conditions or multiplexes the learn rate based on the item (Pardos and Heffernan, 2009), and Item Difficulty Effect (KT-IDEM) fits a different guess and slip rate per item (Pardos and Heffernan, 2011).
2.2. Optimization Techniques for BKT
Standard approaches to optimizing BKT parameters include expectation maximization (EM)
(Levinson et al., 1983), conjugate gradient descent (CGD) (Corbett and Anderson,
1994), or discretized brute force parameter search (Baker et al., 2008). Popular
implementations that use EM for optimization include BNT-SM (Chang et al.,
2006) and pyBKT(Badrinath et al., 2021). hmm-scalable implements
both EM and CGD, along with other optimization techniques (Yudelson, 2016). To our
knowledge, techniques popular in the deep learning regime such as stochastic gradient descent
(SGD) have been less popular than these techniques, perhaps due to the lack of theoretical
guarantees.
Discretized brute force parameter search presents the ability to easily discard regions in the search grid to achieve local minima without “degenerate” parameters (e.g., where guess is greater than 0.5) (Baker et al., 2008). However, one of the issues with this approach is lack of scalability as the time complexity grows exponentially with the number of trainable parameters (e.g., for extensions such as KT-IDEM, which may have hundreds or thousands of parameters). For EM, Pardos and Heffernan (2010) showed that initialization with non-degenerate parameters can lead to non-degenerate fitted parameters.
2.3. Deep Knowledge Tracing
Deep Knowledge Tracing (DKT) uses a recurrent neural network to predict correctness for problem solving sequences with the ability to model interdependence in skills unlike BKT, which assumes skill independence and the Markov property (Piech et al., 2015). DKT outperforms BKT and many proposed variants in terms of prediction accuracy across a wide range of datasets. Recent years have seen a boom in the development and application of DKT, such as incorporating problem-level features (Zhang et al., 2017) and side information (Wang et al., 2019).
Other work based on DKT, such as DKT+, has leveraged machine learning techniques such as regularization to improve performance (Yeung and Yeung, 2018). Self-Attentive Knowledge Tracing (SAKT) (Pandey and Karypis, 2019) introduced a transformer model based on self-attention for student performance prediction, showing improvements over methods such as DKT. (Ghosh et al., 2020) incorporate several improvements such as a context-aware relative distance measure, exponentially decaying attention weights, and usage of the Rasch model to regularize concept and question embeddings. Other techniques building upon deep KT have leveraged graph learning (Nakagawa et al., 2019, Tong et al., 2020), text-based featurization (Liu et al., 2019, Yin et al., 2019), and incorporated forgetting features (Abdelrahman and Wang, 2022, Nagatani et al., 2019).
2.4. Interpreting Deep KT Techniques
Deep KT techniques typically rely on different notions of interpretability compared to BKT as they do not produce explicit probabilistic estimations of a student’s learn, guess, slip, and prior for a particular skill. Typically, embeddings produced by deep KT techniques such as DKT and SAKT can be used alongside dimensionality reduction (e.g., T-SNE) to visualize and interpret the model and its outputs. Both Piech et al. (2015) and Pandey and Karypis (2019) include these types of analyses for DKT and SAKT respectively. However, while these reveal latent structure, they lack direct interpretability without the subjective application of techniques such as clustering.
Unlike DKT, Deep-IRT explicitly presents explainability for KT in terms of scalar values indicating student ability and problem difficulty (Yeung, 2019). However, without contextualizing these scalars in the context of the dataset and student cohort, they are difficult to interpret directly (e.g., in a probabilistic manner). DLKT leverages layer-wise relevance propagation to interpret deep KT techniques (Lu et al., 2020), using neural network backpropagation to inversely attribute the prediction made by the deep learning method back to the neural network layers (Bach et al., 2015). That said, it is similarly limited in the directly explainable components it presents, using a more vaguely-defined “relevance” metric. Labra and Santos (2023) leverage data augmentation for training explainable deep KT models by mixing ground-truth data with data generated by a “surrogate” explainable model. Similarly, the explainability of this approach is limited in practical use since it is measured by how well the surrogate replicates the predictions of the trained deep KT model.
Concretely, we believe that no existing deep learning-based KT technique presents as much probabilistic interpretability about the skill-specific information as the BKT parameters and about the student’s knowledge state as the generated mastery probabilities.
3. Optimization of Bayesian Knowledge Tracing with Parameter Generation
In this section, we motivate and outline the proposed optimization approach, OptimNN, that leverages a feed-forward neural network architecture and stochastic gradient descent (SGD). With regards to the generated parameters, we discuss the ability to add penalty terms to OptimNN’s loss function to discourage degenerate parameter values and specify prior distributions over BKT parameters (Baker et al., 2008, Rai et al., 2009).
3.1. Optimization using SGD
To motivate the benefits of the proposed neural network-based parameter generation approach, we outline a similar preliminary method to optimize BKT parameters using SGD without neural networks. This is shown in Algorithm 1, where we follow the instructions shown for SGD on Lines 17 and 20.
Note that we have simplified the fitting algorithm for brevity and ease of understanding in two ways. In the algorithm, we apply gradient steps for each student problem solving sequence, whereas we might use a batch in practise. Another practical consideration that is left out for brevity is that gradient updates could lead to impossible values of probabilistic parameters (e.g., prior \(>\) 1). To resolve this, we can (a) clip the values between 0 to 1 or (b) store the parameters as logits and use the sigmoid function to transform the logit into a probability. In our case, we choose option (b) to retain as much gradient flow as possible.
3.1.1. Forward Pass
The forward computation as shown in \(\textsc {forward}\) in Algorithm 1 is reminiscent of a standard BKT
implementation, such as pyBKT(Badrinath et al., 2021), with the BKT parameters
being initialized randomly for each skill \(s_i\) (Line 17, SGD). Using the generated correctness
probabilities \(P(\mathrm {obs}_{s_i, t} = 1)\) across problem solving sequences, we compute the loss with respect to the
observed correctness using the binary cross-entropy loss (Line 12), as shown in Equation
\eqref{eqn:bce}.
\begin {align} \mathrm {BCELoss}(\mathrm {obs}, P(\mathrm {obs})) &= \sum _{t=1}^{|\tau |} \mathrm {obs}_{t} \log P(\mathrm {obs}_{t} = 1)\nonumber \\ &+ (1 - \mathrm {obs}_{t}) \log (1 - P(\mathrm {obs}_{t} = 1)) \label {eqn:bce} \end {align}
3.1.2. Optimization
The backward pass is powered by the automatic differentiation (“autodiff”) package provided by deep learning libraries (Paszke et al., 2019, Chollet et al., 2015). In this case, autodiff would return the gradient with respect to the trainable BKT parameters \(\mathbf {\theta }_{s_i} = [P(L_0)_{s_i}, P(T)_{s_i}, P(G)_{s_i}, P(S)_{s_i}]\) (Line 20, SGD). To optimize the parameters, we take a gradient step based on the data with learning rate \(\alpha \) (not to be confused with BKT’s learn rate \(P(T)\)).
3.1.3. Benefits and Drawbacks
While Algorithm 1 is similar in some ways to other gradient-based approaches, there are several advantages to using SGD with a standard deep learning package such as PyTorch. The autodiff package allows for optimization without manual gradient computation during the backward pass (i.e., the parameter update phase) (Paszke et al., 2019). This increases the flexibility and ease-of-use in adapting the algorithm, for example, to support additional BKT variants.
However, this preliminary approach still has some drawbacks, including the necessity to tune the learning rate \(\alpha \) size depending on the dataset. As an example, we use this approach to train on the ASSISTments 2009-10 Skill Builder dataset using different learning rates. Figure 6 (right) demonstrates that this approach is quite sensitive to the learning rate and that a learning rate of 0.01 is roughly optimal for this dataset, which is quite different from the default of 0.0001 or 0.001 in deep learning libraries (Paszke et al., 2019, Chollet et al., 2015). This tuning would likely need to performed for every dataset to determine learning rates for fast convergence and optimal performance.
3.2. Neural Network Parameter Generation
To alleviate the concerns expressed in Section 3.1 about tuning for effective usage of SGD, we leverage feedforward neural networks. Instead of randomly initializing BKT parameters and iteratively optimizing them through SGD, we can construct a “parameter generation network” \(f_\phi : \mathbb N \mapsto (0, 1)^4\) that generates or computes the 4 BKT parameters given a particular skill; that is, \(\theta _{s_i} = f_\phi (s_i)\) instead of being randomly initialized by 4 numbers and trained. We refer to this approach as OptimNN, shown in Figure 1.
In the backward pass, instead of optimizing \(\theta _{s_i}\) directly, we optimize the parameter generation network \(f_\phi \) using the gradient \(\frac {\partial L}{\partial \phi }\) (Line 20, OptimNN) such that the generated parameters \(\theta _{s_i} = f_\phi (s_i)\) are more appropriate in computing accurate correctness probabilities \(P(\mathrm {obs})\).
3.2.1. Forward Computation
The forward computation of correctness and mastery probabilities of a student sequence uses the same forward algorithm as described in Algorithm 1. The main difference is that the BKT parameters \(\theta _{s_i}\) are generated by a neural network \(f_\phi : \mathbb N \mapsto (0, 1)^4\), rather than being initialized randomly. This change is reflected in Line 17 (OptimNN) of the algorithm. Note that this neural network does not take student sequences of observed correctness as input; it only takes a skill ID \(s_i \in \mathbb N\), as shown in Figure 1.
This change can be viewed as an equivalent re-expression of the BKT optimization problem, and it is similar to hypernetworks (Ha et al., 2017) or black-box adaptation meta learning (Santoro et al., 2016). Instead of learning a table of parameters using an iterative algorithm like SGD, we employ neural network-based functional approximation to learn an optimal mapping from the skill to its optimal BKT parameters. Although this might seem unnecessarily complex, we show in Sections 3.2.3 and 6 that this method has several advantages, including improved numerical stability, vastly reduced hyperparameter tuning, increased flexibility in preventing parameter degeneracy, and empirical performance improvements over SGD and existing optimization methods.
3.2.2. Optimization
As the BKT parameters are generated by a neural network \(f_\phi \), parameterized by trainable neural network parameters \(\phi \), we compute the gradient of the loss function with respect to \(\phi \) instead to optimize the network \(f_\phi \) (Line 20, OptimNN). That is, since \(\theta _{s_i} = f_\phi (s_i)\) are generated, they are not trainable parameters for the purposes of this method (they are effectively “intermediate computations”). Note that there is an important distinction between the neural network parameters \(\phi \) that parameterize \(f_\phi \), and the BKT parameters, which are outputted by \(f_\phi \) (\(\theta _{s_i} = f_\phi (s_i)\)).
By updating \(\phi \) using gradient descent to minimize the loss function, we iteratively update the parameter generation network \(f_\phi \) to be able to generate more appropriate BKT parameters, such that the \(\textsc {forward}\) update produces more accurate correctness probabilities with respect to the observed values.
3.2.3. Benefits and Drawbacks
Compared to optimization using SGD (i.e., without neural networks), this method does not suffer from the same hyperparameter tuning and convergence issues. Although this may seem counterintuitive since we still use gradient descent, neural network optimizers such as Adam tend to require minimal tuning to achieve competitive local minima for deeper neural networks (Kingma and Ba, 2015). Empirically, we find that the default learning rate of 0.001 performs consistently well across datasets unlike SGD without a neural network, as demonstrated in Section 6 and Figure 6. Further, this optimization method can be adapted easily to any BKT variant that multiplexes parameters (e.g., guess rate) per item or student by adding an additional feature to the input of a neural network (i.e., \((s_i, k_i)\), for some item-related feature \(k_i\)) for the prediction of that BKT parameter.
3.3. Regularization for Generated Parameters
We present an extension of the framework outlined in Section 3.2 that supports preferences and rules to discourage undesirable or degenerate parameter values. To judge our approach, which we call OptimNN-Reg, we adopt guidelines based on the work in Baker et al. (2008) and van de Sande (2013) to construct the following rules shown for allowable and non-degenerate parameters: \begin {align} P(S)_{s_i} &< 0.5 \label {eqn:6} \\ P(G)_{s_i} &< 0.5 \\ P(T)_{s_i} &< \frac {1 - P(S)_{s_i}}{P(G)_{s_i}} \label {eqn:learndeg} \end {align}
Additionally, OptimNN-Reg provides support for establishing a prior over one or more BKT parameters across one or more skills using any differentiable distribution. For example, we choose a Dirichlet distribution \(\mathrm {[guess, 1 - guess]} \sim \mathbf {Dir}([6, 14])\) to establish a prior about the guess rate across across all skills (Rai et al., 2009). Note that as described in Rai et al. (2009), a variety of approaches can be used to select this Dirichlet prior, including domain knowledge and automatic approaches.
We implement these rules and preferences as regularizing terms (or penalties) added to the binary cross-entropy loss function with a chosen coefficient \(\lambda _i\). The higher the value of \(\lambda _i\), the greater the effect on the loss function and the more aggressively that rule or preference will be encouraged. While another valid approach to satisfy the rules would be to simply restrict the values of the slip and guess probabilities via a transformation which outputs real numbers between the range of 0 to 0.5 (e.g., applying a sigmoid operation divided by two), it is less flexible than our regularization or penalty-based approach. Our penalty-based approach not only effectively generalizes to simple bound-based rules, but it could be used in more complex distribution-based rules (as in Equation \eqref{eqn:reg}, for instance). Since the constraint in our approach is also not “hard”, it is also possible to specify constraints which are optional and can be violated in favour of maximizing the primary objective of correctness prediction.
All the inequalities shown in Equations \eqref{eqn:6}-\eqref{eqn:learndeg} are modeled using the \(\max \) function and the prior is applied by maximizing the log probability of the generated parameters under the distribution. The resulting minimization objective to optimize \(\phi \), the neural network parameters for \(f_\phi \), for skill \(s_i\) is shown in Equation \eqref{eqn:reg}.
\begin {align} \arg \min _\phi \mathrm {BCELoss}(\phi ) &+ \lambda _1 \max (P(S)_{s_i} - 0.5, 0) \nonumber \\ &+ \lambda _2 \max (P(G)_{s_i} - 0.5, 0) \nonumber \\ &+ \lambda _3\max (P(T)_{s_i} - \frac {1 - P(S)_{s_i}}{P(G)_{s_i}}, 0) \nonumber \\ &- \lambda _4 \log P(\mathrm {guess} = P(G)_{s_i}) \label {eqn:reg} \end {align}
Note that the above objective can be adapted easily with any combination of rules and preferences, i.e., using a Dirichlet prior with another parameter, specifying \(P_\phi (T) < 0.9\), etc.
4. Extending OptimNN using Sequence Modeling
While OptimNN presents a framework to generate non-degenerate BKT parameters, it is still limited by the global optima within the set of all BKT models. With the advent of deep KT models that demonstrate superior performance to BKT models, we present an extension of OptimNN, BKTransformer, leveraging transformer-based sequence modeling. Retaining many desirable properties of OptimNN such as its interpretability, BKTransformer allows for improved generalization and more expressive capabilities through deep learning.
4.1. Motivating Example
To motivate an extension of a parameter generation approach using sequence modeling, consider a simple example in which a student incorrectly answers a series of \(t\) questions for a particular skill \(s_i\). Suppose we have access to arbitrary non-degenerate, learned BKT parameters \(P(G) < 0.5, P(S) < 0.5\). Additionally, we are even able to assume any reasonable probability of forgetting, \(P(F) = P(L_{t+1} = 0 \mid L_t = 1) < 1 - P(T)\), where this “forgets” extension is used by Khajah et al. (2016).
From an intuitive perspective, we would expect a probability of knowledge that decays corresponding to incorrect responses, with the eventual expectation of having a near-zero \(P(L_t)\) as \(t \to \infty \). This corresponds to the intuition that without a singular correct response, it would seem unreasonable for there to exist a non-zero probability of correctness or mastery. However, given the standard BKT forward pass as shown in Algorithm 1 with a fixed set of BKT parameters and the above assumptions, we show that the eventual probability of mastery \(P(L_\infty )\) converges to greater than the learned value of \(P(T)\). In fact, the mastery probability \(P(L_t) > P(T)\) for all \(t\). The complete derivation of the posterior probability, next latent state, and limit is presented in Appendix A.
Example 4.1. For any set of non-degenerate learned BKT parameters, i.e., \(P(G) < 0.5, P(S) < 0.5\) with \(P(F) < 1 - P(T)\), and any timestep \(t \in [1, \infty )\)
\begin {align*} P(L_t) &= (1 - P(F)) P(L_{t-1} \mid \mathrm {obs}_{t-1}) + P(T) (1 - P(L_{t-1} \mid \mathrm {obs}_{t-1}))\\ &> P(T) \end {align*}
Importantly, regardless of the learned prior rate \(P(L_0)\), the mastery probability \(P(L_t)\) for this example scenario is at least \(P(T)\) for the given parameters, even as \(t \to \infty \) (i.e., greater than the learn rate, despite incorrectly answering all questions). When the learned “learn rate” \(P(T)\) is large and potentially degenerate (i.e., violating Equation \eqref{eqn:learndeg}), this is not a desirable outcome since the corresponding correctness prediction is likely a high likelihood of correctness despite unboundedly many incorrect answers (for all time).
To practically and empirically validate this simple scenario in the context of actual learned BKT parameters, we examine learn rates from BKT trained on the CognitiveTutor Bridge to Algebra 2008-09 dataset. For instance, consider the case of the skill “find sphere volume in context,” with a learn rate of 0.887, in the 85th percentile of learn rates. Under this scenario (i.e., even by answering all questions incorrectly), the student’s mastery probability converges to \(P(L_\infty ) \to 1\) and eventual correctness probability of 0.886, which is unreasonable. Not only does the estimate indicate perfect certainty of mastery despite answering all questions incorrectly, but the produced estimates of the correctness probability always incorrectly classifies the true correctness for all \(t\).
4.2. Temporal Extension of BKT Parameters
To motivate a temporal extension to the BKT that allows for changing parameters over time, we draw inspiration from sequence modeling techniques, such as long-short term memory networks (Hochreiter and Schmidhuber, 1997) or transformers (Vaswani et al., 2017), which retain an evolving hidden state \(z_t\) over timesteps. Conditioned on this hidden state, these methods produce a prediction \(y_t\). Similarly, to extend the expressiveness of our modeling framework and to allow for performance competitive with sequence modeling methods such as DKT, we consider BKT parameters that vary as a function of time \(t\) that are used to produce a correctness prediction.
By default, the standard BKT parameters do not vary based on the time \(t\), i.e., all the parameter values at any arbitrary time within the problem solving sequence \(t_0\) and \(t_1 \ne t_0\) are equal (e.g., \(\text {slip}[t_0] = \text {slip}[t_1]\), \(\text {learn}[t_0] = \text {learn}[t_1]\), and so on). To achieve BKT parameters that vary over timesteps, we propose that for any time step \(t\), the standard BKT parameter set can be extended as \(\text {learn}[t] = P(T)_t, \text {guess}[t] = P(G)_t, \text {slip}[t] = P(S)_t\). Note that the prior cannot vary as a function of the time since it is a parameter representing the initial probability of mastery.
\begin {align} P(L_0) &= P(L_1 = 1) \\ P(T)_t &= P(L_{t+1} = 1 \mid L_t = 0) \label {eqn:timestep1} \\ P(G)_t &= P(\mathrm {obs}_t = 1 \mid L_t = 0) \\ P(S)_t &= P(\mathrm {obs}_t = 0 \mid L_t = 1) \label {eqn:timestep} \end {align}
This temporally conditioned parameter extension to BKT can be modeled using existing extensions to BKT by multiplexing the respective parameters based on the time within the problem solving sequence. However, there are several drawbacks to the method, which may reduce its performance and interpretability. As with all other BKT models, the (time-specific) parameters are static. That is, for all students attempting a skill at time \(t\), the relevant BKT parameters are the same regardless of the student or prior sequence. A possible way to fix this is to multiplex based on time and student (or item), but this would require sufficient data in each time step and student/item. The second limitation is that the number of parameters grows as a function of the maximum number of time steps, which can result in poor efficiency if there exist long training sequences. Finally, this multiplexed set of BKT parameters can be prone to degenerate parameters as previously, and the parameter values can vary by arbitrary amounts across consecutive and nearby timesteps.
4.3. Parameter Generation using Transformer Models
To generate optimal values for temporally-evolving BKT parameters that address the issues highlighted in the previous section, we leverage an expressive sequence modeling approach conditioned on the student’s problem sequence. Following successful techniques in deep KT, such as SAKT (Pandey and Karypis, 2019), we leverage a transformer decoder architecture with masked multi-head attention, based on the GPT-2 architecture. While our transformer architecture resembles SAKT, the primary point of difference between SAKT’s architecture and the architecture of our proposed method is the final fully-connected prediction layer, which outputs BKT parameters as opposed to the correctness prediction.
To that end, we extend the framework presented in Section 3 and propose a parameter generation network \(h_{\phi ,\psi }(\mathbf {obs}_{1..t}, \mathbf {s}_{1..t+1}): \mathbb N^t \times \mathbb N^{t + 1} \mapsto (0, 1)^3\) that generates or computes the BKT parameters in Equations \eqref{eqn:timestep1}-\eqref{eqn:timestep} at time \(t + 1\) given a problem sequence of length \(t\) and the skill attempted at timestep \(t + 1\). To explicitly construct this parameter generation network, we leverage the previously defined base parameter network \(f_\phi \), which generates BKT parameters for a given skill without conditioning on the student sequence or timestep, and a “parameter adjustment” transformer decoder \(g_\psi \), which additively adjusts the BKT parameters generated by \(f_\phi \). The parameter adjustment transformer \(g_\psi \) is designed to adjust the base parameters generated by \(f_\phi \) to effectively adapt the parameters to the specific student sequence. Formally, we construct the temporally-evolving parameter generation network \(h_{\phi ,\psi }\), as shown in Equation \eqref{eqn:transformereqn}.
\begin {align} h_{\phi ,\psi }^t(\mathbf {obs}_{1..t}, \mathbf {s}_{1..t+1}) = f_\phi (s_{t+1})_{2..4} + g_{\psi }(\mathbf {obs}_{1..t}, \mathbf {s}_{1..t}) \label {eqn:transformereqn} \end {align}
While this construction allows for adaptive parameter generation as desired, the parameter adjustments can vary arbitrarily over time. To address this, we develop a set of penalties to ensure that the BKT parameters do not change arbitrarily over time (i.e., we constrain the parameter adjustment network to output small and consistent values). Precisely, we augment the objective shown in Equation \eqref{eqn:reg} with the following terms for parameter adjustments being penalized by a coefficient \(\lambda _5\) and differences in parameter adjustments over consecutive timesteps being penalized by a coefficient \(\lambda _6\). Ignoring the prior over guess probabilities (i.e., \(\lambda _4 = 0\)), the resulting objective is shown in Equation \eqref{eqn:reg2}. Note that since \(h_{\phi , \psi }\) is composed of a sum of two differentiable components, we are able to apply the same gradient descent-based technique described in Section 3 to optimize the parameters \(\phi \) and \(\psi \).
\begin {align} \arg \min _{\phi , \psi } \mathrm {BCELoss}(\phi , \psi ) &+ \lambda _1 \max (P(S)_{t,s_i} - 0.5, 0) \nonumber \\ &+ \lambda _2 \max (P(G)_{t,s_i} - 0.5, 0) \nonumber \\ &+ \lambda _3\max (P(T)_{t,s_i} - \frac {1 - P(S)_{t,s_i}}{P(G)_{t,s_i}}, 0) \nonumber \\ &+ \lambda _5 ||g_{\psi }(\mathbf {obs}_{1..t}, \mathbf {s}_{1..t+1})||_2 \nonumber \\ &+ \lambda _6 ||g_{\psi }(\mathbf {obs}_{2..t}, \mathbf {s}_{2..t+1}) - g_{\psi }(\mathbf {obs}_{1..t-1}, \mathbf {s}_{1..t})||_2 \label {eqn:reg2} \end {align}
Finally, to capture the expressive capability of methods like DKT, we do not separate the sequences for a student based on the skill (i.e., as for BKT) as input to the parameter adjustment network \(g_\psi \). Instead, for a student, we maintain a mastery probability \(P(L_t)_{s_i}\) for all skills \(s_i\) in a vector \(\mathbf {P(L_t)}\) rather than for a singular skill individually. At each timestep \(t-1\) in the sequence, we update the corresponding element \(\mathbf {P(L_t)}_{s_t}\) based on \(s_t\) using the BKT forward pass and the generated parameters from \(h_{\phi , \psi }\). We refer to this technique as BKTransformer, and its architecture is depicted visually in Figure 2.
Importantly, this approach addresses all the areas of concern expressed in the previous section. It allows for adaptive parameter generation conditioned on the current sequence, and it does not incur significantly higher parameterization for arbitrarily long sequences. Combined with the penalty terms listed in the objective in Equation \eqref{eqn:reg2}, we are able to avoid degenerate parameters as well.
This recurrent parameter modeling framework differs from DKT and other deep learning techniques for knowledge tracing (Piech et al., 2015). Instead of directly predicting the probability of correctness, we predict BKT parameters, which can in turn allow for prediction of correctness and mastery. This allows us to analyze and interpret the way in which correctness predictions are made through skill-level parameters, whereas for methods such as DKT, the direct (probabilistic) way in which the correctness predictions are constructed are blackboxed behind uninterpretable neural network computations. This framework allows access to the latent mastery state through the predicted mastery probability. While this does not allow for full interpretability of the method (i.e., there are still perhaps millions of neural network computations), our approach’s correctness predictions can be probabilistically justified by the produced slip, guess, forget, and learn parameters, which provide a layer of interpretability and structure over the deep learning component.
5. Experimental Setup
5.1. Datasets
We use the ASSISTments 2009-10/2012-13 Skill Builder ( AST09/ AST12), Cognitive Tutor KDD Cup Algebra 2008-09 Challenge ( ALG08) and Bridge to Algebra ( BRI08) datasets. We summarize the properties of each raw dataset in Table 1. The datasets provide variety in terms of size in responses and number of skills and students, and they contain item-level information, which allows for evaluation of fitting models such as KT-IDEM and ILE (Pardos and Heffernan, 2009, Pardos and Heffernan, 2011).
To pre-process the datasets, we remove all rows with no skill attached. For any rows with multiple skills attached, we treat each unique set of skills as its own skill. When training any model with item-level parameters, we impute missing or unseen item information (e.g., problem template ID) for a particular row of data with the most common item in the training set.
5.2. Evaluation Methodology
To evaluate OptimNN, we compare its performance across the chosen datasets. For evaluation of BKT and its variants using OptimNN, we compare to other optimization techniques in the literature: EM, SGD, and CGD. Across each of these techniques, the variants of BKT we choose for evaluation include: BKT, KT-IDEM (Pardos and Heffernan, 2011), and ILE (Pardos and Heffernan, 2009). We believe this presents a well-rounded evaluation across a variety of datasets, optimization techniques, and BKT variants. Note that due to lack of existing implementations for CGD on KT-IDEM and ILE, we only evaluate CGD on BKT.
We implement SGD in PyTorch by following Algorithm 1, with the only differences in our
implementation being the practical considerations mentioned in Section 3.1. We implement OptimNN
in PyTorch, using a 3-layer neural network with a hidden size of 128. We use a learning rate of 0.01 for
SGD and 0.001 (default) for OptimNN. For the EM implementation, we use pyBKT(Badrinath
et al., 2021) and choose the best model fit after 5 random initializations. For the
CGD implementation, we use hmm-scalable(Yudelson, 2016), with the Hestenes-Stiefel
formula (Hestenes and Stiefel, 1952). All models are trained until a plateau in the training
loss.
We implement BKTransformer in PyTorch, leveraging a transformer decoder architecture for \(g_\psi \) based on minGPT, with 2 transformer layers, a hidden size of 128, and 4 transformer heads. As before, the network \(f_\phi \) is implemented using PyTorch as a 3-layer neural network with a hidden size of 128.
To evaluate BKTransformer, we compare to deep KT techniques on the four chosen datasets, with BKT-EM as a baseline. For deep KT techniques, we compare to DKT and SAKT, which represent contemporary methods from recent years. All deep learning methods are trained with a learning rate of 0.0005 using the AdamW optimizer (Kingma and Ba, 2015) in PyTorch. For all experiments, we use root-mean squared error (RMSE) as the evaluation metric, using the corrected resampled t-test method to generate confidence intervals (Gardner and Brooks, 2017).
5.3. Fitted Parameter Evaluation
To evaluate the BKT parameter quality produced by OptimNN with regularization (OptimNN-Reg) and BKTransformer (i.e., Equation \eqref{eqn:reg}), we use Equations \eqref{eqn:6}-\eqref{eqn:learndeg} to determine the percent of rule-violating parameter values (RVP) as defined in Section 3.3. We perform this evaluation using the AST09 and ALG08 datasets since they differ in a variety of important properties, e.g., number of responses and skills.
As baseline approaches, we train BKT models using EM and OptimNN without any sort of explicit biasing of the learned parameters. We compare to training BKT using EM after initializing the guess and slip values to 0.1 (i.e., EM-init) (Pardos and Heffernan, 2010). For OptimNN-Reg, we use \(\lambda _1 = \lambda _2 = \lambda _3 = 0.25\) and \(\lambda _4 = 0.002\). For BKTransformer, we use \(\lambda _1 = \lambda _2 = \lambda _3 = 10\), \(\lambda _4 = 0\), and \(\lambda _5 = \lambda _6 = 1\). We do not consider CGD, as it is not easily adaptable to these preferences, or SGD, as we find it to be numerically unstable when adding penalty terms to the loss function. Other deep KT methods cannot be evaluated in this manner, so they are not considered for this evaluation.
6. Results
6.1. Comparisons with OptimNN
We compare the performance of OptimNN in predicting student correctness compared to different BKT optimization techniques: EM, CGD, and SGD on held-out test sets for the four chosen datasets, with the results shown in Table 2. To fit BKT parameters on these datasets, OptimNN shows decreased RMSE compared to all prior methods, with an average improvement of 4.0% over EM, 24.2% over CGD and 1.8% over SGD (where results are available for each method).
Compared to other methods, OptimNN shows the highest improvements across KT-IDEM and ILE,
with an extended set of learned model parameters. For instance, to fit KT-IDEM/ILE on the AST09
dataset, OptimNN shows relative improvement in terms of RMSE over EM by 8.2%. While OptimNN
is comparable to SGD on AST09, it outperforms SGD in statistically significant fashion on ALG08,
AST12 and BRI08. We do not report results for KT-IDEM and ILE on the remaining datasets using EM
as that demands over 200 GB of memory (i.e., RAM) for fitting using pyBKT, which is
unreasonable.
6.2. Comparisons with BKTransformer
Similarly to the evaluation of OptimNN, we compare the performance of BKTransformer in student correction prediction against deep KT and BKT baselines across the four chosen datasets in Table 3. We report the AUC and root mean-squared error (RMSE) for each dataset and method on the test set. On average, BKTransformer outperforms DKT by 0.5%, SAKT by 1.1%, and BKT-EM by 7.0% in terms of AUC.
Specifically, BKTransformer achieves the largest improvement in performance metrics on AST09, 1.2-10.6% in AUC over other methods, with smaller improvements on ALG08 and BRI08, compared to other methods. On AST12, DKT outperforms BKTransformer by 0.7% in RMSE.
Interestingly, while BKTransformer is based on SAKT and simply augments it using the BKT parameters, we believe that there are minor gains in metrics (e.g., in AST09/BRI08) largely due to the scaffolding that the BKT forward update provides (even though the BKT parameters themselves are variable over time). By constraining the ways in which the probabilities are computed through BKT and via penalties on the changing BKT parameters, we ensure that there are reasonable probabilistic processes governing the ways in which the correctness probability is computed. Intuitively, we can liken this to an implicit regularization of the correctness probabilities provided through BKT, which is a well-known and accepted structure governing the knowledge tracing problem.
To analyze this “regularization” hypothesis, we examine the tradeoff between the training binary cross entropy loss (which regularization is known to increase) and the RMSE on the evaluation dataset (which, in the case of overfitting, regularization is known to decrease). In Figure 3, we show the training loss over the duration of training for BKTransformer and SAKT, where BKTransformer plateaus at a greater eventual training loss. This lends credibility to the idea that the BKT forward pass may serve as an implicit regularization of the correctness probability prediction problem.
6.3. Fitted Parameter Analyses
We examine the generated parameters of BKTranformer, OptimNN, OptimNN-Reg, EM, and EM-init when fitting BKT on AST09 and ALG08. The method that minimizes the percentage of parameters that violate Rules 1-3 (i.e., rule violation percentage, or RVP) is deemed to be the least “degenerate” (Baker et al., 2008).
The results are shown in Table 4. Based on the average RVP for all three rules, OptimNN-Reg and BKTransformer demonstrate 0% RVP on the AST09 dataset, compared to OptimNN’s 1.2%, EM-init’s 2.1%, and EM’s 3.3%. On ALG08, BKTransformer and OptimNN-Reg’s improvement over other methods is large; they have a RVP of 0.0% and 1.2% respectively, whereas OptimNN has 23.3%, EM-init has 16.9%, and EM has 19.4%. Note that despite the large reduction in the number of rule violations, OptimNN-Reg displays similar AUC across the held-out test set compared to OptimNN, with a minor decrease of 0.003 on ALG08. Similarly, BKTransformer performs as well if not better than SAKT (Table 3). Across both datasets, SGD consistently shows the highest number of violations.
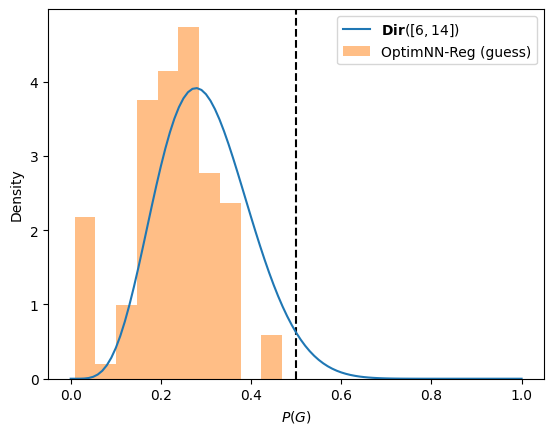
Further, we verify OptimNN-Reg’s capability to specify a prior over one or more of the BKT parameters on the AST09 dataset. We opt to use the Dirichlet distribution such that \(\mathrm {[guess, 1 - guess]} \sim \mathbf {Dir}([6, 14])\) as an example, although this may not necessarily be desirable in practise depending on the skill or dataset. To verify that the specified distribution is roughly matched based on the penalty term assigned in Equation \eqref{eqn:reg} by OptimNN-Reg, we plot the distribution of generated guess rates across skills and compare it to the probability density function of the chosen Dirichlet prior in Figure 4. We observe that the histogram of generated guess rates roughly matches the Dirichlet distribution, with the exception of higher guess rates that violate Rule 2. Note that while this can be used with BKTransformer, its utility may be lower since the intention is to vary parameters over time for additional expressive capability; hence, we do not evaluate this with BKTransformer.
6.4. Analysis of Parameter Evolution in BKTransformer
One of the key foci of this work is interpretability of the generated BKT parameters and mastery state. In this pursuit, we examine the way in which BKTransformer formulates its correctness and mastery predictions by examining how the BKT parameters are produced and varied over time. We choose two test student sequences from the ASSISTments 2009-10 Skill Builder (AST09) dataset. These sequences are chosen to show common or interesting patterns of student problem solving, and the resulting output is shown in Figure 5.
For Figure 5 (left), we analyze each segment of the sequence based on the attempted skill. Between \(t = 0\) to \(t = 2\), the student attempts the skill corresponding to “adding and subtracting fractions” (purple dot), where the series of consecutive correct responses lead to an increasing mastery \(P(L_t)\) and correctness probability \(P(\mathrm {obs}_t)\) approaching 1.
Following this, the student attempts “multiplying fractions” (as yellow dot), answering 3 questions consecutively incorrectly and then correctly. From \(t = 3\) to \(t = 5\), as the student answers incorrectly, the predicted correctness \(P(\mathrm {obs}_t)\) and mastery probability \(P(L_t)\) drop by over 20%, alongside an increase in the slip probability \(P(S)_t\) by roughly 10% and a decrease in the learn rate \(P(T)_t\) and guess rate \(P(G)_t\). These are reasonable since recent incorrect responses could indicate an increased probability of “slipping” on a question, with possibly less chance of attaining mastery or guessing the correct answer given lack of mastery.
At \(t = 9\), the student correctly attempts “dividing fractions” (as turquoise dot), and at \(t = 10, 11\), the student again correctly answers two questions from “adding and subtracting fractions”. As expected, the mastery \(P(L_t)\) and correctness probability \(P(\mathrm {obs}_t)\) are high at \(t = 10,11\) given past successful attempts. Interestingly, while the learn (\(P(T)_t\)) and guess (\(P(G)_t\)) probabilities at \(t = 10,11\) are comparable to the segment from \(t = 0\) to \(t = 2\), the slip probability \(P(S)_t\) is increased.
In Figure 5 (right), we demonstrate a sequence similar to the motivating example provided in Section 4.1. In this situation, a student attempts a single skill incorrectly 25 consecutive times, and we observe that BKTransformer correctly predicts student correctness through \(P(\mathrm {obs}_t)\) at all timesteps. Importantly, both the mastery \(P(L_t)\) and correctness probability \(P(\mathrm {obs}_t)\) reduce with each incorrect response and tend towards zero, indicating no eventual likelihood of mastery or correctness. Alongside this, we observe that the generated, temporally-evolving slip rate \(P(S)_t\) tends to rise with incorrect responses. This supports the intuition that despite a higher prior of mastery probability at earlier timesteps, each incorrect response increases the belief of the student “slipping” and answering incorrectly on subsequent questions.
6.5. Ablation Studies
We examine the effect of varying hyperparameters on the performance of the proposed methods. Specifically, we ablate the effect of the number of layers, hidden size, and learning rate of the neural network and transformers. For methods that are sensitive to hyperparameters, we expect that varying these hyperparameters would have a large impact on performance metrics. To evaluate this, we leverage the AST09 dataset and choose AUC and RMSE as the metrics.
In Table 5, we show the effect of varying the number of neural network layers and the hidden size on OptimNN. For all embedding dimensions and for all layers, there is effectively no difference on the performance in any metric, which illustrates that our method is relatively insensitive to hyperparameter changes and would require minimal to no hyperparameter tuning for such datasets. When the embedding dimension is significantly reduced, the performance across all metrics begins to drop, but the drop is relatively minimal and performance remains equal or better relative to other BKT optimization techniques. We believe that this is reasonable since BKT fundamentally imposes a simple structure on the knowledge tracing problem, and parameterization far beyond the number of BKT parameters is unlikely to result in far better optima.
| Emb Dim. | AUC | RMSE
|
|---|---|---|
| 8 | 0.833 | 0.379 |
| 16 | 0.837 | 0.377 |
| 32 | 0.839 | 0.375 |
| 64 | 0.839 | 0.375 |
| 128 | 0.838 | 0.375 |
| 256 | 0.838 | 0.376 |
| Emb Dim. | AUC | RMSE
|
|---|---|---|
| 8 | 0.832 | 0.380 |
| 16 | 0.834 | 0.378 |
| 32 | 0.840 | 0.375 |
| 64 | 0.838 | 0.377 |
| 128 | 0.837 | 0.376 |
| 256 | 0.837 | 0.378 |
We compare the sensitivity of OptimNN and SGD to the configuration of the optimizer. For both methods, we leverage the Adam optimizer, and we ablate the effect of the learning rate. We choose 4 learning rates, including commonly used or default learning rates for Adam: 1e-4, 5e-4, 1e-3 (Adam default), and 1e-2. We show the resulting AUC on the test set in Figure 6, where OptimNN yields an optimal model after simply 1 epoch of training regardless of the learning rate and SGD fails to do so within 12 epochs for 3 of 4 learning rates.
In Table 6, we show the effect of varying the number of layers and hidden size on BKTransformer. An optimal choice for the number of layers seems to be 2 or 3. Despite that, the largest difference in AUC is relatively small for any embedding dimension over 32, which again indicates that BKTransformer is relatively insensitive to reasonable hyperparameter changes and would require minimal tuning to achieve strong performance on such datasets.
We observe sharp performance dropoff with embedding dimensions smaller than 32. This is a reasonable outcome based on two intuitions. Firstly, as the parameterization of the parameter generation network becomes lower, deep neural networks tend to be able to reasonably learn a smaller set of functions using gradient descent, which lead to more suboptimal models. Secondly, as the parameterization decreases, we empirically observe performance closer to other low-parameterization methods such as BKT (EM) or BKT (SGD). Interestingly, for the lowest embedding dimension of 8, we observe that BKTransformer performs worse than all other BKT optimization techniques except for CGD, which may suggest that underparameterization of the transformer architecture may lead to worse performance than of simpler architectures.
| Embedding Dim. | AUC | RMSE
|
|---|---|---|
| 8 | 0.781 | 0.431 |
| 16 | 0.803 | 0.391 |
| 32 | 0.880 | 0.355 |
| 64 | 0.893 | 0.339 |
| 128 | 0.886 | 0.347 |
| 256 | 0.890 | 0.341 |
7. Discussion and Conclusion
We demonstrate that the proposed neural network-based optimization technique, OptimNN, outperforms EM, CGD, and SGD in terms of AUC across all chosen BKT variants and datasets. Especially on BKT extensions, OptimNN shows an even larger margin of improvement compared to other approaches. This demonstrates that OptimNN is able to discover more optimal local minima with respect to performance than other approaches.
The proposed extension based on transformer modeling, BKTransformer, improves upon both BKT and either equals or surpasses deep KT baselines in terms of several performance metrics across multiple datasets. Presenting a practical framework that rivals or surpasses existing deep KT methods in performance across a variety of metrics and datasets, we show that BKTransformer importantly retains more interpretability and explainability through the generation of temporally-evolving BKT parameters. While we leverage a flexible multi-head attention mechanism that allows for non-Markovian learning and parameter sharing across skills, we believe that the implicit regularizing nature of enforcing a BKT structure to the correctness predictions provides an improved interpretable nature to our model.
Based on an analysis of the fitted BKT parameters, we conclude that both BKTranformer and OptimNN-Reg show the least violations of guidelines proposed in Baker et al. (2008) and van de Sande (2013) compared to EM, EM-init, and OptimNN, with a high degree of flexibility in the possible preferences and rules. Moreover, analyzing the evolution of BKT parameters generated over student sequences, it is clear that the generated parameters support intuition of how parameters should evolve based on the sequence of correct and incorrect responses.
We believe that this work provides a layer of interpretability beyond what deep learning currently offers. Specifically, beyond knowing that the probability of correctness or incorrectness has increased, our technique offers a 4-parameter probabilistic explanation of why exactly it has offered that prediction. There may be cases in which the slip rate is large or there may be cases where the forget rate is large; we believe both these cases can lead to different interpretations of low probabilities of correctness and could lead to different conclusions about learning.
Limitations and Future WorkWhile we believe our work succeeds in providing a layer of interpretability over prior techniques alongside retaining impressive performance, it has many limitations that we propose to explore in future work. These including improving interpretability in the neural network layers and transformers; for instance, can we examine and regularize the attention patterns based on prior knowledge? Currently, we are unable to fully interpret the components of BKTransformer that precede the BKT “layer”, which prevents us from understanding how and why BKT parameters over time evolve as they do. Another important analysis is to discover which preferences and rules are most necessary and effective for use with our proposed technique; while we show that traditional “rules” work well, it is worth exploring a more restrictive set of rules for a more flexible method like BKTransformer. Finally, there exist no guarantees that the given rules are followed, and for some rules that are challenging to optimize (e.g., far away from the “naive” or “easy” solution), hyperparameter tuning might be required to find the appropriate penalty weight.
References
- Abdelrahman, G. and Wang, Q. 2022. Deep graph memory networks for forgetting-robust knowledge tracing. Institute of Electrical and Electronics Engineers Transactions on Knowledge and Data Engineering 35, 8, 7844–7855.
- Aleven, V. A. and Koedinger, K. R. 2002. An effective metacognitive strategy: learning by doing and explaining with a computer-based cognitive tutor. Cognitive Science 26, 2, 147–179.
- Anzai, Y. and Simon, H. A. 1979. The theory of learning by doing. Psychological Review 86, 2, 124.
- Bach, S., Binder, A., Montavon, G., Klauschen, F., Müller, K.-R., and Samek, W. 2015. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLOS ONE 10, 7 (07), 1–46.
- Badrinath, A., Wang, F., and Pardos, Z. 2021. pybkt: An accessible python library of bayesian knowledge tracing models. In Proceedings of the 14th International Conference on Educational Data Mining (Educational Data Mining 2021), S. Hsiao and S. Sahebi, Eds. International Educational Data Mining Society, 468–474.
- Baker, R. S. J. d., Corbett, A. T., and Aleven, V. 2008. More accurate student modeling through contextual estimation of slip and guess probabilities in bayesian knowledge tracing. In Intelligent Tutoring Systems, B. P. Woolf, E. Aïmeur, R. Nkambou, and S. Lajoie, Eds. Springer Berlin Heidelberg, Berlin, Heidelberg, 406–415.
- Bloom, B. S. 1984. The 2 sigma problem: The search for methods of group instruction as effective as one-to-one tutoring. Educational Researcher 13, 6, 4–16.
- Chang, K.-m., Beck, J., Mostow, J., and Corbett, A. 2006. A bayes net toolkit for student modeling in intelligent tutoring systems. In Intelligent Tutoring Systems, M. Ikeda, K. D. Ashley, and T.-W. Chan, Eds. Springer Berlin Heidelberg, Berlin, Heidelberg, 104–113.
- Chollet, F. et al. 2015. Keras.
https://keras.io. - Corbett, A. T. and Anderson, J. R. 1994. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction 4, 4, 253–278.
- Gardner, J. and Brooks, C. 2017. Statistical approaches to the model comparison task in learning analytics. In Joint Proceedings of the Workshop on Methodology in Learning Analytics (MLA) and the Workshop on Building the Learning Analytics Curriculum (BLAC) co-located with 7th International Learning Analytics and Knowledge Conference (LAK 2017), Vancouver, Canada, March 13th-14th, 2017, Y. Bergner, C. Lang, G. Gray, S. D. Teasley, and J. C. Stamper, Eds. CEUR Workshop Proceedings, vol. 1915. CEUR-WS.org.
- Ghosh, A., Heffernan, N., and Lan, A. S. 2020. Context-aware attentive knowledge tracing. In Proceedings of the 26th Association for Computing Machinery Special Interest Group on Knowledge Discovery in Data International Conference on Knowledge Discovery & Data Mining. Association for Computing Machinery, New York, NY, USA, 2330–2339.
- Ha, D., Dai, A. M., and Le, Q. V. 2017. Hypernetworks. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net.
- Hestenes, M. R. and Stiefel, E. 1952. Methods of conjugate gradients for solving. Journal of Research of the National Bureau of Standards 49, 6, 409.
- Hochreiter, S. and Schmidhuber, J. 1997. Long short-term memory. Neural Comput. 9, 8 (Nov.), 1735–1780.
- Khajah, M., Lindsey, R. V., and Mozer, M. C. 2016. How deep is knowledge tracing? In Proceedings of the 9th International Conference on Educational Data Mining, T. Barnes, M. Chi, and M. Feng, Eds. International Educational Data Mining Society, 94–101.
- Kingma, D. P. and Ba, J. 2015. Adam: A method for stochastic optimization. In International Conference on Learning Representations (ICLR). ArXiv, Ithaca, NY, 1–13.
- Labra, C. and Santos, O. C. 2023. Exploring cognitive models to augment explainability in deep knowledge tracing. In Adjunct Proceedings of the 31st Association for Computing Machinery Conference on User Modeling, Adaptation and Personalization. Association for Computing Machinery, New York, NY, USA, 220–223.
- Levinson, S. E., Rabiner, L. R., and Sondhi, M. M. 1983. An introduction to the application of the theory of probabilistic functions of a markov process to automatic speech recognition. Bell System Technical Journal 62, 4, 1035–1074.
- Liu, Q., Huang, Z., Yin, Y., Chen, E., Xiong, H., Su, Y., and Hu, G. 2019. Ekt: Exercise-aware knowledge tracing for student performance prediction. Institute of Electrical and Electronics Engineers Transactions on Knowledge and Data Engineering 33, 1, 100–115.
- Lu, Y., Wang, D., Meng, Q., and Chen, P. 2020. Towards interpretable deep learning models for knowledge tracing. In Artificial Intelligence in Education, I. I. Bittencourt, M. Cukurova, K. Muldner, R. Luckin, and E. Millán, Eds. Springer International Publishing, Cham, 185–190.
- Nagatani, K., Zhang, Q., Sato, M., Chen, Y.-Y., Chen, F., and Ohkuma, T. 2019. Augmenting knowledge tracing by considering forgetting behavior. In The World Wide Web Conference. Association for Computing Machinery, New York, NY, USA, 3101–3107.
- Nakagawa, H., Iwasawa, Y., and Matsuo, Y. 2019. Graph-based Knowledge Tracing: Modeling Student Proficiency Using Graph Neural Network . In 2019 Institute of Electrical and Electronics Engineers/Web Intelligence Consortium/Association for Computing Machinery International Conference on Web Intelligence (WI). Institute of Electrical and Electronics Engineers Computer Society, Los Alamitos, CA, USA, 156–163.
- Pandey, S. and Karypis, G. 2019. A self-attentive model for knowledge tracing. In Educational Data Mining 2019 - Proceedings of the 12th International Conference on Educational Data Mining, C. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, 384–389.
- Pardos, Z. A. and Heffernan, N. T. 2009. Detecting the learning value of items in a randomized problem set. In Proceedings of the 2009 Conference on Artificial Intelligence in Education: Building Learning Systems That Care: From Knowledge Representation to Affective Modelling, V. Dimitrova, R. Mizoguchi, B. du Boulay, and A. Graesser, Eds. IOS Press, NLD, 499–506.
- Pardos, Z. A. and Heffernan, N. T. 2010. Navigating the parameter space of bayesian knowledge tracing models: Visualizations of the convergence of the expectation maximization algorithm. In Educational Data Mining 2010, The 3rd International Conference on Educational Data Mining, Pittsburgh, PA, USA, June 11-13, 2010. Proceedings, R. S. J. de Baker, A. Merceron, and P. I. Pavlik, Eds. www.educationaldatamining.org, 161–170.
- Pardos, Z. A. and Heffernan, N. T. 2011. Kt-idem: Introducing item difficulty to the knowledge tracing model. In User Modeling, Adaption and Personalization, J. A. Konstan, R. Conejo, J. L. Marzo, and N. Oliver, Eds. Springer Berlin Heidelberg, Berlin, Heidelberg, 243–254.
- Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Köpf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J., and Chintala, S. 2019. Pytorch: an imperative style, high-performance deep learning library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems. Curran Associates Inc., Red Hook, NY, USA.
- Pelánek, R. 2017. Bayesian knowledge tracing, logistic models, and beyond: an overview of learner modeling techniques. User Modeling and User-Adapted Interaction 27, 3 (Dec), 313–350.
- Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L., and Sohl-Dickstein, J. 2015. Deep knowledge tracing. In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 1. MIT Press, Cambridge, MA, USA, 505–513.
- Rai, D., Gong, Y., and Beck, J. 2009. Using dirichlet priors to improve model parameter plausibility. In Educational Data Mining - EDM 2009, Cordoba, Spain, July 1-3, 2009. Proceedings of the 2nd International Conference on Educational Data Mining, T. Barnes, M. C. Desmarais, C. Romero, and S. Ventura, Eds. International Educational Data Mining Society, 141–150.
- Ritter, S., Anderson, J. R., Koedinger, K. R., and Corbett, A. 2007. Cognitive tutor: Applied research in mathematics education. Psychonomic Bulletin & Review 14, 2, 249–255.
- Santoro, A., Bartunov, S., Botvinick, M., Wierstra, D., and Lillicrap, T. 2016. Meta-learning with memory-augmented neural networks. In Proceedings of the 33rd International Conference on International Conference on Machine Learning - Volume 48. JMLR.org, 1842–1850.
- Tong, S., Liu, Q., Huang, W., Hunag, Z., Chen, E., Liu, C., Ma, H., and Wang, S. 2020. Structure-based knowledge tracing: An influence propagation view. In 2020 Institute of Electrical and Electronics Engineers International Conference on Data Mining (ICDM). Institute of Electrical and Electronics Engineers, 541–550.
- van de Sande, B. 2013. Properties of the bayesian knowledge tracing model. Journal of Educational Data Mining 5, 2 (Jul.), 1–10.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., and Polosukhin, I. 2017. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems. Curran Associates Inc., Red Hook, NY, USA, 6000–6010.
- Wang, Z., Feng, X., Tang, J., Huang, G. Y., and Liu, Z. 2019. Deep knowledge tracing with side information. In Artificial Intelligence in Education, S. Isotani, E. Millán, A. Ogan, P. Hastings, B. McLaren, and R. Luckin, Eds. Springer International Publishing, Cham, 303–308.
- Yeung, C.-K. 2019. Deep-irt: Make deep learning based knowledge tracing explainable using item response theory. In Proceedings of The 12th International Conference on Educational Data Mining (EDM 2019), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, 683–686.
- Yeung, C. K. and Yeung, D. Y. 2018. Addressing two problems in deep knowledge tracing via prediction-consistent regularization. In Proceedings of the 5th Association for Computing Machinery Conference on Learning @ Scale. Association for Computing Machinery, 5:1–5:10.
- Yin, Y., Liu, Q., Huang, Z., Chen, E., Tong, W., Wang, S., and Su, Y. 2019. Quesnet: A unified representation for heterogeneous test questions. In Proceedings of the 25th Association for Computing Machinery Special Interest Group on Knowledge Discovery in Data International Conference on Knowledge Discovery & Data Mining. Association for Computing Machinery, New York, NY, USA, 1328–1336.
- Yudelson, M. V. 2016. Individualizing bayesian knowledge tracing. are skill parameters more important than student parameters?. In Proceedings of the 9th International Conference on Educational Data Mining, EDM 2016, Raleigh, North Carolina, USA, June 29 - July 2, 2016, T. Barnes, M. Chi, and M. Feng, Eds. International Educational Data Mining Society, 46–53.
- Yudelson, M. V., Koedinger, K. R., and Gordon, G. J. 2013. Individualized bayesian knowledge tracing models. In Artificial Intelligence in Education, H. C. Lane, K. Yacef, J. Mostow, and P. Pavlik, Eds. Springer Berlin Heidelberg, Berlin, Heidelberg, 171–180.
- Zhang, L., Xiong, X., Zhao, S., Botelho, A., and Heffernan, N. T. 2017. Incorporating rich features into deep knowledge tracing. In Proceedings of the Fourth (2017) Association for Computing Machinery Conference on Learning @ Scale. Association for Computing Machinery, New York, NY, USA, 169–172.
A. Derivation for Motivating Example
Example A.1. For any set of non-degenerate learned BKT parameters, i.e., \(P(G) < 0.5, P(S) < 0.5\) with \(P(F) < 1 - P(T)\), and any timestep \(t \in [1, \infty )\)
\begin {align*} P(L_t) &= (1 - P(F)) P(L_{t-1} \mid \mathrm {obs}_{t-1}) + P(T) (1 - P(L_{t-1} \mid \mathrm {obs}_{t-1}))\\ &> P(T) \end {align*}
Proof. Given our restriction that \(1 - P(F) > P(T)\), we can derive:
\begin {align} P(L_t) &> P(T) P(L_{t-1} \mid \mathrm {obs}_{t-1}) + P(T) (1 - P(L_{t-1} \mid \mathrm {obs}_{t-1})) \\ &> P(T) (P(L_{t-1} \mid \mathrm {obs}_{t-1}) + 1 - P(L_{t-1} \mid \mathrm {obs}_{t-1})) \\ &> P(T) \end {align} □
B. Code References
The codebase is available publicly at the following public GitHub repository and the associated datasets are taken directly from their linked sources in the main paper:
https://github.com/abadrinath947/OptimNN.