Problem for Programming: Methods and Tradeoffs with Limited Labeled Data
Abstract
Understanding students’ learning of knowledge components (KCs) is an important educational data mining task and enables many educational applications. However, in the domain of computing education, where program exercises require students to practice many KCs simultaneously, it is a challenge to attribute their errors to specific KCs and, therefore, to model student knowledge of these KCs. In this paper, we define this task as the KC attribution problem. We first demonstrate a novel approach to addressing this task using deep neural networks and explore its performance in identifying expert-defined KCs (RQ1). Because the labeling process takes costly expert resources, we further evaluate the effectiveness of transfer learning for KC attribution, using more easily acquired labels, such as problem correctness (RQ2). Finally, because prior research indicates the incorporation of educational theory in deep learning models could potentially enhance model performance, we investigated how to incorporate learning curves in the model design and evaluated their performance (RQ3). Our results show that in a supervised learning scenario, we can use a deep learning model, code2vec, to attribute KCs with a relatively high performance (AUC \(>75\%\) in two of the three examined KCs). Further using transfer learning, we achieve reasonable performance on the task without any costly expert labeling. However, the incorporation of learning curves shows limited effectiveness in this task. Our research lays important groundwork for personalized feedback for students based on which KCs they applied correctly, as well as more interpretable and accurate student models.Keywords
1. Introduction
Modeling the state of students’ knowledge as they work, or student modeling, has great potential to benefit students and to provide insight to instructors and researchers (Ai et al., 2019, Muldner et al., 2015, Cen et al., 2006). To accomplish this, most student models have two requirements at a minimum: 1) a set of skills, or knowledge components (KCs, Koedinger et al. (2012)), that students are learning, and 2) a way to automatically assess what KC a student is practicing, and whether they have applied that KC correctly. Historically, this has been accomplished by creating problems, or problem sub-steps, that practice one KC at a time, which can be automatically assessed (e.g., fill-in-the-blank or multiple-choice questions, e.g., in datasets collected from ASSISTments Selent et al. (2016)). If a student gets the step correct, the student model knows they have demonstrated knowledge of the corresponding KC, and vice versa. However, in many domains, such as computer programming, students practice problems that require applying multiple KCs simultaneously, which cannot easily be broken down into automatically-assessed sub-steps (e.g. writing a function using loops, variables and conditionals). Similar challenges also exist in other domains, such as open-ended learning environments (Kinnebrew et al., 2014), game-based learning (Tobias et al., 2014), and natural language writing (McNamara et al., 2013) domains. In these situations, when a student gets the problem wrong, they may have still applied some KCs correctly but failed to apply others, causing them to get the problem wrong. In this case, a student model must determine which KCs the student applied correctly and which they applied incorrectly. We call this challenge the Knowledge Component attribution problem.
As an example, consider the context of this paper: computing education. Instructors often ask
students to write programs that combine a variety of KCs (e.g., related to conditionals, boolean
logic, and operators), which may take significant time and multiple attempts to complete
successfully. Students’ work (i.e., code submissions) is assessed automatically by test cases, but
these test cases often do not have a direct correspondence to individual KCs. As a result,
when a student submits code that is not fully correct, it is not clear which KCs they have
applied correctly and incorrectly. For example, consider two students writing a piece of
Java code to solve a problem. As part of that solution, the code must check whether the
variable age is in the range of 11 to 20, inclusive, and run code block A if so, or else run code
block B. Assume that two different students write code shown in Figure 1. In this example,
both solutions are incorrect, but for different reasons. The first submission has an issue of
misusing the || operator in the range, while the second submission has incorrect output
from the inversed logic under the two conditions. The two submissions are both incorrect,
but a student model should treat them differently, for instance, by giving them additional
practice with the concepts they are struggling with, not the ones they have successfully
demonstrated.
Prior work that has tried to solve what we call the KC attribution problem in programming has
raised three critical questions that we try to address in this paper: 1) The first question is how to define
and represent KCs in programming. Prior work on KC attribution in programming (Hosseini and
Brusilovsky, 2013, Rivers et al., 2016) has treated programming keywords and
identifiers (e.g., if and for) as proxies for KCs. While looking for the keyword if is a practical
solution, defining KCs in this way might not lead to a KC model that is nuanced enough to capture
more detailed aspects of student’s knowledge. For example, students might know how to apply in one
context, but not in another. In this work, we address this question by using domain experts to define
the KCs that will be assessed so that KCs are meaningful and consistent. In addition, after
defining and representing KCs, prior works have evaluated the success of KC attribution
by using learning curves (e.g., in Rivers et al. (2016), the authors checked
whether the attributed KCs fit ideal learning curves) instead of labeled KC correctness.
In this work, we directly provide hand-labeled KCs and create a ground truth dataset for
evaluation.1
2) The second question is, when KC attribution labels are limited, how do we still train a model for the
task we aim to solve? Specifically, in our context, we use the transfer learning strategy to take the data
of student submission correctness and use the information for the KC attribution task. KC attribution
can be formulated as a classification problem, requiring a training dataset with expert-authored labels
indicating the practice of the individual KCs, and it calls for information transferred from another
relatively effortless source. Prior work (Rivers et al., 2016) has solved this using
a data-driven hint system (Rivers and Koedinger, 2017), which learns a model of correct
and incorrect behavior from prior student data. In our paper, we address the question with
transfer learning and evaluate how transfer learning performs for the KC attribution task. 3)
The third question is aligning the KC attributions with learning theory. It was shown that
token-based KCs in prior work often do not behave like KC ought to. I.e., the power law
of practice postulates that a student’s performance in a particular KC increases with the
number of KC practice opportunities (Snoddy, 1926) (details in Section 2.1). Students’
overall error rate in practicing a KC should drop at an exponential rate as they practice
more, fitting into a curve (i.e., learning curve). Our method further incorporates the expected
learning curve into the deep learning model, and we evaluate the performance of models after
incorporation.
In this paper, we present methods for addressing the KC attribution problem in programming, and explore tradeoffs in addressing the above questions. Our analysis focuses on the publicly available CodeWorkout dataset (Edwards and Murali, 2017), consisting of interaction data from students in an introductory level Computer Science course. Our goal is to solve the KC attribution problem: to determine, given a student’s incorrect code, which relevant KC(s) they have applied correctly and incorrectly. We start by investigating how effectively a deep learning model can solve this problem when trained on a corpus of expert-labeled data. Our results show that compared with the traditional shallow models, a deep learning model such as code2vec (Alon et al., 2019) performs better, even with limited labeled data (students \(n = 48\)). To address the challenge of annotating code submissions with KC labels, we not only examined the performance of the deep learning model with different sizes of labeled data. We also employ transfer learning (Torrey and Shavlik, 2010) to address the challenge of using transferred information from submission correctness labels to train a model without hand-labeling any data. We also built multi-task learning (Caruana, 1997) models to investigate the information transferred between the two tasks (i.e. KC attribution and KC relevance detection using submission correctness). Without using any hand-labeled data, our model was still able to achieve better classification results than our baseline models that did have access to labeled data, though it performed worse than the deep learning model in the supervised scenario which used the labeled data. To further explore possible improvements on the transfer learning scenario for better performance, inspired by prior work integrating quantitative properties of KCs into machine learning models (e.g., Cen et al. (2006), Shi et al. (2023)), we also explore how to incorporate some of the theoretical properties of KCs into the model, specifically the power law of practice, described in Section 3.2.5. Our results are mixed: learning curves in the best possible scenario may bring improvement in the KC attribution task on certain KCs.
In summary, we answer three research questions (RQs) in the paper as our contributions:
- RQ1: How do deep learning methods that analyze students’ code perform on the KC attribution problem, how does this compare to traditional models, and how does this performance vary with the amount of available training data?
- RQ2: To what extent can information learned from other, more readily available labels (i.e., submission correctness) be applied to solving the KC attribution problem?
- RQ3: To what extent does incorporating ideal learning curves of KCs improve the performance of KC attribution?
2. Related Work
2.1. Knowledge Component and Learning Curve
In our work, knowledge components (KCs) are a set of constructs referring to the skills students learn when practicing programming through open-ended problems. KCs are a cognitive concept introduced in the Knowledge-Learning-Instruction (KLI) framework (Koedinger et al., 2012), defined as a set of unobservable states in the learning process through observable instructional (e.g., lectures) and assessment (e.g., tests) events. KCs serve as a bridge between instructional and assessment events. When instructors teach through instructional events, students learn from them and internalize them as their own knowledge, measured by properly sized pieces as KCs. KCs are then evaluated through assessment events such as exams and tests and probed through these observable activities. While KCs can represent different knowledge, we focus on KCs in a programming context. For example, “knowing how to write an ‘if’ statement to solve a problem with two possible conditions” is a concrete procedural skill (KC) that we explore in this study. KCs can be represented in different granularity. For example, knowing “how to represent a range of variables in an ‘if’ condition” is a skill frequently used in students’ code, and a finer-grained skill can be knowing “the difference between open and closed intervals”. To associate KCs with the problems practicing KCs, Barnes et al. used Q-matrix to represent their relationships (Barnes, 2005). Rows and columns in Q-matrices are problems and KCs respectively, and the corresponding cells in the matrices are zero/one binaries. A one-value in a cell means the corresponding KC is practiced in the problem. Our paper follows this representation in the KC defining and labeling process.
Knowledge components can be used in a variety of educational applications. In learning analytics, knowing the status of students’ knowledge can help teachers make pedagogical decisions. For example, the Open Learner Model (Barria-Pineda et al., 2018) uses KCs to guide students to needed learning activities. Researchers also benefit from knowing students’ mastery of KCs and can derive insights such as their process of studying worked examples and knowledge transfer (Salden et al., 2009). Students’ mastery of KCs can also be used to show students how they learn as visual (Labra and Santos, 2023) and textual (Graesser et al., 2018) feedback. The information about which KCs are correctly and incorrectly practiced can also be used for personalized instruction by guiding problem recommendation for students (Aleven and Koedinger, 2013).
While KCs can be defined by expert definitions (as introduced in Section 3.1), the demonstration of KCs by students is a cognitive process that cannot be observed directly (Koedinger et al., 2012). However, the definition allows KC to be inferred from students’ performance data (Koedinger et al., 2012), supported by cognitive science theory. For instance, the power law of practice states that if the set of KCs is well defined (i.e. in a well-defined cognitive model), the error rate of students practicing the individual KCs decreases at an exponential rate (Newell and Rosenbloom, 2013, Snoddy, 1926, Cen et al., 2006). It has been mathematically modeled as \[Y=aX^b\] , where \(Y\) refers to the error rate, \(X\) refers to the number of opportunities students practiced on the KC, and \(a\) and \(b\) are parameters of the curve, controlling the starting error rate and learning rate, respectively. We focus on how the learning curve property can be used to further help the KC attribution model training process.
2.2. Knowledge Component Attribution
It is important to distinguish the KC attribution problem from the common task of knowledge tracing (KT, see Corbett and Anderson (1994)). In KC attribution, the focus is on the student’s observable work (e.g., a submission to a programming problem), and the task is to determine whether that submission correctly or incorrectly applies a set of KCs; i.e., does it serve as evidence for or against a student’s mastery of these KCs. By contrast, knowledge tracing typically takes as input a set of observations of student’s correct/incorrect application of a KC, and tries to assess the unobservable state of a student’s mastery of that KC, to make predictions about future performance (Corbett and Anderson, 1994, Piech et al., 2015). In other words, KC attribution is in some sense a prerequisite to knowledge tracing. In learning environments with short problems or steps that practice one KC at a time, this step is simple. However, in domains such as programming, where problems may practice many interrelated KCs, this information is not available. To address this, prior work, such as Code-DKT has proposed simply using the problem ID to represent each problem, and using a deep neural network to learn the relationships between problems (Shi et al., 2022). While this approach has been quite successful at predicting future performance on problems, it does not actually represent students’ underlying mastery of specific, human-interpretable KCs, making it less useful to researchers and instructors. Such models, in other words, can say that a student might fail a problem, but they cannot say why, or what skills the student must practice to get it right. However, if we can solve the KC attribution problem, as this work takes a step toward doing, these KT models would be far more interpretable, and possibly more accurate, by reasoning directly about KCs.
Prior works have been addressing the KC attribution problem. For example, MacLellan et al. proposed a three-step method to cluster student work in an educational game into patterns and clustered them into KCs (MacLellan et al., 2015). The game aims to teach students three concepts of structural stability and balance. Their formulation of the KC attribution task has similarities with ours, as they attribute human-defined concepts from student submissions of the game, while we attribute defined KCs from code submissions. Their clustering methods work for KCs relatively less intertwined. However, the attribution problem could be more complicated for specific domains, such as computing education. Previous works in computing education have been leveraging the content submitted by students to identify their understanding of programming KCs. Traditionally, programming concepts have been taught in a step-by-step fashion (e.g., Lisp Tutor Anderson and Reiser (1985)), which allows KC attributed by step correctness. However, more recent programming tutoring systems have been prompting students to write code in an open-ended way, and in such scenarios, more advanced methods for KC attribution are required. For example, Rivers et al. leveraged canonicalized code submissions and extracted the nodes in abstract syntax trees (ASTs) for an automatic hint system (Rivers and Koedinger, 2017), and they used the hints to identify nodes as KCs to attribute when students make incorrect submissions. Similarly, Hosseini et al. introduced JavaParser, which also considered nodes in ASTs from student submissions as KCs (Hosseini and Brusilovsky, 2013). However, KCs defined as programming nodes don’t follow the power law of practice (as seen in Shi et al. (2023)) and may represent many different skills (as introduced in Section 1). Our deep learning-based method focuses on expert-defined KCs instead of node KCs and achieves the KC attribution task.
2.3. Student Modeling in Computing Education
Source code analysis has been a pivotal tool in understanding and modeling student performance in CS. Jin et al. (2012)’s approach to student modeling in CS education involved using the structure of code for generating programming hints. This method leveraged linkage representations reflecting code structure. Yudelson et al. (2014) focused on extracting code features from a Java MOOC to predict student success and recommend appropriate problems. They use atomic code features for problem recommendation but did not evaluate its model directly on KT tasks. In Rivers et al. (2016) work, they employed abstract syntax trees (ASTs) for the generation of KCs and hint creation within a programming tutor, a significant step in applying KCs in practical educational tools. Their work mirrors Nguyen et al. (2019)’s application of refinement techniques to digital learning games by modeling KCs by problem types. This highlights the expanding scope of student modeling, from traditional learning environments to interactive digital platforms. Furthermore, Rivers et al. analyzed student learning curves using ASTs and error rate curves presents an innovative method of extracting meaningful KCs from student code (Rivers et al., 2016). Similarly, Wang et al. (2017) worked with “hour of code” exercise using a deep learning method, however, the code representations used are natural language based and do not contain structural information derived from student code. These diverse methods in student modeling within CS education, from linkage representations to advanced deep learning techniques, demonstrate the field’s evolving complexity and potential. Our approach builds upon these foundations by using code2vec, a deep neural network that extracts structural information to attribute KCs in complex programming tasks, addressing the challenge of assessing multiple KCs simultaneously.
Student modeling in computing education has been evolving, with a shift from predicting compiler errors (Kamberovic et al., 2023) to actively enhancing student learning experience. A recent systematic literature review by (Hellas et al., 2018) showed an increase interest in predicting student performance research in computing education, as well as an increase in variety of data-driven techniques used. In (Kamberovic et al., 2023) work, they initially addressed student modeling with a focus on predicting compiler errors, demonstrating the potential for personalized tasks and code improvements. Other recent work (Morshed Fahid et al., 2021) introduced a progression trajectory-based student modeling framework to compared diverse student program to expert solutions and found three distinct clusters to better understanding student behaviors in individual programming activities.
Some direct applications of student modeling are built upon the aforementioned work. For example, some recent works have focused on extending hint generation for block-based programming languages (Fein et al., 2022, Price et al., 2017, Morshed Fahid et al., 2021). In (Fein et al., 2022), the authors developed a tool for generating next-step hints for Scratch by comparing student attempts with model solutions with AST encoding. A common technique in these systems is the use of edit distance calculations between students code states and expert solutions (Morshed Fahid et al., 2021, Paassen et al., 2018, Rivers and Koedinger, 2017). Similarly, (Gonçalves and Santos, 2023) developed a tool for generating contextual hints for Java exercises, moving from typical error detection to facilitating engaged student learning. Another body of work on the application of student modeling has focused on clustering novice programming behavior into student learning trajectories (Jiang et al., 2022, Blikstein, 2011, Maniktala et al., 2020, Perkins and Martin, 1986, Wiggins et al., 2021, Morshed Fahid et al., 2021) and to identify coding misconceptions (Emerson et al., 2020). These applications are crucial for informing pedagogical decisions and improving learning outcomes, and they largely rely on automatic and accurate attribution of KCs. Our work on the KC attribution task serves as an upstream improvement, and we look to further strengthen these applications through further study.
2.4. Deep Learning in Education
The recent development of deep learning technology has improved the performance of tasks not only in educational data mining domains, but also in more general software engineering areas, such as code summarization, program name detection, and bug detection areas. For example, Allamanis et al. (2016) introduced a convolutional neural network (CNN) model to summarize code snippets by integrating attention mechanisms. In 2019, Alon et al. (2019) proposed the code2vec model to extract programming code information from abstract syntax trees (ASTs) as code paths (Alon et al., 2018), and use a simple attention layer to calculate the importance of code paths, for the classification of method names. These methods fueled recent research on data mining in computing education. Shi et al. (2021) leveraged the code2vec model for student error clustering in an unsupervised way and further classified student bugs with a semi-supervised method in a later work (Shi et al., 2021, Shi and Price, 2022). Fein et al. (2022) and Hoq et al. (2023) used the code2vec model for code classification tasks and improved the performance from traditional text mining models. The model has also been incorporated into student performance prediction (Mao et al., 2021) and KT (Shi et al., 2022) tasks, making it promising for more complex student modeling tasks such as KC discovery (Shi, 2023, Shi et al., 2023). Our research further extends this line of research to leverage students’ code features and educational theory for the KC attribution task.
3. Method
3.1. Defining Q-matrices
The first step before attributing KCs is to define a set of KCs that is relevant for our dataset from an introductory computing course. The definition of KCs could be achieved manually via a variety of methods. One common way to define KCs is through cognitive task analysis (CTA, Clark et al. (2008)). One key step of CTA is knowledge elicitation (Cooke, 1994), where a knowledge engineer works with the domain experts to codify the knowledge into a structured format. Although some recent work has provided a way to extract KCs automatically, the KCs are not directly interpretable as programming code and still need further revising (Shi et al., 2023). In this paper, we decided to manually extract KCs for interpretability considerations, but in a simpler way than CTA. Instead of having specific knowledge engineers elicit the process of solving the problem, we had experts (authors who are experienced in teaching and computing education research) work together to define the KCs in our scenario.
KCs were defined by two experienced authors with teaching experience in introductory computing courses for at least two semesters in a university setting. In this process, two authors went through all ten problems in the assignment and determined common KCs practiced in the dataset. In the labeling process, two authors first read through the problem requirements and then checked random incorrect submissions from students to determine the KCs practiced. They first summarized the potential KCs as phrases, and collected all KC phrases to determine whether such KCs are kept and discussed. If a potential KC was kept, they went through all problems and labeled the Q-matrix, while using a sentence to define the KC. They also defined two standards to select KCs that cover a range of problems. The first standard to defining a KC is that a KC should be practiced quite frequently in the dataset. If a KC is only practiced in one or two problems, then it might be a KC that is not fundamental to the assignment, making it difficult to model accurately, and not as useful. They also had a standard that a KC cannot be practiced in every problem. If a KC was practiced in all problems, such as exercising the correct syntax in Java, they considered this part of the general challenge programming, which was not our goal to model. They targeted KCs that are practiced in at least three problems and no more than eight problems to follow the two standards. There may be more KCs practiced in the dataset, but they mainly focus on the KCs fitting these two standards. Because our goal for this KC identification process was to reach consensus, rather than to create a standard that each expert could carry out individually, experts worked together synchronously, and they did not attempt to measure inter-rater reliability. Any conflicts, for example when the experts identified different KCs or defined KCs differently, were resolved as they emerged as follows: If a KC was only identified by one of the experts, they discussed to determine if it is a focused KC (meeting the criteria) in the assignment, and worked together to create a definition for it. If a KC was defined differently by the two experts, they resolved the difference by a discussion using examples from student submissions.
The three KCs they defined in the first assignments are:
Between: Construct a boolean expression to determine if a variable is between (two) constants. Examples of the KC is shown in the first column of Figure 2, where the correct constraint is \(10 \leq age \leq 20\) in the correct code, but incorrectly practiced as \(10 < age < 20\) in the incorrect code.N WaySequential Conditions: Order if-statements to reflect mutually exclusive outcomes based on a problem prompt. Example submissions practicing this KC can be found in the second column of Figure 2. In the correct code, when the firstifcondition is met, thecondition Bshould be executed. However, in the incorrect code, thecondition Cis executed in this situation.2xN: Interacting Conditions: Nested if-statements (or create complex expressions in non-nested if-statements) to reflect outcomes at the intersection of two decisions. The examples of this KC are shown in the third column of Figure 2. In the incorrect code, the conditions of the inner if-statement are inversed from the correct code, causing incorrect logic and the incorrect application of this KC.
3.2. Model Design
3.2.1. Supervised Learning
Our goal is to train a model to achieve a supervised learning task: KC attribution (to determine which KCs the student applied correctly and which they applied incorrectly). We define the supervised learning version of the task as follows: Given an incorrect attempt at a problem, and a relevant KC for that problem, determine whether the KC was applied correctly (1) or incorrectly (0). While our goal is to identify all KCs that can be attributed for the incorrect results, we can apply models trained to attribute all relevant KCs get the full list of correctly and incorrectly applied KCs.
3.2.2. Code2vec Model
We use code2vec for solving the KC attribution task. The model code2vec is introduced in Alon et al. (2019) to embed programming code into vectors and use them for tasks such as code classification. Similar to our prior works (Shi et al., 2021, Mao et al., 2021), in this paper, code2vec is used as a base model for the purpose of code embedding. The structure of code2vec is shown in Figure 3. While many more potential code embedding approaches such as CodeBERT (Feng et al., 2020) could be used instead, there are two main reasons why we select code2vec in this work. 1) It has recently been used as the model for investigation in several prior works besides our own work (Fein et al., 2022, Cleuziou and Flouvat, 2021). 2) It represents a category of methods that emphasizes the structural information from programming code through the representations of the abstract syntax tree (AST; see Alon et al. (2018)). By contrast, CodeBERT embeds code at the token level, which loses this syntactic structure. Additionally, pretrained models, such as CodeBERT, are pretrained on massive industrial datasets, which differ meaningfully from our educational context. For simplicity, we therefore focus only on code2vec in this paper, but further studies could compare alternative models to explore language models’ impact on educational tasks, such as KC attribution.
Code Path Extraction: The code2vec model takes students’ code submissions as input,
and they are processed into the \(\mathbf {z}\) vectors to embed the information from students’ code.
Students’ code can be represented in abstract syntax trees (ASTs) as shown in Figure 4.
Students have simple code submissions, the pseudocode is represented as an AST, and the
code2vec model leverages paths as input. For example, the red-labeled path is represented
as
\[\texttt {input|method|body|doSomething|input}.\]
There are three such paths in the simple pseudocode, while in an actual student code submission, there
are much more. Each code path is indexed as three numbers according to two vocabularies.
Two vocabularies are extracted from training datasets. All leaf nodes are represented in a
dictionary \(\mathcal {D}_n\), and all paths are represented in a dictionary \(\mathcal {D}_p\). If the red-labeled path is the \(i\)-th
code path in the submission, it is represented as a three-number index \(b_i = \{s_i, p_i, e_i\}\) as the input for the
code2vec model specified in Figure 3, where \(s_i\) denotes the starting leaf node index, \(p_i\) denotes the
path node index, while \(e_i\) denotes the ending node index. In the red-labeled path of Figure 4,
nodes input are indexed into numbers according to the index of input in \(\mathcal {D}_n\), while the path
“input|method|body|doSomething|input” is indexed into another number according to its
index in \(\mathcal {D}_p\).
Code Path Embedding: A code submission can be represented as multiple code paths. If it has in total \(r\) paths, each path \(i\) is represented as a triplet \((s_i, p_i, e_i)\) and processed by embedding layers \(W_{enode}\) and \(W_{epath}\). Leaf node indices \(s_i\) and \(e_i\) are embedded as \(\mathbf {e}_{s,i} \in \mathbb {R}^{c_n}\) and \(\mathbf {e}_{e,i} \in \mathbb {R}^{c_n}\), and path indices \(p_i\) are embedded as \(\mathbf {e}_{p,i} \in \mathbb {R}^{c_p}\). The dimensions of the embedding matrices are defined by hyper-parameters and the length of dictionaries. The node embedding layer \(W_{enode}\) has a dimension \((l_n+2, c_n)\), where \(l_n\) denotes the length of leaf node dictionary \(\mathcal {D}_n\), and \(c_n\) denotes a hyperparameter of the embedded dimension for nodes, and similarly the path embedding layer \(W_{epath}\) has a dimension \((l_p+2, c_p)\). The extra two rows of both embedding layers represent two additional scenarios of nodes and paths. As padding is needed in our models due to unequal numbers of paths, we assign a row to embed paddings in both embedding layers. As the dictionaries are derived from the training dataset and may encounter unknown nodes and paths in validation or testing datasets, we assign a row to account for unknown nodes and paths in both embedding layers.
Attention Mechanism (Xu et al., 2015): Nodes and paths are embedded into vectors, and for each code path indexed as \(i\), the representation is a triplet \((\mathbf {e}_{s,i}, \mathbf {e}_{p,i}, \mathbf {e}_{e,i})\), concatenated as a vector \(\mathbf {e}_{i} \in \mathbb {R}^{2c_n+c_p}\). The vectors then go through an attention mechanism to calculate the final vectorial representation \(\mathbf {z} \in \mathbb {R}^{2c_n+c_p}\) of the code submission. The attention mechanism has two parts, the weight calculation and the weighted average. In the weight calculation process, every code path embeddings are stacked as a two-dimentional vector \(\mathbf {E} \in \mathbb {R}^{[r, (2c_n+c_p)]}\). The vector then passes through an attention layer \(\mathbf {W}_a \in \mathbb {R}^{[(2c_n+c_p), 1]}\) to calculate a set of weight values \(\mathbf {a}\): \begin {equation} \mathbf {a} = \mathbf {E}\mathbf {W}_a. \end {equation} The vector \(\mathbf {a}\) has \(r\) elements, and every element refers to the importance of the corresponding path. For calculating the weighted sum of vectors, the weight values are normalized to a 1-sum vector through SoftMax: \begin {equation} \bm {\alpha } = \frac {e^\mathbf {a}}{\sum _{i=1}^{{r}}e^{a_i}}. \end {equation} The weight vector \(\bm {\alpha }\) is used to calculate the weighted average for \(\mathbf {E}\) through a dot product operator for the calculation of \(\mathbf {z}\): \begin {equation} \mathbf {z} =\bm {\alpha }^T\mathbf {E}. \end {equation}
In our paper, we use the \(\mathbf {z}\) vectors to represent a code submission, processed by the next functional layers for the KC attribution task. The loss function it optimizes on in the training phase is: \begin {equation} \label {eq:lbase} \mathcal {L}_{base} = CrossEntropy(\bm {y}_a,\hat {\bm {y}}_a). \end {equation} In the equation, the loss \(\mathcal {L}_{base}\) is the CrossEntropy (De Boer et al., 2005) of the expected KC attribution label (\(\hat {\bm {y}}_a)\)) and model output (\(\bm {y}_a\)), where positive (1) means the KC is correctly applied in the submission. The model is trained and tested on labeled KC attribution data, as we mentioned the labeling process in Section 4.3. This is a traditional supervised learning approach, and it addresses research question (RQ1) about how well deep learning will solve the KC attribution task with different sizes of training data. Our expectation for code2vec is that code2vec will perform better than traditional machine learning methods such as SVM and logistic regression, as it has been better in other educational tasks (e.g., Shi et al. (2021), Shi et al. (2022)).
3.2.3. Transfer Learning
As we have only limited access to labeled data for the supervised learning task of KC attribution, we need a method that leverages less labeled information but still works for the KC attribution task. We use the transfer learning method (Torrey and Shavlik, 2010) in this paper and evaluate how this method compares with the supervised learning method. Transfer learning is a strategy in which we have a model trained in one task (Task A) and have the model applied to another task (Task B), and one hypothesis is that the information learned in Task A can be used directly in Task B (Torrey and Shavlik, 2010). The task of KC attribution fits well along this hypothesis: We have an abundance of labels about whether a submission is correct or not, and the automated grading is achieved by automatic grading tools such as test cases (e.g., Wick et al. (2005)). Our hypothesis in this paper is that if we train a model from this information, it can be applied for the KC attribution task. We define the task we train the model on as the KC relevance detection task: Given a student’s correct attempt at a problem, determine whether a given KC is relevant (1) or not relevant (0) to that problem. Solving this problem is of less value by itself, as it is not hard to manually label relevant KCs for a problem. However, we hypothesize that solving it will transfer to the KC attribution task. We make the simplifying assumption that a problem has a fixed set of KCs, which are always relevant and present in all students’ solutions. This generally holds for our problem set but may not hold in all situations. To facilitate the setting of transfer learning, we set up the experiments as indicated in Figure 5. The model is trained and tested on labeled correctness data of the submissions. This model is used for the evaluation of transfer learning performance for the KC attribution task (RQ2). We won’t expect that the transfer model will perform as good as the supervised model, but this method requires no manual labeling, and we hypothesize that the transfer model works well in certain cases where transfer learning may work. To evaluate whether the KC relevance detection task could benefit the supervised learning task, we combined the two tasks in the model. We created a multi-task model to evaluate if the performance of KC attribution can further improve.
3.2.4. Multi-Task Model Design
We further explored whether the KC relevance task could be designed to serve as a component in the supervised model training, merging the two tasks in one multi-task model. The design is shown in Figure 6. The model combines KC relevance detection and KC attribution using two branches in the training process. When input belongs to a group (relevance or attribution), the model calculates only one branch. For example, when the input is a correct submission, only KC relevance loss is calculated for optimization, while when a labeled incorrect submission is the input, the KC attribution loss will be calculated. More specifically, when the input is a correct submission, we calculate the loss function as \begin {equation} \mathcal {L}_{multitask} = CrossEntropy(\bm {y}_r,\hat {\bm {y}}_r), \end {equation} and when the submission is incorrect but relevant to the KC we detect, the loss function is \begin {equation} \mathcal {L}_{multitask} = CrossEntropy(\bm {y}_a,\hat {\bm {y}}_a), \end {equation} where \(\bm {y}_r\), and \(\hat {\bm {y}}_r\) represent the detected value and ground truth, respectively, for KC relevance. In the training process, we do not include any samples from students in the testing or validation splits, even though the correct submissions from these students are not evaluated in the validation or testing phases. More details of data usage schema can be found in Section 4.4. We hypothesize that if the simple combination of the two tasks in the multi-task model improves the performance of supervised learning, the submission correctness labels extend the information learned by the model beyond what it can learn from the KC attribution labels. However, if it does not perform better than supervised learning, it may indicate that the information contained in submission correctness labels is a subset of information in KC attribution labels when we train a model for the KC attribution task. This helps us further understand how transfer learning works, what information can be transferred, and whether the submission correctness labels offer more information.
3.2.5. Learning Curve Integrated Model Design
As introduced in Cen et al. (2006), the practice of KCs from a group of students should follow the power law of practice (Snoddy, 1926), namely their error rate \(Y\) on a KC when practicing relevant problems start at a rate \(a\) and drop at an exponential rate \(b\) with the increase of practice opportunities \(X\), as specified in Section 2.1. In our work, we assume that students experience the exponential learning curve on both manually defined KCs and discovered KCs. The learning curve theory is known as the basis of many methods (Cen et al., 2006, Pavlik et al., 2009, Chi et al., 2011) in KC refinement tasks. Under this theory, we have the \(a\) and \(b\) parameters fixed at an assumed value in the attribution of KCs, since such parameters cannot be inferred before we know the actual students’ demonstration of KCs on each step. We expect the learning curve could improve the performance of KC attribution due to the theoretical support from the literature. However, it may also not work because students’ work may not adhere to learning curves. For example, when the model output is close to \(0.5\) without a learning curve constraint, it means that the model does not have a strong attribution. Having the ideal learning curve to yield an output closer to the expected error rate makes the attribution fit better to theory. It is worth noting that incorporating learning curves may or may not provide a great direction to optimize, since our expert labels (as introduced in Section 4.3) do not yield perfect learning curves. In our experiments, we explore, in the best scenario, how much improvement the learning curves can bring to the models, and we inferred the best \(a\) and \(b\) parameters from the labeled data using non-linear least squares methods (Moré et al., 1980) to fit the exponential curve.
The learning curve incorporated transfer model structure is shown in Figure 7. It has two parts following the code2vec model introduced in Figure 3 in the training process for loss calculation and optimization. In the training process of the transfer learning scenario, learning curves further augment the code2vec model. In the inference process, the trained model is used to attribute KC and the results are evaluated on the labeled data. The loss \(\mathcal {L}_{lc}\) is calculated as: \begin {equation} \label {eq:lc} \mathcal {L}_{lc} = \alpha \mathcal {L}_{base} + (1-\alpha )\frac {1}{T}\sum _{T} |c_{t} - \hat {c}_{t}|. \end {equation} In this equation, we denote the learning curve value of the KC we focus on a submission \(t\) as \(c_{t}\), and in total, there are \(T\) submissions that are expected to practice the KC. As introduced in Equation 4, \(\mathcal {L}_{base}\) indicates the loss value of the base model, and \(\alpha \) is a factor controlling the weight of learning curves calculated in the process. Another important part of the equation \(\hat {c}_{t}\) refers to the expected error rate of the batch of students on the \(t\)-th submission. It is calculated using the power law of practice as introduced in Section 2.1. It has two assigned parameters: the learning rate \(b\) and the starting error rate \(a\). The value of the detected KC error rate is calculated as the mean of attribution \(k_{n,t}\) at submission \(t\) for student \(n\) in this KC using an equation: \begin {equation} c_{t} = \frac {1}{N}\sum _N k_{n,t}, \end {equation} where \(N\) refers to the batch size of students in optimization. Since we aim to examine whether ideal learning curves would help model training, we extracted the \(a\) and \(b\) values in all three KCs using our labeled data.
3.2.6. Baseline Models
We leveraged baseline models to evaluate and compare the performance of deep learning-based models as our work builds upon the optimization of deep neural networks. The baseline models are created for both supervised learning and transfer learning scenarios to make comparisons and show whether deep learning methods work better in either/both scenarios. As introduced in Section 3.2.2, we processed students’ programming code into code paths as the input of the code2vec model. However, for baseline models, such processing does not directly apply. In this paper, we compare our results with two commonly used baseline models (as used in Marwan et al. (2021) and Gervet et al. (2020)): logistic regression (LR) and support vector machine (SVM). Students’ code are processed by the TF-IDF method for both baseline models, which extracts the frequency of terms showing up in students’ code. LR and SVM methods use the frequency features to detect the correctness of KCs, serving as baseline models to compare with the other models we proposed in the paper. The comparisons of baseline models help us understand the roles of deep learning in solving the KC attribution task. With the comparison, we will understand how much advancement a deep learning model could bring over traditional machine learning methods. We further explore whether the differences apply in supervised learning scenarios and transfer learning using the comparisons with baseline models. There are many advanced models such as Feng et al. (2020) that could also serve as baseline models, which we save as future work.
4. Experiment
4.1. Dataset
We use the publicly available CodeWorkout dataset2 for our experiments. The dataset is collected in Spring 2019 from Virginia Tech in an introductory Java Course (CS1 Java), and contains five assignments as practices for students to write code and practice their skills learned in classes. The dataset contains submissions from 410 students, averaging 10 to 20 lines of code. It is stored in ProgSnap2 (Price et al., 2020) format, and geographical information has been unidentified for ethical considerations. In each of the five assignments, students write code in the CodeWorkout platform (Edwards and Murali, 2017) to solve ten problems and submit their finished code to the system to check the correctness. We selected the first assignment as our data source. As introduced in Section 3.1, three KCs are tagged from \(48\) students in the dataset. Among all submissions in the first assignment, \(26.14\%\) of code submissions pass all test cases and are labeled as correct.3
4.2. Data Processing
We followed similar data processing steps introduced in Shi et al. (2023), as this work also used the CodeWorkout dataset. Processing the students’ code submissions involves two key steps: labeling the first submissions and filtering potential cheating students.
The step of labeling first submissions from students is different from the Shi et al. (2023) paper. In our scenario, both the first and non-first submissions are needed for both the training and validation processes, and keeping both submissions have been the setting by other previous work (e.g., Rivers et al. (2016)). Marking first submissions are necessary for the application of learning curves in the model, and the calculation of learning curves should only involve the first submissions from students.
We further observed several potential cheating students in the dataset. For example, some students struggled early in the course, barely finishing the first easier problems with less than ten attempts, but after a certain time, they achieved the goals of problems with their first try in much more difficult problems. We reduced the risk of including cheating students’ data in a student model and used some preliminary effort to exclude potential cheating students. Without evidenced methods available, we follow previous work in Shi et al. (2023) to use a threshold and exclude students with submission traces struggling first and achieving all more difficult problems later.
4.3. KC Labeling
After defining the KCs, we sampled 48 students to label their incorrect submissions and attribute their errors to the KCs we defined for each assignment. Specifically, the 48 students were divided into two groups: 10 and 38. Two authors independently labeled the 10 students’ submissions and merged them to see potential inconsistencies and look for updates in the definitions in the first round. In the first round of labeling, the two authors checked the KCs labeled and found that the labeling were consistent with Cohen’s Kappa value of \(76.46\%\), reaching excellent agreement (Fleiss et al., 2013). Then after discussing to resolve the conflicts, one author labeled all the remaining 38 students’ incorrect submissions. This labeled dataset will be later released as a benchmark for future research.
We plotted the learning curves from the 48 labeled students for the KCs defined in the first assignment, shown in Figure 8.
Between, N Way, and 2xN.
4.4. Training, Validation, and Testing Scheme
The detailed schedule of data usage can be seen in Figure 9. All students’ data are split into two subsets: one set with 48 students which we label the KC attributions, and another set we don’t have the KC attributions. To tune the hyperparameters, we performed 5-fold cross-validation on splits of students. We performed the hyperparameter grid search on training epochs (20 through 200) and learning rates (1e-5 through 1e-3), and the averaged AUC values across folds are used to determine the hyperparameters of the models.
In the scenario of supervised learning, as shown in Figure 9, we performed nested cross-validation. The supervised learning model is trained, validated, and tested by labeled KC attribution data. The outer layer of cross-validation is for the train test split, and we perform this layer of cross-validation to report the stable testing result averaging from the five folds. Inside each training-validation run, we perform another layer of 5-fold cross-validation to determine the hyperparameter that achieves the best results.
In the transfer learning scenario, the model is trained on the KC relevance detection task on the unlabeled dataset for the KC attribution task. Compared with the supervised learning task, the outer layer of cross-validation is replaced by ten times repeated runs to report stable results. In the 10-fold cross-validation hyperparameter selection process, we made early stops when the results reached 95% AUC and continued growing when we changed the hyperparameter to more complex models. We made the threshold choice since the high performance on the KC relevance detention task does not reflect a high performance on the KC attribution task, as the testing is on the KC attribution labels of incorrect submissions. Too high performance with better than 95% AUC on the KC relevance detection task makes little contribution to the KC attribution task.
The multi-task model (introduced in Section 3.2.4) has a similar setting with supervised learning, and the difference is that besides the labeled data used for training, the multi-task model leverages unlabeled samples, and the model is trained with a mixture of labeled and unlabeled data points on the task of KC attribution, as it achieves learning of two tasks, KC relevance detection and KC attribution at the same time.
For the other baseline models, both models used the same parameter searching process, with 10-fold cross-validation, to find the best performance in the validation dataset, and results are evaluated on the testing dataset.
5. Results
5.1. Supervised KC Attribution
In this subsection, we aim to answer RQ1: How do deep learning methods that analyze students’ code perform on the KC attribution problem, how does this compare to traditional models, and how does this performance vary with the amount of data available?
We examined the performance of code2vec and other traditional models in the task of KC
attribution using supervised learning scheme mentioned in Section 4.4. The results are shown in
Table 1. As the table suggests, KC attribution using students’ code is a difficult problem to solve.
Baseline models using standard TF-IDF do not achieve AUC values above 0.5, meaning all baseline
models are worse than chance. This reinforces what prior work has suggested about the challenges of
understanding student code. Despite the challenge, a deep learning model is still making
meaningful predictions using supervised learning. It outperforms the baselines on AUC by
0.4-0.1. The AUC values it achieves are all better than chance, and on some KCs, such as
between, are potentially accurate enough to generate useful insights for students, instructors
and researchers. However, performance varies a lot across KCs (though not across runs),
suggesting that this approach may not always produce actionable predictions. We perform
further analysis on scenarios when the supervised code2vec models work and don’t work in
Section 5.4.
| KC | Metrics | SVM | LR | code2vec |
|---|---|---|---|---|
|
Between | AUC | 0.3303 | 0.3611 | 0.8076 (0.0751) +-0.0335 |
| F1 Score | 0.7636 | 0.7857 | 0.8289 (0.0427) +-0.0191 |
|
|
N Way | AUC | 0.2813 | 0.2570 | 0.7680 (0.0988) +-0.0442 |
| F1 Score | 0.6923 | 0.6400 | 0.5910 (0.0813) +-0.0363 |
|
|
2xN | AUC | 0.4564 | 0.4666 | 0.5872 (0.1107) +-0.0495 |
| F1 Score | 0.4545 | 0.4615 | 0.4352 (0.1241) +-0.0555 |
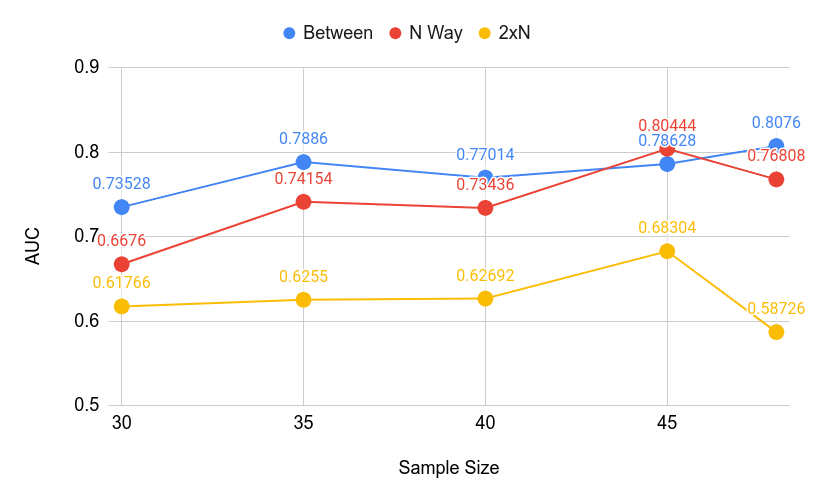
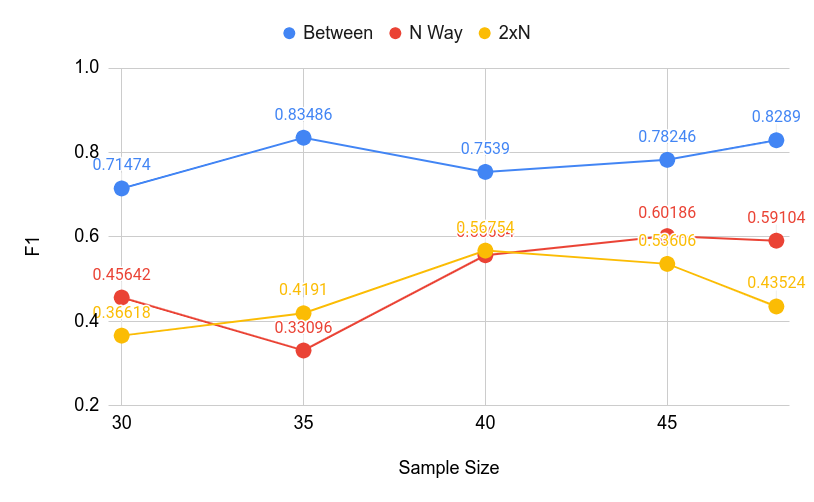
5.1.1. Cold Start Experiment
We also conducted a cold start experiment (like in Shi et al. (2021)) when trained
with limited data to determine the relationship between data size and performance for the supervised
code2vec model. We started from 30 labeled students and incremented by five labeled students in the
training dataset to reach the total 48 labeled students’ data, and visualized the results in
Figures 10 and 11. The cold start curves suggest that while the relationship is not entirely linear, more
data seems to help. While generally, the model performs better when more data is available, the
performance of 2xN and N Way correctness detection dropped with lower AUC and F1 scores when
using full 48 labeled students’ data. A minimum amount of data is necessary for deep models to
converge. When the number of training samples is deficient (e.g., when there are only 15 samples), the
performance achieved by the models is not stable enough to be reported and considered
valid. It also shows that we still need more data labeled to reach more stable results. This
data is very costly to produce; thus, we need to evaluate the second research question in
the next section: When we don’t have labels about KC attribution, could transfer learning
work?
5.2. Transfer KC Attribution
In this subsection, we aim to answer RQ2: To what extent can information learned from other, more readily available labels (i.e., submission correctness) be applied to solving the KC attribution problem?
| KC | Metrics | Transfer SVM | Transfer LR | Transfer code2vec | Transfer code2vec + Learning Curve | Multi-Task code2vec | Supervised code2vec |
|---|---|---|---|---|---|---|---|
|
Between | AUC | 0.4353 | 0.4259 | 0.7169 (0.0480) +-0.0089 | 0.7242 (0.0519) +-0.0096 | 0.7383 (0.0941) +-0.0420 | 0.8076 (0.0751) +-0.0335 |
| F1 Score | 0.7735 | 0.7735 | 0.8008 (0.0148) +-0.0027 | 0.8019 (0.0265) +-0.0049 | 0.7926 (0.0656) +-0.0293 | 0.8289 (0.0427) +-0.0191 |
|
|
N Way | AUC | 0.3553 | 0.4268 | 0.6798 (0.0659) +-0.0122 | 0.6297 (0.0589) +-0.0109 | 0.7865 (0.0609) +-0.0272 | 0.7680 (0.0988) +-0.0442 |
| F1 Score | 0.5517 | 0.5479 | 0.5968 (0.0387) +-0.0027 | 0.5453 (0.0476) +-0.0071 | 0.5848 (0.0658) +-0.0294 | 0.5910 (0.0813) +-0.0363 |
|
|
2xN | AUC | 0.4928 | 0.4228 | 0.5035 (0.0458) +-0.0085 | 0.5704 (0.0470) +-0.0087 | 0.5637 (0.0833) +-0.0372 | 0.5872 (0.1107) +-0.0495 |
| F1 Score | 0.6162 | 0.6162 | 0.6100 (0.0182) +-0.0033 | 0.5906 (0.0269) +-0.0050 | 0.1947 (0.2348) +-0.1050 | 0.4352 (0.1241) +-0.0555 |
The results are reported in Table 5.2. One observation from the table is that the baseline
transfer models perform generally lower than the transfer code2vec models. In all three KCs,
the transfer code2vec model performed better than the transfer support vector machine
(SVM) and logistic regression (LR) models. On the Between and N Way KCs, code2vec
achieves about 25% better in the AUC metric. However, on 2xN correctness detection, the
performance of code2vec is only 1% better than SVM, but all models on 2xN correctness
detection suffer from very low performance with highest performance of 58.72% when the
code2vec model is trained in a non-transfer way. In general, the models perform much better in
detecting the Between KC correctness than detecting the correctness of the other two
KCs.
Another direct observation is that the supervised model performed better than the transfer models, with all AUC scores better than other models, though with lower F1 scores than two KCs. The result shows that although trained with much more unlabeled data (data only with problem correctness information from 362 students), the code2vec model still performs better when trained with limited labeled data (data with KC correctness information from 38 students). The difference between transfer code2vec and the supervised version is smaller than 10% in AUC score, showing that while no information about KC attribution is available, the model learned needed information from the KC relevance labels.
5.2.1. Multi-Task Model Results
As introduced in Section 3.2.4, we also worked on analyzing the performance of the multi-task model. Our results in Table 5.2 show that with the help of KC relevance detection information, the multi-task model performed even lower than the supervised code2vec model, showing that without specific considerations in model design, the information contained in the data used for the KC relevance task does not add much to KC attribution, and is likely a subset of the information contained in the labeled data when training for the task of KC attribution.
5.3. The Effect of Learning Curve Incorporation
We further examined whether learning curve incorporation could further improve the
results of transfer learning, as asked in RQ3. As Table 3 suggests, comparing the results
of transfer code2vec models with or without learning curves, we find that in the task of
detecting the correctness of two of the three KCs, learning curves show the potential of
helping the model to perform better. In the attribution of Between, the learning curve
helped the model to improve by 0.73%, while in the attribution of 2xN, the improvement is
6.69%. However, in the KC N Way, the performance is lower than the transfer model without
incorporating learning curves. Our experiment shows that learning curves could or may not be
helpful for the transfer model in the KC attribution task, depending on the actual KC we work
on.
|
KC |
Metrics | Transfer code2vec | |||||
|---|---|---|---|---|---|---|---|
| \(\alpha =0\) | \(\alpha =0.001\) | \(\alpha =0.00011\) | \(\alpha =0.0001\) | \(\alpha =0.00009\) | \(\alpha =0.00001\) | ||
|
Between | AUC | 0.7169 (0.0480) +-0.0089 | 0.6709 (0.0783) +-0.0145 | 0.7185 (0.0530) +-0.0098 | 0.7242 (0.0519) +-0.0096 | 0.7235 (0.0535) +-0.0099 | 0.7142 (0.0541) +-0.0100 |
| F1 Score | 0.8005 (0.0148) +-0.0027 | 0.7853 (0.0215) +-0.0040 | 0.8016 (0.0258) +-0.0048 | 0.8019 (0.0265) +-0.0049 | 0.8007 (0.0270) +-0.0050 | 0.7988 (0.0166) +-0.0075 |
|
|
N Way | AUC | 0.6798 (0.0659) +-0.0122 | 0.6014 (0.0429) +-0.0079 | 0.6135 (0.0534) +-0.0099 | 0.6297 (0.0589) +-0.0109 | 0.6606 (0.0727) +-0.0135 | 0.6735 (0.0800) +-0.0125 |
| F1 Score | 0.5968 (0.0387) +-0.0027 | 0.5194 (0.0472) +-0.0087 | 0.5412 (0.0523) +-0.0097 | 0.5453 (0.0476) +-0.0071 | 0.5558 (0.0430) +-0.0079 | 0.5997 (0.0404) +-0.0075 |
|
|
2xN | AUC | 0.5035 (0.0458) +-0.0085 | 0.5218 (0.0503) +-0.0093 | 0.5613 (0.0569) +-0.0105 | 0.5704 (0.0470) +-0.0087 | 0.5554 (0.0557) +-0.0103 | 0.5647 (0.0513) +-0.0095 |
| F1 Score | 0.6100 (0.0182) +-0.0033 | 0.5479 (0.0718) +-0.0133 | 0.5913 (0.0348) +-0.0064 | 0.5906 (0.0269) +-0.0050 | 0.5824 (0.0339) +-0.0062 | 0.6211 (0.0228) +-0.0042 |
|
In Section 3.2.5, we introduced that the learning curve has been incorporated to the code2vec
model using an \(\alpha \) parameter to control the weight in the loss function. To further evaluate when learning
curves perform better for the three KCs, we ran multiple runs using different weights on learning curve
losses. We changed the value of \(\alpha \) (see Section 3.2.5) to control the portion of loss coming
from the learning curve and KC existence label cross-entropy. We tested the \(\alpha \) values in a
range of \(1e-3\) to \(1e-5\) as larger values yield results that overly fit to the learning curves. Our results
are shown in Table 3, which shows results for various alpha values. When \(\alpha = 0\), the model is
equivalent to the Transfer code2vec model in Table 5.2. The model performance seems
best overall when \(\alpha \) is assigned as \(0.0001\). In detecting the KC Between, we found that adding
learning curves did not bring big performance improvements across all \(\alpha \) values. For the
detection of KC N Way, the incorporation of learning curves did not improve the performance,
with the best performance achieved by no learning curve weight involved and the second
best performance achieved by our lowest \(\alpha \) value attempted. The detection of KC 2xN was
improved by incorporating a learning curve loss function. While the changes of \(\alpha \) values make
bigger differences than the other two KCs, the presence of learning curves helped across all
scenarios compared with no learning curve involved. Our results show that in the base cases,
learning curves may or may not be used as an additional source of information to enhance
the performance of KC attribution transfer models, and it depends on a good selection of \(\alpha \)
values.
5.4. Case Studies: When Will Transfer Work?
The quantitative data clearly shows that the transfer model performs better than chance, and is clearly picking up on relevant features, and we use examples to illustrate why and how this may have been possible. We show several cases when transfer models work and don’t work and the impact of including learning curves on the model training process in this section. For each of the cases, we train and run the model ten times and report the average detected probability of students achieving the KC, compared across the transfer model, the learning curve improved transfer model, and the supervised model. In all cases, detection values \(\geq 0.5\) suggest a detection of the KC is correctly practiced.
5.4.1. Case A: Transfer Learning on Non-Existing KC
| Code | KC | Transfer Attribution | Learning Curve Transfer Attribution | Supervised Attribution |
|---|---|---|---|---|
|
} } } | Between | 0.1278 | 0.0777 | 0.3159 |
Problem Description: Write a function in Java that implements the following logic: Given 2 ints, a and b, return their sum. However, sums in the range 10..19 inclusive, are forbidden, so in that case just return 20.
As shown in Table 4, the goal of the code is to return a number, either 20 or the sum of the two
inputs. It is determined by the if condition. The condition implemented in the code is that either the sum
of the two inputs equals to 10 or 19. However, it does not satisfy the requirement of the problem, which
requires a range to be implemented. Since the implementation of range does not exist, the
practice of the KC between is incorrect. Thus, since the transfer model is trained on the KC
relevance detection task, it is able to detect that the KC is not practiced, which is a correct
detection for the task of KC attribution. Besides the transfer model, the learning curve improved
transfer model and the non-transfer model both make correct predictions as well on this
submission.
5.4.2. Case B: Learning Curve Improved Correctness Detection
| Code | KC | Transfer Attribution | Learning Curve Transfer Attribution | Supervised Attribution |
|---|---|---|---|---|
|
} } | N Way | 0.9942 | 0.4448 | 0.4000 |
Problem Description: You and your date are trying to get a table at a restaurant. The parameter you is the stylishness of your clothes, in the range 0..10, and date is the stylishness of your date’s clothes. Write a method that returns your chances of getting a table, encoded as an int value with 0 = no, 1 = maybe, 2 = yes. If either of you is very stylish, 8 or more, then the result is 2 (yes). With the exception that if either of you has style of 2 or less, then the result is 0 (no). Otherwise the result is 1 (maybe).
In Table 5, we show a case that the transfer model fails to attribute the KC N Way, but the
incorporation of learning curves helps the model make the correct attribution. The code is intended to
solve a problem of parallel conditions, practicing the KC N Way. From the code, we can see the KC
has been practiced, although in a nested way. The issue of the submission is that when the
input has a number smaller than integer 8 and another number smaller or equal to integer
2, the output will be integer 1. However, it is supposed to return an integer 0. It has been
unique for this problem across the dataset, and the KC can be incorrectly applied only this
way in this problem. However, the transfer model cannot learn the information from other
problems. The transfer model detects the relevance of the KC N Way and returns that the
KC is correctly practiced, while the non-transfer model successfully detects that the KC is
practiced incorrectly, returning that the KC is incorrectly practiced. The incorporation of
learning curves helped the model to drop the probability of the KC correctness to make it
closer to the expected value in the ideal learning curve, since the problem is one of the
relatively early problems practiced in the dataset. In general, students are less likely to practice
it correctly, and thus, with the help of learning curves, the average detected probability
of KC correctness has been dropped to less than \(0.5\), leading to an accurate detection. It is
also worth noting that it could be misleading in other cases since the learning curve is not
personalized to the student, simply taking the number of prior relevant practices on the
KC.
5.4.3. Case C: Limitations of Supervised code2vec
| Code | KC | Transfer Attribution | Learning Curve Transfer Attribution | Supervised Attribution |
|---|---|---|---|---|
|
} | 2xN | 0.6754 | 0.5599 | 0.3712 |
Problem Description: When squirrels get together for a party, they like to have cigars. A squirrel party is successful when the number of cigars is between 40 and 60, inclusive. Unless it is the weekend, in which case there is no upper bound on the number of cigars. Return true if the party with the given values is successful, or false otherwise.
While the supervised model successfully detected the correctness of the KCs in the previous two
cases, it may fail in certain cases. We show an example of a failure from the supervised model in
Table 6. The students’ code is incorrect only due to a typographical error in the number of if
conditions. It could be seen as an incorrectly practiced KC Between, but the practice of KC 2xN is
successful. While both transfer models accurately attributed the KC 2xN, the supervised model failed
to make the detection. One primary reason might be the limited training dataset of the supervised
model, and such a typographical error may not have been available in the training dataset, leading to an
incorrect model result.
The above three case studies show how the transfer learning and learning curves help in the task of KC attribution. While they only represent a single case presented in the dataset, we hope to use the cases to raise plausible explanations for why we saw the results earlier. These cases show that the transfer model learns the information of KC relevance, which is likely a subset of information of KC attribution. If a KC is supposed to be practiced but not even present, it cannot be correctly practiced. While the transfer model does not have any information about correctly practiced KCs, the incorporation of learning curves introduces another source of information – from an angle of educational theory to generally regulate the results depending on the number of questions students already practiced for the KC. We also show that in certain cases, supervised models could fail on the task of KC attribution simply due to the lack of labeled data points, which is one reason why we apply transfer learning methods.
6. Discussion
6.1. Research Question 1: KC Attribution with Deep Learning Method
Our results indicate that it is possible to solve the KC attribution problem in programming using expert-defined KCs, rather than using syntax tokens as KCs as in prior work (Hosseini and Brusilovsky, 2013, Rivers et al., 2016). This approach presents a number of advantages (e.g., clear human interpretability, ability to align with educational theory and curriculum design, etc.). Our results show that using expert-defined KCs, the problem is tractable but challenging, with our best-performing model achieving about \(80\%\) AUC scores in the KCs. We also found that the learning curves from our expert-labeled KCs were not unreasonable but were far from ideal. This is likely due to the granularity of KCs we focused on (e.g., omitting KCs that were present across all problems or only on one problem), and the general challenge of building learning curves for multi-KC problems. Another implication is that the code-specific deep learning models clearly outperform traditional text feature extraction approaches, adding to prior literature on the advantage of domain-specific models for student modeling (Shi et al., 2021, Shi et al., 2021). From the relatively low performance of the supervised learning, we found that data labeling is necessary for any supervised learning approach, although time-consuming and challenging. Results from the cold start analysis also show the necessity of a minimum labeled dataset size and the potential gains of labeling more data.
6.2. Research Question 2: KC Attribution with Limited Data
Our experiments with transfer learning and multi-task models have further implications. The results
indicate that some information transfers from the KC relevance problem to the KC attribution problem.
These are two very different problems with two very different datasets. One contains only correct
solutions, and we’re trying to transfer to incorrect submissions. The result shows the potential of
transfer learning in this context. We also found that transfer learning works on some KCs, but it may
also not work without further improvement on other KCs (e.g., N Way). The multi-task
model results show that the information learned from the KC relevance problem is largely
redundant with the information learned from the KC attribution problem. When using a
multitask learning approach, our results show that combining information learned from
these tasks does not lead to meaningful improvement over the basic supervised learning
approach.
6.3. Research Question 3: Learning Curve Incorporation
Our experiments on incorporating learning curves have further implications as well. The results show that aligning KC attribution predictions to learning curves helps predictions in some cases, harms them in others, and has little effect overall. The results are achieved using hard-coded hyperparameters of the ideal learning curves, extracted from labeled KC attribution dataset, but still, the results show that the integration of learning curves is not very effective for improvements in performance. Given that our expert-labeled KCs did not produce particularly power-law-aligned learning curves, it is not surprising to find limited improvement in the incorporation of ideal or expected learning curves.
6.4. Teaching and Research Implications
There are many ways to use this KC attribution model in practical computing education. The KC attribution method can directly be leveraged to provide formative feedback (Shute, 2008) to students. Since the method indicates the incorrectly practiced KCs, students can refer to this information to correct their understanding of certain knowledge they practiced. The work will also benefit teachers in understanding students’ understanding of KCs in general as summative feedback with statistical analysis of the model results. For example, without extensive effort, teachers can send the new batch of student submissions to a trained model and generate a distribution of students’ correctness on KCs they have taught and required students to practice on. Such information can be used to improve their pedagogical design and choices further. Furthermore, our work can be an initial step for personalized learning. When we receive confirmed and repeated incorrect submissions on certain KCs from a student, automated interventions such as relevant problems can be recommended to students and let them further improve. Our work can serve as the supporting algorithm behind an interface for instructors and students to improve learning experiences.
Our work also contributes to student modeling tasks. It is worth noting that KC attribution is not the same as knowledge tracing, but it could improve knowledge tracing. Currently, knowledge tracing models in programming (Shi et al., 2022) make predictions about which problems will be right but not which KCs the students have mastered. Using KC attribution as input to knowledge tracing could allow it to predict the KC level more accurately. Additionally, in a lot of publicly available and especially large datasets (Pandey and Srivastava, 2020, Zhang et al., 2017, Schmucker et al., 2022, Huang et al., 2023, Shen et al., 2021, Yang et al., 2020), they only include true or false, multiple choice, or short answer questions. Such questions often only require students’ mastery of a small number of KCs, and they don’t have the information directly showing the steps students take to solve the questions. In our scenario, we have the information about students’ actual programs and thus leveraged them to pursue further the knowledge-level detection and profiling with designed feature extraction methods stemming from code2vec (Alon et al., 2018, Alon et al., 2019). Our work provides a direct detection of students’ knowledge by applying deep data-driven models.
6.5. Caveats and Future Work
Our work has several limitations to consider when applied to broader contexts. One important limitation is that our results are based on a small set of population with more than 300 students. We only used students’ submissions on one assignment, although it is a core topic in CS1 courses. Further work can further explore an expansion of population, assignments, and courses. Our method is currently based on the code2vec model, while many more possible deep learning models, such as CodeBert (Feng et al., 2020), could also serve as the base model and may get different results. We use this research as an example to show that the code2vec model can achieve low-label detection in a relatively usable performance, and transfer learning could be an alternative method when no labels are available. While the experiments show that on two of the KCs we can achieve AUC scores higher than 75%, it is still relatively low, and the reliability of the model when deployed in classrooms will need further improvement. We also have some internal experimental caveats in the paper. For example, the labeling process only involved two authors extensively, while the KC attribution and definitions may need rigorous cognitive task analysis (Clark et al., 2008). KC, by the definition of the Knowledge-Learning-Instruction (KLI) framework (Koedinger et al., 2012), should not be directly observable as a cognitive process of the human brain. In our KC attribution project, this detection refers to the KCs practiced in the submissions since our goal is to explore the possibility of detecting KCs demonstrated in the problems, which caused our choice of labeling from the dataset. One of our contributions is that we explored the impact of learning curves on the performance of the models. This contribution aims to explore the best scenario of such incorporation with ideal learning curves and is based on the assumption that the \(a\) and \(b\) parameters are known from the testing population. While in practice, this won’t be true, our results show that given an estimate of the parameters, in best scenarios, the learning curves do not benefit the performance by much. While learning curves do not help much for the KC attribution task, as we show in our experiments for the dataset, it may still be worth trying in other datasets or domains. Our work is still relatively early, and many more are to be done along this line of research.
In the future, we envision three directions as extensions of the work. We will continue to work on more datasets collected in different courses with different populations, and work on other assignments. Since our results were limited to the CodeWorkout dataset, replication studies on more datasets are important to confirm the generalizability of our results, and we plan to explore different scenarios and evaluate if they are consistent. As we mentioned in Section 3.2.2, this work only investigates the performance of a single deep learning model, code2vec, on the KC attribution task, and many more base models (e.g., CodeBERT (Feng et al., 2020), code2seq (Alon et al., 2019)) could also be implemented in future study to explore how different base models achieve the KC attribution task. Our second direction is to create tools based on such detections to evaluate if the detector-based interventions can benefit students’ learning. Further research can create prototype interfaces to return feedback to students and use tests, surveys, and interviews to investigate students’ learning gain with the help of more pinpoint feedback for students, as well as potential affect measures such as engagement in the class. Finally, one potential direction is to compare the currently available large language models on KC attribution. While LLMs offer off-the-shelf detection and are usually trained under huge amounts of information, their performance may not be better than our specifically designed models. Further investigations on leveraging the information from LLMs in our models could also bring further improvements as a future study.
7. Conclusion
In this paper, we introduce a knowledge component (KC) attribution method using students’ program submissions in a CS1 Java course. Our results show that the code2vec model is able to use a small amount of labeled data to achieve higher than 75% AUC scores in two of the three KCs we work on, and using transfer learning, we can train a model from KC relevance labels and achieve comparable performance to the supervised code2vec model. Our experiments on learning curves further show that they hold the potential to improve further the performance of KC attribution on transfer models, but our extensive experiments did not return results improved by much with the help of ideal learning curves. Our work can be one of the stepping stones of future research in personalized interventions, such as providing formative feedback to students, as well as student knowledge profiling tasks to gain more understanding of their knowledge status.
Acknowledgement
This material is based upon work supported by NSF under Grant No. #2013502 and #2112635, and the Goodnight Educational Foundation.
Editorial Statement
Min Chi had no involvement with the journal’s handling of this article in order to avoid a conflict with her Associate Editor role. The entire review process was managed by Special Guest Editor Maria Mercedes T. Rodrigo and Journal Editor Agathe Merceron.
References
- Ai, F., Chen, Y., Guo, Y., Zhao, Y., Wang, Z., Fu, G., and Wang, G. 2019. Concept-aware deep knowledge tracing and exercise recommendation in an online learning system. In Proceedings of the 12th International Conference on Educational Data Mining (EDM 2019), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, 240–245.
- Aleven, V. and Koedinger, K. R. 2013. Knowledge component (kc) approaches to learner modeling. In Design Recommendations for Intelligent Tutoring Systems, R. A. Sottilare, A. Graesser, X. Hu, and H. Holden, Eds. Vol. 1. US Army Research Laboratory, Chapter 15, 165–182.
- Allamanis, M., Peng, H., and Sutton, C. 2016. A convolutional attention network for extreme summarization of source code. In Proceedings of The 33rd International Conference on Machine Learning, M. F. Balcan and K. Q. Weinberger, Eds. PMLR, 2091–2100.
- Alon, U., Brody, S., Levy, O., and Yahav, E. 2019. code2seq: Generating sequences from structured representations of code. In International Conference on Learning Representations.
- Alon, U., Zilberstein, M., Levy, O., and Yahav, E. 2018. A general path-based representation for predicting program properties. In Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, D. Grossman, Ed. Association for Computing Machinery, 404–419.
- Alon, U., Zilberstein, M., Levy, O., and Yahav, E. 2019. code2vec: Learning distributed representations of code. In Proceedings of the ACM on Programming Languages, S. Weirich, Ed. Association for Computing Machinery, 40–69.
- Anderson, J. R. and Reiser, B. J. 1985. The lisp tutor: it approaches the effectiveness of a human tutor. BYTE 10, 4, 159–175.
- Barnes, T. 2005. The q-matrix method: Mining student response data for knowledge. In AAAI 2005 Educational Data Mining Workshop, J. Beck, Ed. Association for the Advancement of Artificial Intelligence (AAAI), 39–46.
- Barria-Pineda, J., Guerra-Hollstein, J., and Brusilovsky, P. 2018. A fine-grained open learner model for an introductory programming course. In Proceedings of the 26th Conference on User Modeling, Adaptation and Personalization, D. Chin and L. Chen, Eds. Association for Computing Machinery, 53–61.
- Blikstein, P. 2011. Using learning analytics to assess students’ behavior in open-ended programming tasks. In Proceedings of the 1st International Conference on Learning Analytics and Knowledge, G. Conole and D. Gašević, Eds. Association for Computing Machinery, 110–116.
- Caruana, R. 1997. Multitask learning. Machine learning 28, 41–75.
- Cen, H., Koedinger, K., and Junker, B. 2006. Learning factors analysis – a general method for cognitive model evaluation and improvement. In Intelligent Tutoring Systems, M. Ikeda, K. D. Ashley, and T.-W. Chan, Eds. Springer, 164–175.
- Chi, M., Koedinger, K., Gordon, G., and Jordan, P. 2011. Instructional factors analysis: A cognitive model for multiple instructional interventions. In EDM 2011 4th International Conference on Educational Data Mining, M. Pechenizkiy, T. Calders, C. Conati, S. Ventura, C. Romero, and J. Stamper, Eds. International Educational Data Mining Society, 61–70.
- Clark, R. E., Feldon, D. F., van Merriënboer, J. J., Yates, K. A., and Early, S. 2008. Cognitive task analysis. In Handbook of research on educational communications and technology, D. Jonassen, M. J. Spector, M. Driscoll, M. D. Merrill, J. van Merrienboer, and M. P. Driscoll, Eds. Routledge, New York, NY, 577–593.
- Cleuziou, G. and Flouvat, F. 2021. Learning student program embeddings using abstract execution traces. In 14th International Conference on Educational Data Mining, S. Hsiao and S. Sahebi, Eds. International Educational Data Mining Society, 252–262.
- Cooke, N. J. 1994. Varieties of knowledge elicitation techniques. International journal of human-computer studies 41, 6, 801–849.
- Corbett, A. T. and Anderson, J. R. 1994. Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction 4, 253–278.
- De Boer, P.-T., Kroese, D. P., Mannor, S., and Rubinstein, R. Y. 2005. A tutorial on the cross-entropy method. Annals of operations research 134, 19–67.
- Edwards, S. H. and Murali, K. P. 2017. Codeworkout: short programming exercises with built-in data collection. In Proceedings of the 2017 ACM conference on innovation and technology in computer science education, G. Rößling and I. Polycarpou, Eds. Association for Computing Machinery, 188–193.
- Emerson, A., Smith, A., Rodriguez, F. J., Wiebe, E. N., Mott, B. W., Boyer, K. E., and Lester, J. C. 2020. Cluster-based analysis of novice coding misconceptions in block-based programming. In Proceedings of the 51st ACM Technical Symposium on Computer Science Education, S. Heckman, P. Cutter, and A. Monge, Eds. Association for Computing Machinery, 825–831.
- Fein, B., Grassl, I., Beck, F., and Fraser, G. 2022. An evaluation of code2vec embeddings for scratch. In Proceedings of the 15th International Conference on Educational Data Mining (EDM) 2022, T. Mitrovic and N. Bosch, Eds. International Educational Data Mining Society, 368–375.
- Fein, B., Obermüller, F., and Fraser, G. 2022. Catnip: An automated hint generation tool for scratch. In Proceedings of the 27th ACM Conference on on Innovation and Technology in Computer Science Education, E. Barendsen and Simon, Eds. Association for Computing Machinery, 124–130.
- Feng, Z., Guo, D., Tang, D., Duan, N., Feng, X., Gong, M., Shou, L., Qin, B., Liu, T., Jiang, D., and Zhou, M. 2020. CodeBERT: A pre-trained model for programming and natural languages. In The 2020 Conference on Empirical Methods in Natural Language Processing, T. Cohn, Y. He, and Y. Liu, Eds. Association for Computational Linguistics, 1536–1547.
- Fleiss, J. L., Levin, B., and Paik, M. C. 2013. Statistical methods for rates and proportions. john wiley & sons.
- Gervet, T., Koedinger, K., Schneider, J., Mitchell, T., et al. 2020. When is deep learning the best approach to knowledge tracing? Journal of Educational Data Mining 12, 3, 31–54.
- Gonçalves, J. A. and Santos, A. L. 2023. Jinter: A hint generation system for java exercises. In Proceedings of the 2023 Conference on Innovation and Technology in Computer Science Education, Simon and J. Sheard, Eds. Association for Computing Machinery, 375–381.
- Graesser, A. C., Hu, X., and Sottilare, R. 2018. Intelligent tutoring systems. In International handbook of the learning sciences, F. Fischer, C. E. Hmelo-Silver, S. R. Goldman, and P. Reimann, Eds. Routledge, England, UK, 246–255.
- Hellas, A., Ihantola, P., Petersen, A., Ajanovski, V. V., Gutica, M., Hynninen, T., Knutas, A., Leinonen, J., Messom, C., and Liao, S. N. 2018. Predicting academic performance: A systematic literature review. In Proceedings Companion of the 23rd Annual ACM Conference on Innovation and Technology in Computer Science Education. Association for Computing Machinery, 175–199.
- Hoq, M., Brusilovsky, P., and Akram, B. 2023. Analysis of an explainable student performance prediction model in an introductory programming course. In Proceedings of the 16th International Conference on Educational Data Mining (EDM) 2023, M. Feng, T. Käser, and P. Talukdar, Eds. International Educational Data Mining Society, 79–90.
- Hosseini, R. and Brusilovsky, P. 2013. Javaparser: A fine-grain concept indexing tool for java problems. In The First Workshop on AI-supported Education for Computer Science. CEUR Workshops, 60–63.
- Huang, S., Liu, Z., Zhao, X., Luo, W., and Weng, J. 2023. Towards robust knowledge tracing models via k-sparse attention. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval, M. P. Kato, J. Mothe, and B. Poblete, Eds. Association for Computing Machinery, 2441–2445.
- Jiang, B., Zhao, W., Zhang, N., and Qiu, F. 2022. Programming trajectories analytics in block-based programming language learning. Interactive Learning Environments 30, 1, 113–126.
- Jin, W., Barnes, T., Stamper, J., Eagle, M. J., Johnson, M. W., and Lehmann, L. 2012. Program representation for automatic hint generation for a data-driven novice programming tutor. In Proceedings of the 11th International Conference on Intelligent Tutoring Systems, S. A. Cerri, W. J. Clancey, G. Papadourakis, and K. Panourgia, Eds. Springer, 304–309.
- Kamberovic, M., Krivic, S., Delic, A., Szedmak, S., and Ljubovic, V. 2023. Personalized learning systems for computer science students: Analyzing and predicting learning behaviors using programming error data. In Adjunct Proceedings of the 31st ACM Conference on User Modeling, Adaptation and Personalization, S. Pera and J. Neidhardt, Eds. Association for Computing Machinery, 86–91.
- Kinnebrew, J. S., Segedy, J. R., and Biswas, G. 2014. Analyzing the temporal evolution of students’ behaviors in open-ended learning environments. Metacognition and learning 9, 187–215.
- Koedinger, K. R., Corbett, A. T., and Perfetti, C. 2012. The knowledge-learning-instruction framework: Bridging the science-practice chasm to enhance robust student learning. Cognitive science 36, 5, 757–798.
- Labra, C. and Santos, O. C. 2023. Exploring cognitive models to augment explainability in deep knowledge tracing. In Adjunct Proceedings of the 31st ACM Conference on User Modeling, Adaptation and Personalization. Association for Computing Machinery, 220–223.
- MacLellan, C. J., Harpstead, E., Aleven, V., and Koedinger, K. R. 2015. Trestle: Incremental learning in structured domains using partial matching and categorization. In Proceedings of the 3rd Annual Conference on Advances in Cognitive Systems, A. Goel and M. Riedl, Eds. Cognitive Systems Foundation, 192–210.
- Maniktala, M., Cody, C., Isvik, A., Lytle, N., Chi, M., and Barnes, T. 2020. Extending the hint factory for the assistance dilemma: A novel, data-driven helpneed predictor for proactive problem-solving help. Journal of Educational Data Mining 12, 4 (Dec), 24–65.
- Mao, Y., Shi, Y., Marwan, S., Price, T. W., Barnes, T., and Chi, M. 2021. Knowing “when” and “where”: Temporal-astnn for student learning progression in novice programming tasks. In Proceedings of the 14th International Conference on Educational Data Mining (EDM 2021), S. Hsiao and S. Sahebi, Eds. International Educational Data Mining Society, 172–182.
- Marwan, S., Shi, Y., Menezes, I., Chi, M., Barnes, T., and Price, T. W. 2021. Just a few expert constraints can help: Humanizing data-driven subgoal detection for novice programming. In Proceedings of the 14th International Conference on Educational Data Mining (EDM 2021), S. Hsiao and S. Sahebi, Eds. International Educational Data Mining Society, 68–80.
- McNamara, D. S., Crossley, S. A., and Roscoe, R. 2013. Natural language processing in an intelligent writing strategy tutoring system. Behavior research methods 45, 499–515.
- Moré, J. J., Garbow, B. S., and Hillstrom, K. E. 1980. User guide for minpack-1. Tech. rep.
- Morshed Fahid, F., Tian, X., Emerson, A., B. Wiggins, J., Bounajim, D., Smith, A., Wiebe, E., Mott, B., Elizabeth Boyer, K., and Lester, J. 2021. Progression trajectory-based student modeling for novice block-based programming. In Proceedings of the 29th ACM Conference on User Modeling, Adaptation and Personalization, N. Tintarev and M. Tkalcic, Eds. Association for Computing Machinery, 189–200.
- Muldner, K., Wixon, M., Rai, D., Burleson, W., Woolf, B., and Arroyo, I. 2015. Exploring the impact of a learning dashboard on student affect. In Artificial Intelligence in Education: 17th International Conference, C. Conati, N. Heffernan, A. Mitrovic, and M. F. Verdejo, Eds. Springer, 307–317.
- Newell, A. and Rosenbloom, P. S. 2013. Mechanisms of skill acquisition and the law of practice. In Cognitive skills and their acquisition, J. R. Anderson, Ed. Psychology Press, 1–55.
- Nguyen, H., Wang, Y., Stamper, J., and McLaren, B. M. 2019. Using knowledge component modeling to increase domain understanding in a digital learning game. In Proceedings of The 12th International Conference on Educational Data Mining (EDM 2019), C. Lynch and A. Merceron, Eds. International Educational Data Mining Society, 139–148.
- Paassen, B., Hammer, B., Price, T. W., Barnes, T., Gross, S., Pinkwart, N., et al. 2018. The continuous hint factory-providing hints in vast and sparsely populated edit distance spaces. Journal of Educational Data Mining 10, 1, 1–35.
- Pandey, S. and Srivastava, J. 2020. Rkt: relation-aware self-attention for knowledge tracing. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, P. Cui, E. Rundensteiner, D. Carmel, Q. He, and J. X. Yu, Eds. Association for Computing Machinery, 1205–1214.
- Pavlik, P. I., Cen, H., and Koedinger, K. R. 2009. Performance factors analysis –a new alternative to knowledge tracing. In Proceedings of the 2009 Conference on Artificial Intelligence in Education, V. Dimitrova, R. Mizoguchi, B. du Boulay, and A. C. Graesser, Eds. IOS Press, 531–538.
- Perkins, D. N. and Martin, F. 1986. Fragile knowledge and neglected strategies in novice programmers. In The First Workshop on Empirical Studies of Programmers on Empirical Studies of Programmers, E. Soloway, Ed. Association for Computing Machinery, 213–229.
- Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L. J., and Sohl-Dickstein, J. 2015. Deep knowledge tracing. In Advances in Neural Information Processing Systems, C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett, Eds. Neural Information Processing Systems Foundation, 505–513.
- Price, T. W., Hovemeyer, D., Rivers, K., Gao, G., Bart, A. C., Kazerouni, A. M., Becker, B. A., Petersen, A., Gusukuma, L., Edwards, S. H., and Babcock, D. 2020. Progsnap2: A flexible format for programming process data. In Proceedings of the 2020 ACM Conference on Innovation and Technology in Computer Science Education, A. Luxton-Reilly and M. Divitini, Eds. Association for Computing Machinery, 356–362.
- Price, T. W., Zhi, R., and Barnes, T. 2017. Hint generation under uncertainty: The effect of hint quality on help-seeking behavior. In International Conference on Artificial Intelligence in Education, E. André, R. Baker, X. Hu, M. M. T. Rodrigo, and B. du Boulay, Eds. Springer, 311–322.
- Rivers, K., Harpstead, E., and Koedinger, K. 2016. Learning curve analysis for programming: Which concepts do students struggle with? In Proceedings of the 2016 ACM Conference on International Computing Education Research, B. Dorn, J. Sheard, J. Tenenberg, and D. Chinn, Eds. Association for Computing Machinery, 143–151.
- Rivers, K. and Koedinger, K. R. 2017. Data-driven hint generation in vast solution spaces: a self-improving python programming tutor. International Journal of Artificial Intelligence in Education 27, 37–64.
- Salden, R. J., Aleven, V. A., Renkl, A., and Schwonke, R. 2009. Worked examples and tutored problem solving: redundant or synergistic forms of support? Topics in Cognitive Science 1, 1, 203–213.
- Schmucker, R., Wang, J., Hu, S., and Mitchell, T. 2022. Assessing the knowledge state of online students-new data, new approaches, improved accuracy. Journal of Educational Data Mining 14, 1, 1–45.
- Selent, D., Patikorn, T., and Heffernan, N. 2016. Assistments dataset from multiple randomized controlled experiments. In Proceedings of the Third (2016) ACM Conference on Learning @ Scale, V. Aleven, J. Kay, and I. Roll, Eds. Association for Computing Machinery, 181–184.
- Shen, S., Liu, Q., Chen, E., Huang, Z., Huang, W., Yin, Y., Su, Y., and Wang, S. 2021. Learning process-consistent knowledge tracing. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, H. Wang, I. Skrypnyk, W. Hsu, and S. Chawla, Eds. Association for Computing Machinery, 1452–1460.
- Shi, Y. 2023. Interpretable code-informed learning analytics for cs education. In Companion Proceedings of the 13th International Learning Analytics and Knowledge Conference. Society for Learning Analytics Research, 180–187.
- Shi, Y., Chi, M., Barnes, T., and Price, T. 2022. Code-dkt: A code-based knowledge tracing model for programming tasks. In In Proceedings of the 15th International Conference on Educational Data Mining (EDM) 2022, T. Mitrovic and N. Bosch, Eds. International Educational Data Mining Society, 50–61.
- Shi, Y., Mao, Y., Barnes, T., Chi, M., and Price, T. W. 2021. More with less: Exploring how to use deep learning effectively through semi-supervised learning for automatic bug detection in student code. In International Conference on Educational Data Mining, S. Hsiao and S. Sahebi, Eds. International Educational Data Mining Society, 446–453.
- Shi, Y. and Price, T. 2022. An overview of code2vec in student modeling for programming education. MMTC Communications-Frontiers 17, 3, 17–24.
- Shi, Y., Schmucker, R., Chi, M., Barnes, T., and Price, T. 2023. Kc-finder: Automated knowledge component discovery for programming problems. In Proceedings of the 16th International Conference on Educational Data Mining (EDM) 2023, M. Feng, T. Käser, and P. Talukdar, Eds. International Educational Data Mining Society, 28–39.
- Shi, Y., Shah, K., Wang, W., Marwan, S., Penmetsa, P., and Price, T. 2021. Toward semi-automatic misconception discovery using code embeddings. In LAK21: 11th International Learning Analytics and Knowledge Conference, N. Dowell, S. Joksimovic, M. Scheffel, and G. Siemens, Eds. Association for Computing Machinery, 606–612.
- Shute, V. J. 2008. Focus on formative feedback. Review of educational research 78, 1, 153–189.
- Snoddy, G. S. 1926. Learning and stability: a psychophysiological analysis of a case of motor learning with clinical applications. Journal of Applied Psychology 10, 1, 1.
- Tobias, S., Fletcher, J. D., and Wind, A. P. 2014. Game-based learning. Handbook of research on educational communications and technology 1, 485–503.
- Torrey, L. and Shavlik, J. 2010. Transfer learning. In Handbook of research on machine learning applications and trends: algorithms, methods, and techniques, E. S. Olivas, J. D. M. Guerrero, M. M. Sober, J. R. M. Benedito, and A. J. S. Lopez, Eds. IGI global, 242–264.
- Wang, L., Sy, A., Liu, L., and Piech, C. 2017. Learning to represent student knowledge on programming exercises using deep learning. In Proceedings of the 10th International Conference on Educational Data Mining (EDM 2017), A. Hershkovitz and L. Paquette, Eds. International Educational Data Mining Society, 324–329.
- Wick, M., Stevenson, D., and Wagner, P. 2005. Using testing and junit across the curriculum. ACM SIGCSE Bulletin 37, 1, 236–240.
- Wiggins, J. B., Fahid, F. M., Emerson, A., Hinckle, M., Smith, A., Boyer, K. E., Mott, B., Wiebe, E., and Lester, J. 2021. Exploring novice programmers’ hint requests in an intelligent block-based coding environment. In Proceedings of the 52nd ACM Technical Symposium on Computer Science Education, P. Cutter, A. Monge, and J. Sheard, Eds. Association for Computing Machinery, 52–58.
- Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A., Salakhudinov, R., Zemel, R., and Bengio, Y. 2015. Show, attend and tell: Neural image caption generation with visual attention. In International Conference on Machine Learning, F. Bach and D. Blei, Eds. PMLR, 2048–2057.
- Yang, S., Zhu, M., Hou, J., and Lu, X. 2020. Deep knowledge tracing with convolutions.
- Yudelson, M., Hosseini, R., Vihavainen, A., and Brusilovsky, P. 2014. Investigating automated student modeling in a java mooc. In In Proceedings of the 7th International Conference on Educational Data Mining (EDM) 2014, J. Stamper, Z. Pardos, M. Mavrikis, and B. M. McLaren, Eds. International Educational Data Mining Society, 261–264.
- Zhang, J., Shi, X., King, I., and Yeung, D.-Y. 2017. Dynamic key-value memory networks for knowledge tracing. In Proceedings of the 26th International Conference on World Wide Web, E. Agichtein and E. Gabrilovich, Eds. Association for Computing Machinery, 765–774.