Abstract
Knowledge graphs are effective tools for organizing information. In this work, we focus on a specialized type of Knowledge Graph called an Educational Knowledge Graph (\(EKG\)), with prerequisite relations forming paths that students can follow in their learning process. An \(EKG\) provides several features, including a comprehensive visual representation of the learning domain, and offers students alternative learning paths. The manual construction of \(EKG\)s is a time-consuming and labor-intensive task, requiring domain experts to evaluate each concept pair to identify prerequisite relations. To address this challenge, we propose a methodology that combines machine learning techniques and expert knowledge. We first introduce a prerequisite scoring mechanism for concept pairs based on semantic references captured through word embeddings. Concept pairs are then ranked with respect to their scores, and pairs with high scores are selected for expert evaluation, reducing the total number of pairs to be evaluated. The expert is iteratively presented with a concept pair, and an \(EKG\) is dynamically constructed in the background based on the expert’s label. As the graph evolves, some prerequisites can be inferred based on the existing ones, further reducing the expert’s task. We implemented our methodology in a web application, allowing experts to interact with the system and create their own graphs. Evaluations on real-life benchmark datasets show that our AI-assisted graph construction methodology forms accurate graphs and significantly reduces expert effort during the process. Further experiments conducted on a dataset from an educational platform demonstrate that students who study concept pairs in a prerequisite order determined by our methodology have a better overall success rate indicating that \(EKG\)s can improve learning outcomes in education. Interested readers can access additional material and the dataset at our Github repository1.Keywords
1. Introduction
Knowledge graphs (\(KG\)s) are developed to organize data sources and enable reasoning based on the integrated data. In simple terms, a \(KG\) is a data structure that stores information about entities such as people, places, things, concepts, etc., and their relations. In this paper, our main focus is a distinct type of \(KG\), termed an Educational Knowledge Graph (\(EKG\)), which is designed to show the relations among concepts within an education domain. Among the possible relations connecting different concepts, we chose the prerequisite relation. Although it’s challenging to extract, it helps students make more informed choices about their learning paths. With \(EKG\)s, students are offered a visual representation of a domain in education as well as different learning paths through prerequisite relations. Instructors can also build and maintain their curriculum as an \(EKG\), together with teaching materials and learning objectives. Although we only consider the prerequisite relation, other relations such as more/less difficult can also be included in an \(EKG\). In this work, we first establish a formalism for expressing \(EKG\)s based on prerequisites and propose a methodology that we call \(ACE\) for the AI-assisted Construction of Educational KGs. In fact, the manual construction of an \(EKG\) places a substantial burden on experts, as they must carefully evaluate each concept pair to determine possible prerequisite relations. It is also challenging for the expert to identify all the indirect prerequisite relations among concepts that arise due to the transitivity property of the prerequisite relation (i.e. if \(A\) is a prerequisite of \(B\) and \(B\) is a prerequisite of \(C\), then \(A\) is a prerequisite of \(C\)). To address these challenges, ACE combines machine learning techniques with expert knowledge and enables accurate construction of \(EKG\)s containing numerous concepts without requiring experts to assess all combinations of concept pairs individually. Our first contribution is a Prerequisite Rank Scoring (\(PRS\)) mechanism which ranks all the concept pairs within a concept set according to their likelihood of forming a prerequisite relation for expert evaluation. Our second contribution is an iterative strategy that consults the expert for high-ranked concept pairs and dynamically updates the \(EKG\) based on the expert’s answers. Prerequisite pairs that can be inferred from the current \(EKG\) are eliminated from the list to further reduce the expert effort.
The main research challenge for constructing an \(EKG\) is building a model to assign prerequisite scores to concept pairs in a given domain. The existing methods in the literature treat prerequisite detection as a binary decision problem and do not provide a ranking mechanism among the prerequisite candidates. Furthermore, they rely on external features such as the Wikipedia page information of the concepts (Miaschi et al., 2019), the student exam results (Chen et al., 2018), or a specific book (Adorni et al., 2019) to determine the prerequisites. ACE methodology has two advantages over the state-of-the-art: (1) It only uses the plain text descriptions of the concepts to infer prerequisite relations without requiring external resources, and (2) it is able to produce a prerequisite score for any given concept pair.
We implemented the ACE methodology as a web application2. Experts can interact with the system to form their \(EKG\)s for a desired domain. Students can also use the implemented system to see the \(EKG\)s of the domain that they are interested in. The ACE system can further generate larger labeled data sets for training supervised models for prerequisite identification. We evaluate the ACE methodology using benchmark datasets and \(EKG\)s that we obtained from an e-learning site specialized in machine learning topics. Experimental results demonstrate that our methodology enables experts to construct accurate \(EKG\)s with many concepts in a relatively short time. Further evaluation results on real-life datasets also show that students learning the concepts based on the prerequisite scores of our algorithm perform better than students who do not.
Our main contributions can be summarized as follows:
- We introduce a formalism for expressing \(EKG\)s and provide a comprehensive methodology for their construction.
- We present a novel unsupervised scoring method that can identify and rank potential prerequisite pairs in a given concept set without requiring any initial training data.
- We offer the ACE web application that can be used by both experts and students. Experts can create their own \(EKG\)s, while students can observe the paths in the constructed \(EKG\)s to understand the prerequisite relations between different concepts within a particular domain.
- We test our prerequisite ranking methodology on the real-world student exam data and show that students knowing the higher ranked prerequisites by our methodology perform better than students knowing the lower ranked prerequisites.
The rest of the paper is organized as follows: Section 2 discusses related work. In Section 3, we define the problem and terminology. Section 4 introduces our methodology to construct an \(EKG\) from a given set of concepts and their textual descriptions. In Section 5, implementation details of the ACE methodology are given. Section 6 provides the experimental evaluation, and finally, Section 7 concludes our work with an outlook on future avenues.
2. Background and Related Work
In this section, we provide background information on \(KG\)s and examples of their real-life use cases. We then introduce \(EKG\)s. Finally, we present a literature survey on prerequisite detection, one of the main relations forming \(EKG\)s.
2.1. Knowledge Graphs
\(KG\)s are composed of a network of nodes and edges, where nodes represent the entities and edges represent their relations. The most generic example is Google’s \(KG\)3, which is designed to show relations among different pieces of information so that it can provide a better understanding of what a user is searching for. \(KG\)s offer several advantages compared to other data representation models, such as the relational model and NoSQL, mainly in terms of flexibility and scalability (Hogan et al., 2021), and their use has been extended to various domains; for example, they have been applied in the tourism sector to organize festivals in Chile. The graph includes entities such as cities, events, and dates, represented by nodes, and relations between these entities, represented by directed edges with different labels. \(KG\)s also enable the deduction of new knowledge that is not explicitly stored in the graph through reasoning and inference. This involves using logical rules and algorithms to derive new facts based on existing information in the graph. For instance, in the field of recommendation systems, \(KG\)s can capture the relations between users, items, and their attributes. By reasoning over this graph, new recommendations can be generated based on the preferences and behaviors of similar users or the characteristics of similar items (Shokrzadeh et al., 2024). Another example is in the domain of healthcare, where the \(KG\)s have nodes representing a patient, a disease they are diagnosed with, and the symptoms they are experiencing. By applying reasoning techniques, the graph can deduce additional information, such as potential treatments for the disease based on known effective treatments for similar cases (Yang et al., 2024). In our work, we use the transitivity property of the prerequisite relation to derive new conclusions from existing information. Transitive relations are represented as paths that are greater than length one, and the number of such paths correspond to the number of captured new prerequisite information among nodes in our \(KG\)s.
\(KG\)s in educational contexts, also sometimes referred to as concept maps, usually represent abstract ideas and principles rather than concrete real-life objects. Concept maps are visualization frameworks that illustrate the relationships between various concepts within a specific educational domain (Novak and Cañas, 2006). Using this means of visualization has been shown to be beneficial for learners on multiple levels, such as improved knowledge retention, a more satisfactory learning experience, reduced cognitive load, and better learning achievements (Novak, 2010, Chiou et al., 2015, Furtado et al., 2019). The initial works on concept maps assume that domain experts manually construct them; however, later on, various attempts have been made to construct concept maps either automatically or semi-automatically. For example, Aguiar et al. (2016) construct concept maps by using natural language processing techniques (NLP) on the given text document. The resulting map has the extracted noun phrases as key concepts and verbs between them as relations. However, precision (29%) and recall (44%) scores were low when comparing the identified relations of the automatically constructed concept maps with concept maps constructed by experts. Lee et al. (2015) adopted another approach which consists of utilizing burst analysis of words to establish relations between terms. Meanwhile, Hirashima et al. (2015) propose a semi-automatic method through which instructors and students collaboratively construct concept maps where instructors provide students with the concepts and students are asked to define the possible relations.
These approaches often assume an unlimited number of possible relations among concepts, making it challenging to fully automate the construction of concept maps (Pinandito et al., 2021).
2.2. Prerequisite Relation Identification
Extraction of prerequisite relations among educational concepts from textual data is a challenging task and an active area of research. One way this has been pursued is through establishing pairwise concept prerequisite relations among Wikipedia articles, starting with the work of Talukdar and Cohen (2012). Subsequently, other methods are developed to detect prerequisite relations between Wikipedia articles, utilizing either unsupervised or supervised techniques. Most of these methods treat the titles of Wikipedia articles as concept names and the content of the articles as their textual descriptions. Wikipedia articles are connected through hyperlinks which can be used to train a supervised machine learning model as in the work of Sayyadiharikandeh et al. (2019), Liang et al. (2019) and Pan et al. (2017). In terms of unsupervised methods, the most prominent one is reference difference (RefD) (Liang et al., 2015), which makes use of the densely linked structure of Wikipedia. RefD captures prerequisite relations between pairs of concepts (\(c_i\), \(c_j\)) from their Wikipedia articles by counting how often links from \(c_i\) refer to \(c_j\) and how often links from \(c_j\) refer to \(c_i\). A prerequisite relation is established from concept \(c_j\) to \(c_i\) if the links in \(c_i\) refer to \(c_j\) more frequently than those in \(c_j\) referring to \(c_i\). Our prerequisite detection method extends the idea of RefD by applying it to unstructured text. We also extend our previous work (Aytekin et al., 2020) by incorporating the notion of semantic reference and a ranking mechanism.
Adorni et al. (2019) aim to identify prerequisite relations by exploiting temporal patterns between concepts in books. The authors combine burst analysis and the co-occurrence of concepts to identify these patterns. However, this method relies on extracting all the information from the same book to make sure that consistent temporal patterns are obtained. Molontay et al. (2020) propose a data-driven probabilistic student flow approach to characterize the prerequisite relations among university courses based on the success rates of students in those courses. Manrique et al. (2019) utilize generic knowledge graphs such as DBpedia, Wikidata, and YAGO to detect prerequisite relations. More recently, Zhang et al. (2022) introduced MHAVGAE, a multi-head attention variational graph auto-encoders model. MHAVGAE takes as input an existing knowledge graph consisting of two types of entities, concepts, and resources and estimates prerequisite relations among resources by leveraging the existing prerequisite relations. Similarly, Jia et al. (2021) discuss the automatic completion of a heterogeneous graph consisting of concepts and learning objectives.
Our methodology ACE, on the other hand, aims to construct a knowledge graph from scratch based on given concepts and their descriptions. Therefore, ACE could complement MHAVGAE by producing an initial (though incomplete) graph with some limited expert effort, which could then be fed to MHAVGAE for completion. Existing approaches described in the literature often require the inclusion of external features, such as Wikipedia page information, student course data, or known prerequisite relations, as in the case of MHAVGAE (Zhang et al., 2022), while our approach only requires the plain textual descriptions of the concepts. The complexity of certain domains can make it challenging to identify prerequisite relationships, especially when the prerequisite relation from \(A\) to \(D\) is indirect, having intermediate concepts in between, such as \(A \rightarrow B \rightarrow C \rightarrow D\). The work of Li et al. (2019) underscores the difficulty of annotation when determining prerequisite dependencies, particularly “long dependencies”. By keeping the labeled prerequisite pairs in a graph structure, we allow experts to see all of these “long dependencies” in the form of paths in the graph.
Yu et al. (2021) describes the design of one of China’s largest MOOC websites (MOOCCubeX) for adaptive learning. The website contains a repository consisting of around 4K courses, 230K videos, 358K exercises, 637K fine-grained concepts, and over 296 million raw behavioral data of more than three million students. The main research objective of MOOCCubeX is to personalize the student learning experience and recommend the best possible learning paths to students. To achieve this, both student-related and content-related data are utilized. Content-related data comprises identified concepts and pairwise prerequisite relations of those concepts. Due to the massive size of the unlabeled pairs, experts manually label a small portion of them, which is then used by a neural network as training data. The trained NN then predicts the prerequisite relations of the unlabeled pairs by assigning probability scores to each of them. The experts evaluate these probability scores, and verified pairs are included in a separate pool. Another group of experts checks whether the prerequisite pairs in this pool form cyclic relations and, if so, removes the ones that cause cycles. Although this process is similar to our general methodology, the unsupervised nature of our prerequisite scoring algorithm eliminates the need for training data. Moreover, our iterative graph-building algorithm automatically removes pairs that can cause cycles while the expert labels the pairs. Therefore, instead of first labeling all of the pairs and then checking for cycle-forming pairs, our method performs online cycle detection and removal.
3. Preliminaries and Problem Definition
In this section, we provide the essential definitions and the terminology. We start with the preliminary definitions from Graph Theory, which will lead us to the formal definition of an \(EKG\).
Definition 1 A directed graph \( G = V, E \) consists of a set of vertices (also called nodes) \( V \) and a set of edges \( E \) that are ordered pairs of distinct vertices from \( V \).
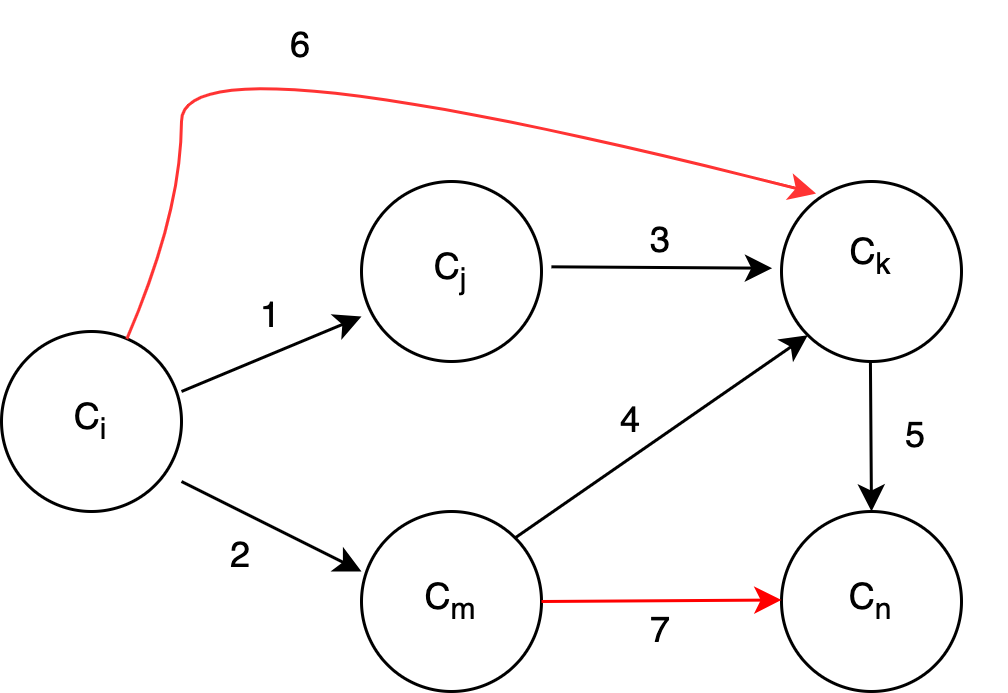
In our case, each node in a graph represents a concept; concepts are visualized as circles, while directed edges represent relations among those concepts, as shown in Figure 1a.
Definition 2 A simple directed path from node \(A\) to node \(B\) in a graph is a sequence of edges that originates at node \(A\) and terminates at node \(B\) such that we can reach \(B\) from \(A\) by following directed edges. All nodes in the path are distinct.
Definition 3 A directed edge from node \(A\) to node \(B\) is called a transitive edge if and only if there is a simple directed path from node \(A\) to node \(B\).
Figure 1a shows transitive edges in red. Transitive edges, also called redundant edges, do not provide additional connectivity information in the graph.
Definition 4 A directed acyclic graph is a directed graph with no cycles where a cycle is a sequence of edges forming a directed path starting from a node \(A\) and ending at the same node \(A\).
There may be different relations among concepts, but we concentrate on the prerequisite relation, which is fundamental for students to navigate in the graph by following different learning paths as prerequisite chains. A concept \(c_i\) is a prerequisite of another concept \(c_j\) if one must learn \(c_i\) before studying \(c_j\). The prerequisite relation has three axioms:
- Asymmetry: If concept \(c_i\) is a prerequisite of concept \(c_j\), then concept \(c_j\) cannot be a prerequisite of concept \(c_i\).
- Irreflexivity: A concept cannot be a prerequisite of itself.
- Transitivity: If concept \(c_i\) is a prerequisite of concept \(c_j\), and concept \(c_j\) is a prerequisite of concept \(c_k\), then concept \(c_i\) must also be a prerequisite of concept \(c_k\).
Definition 5 An Educational Knowledge Graph of a set of concepts \(C\), denoted by \(EKG\), is a DAG where the nodes represent the concepts, and the simple directed paths among pairs of nodes represent the prerequisite relations among the concepts.
An \(EKG\) needs to be acyclic, and the acyclicity property can be proven easily since for a cycle to appear in \(EKG\), we need to have a directed path starting from concept \(c_i\) and ending back at \(c_i\). This means that \(c_i\) is a prerequisite of \(c_i\), which violates the axiom of irreflexivity property of the prerequisite relation. A prerequisite relation could be direct or indirect, which we define based on an \(EKG\) as follows:
Definition 6 A concept \(c_i\) is an indirect prerequisite of concept \(c_j\) if and only if there is a simple path of length 2 or longer from \(c_i\) to \(c_j\) in the \(EKG\).
Definition 7 A concept \(c_i\) is a direct prerequisite of concept \(c_j\) if and only if there is a directed edge from \(c_i\) to \(c_j\) in the \(EKG\) and \(c_i\) is not an indirect prerequisite of concept \(c_j\)
Definition 8 A graph \(G_{min}\) is called a Minimal Educational Knowledge Graph of \(G\) if and only if \(G_{min}\) has the same nodes as \(G\) and \(G_{min}\) has all the edges of \(G\) except the transitive edges.
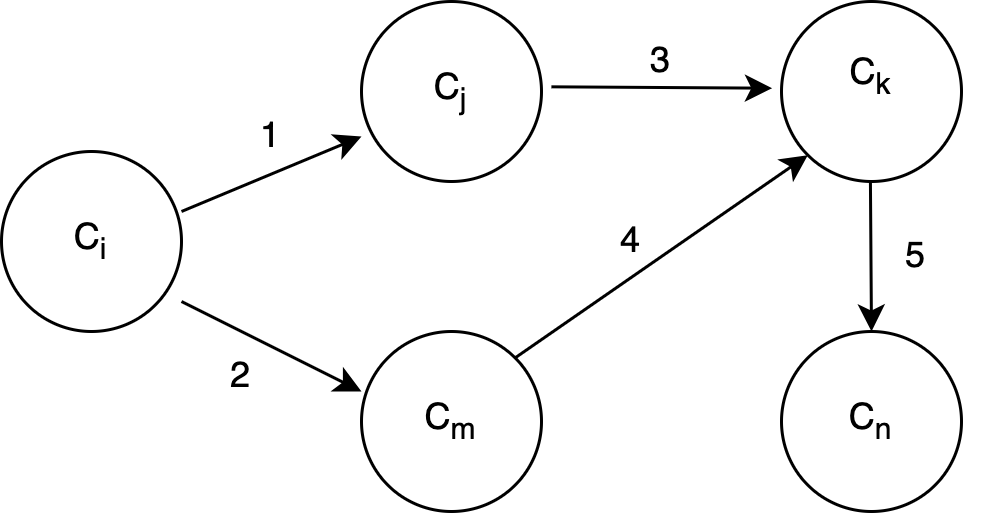
Let \(C\) be a set of concepts appearing in a domain \(D\), where each concept \(c_i \in C\) is associated with a textual description \(d_i\). Our goal is to construct an \(MEKG\), representing the concepts in \(C\) as nodes and their prerequisite relations as directed edges based on textual descriptions. In Figure 1a, we have depicted an \(EKG\) with transitive edges. We already know that concept \(c_i\) is a prerequisite of concept \(c_k\) because it is reachable from \(c_i\) (through edges 1 and 3), and concept \(c_m\) is a prerequisite of concept \(c_n\) because it is reachable from \(c_k\) (through edges 4 and 5). Because these paths already exist, edges 6 and 7 are transitive edges and should not be included in the \(MEKG\), as shown in Figure 1b.
The textual descriptions that are provided together with the concepts give us hints as to which concept is a prerequisite of another concept. We exploit those hints through deep learning models and ease the expert’s task of constructing the \(MEKG\). Details of our methodology are described in Section 4.
4. ACE Methodology for Constructing a MEKG
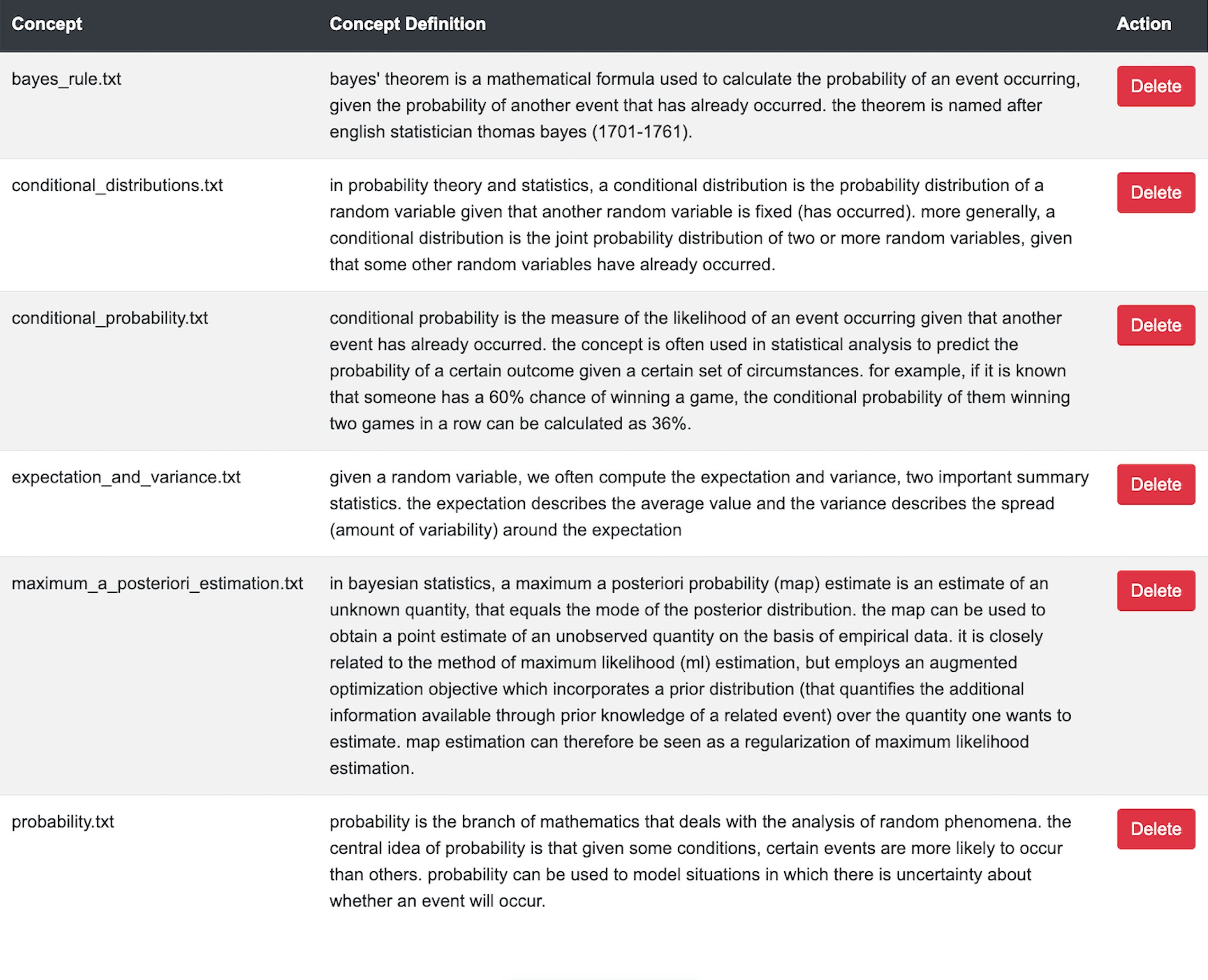
We assume that there is a domain of interest together with a set of concepts with their textual descriptions from that domain. A snapshot from our web-based application is provided as an example in Figure 2, which contains a small set of concepts with their textual descriptions. Our aim is to construct a \(MEKG\) where nodes are the concepts, and directed edges between nodes represent prerequisite relations. Our prerequisite pair-scoring mechanism for building the graph is based on the references in the textual descriptions, which could be exact references or semantic references. A concept can have different explanations, and depending on its explanation, its prerequisites can vary. Consequently, we rely on references to concept names in those explanations to identify prerequisite relationships, yet the final decision is left to the expert. The expert may determine that, although references exist, they are insufficient to establish a prerequisite relationship. Conversely, the expert might decide that a concept is a prerequisite, despite the absence of references. Therefore, by incorporating expert feedback, we improve the reliability of our \(EKG\)s in prerequisite identification. In the following subsections, we first explain the notion of semantic references as opposed to exact references. Then we describe our scoring mechanism based on semantic references.
4.1. Semantic References Versus Exact References in Prerequisite Relation Identification
If a learner frequently encounters some keywords in the textual description \(d_j\) of a concept \(c_i\) then this is an indication that one should know \(c_i\) before they may fully understand \(d_j\). Determining which keywords are related to which concept in a given textual description requires semantic analysis of the textual description. In our problem setting, we have predetermined concepts where each concept has its own textual description, and we need to check if there are references to other concepts in a given textual description. These references could be either \(exact\) or \(semantic\) references. An exact reference is identified when a concept is explicitly mentioned in the textual description, while a semantic reference is observed when keywords with a semantic connection to a concept are in the textual description. For example, let \(c_j\) be recurrent neural networks along with its description \(d_j\) and let \(c_i\) be chain rule. If we encounter specific keywords such as “derivative,” “product rule,” or “quotient rule” within the description \(d_j\), which are highly associated with the concept chain rule (\(c_i\)), we consider them as semantic references to \(c_i\) in \(d_j\). However, if we directly encounter the concept name chain rule in \(d_j\), we consider that as an exact reference to \(c_i\). Based on the frequency and prevalence of semantic and exact references to \(c_i\) in \(d_j\), we can decide if chain rule is a potential prerequisite of recurrent neural networks. The process of identifying exact references is straightforward. But, in order to capture the semantic similarity, we employ embeddings.
4.2. Embeddings for Semantic Similarity
To compute semantic similarities, each word sequence must be represented by a fixed-length vector called its embedding. Models learn embeddings through training on large amounts of textual data based on how often words appear together in the training data. By representing word sequences as fixed-length vectors, the models can compare the embeddings using metrics such as cosine similarity. Cosine similarity measures the angle between two vectors, with a smaller angle indicating a higher level of similarity. Therefore, if two word sequences have similar embeddings, their cosine similarity will be high.
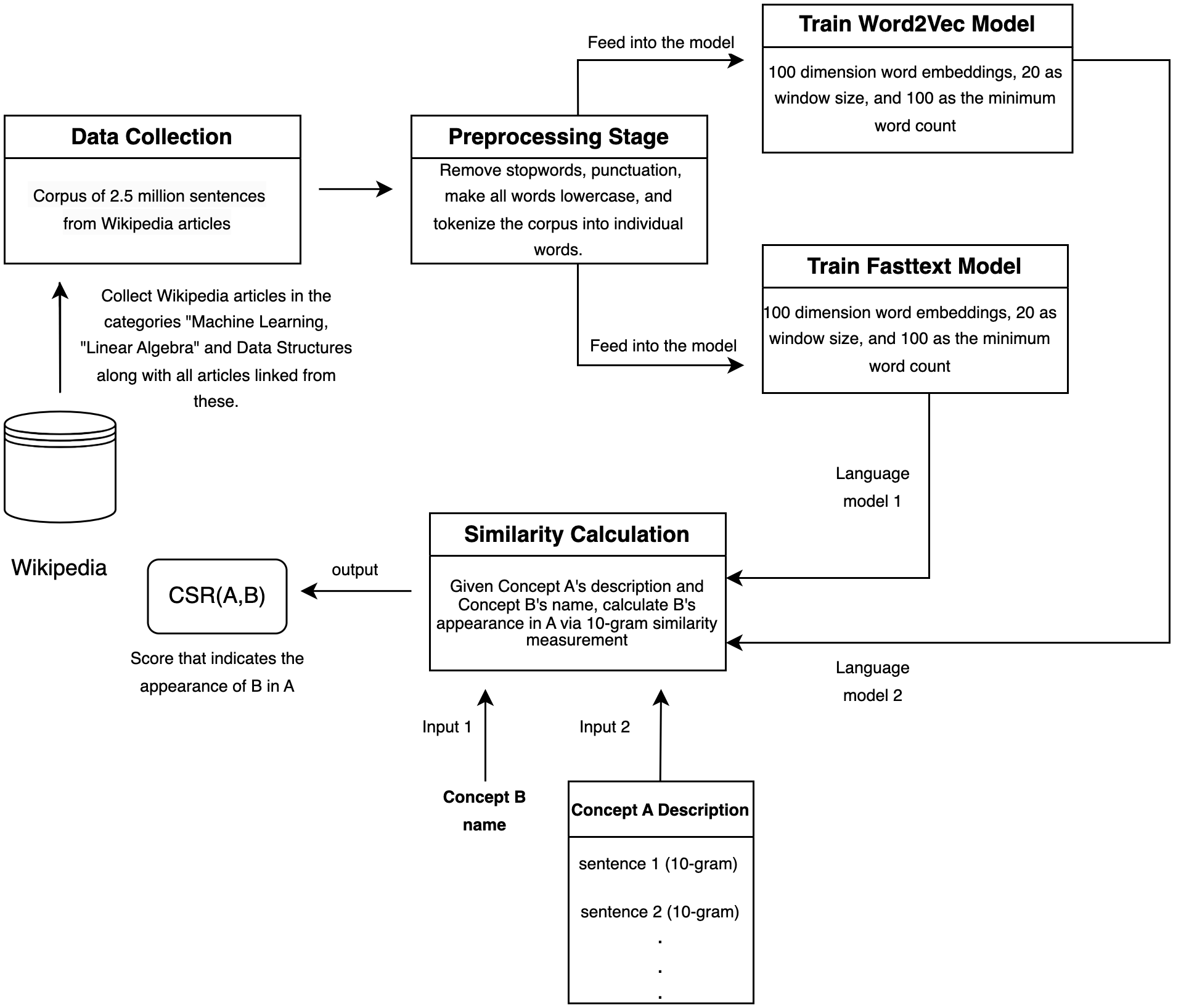
In this work, we used three models that can produce embeddings with different strategies. The first two are Word2Vec and Fasttext. These models produce fixed embeddings for the words they encounter during their training phase. We calculate the similarities between sequences of words (between a 10-gram and a concept name, which can be composed of any number of words). To be able to do this with Word2Vec and Fasttext, we represent two sequences by taking the average of the word embeddings for each individual word in the sequence. Since each embedding is a vector and vectors can have different lengths, we also make sure that the averaged vectors are unit vectors by dividing each vector by its L2 norm (Ecludian norm). Furthermore, Word2Vec cannot deal with out-of-vocabulary words (oov); therefore, if there is an oov in either of the sequences, we exclude it from the calculation. Fasttext, on the other hand, considers each word as a combination of character n-grams. It uses these n-gram representations to generate word embeddings. Therefore for the calculations with Fasttext, we don’t check for oov because Fasttext can recognize each word even if it is oov due to its character n-gram representations.
The overall methodology for obtaining the embeddings is provided in Figure 3. For training Word2Vec and Fasttext models, we first formed a corpus that consists of Wikipedia articles that are of category “Machine Learning”, “Linear Algebra” and “Algorithms and Data Structures”. We chose these domains as we used standard \(MEKG\)s for evaluation that mainly include concepts from these areas. We also included the text of all the articles that are linked from those articles, eventually reaching a corpus of 2.5 million sentences. We then preprocess our corpus by removing stopwords and punctuation marks and by converting all words to lowercase. We tokenized the sentences into individual words and trained Word2Vec and Fasttext models on the preprocessed corpus. We used the Gensim library4 in Python to train both Word2Vec and Fasttext models.
For Word2Vec, we set the dimension of the word embeddings to 100 and trained the model with the skip-gram algorithm with a window size of 20. We also set the minimum word count to 100, meaning that words occurring less than 100 times in the corpus are excluded from the vocabulary. We trained the Word2Vec model for 10 epochs. For Fasttext, we set the dimension of the word embeddings to 100, as in the case of Word2Vec, and trained a model using a skip-gram algorithm with a window size of 20. Similarly to Word2Vec, we set the minimum word count to 100. We also set the character n-gram size to range from 3 to 6, meaning that the model considers character n-grams of lengths 3, 4, 5, and 6 during training.
The third model we employ is a more sophisticated and recent model named all-MiniLM-L6-v2, which belongs to the category of sentence-transformers models. Sentence Transformers start by employing a pre-trained language model, such as Bidirectional Encoder Representations from Transformers (BERT) (Devlin et al., 2019) or Unified pre-trained Language Model (UniLM) (Dong et al., 2019) and then train with pairs of sentences that are semantically related and non-related. The training process encourages the models to generate embeddings where semantically related sentences have close vector embeddings and non-related sentences have distant vector embeddings. The all-MiniLM-L6-v2 employs Microsoft’s MiniLM pre-trained language model5 and is fine-tuned on 1B sentence pairs for the semantic similarity task. The fine-tuned model can be downloaded from Huggingface6. Given a sentence with a maximum of 128 tokens, all-MiniLM-L6-v2 produces a fixed-length sentence vector embedding of size 384. Since the model is already fine-tuned on a very large dataset for semantic similarity tasks, we directly use the model without any further fine-tuning and analyze its effect on our prerequisite detection methodology together with the two other models (Word2Vec and Fasttext).
4.3. Scoring Based on Semantic and Exact References
Given a set of concepts \(C\) and \(c_{i}\in C\) where \(d_{i}\) is the textual description of \(c_{i}\), we calculate either of the two reference scores: the Cumulative Semantic Reference score (CSR) or the Cumulative Exact Reference score (CER).
We use a sliding window strategy to split \(d_{i}\) into n-grams, with a fixed value of \(n\) set to 10 and stride parameter \(s\) (which determines the distance that the window moves at each step) also set to 10. This is done to ensure a reasonable sentence size while simultaneously optimizing the speed and performance of the algorithm’s execution.
Let \(d_{i}\) be a textual description that contains \(x\) number of 10-grams. We denote each 10-gram of \(d_{i}\) by \(s_{ij}\), where \(0 < j \leq x\). To detect semantic references, we consider the cosine similarities between the embeddings of concept names in \(C\) and the embedding of \(s_{ij}\). We would like to note that our language model returns a single embedding for \(s_{ij}\). \(CSR\) score of pair \((c_{i},{c_k})\) is calculated as shown in Equation 1.
\begin {equation} \label {eq:csr} CSR(c_{i},c_{k}) = \sum _{j} sim_{Cosine}(s_{ij},c_{k}) \end {equation}
\(CSR\)scores are not symmetric, meaning that \(CSR(c_{i},c_{k})\) may not be equal to \(CSR(c_{k},c_{i})\) since semantic references of \(c_{k}\) in \(d_i\) are different than the semantic references of \(c_{i}\) in \(d_k\).
Exact references are identified without any word or sentence embedding. Given a concept \(c_{i}\) and its description \(d_{i}\) with 10-grams \(s_{ij}\), the formula for \(CER\) is:
\begin {equation} \label {eq:esr} CER(c_{i},c_{k}) = \sum _{j} I(s_{ij},c_{k}) \end {equation}
In this context, \(I(s_{ij},c_{k})\) is an indicator function that outputs 1 if the 10-gram contains the concept name \(c_{k}\) and returns 0 otherwise.
The prerequisite Ranking Score (\(PRS\)) is based on the \(CSR\) or \(CER\) scores of the concept pairs. For two concepts \(c_{i}\) and \(c_{k}\), a high \(CSR(c_{i},c_{k})\) or \(CSR(c_{k},c_{i})\) score indicates a strong possibility that there is a direct prerequisite relation from either \(c_{i}\) to \(c_{k}\) or \(c_{k}\) to \(c_{i}\). Although the \(CSR\) score is a good indicator for prerequisite relations, it results in false positives when it is used to determine the direction (i.e. \(c_{i} \rightarrow c_{k}\) vs \(c_{k} \rightarrow c_{i}\)), especially when \(CSR(c_{i},c_{k})\) and \(CSR(c_{k},c_{i})\) are close to each other. Therefore the \(PRS\) score is based on the maximum \(CSR\) scores as shown in Equation 3.
\begin {equation} \label {eq:prs} PRS\left ( c_{i},c_{k} \right )= \max \left \{ CSR\left (c_{i},c_{k}\right ), CSR\left (c_{k},c_{i}\right ) \right \} \end {equation}
We note that \(PRS\) is symmetric thus \(PRS(c_{i}, c_{k}) = PRS(c_{k}, c_{i})\). \(PRS\) with \(CER\) is defined similarly as shown in Equation 4.
\begin {equation} \label {eq:psre} PRS\left ( c_{i},c_{k} \right )= \max \left \{ CER\left (c_{i},c_{k}\right ), CER\left (c_{k},c_{i}\right ) \right \} \end {equation}
To identify potential prerequisite pairs, we calculate the \(PRS\) scores of all unordered pairs in the concept set and sort them according to their scores. We then consider the top \(t\) percent of the sorted pairs potential direct prerequisite pairs to be evaluated by the expert.
Algorithm: ACE Main Algorithm
Input:
\(C = \{c_1, \dots , c_m\}\) \(\triangleright \) Concepts
\(d = \{d_1, \dots , d_m \mid d_i \text { describes } c_i\in C\}\) \(\triangleright \) Textual descriptions of \(C\)
Output:
MEKG for set \(C\)
- \(\text {RL} \gets \text {rank}(C,d)\) // Rank all the unordered pairs of C according to their \(PRS\) scores.
- \(EKG = (V, E)\), where \(V = C\) and \(E = \emptyset \) // Initial graph with no edges.
-
for \(k\) in range\((0, \text {len}(RL))\) do
- \((c_i, c_j) = \text {RL}[k]\) // Pair is retrieved from the ranked list.
-
if NOT (Path \(P\langle c_i, \dots , c_j \rangle \) exists or Path \(P\langle c_j, \dots , c_i \rangle \) exists in \(EKG\))
- \(\text {answer} \gets \text {expert response}\) // Expert selects an option.
-
if \(\text {answer} == 0\) then
- \(E \gets E \cup \{c_i \rightarrow c_j\}\)
- Reduce(\(EKG\)) // Remove transitive edges.
-
else if \(\text {answer} == 1\) then
- \(E \gets E \cup \{c_j \rightarrow c_i\}\)
- Reduce(\(EKG\)) // Remove transitive edges.
-
else if \(\text {answer} == 2\) then
- break // Expert decides to finish labeling.
- end for
5. ACE Main Algorithm and System Implementation
The ACE System takes a set of concepts along with their textual descriptions as input. Figure 2 shows a sample input set. Based on the provided input, ACE forms an \(MEKG\) based on expert feedback and eliminates redundant edges. It then displays the result as shown in Figure 5. The experts can prepare concept descriptions or obtain them from existing resources. The experts also have the option to modify the descriptions by removing or adding sentences as needed.
ACE algorithm has two distinct phases. In the first phase, ACE assigns scores to all unordered pairs of the concept set \(C\) based on their \(PRS\) values as described in Section 4.3. This results in a list, \(RL\), containing all concept pairs, sorted from the most likely to the least likely to form a prerequisite relation.
In the second phase, ACE initializes the \(MEKG\) as a null graph, where \(V\) corresponds to the set of concepts and \(E\) to the set of edges which is initially empty. Subsequently, the algorithm iterates over concept pairs in \(RL\). For each pair \((c_{i}, c_{j})\), the current graph is checked to see if there is an existing path from \(c_{i}\) to \(c_{j}\) or \(c_{j}\) to \(c_{i}\). If there is a path \(P<c_i,\dots c_j>\) then we can infer that \(c_{i}\) is a prerequisite of \(c_{j}\) and similarly if a path \(P<c_j,\dots c_i>\) exists then we can infer that \(c_{j}\) is a prerequisite of \(c_{i}\). If neither of the paths exists, the algorithm asks for expert feedback, presenting the pair for evaluation. The expert’s response is obtained through a graphical user interface (GUI) and stored in the variable \(answer\). Based on the expert’s response, the algorithm takes appropriate actions to update the \(MEKG\). If the expert determines that \(c_{i}\) is a direct prerequisite of \(c_{j}\), the directed edge \(\{c_i \rightarrow c_j\}\) is added to the \(MEKG\). Alternatively, if the expert identifies \(c_{j}\) as a direct prerequisite of \(c_{i}\), the directed edge \(\{c_j \rightarrow c_i\}\) is included. The graph formation process may reveal that some of the already created edges are transitive. Such a scenario is shown in Figure 4, where red nodes in the figure indicate the current concept for which direct prerequisites are labeled. Similarly, dashed red lines indicate prerequisite candidates for labeling, whereas black edges denote actual prerequisites after the transitive edge is eliminated. Such cases are checked, and newly formed transitive edges are removed by the Reduce(\(EKG\)) operation in the algorithm. If the expert’s response does not indicate a direct prerequisite relationship, no action is taken in the current \(MEKG\). The expert can also label some of the sorted pairs and retrieve the corresponding \(MEKG\) without having to complete all the pairs in \(RL\).
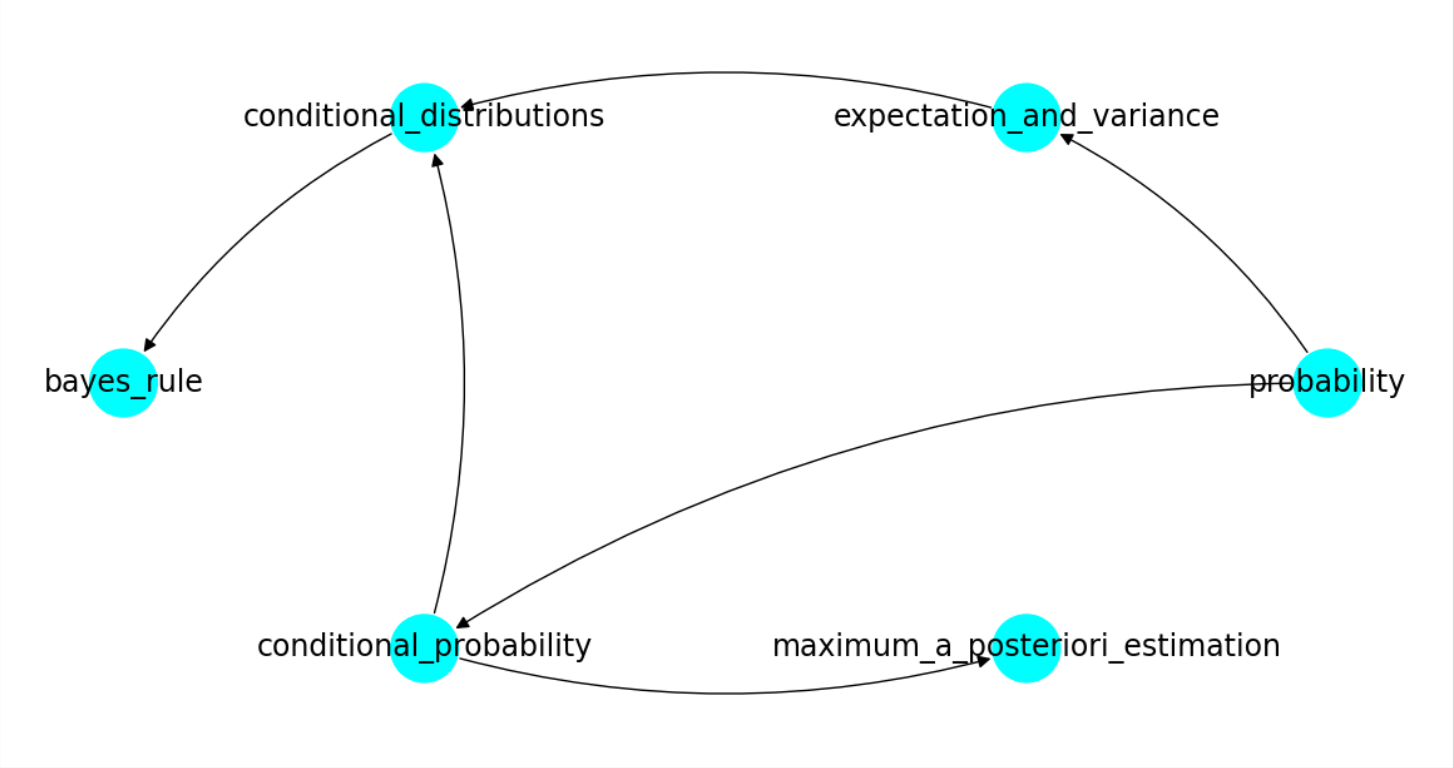
We implemented the ACE methodology in a web application. Experts can use the system to create their own \(MEKG\)s by interacting with a simple GUI. Figure 6 shows an instance where the expert decides that there is a prerequisite relation from conditional probability to bayes rule by checking the box corresponding to \(C2 \rightarrow C1\). The label \(C1\) corresponds to the name of the first concept; \(C2\) corresponds to the name of the second concept. The PRS score is also included as a reference for the expert. Each time the expert evaluates a concept pair, she can also see the resulting \(MEKG\) in the web application. Figure 5 shows an example \(MEKG\). We can see that the DAG shows the prerequisite relations among 6 concepts. Experts may also use the web application to create labeled data for training supervised algorithms on a prerequisite detection task. To do that, the ACE system has the option to convert the graph to binary labeled data in tabular form as shown in Table 1 where the presence of a simple directed path between a pair of concepts is represented by ‘1’ to indicate a prerequisite relationship from the first concept to the second concept in the pair.

| Concept 1 | Concept 2 | Label |
|---|---|---|
| C1 | C2 | 1 |
| C1 | C3 | 0 |
| C1 | C4 | 0 |
| C4 | C1 | 1 |
| C4 | C2 | 1 |
| C4 | C3 | 0 |
5.1. Role of the Expert
The involvement of an expert helps ensure the \(MEKG\) does not contain invalid edges, assuming the expert accurately assigns direct prerequisite relationships. Note that invalid edges in the graph can have a cascading effect, resulting in the formation of many invalid paths. Furthermore, references in a textual description indicate a potential prerequisite relation, but sometimes, expert assistance is needed in order to determine the direction of the relation because both descriptions can refer to each other with similar \(CSR\) scores. For example, in our evaluation study we have encountered the concept linked list whose textual description refers to concept tree as “linked list can be used to implement several other data structures such as stack and tree” and at the same time, textual description of concept tree also refers to concept linked list as “trees are implemented with linked lists” thus \(CSR(linked\; list,tree)\) and \(CSR(tree, linked\; list)\) are high and close to each other. Therefore instead of automatically assigning the prerequisite direction either from linked lists to tree or from tree to linked lists, we refer to \(PRS(linked\; list,tree)\) which is the maximum of the two \(CSR\) scores for the selected pair and ask the expert to decide.
For a concept set with \(n\) concepts, there are \(\frac {{n \cdot (n-1)}}{2}\) unordered concept pairs. For each unordered pair \(A,B\), the expert needs to evaluate whether there is a prerequisite relation from \(A\) to \(B\), from \(B\) to \(A\), or no prerequisite relation at all. If the expert evaluates approximately the top \(t\%\) of the pairs, then the expert effort is \(\left [\frac {{n \cdot (n-1)}}{2} \cdot \frac {t}{100}\right ] - d\) units, where \(d\) corresponds to the number of transitive edges that we inferred from the \(MEKG\). Since \(d\) is not a fixed value and it could be 0 in the worst case, therefore we eliminated \(d\) in theoretical calculations for simplicity. In this case the relative reduction in expert effort as: \(\frac {{n \cdot (n-1)}}{2} \cdot (1 - \frac {t}{100})\).
If \(t=100\), the expert will have considered all the concept pairs and the resulting \(MEKG\) will be identical to the gold-standard graph. However, the relative reduction will be 0. On the other hand, for \(t < 100\), the expert may miss some prerequisite pairs. According to our evaluation of real-life \(MEKG\)s constructed by the experts, as shown in Section 6, on average, between 5% - 15% of the unordered pairs have direct prerequisite relations (edges). With this in consideration, we also introduce the maximum relative reduction, which is the minimum value of \(t\) under which the expert will definitely miss some pairs that contain prerequisite relations. For example, if the standard \(MEKG\) contains 100 concepts and 495 edges, the maximum relative reduction will be equal to 90 because we have \(\frac {{100 \times 99}}{{2}} = 4950\) number of unordered pairs, and 495 of them contain a direct prerequisite relation (edges). This means that if a perfect prerequisite ranking algorithm uses \(t=10\) in this example, all 495 prerequisite pairs shown to the expert will be the true candidates, and the expert will build a standard \(MEKG\) with a maximum possible relative reduction of 90%.
6. Experimental Evaluation
In this section, we perform two experiments to test the capability of our prerequisite scoring methodology and then perform a third experiment to assess the reliability and scalability of our constructed \(MEKG\)s using the ACE algorithm.
In the first experiment, we create a supervised binary prerequisite classifier \(CSR\_bin(t)\), which turns the \(CSR\) scores of concept pairs into binary classes 0 and 1 according to a learned threshold \(t\). Class 1 is composed of pairs \((A, B)\) where there is a prerequisite relation from \(A\) to \(B\), and Class 0 is composed of pairs where there is no prerequisite relation from \(A\) to \(B\). By creating a binary supervised classifier, we can evaluate our prerequisite scoring methodology against the other well-known approaches in the literature.
We argue that concept pairs with high \(CSR\) scores have a higher number of semantic references and, therefore, are expected to have a positive correlation with student performance. In the second experiment, we assess \(CSR\) scoring methodology using a real-world student dataset (Gong et al., 2022). We claim that concept pairs \((A, B)\) having high \(CSR\) scores may indicate a prerequisite relation from \(A\) to \(B\) therefore, students knowing \(A\) should demonstrate a better performance on questions related to \(B\) than randomly selected students. To show this, we form 1000 concept pairs \((A, B)\) for which we have one control group and one treatment group. The treatment group consists of students who know the concept \(A\) and solve questions related to \(B\), and the control group consists of random students who only solve questions related to \(B\). We then show that the treatment group consistently outperforms the control group on the pairs with high \(CSR\) scores, indicating that high \(CSR\) scores and student performances are correlated.
In the third and final experiment, we evaluate the reliability of our \(MEKG\)s constructed by the ACE Algorithm. We then discuss the impact of the language model choice, the mode of the prerequisite scoring methodology (\(CSR\) or \(CER\)), and the concept set size on the runtime of our algorithm and the quality of the resulting graphs.
6.1. Prerequisite Scoring Methodology as a Supervised Binary Classifier
Prerequisite detection is treated in the literature as a binary classification problem. Given a pair \((A, B)\), the supervised models learn to predict whether a prerequisite relation exists from \(A\) to \(B\). To make a meaningful comparison with the related models in the literature, we do not use \(PRS\) with expert interaction and instead create \(CSR\_bin(t)\) which assigns \(CSR(B, A)\) scores to every pair and labels the \(t\) percent of the highest scored pairs as 1 indicating a prerequisite relation from \(A\) to \(B\), and others as 0 indicating no prerequisite relation. The parameter \(t\) is a learnable parameter, and we decide that it should be the \(t\) value that gives the highest F1 score in the training data, as both recall and precision are equally important in this task.
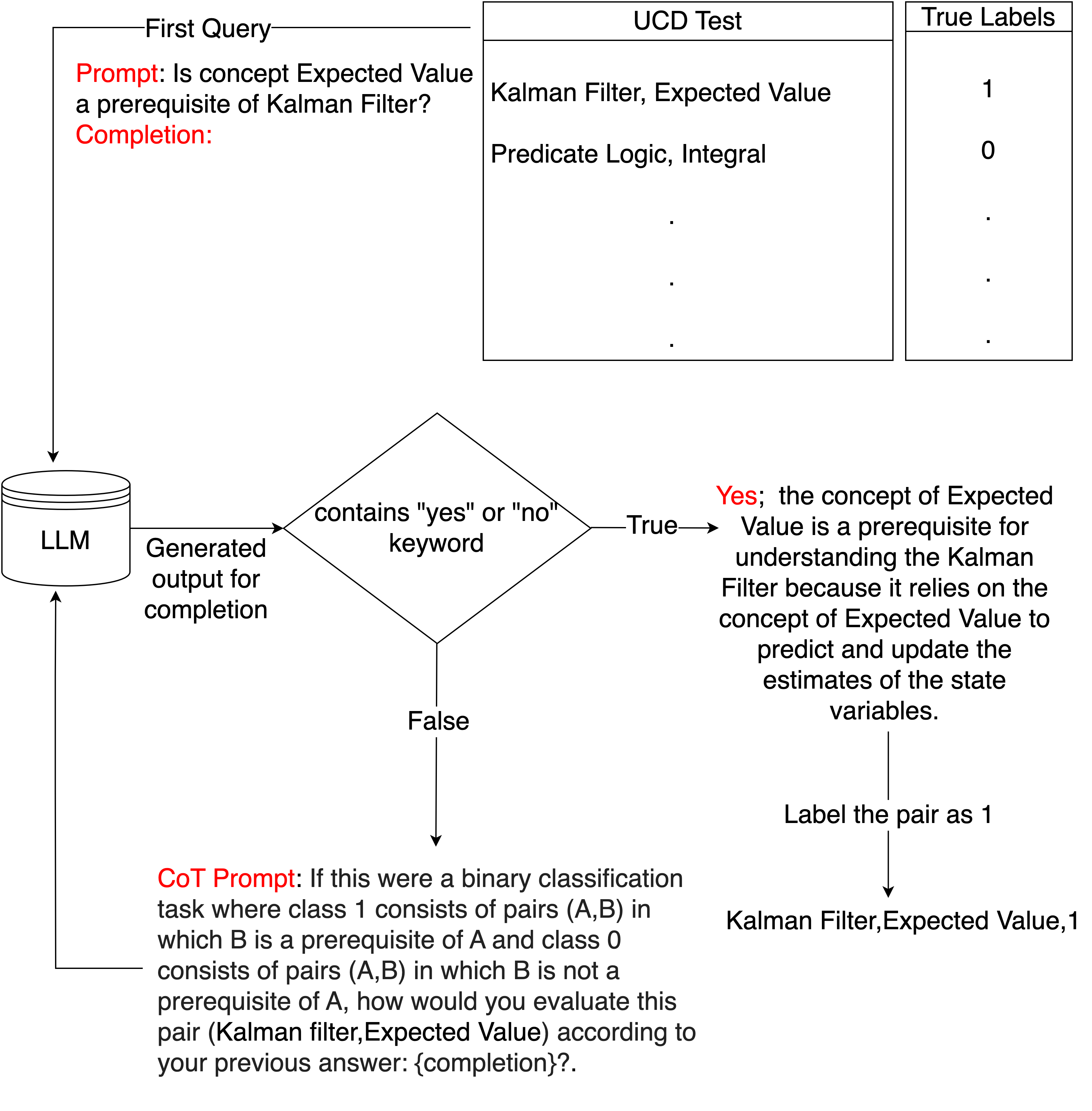
We evaluate \(CSR\_bin(t)\) on the University Course Dataset (UCD), introduced by Liang et al. (2017). UCD dataset initially contained 1008 manually annotated prerequisite concept pairs extracted from the Computer Science course syllabus of various universities in the USA. UCD was later enriched by Roy et al. (2019) by providing 1512 negative instances (i.e., non-prerequisite pairs) on top of 1008 positive pairs making it a larger and more complete dataset with 2520 pairs. The dataset can be downloaded from GitHub7. Roy et al. (2019) conducted a comparative analysis of the outcomes associated with four distinct prerequisite detection strategies applied to this dataset. Two of these strategies, developed by Pan et al. (2017) and Liang et al. (2017), are referred to as MOOC-RF and CPR-Recover and the remaining two strategies, introduced by Roy et al. (2019) are referred to as PREREQ and Pairwise LDA. Each concept pair \((A, B)\) in UCD is labeled either 0 or 1. Label 1 indicates that \(A\) is a prerequisite of \(B\), and 0 indicates that \(A\) is not a prerequisite of \(B\). Each concept in the concept pair has its corresponding Wikipedia article; therefore, the textual content in these articles is used as concept descriptions. Liang et al. (2017) report that they use 60% of UCD data as training and 40% of it as testing for all the reported models with 5-fold cross-validation. To make a fair comparison, we also use the same setup. After training, we learn the \(t\) value to be 68. In addition to the four mentioned models, we experiment with two state-of-the-art large language models and their various configurations to assess their capability to understand prerequisite relations. These models include GPT-3.5 turbo, GPT-4o-mini, GPT-4o-mini with Retrieval-Augmented Generation (RAG)8, LLAMA 3 and LLAMA 3 with RAG9. For each model, we construct the initial prompt “is concept B a prerequisite of A?” and expect the LLM to answer it with “yes” or “no” and then make an explanation. In cases where the LLMs do not give a clear response in the form of a binary decision “yes” or “no”, we use a Chain-of-Thought (CoT) prompting technique. Specifically, we give a follow-up prompt to the LLM as: “If this would be a binary classification task where class 1 consists of pairs (A, B) in which B is a prerequisite of A and class 0 consists of pairs (A, B) in which B is not a prerequisite of A, how would you evaluate this pair (A, B) according to your previous answer: + previous answer”, where the previous answer is a variable that stores the LLM’s previous output. This way, we let the LLM evaluate and make a binary decision based on its previous answer. For the experiments with GPT-3.5 turbo, LLAMA 3, and GPT-4o-mini, we send the query “is concept B a prerequisite of A?” and parse the LLM output to see if it contains a “yes” or “no” keyword. If such a keyword is not found, we use the CoT prompt to get the final output which always contains a “yes” or “no” keyword. In the case of RAG configurations, we provide two texts (textA, textB) corresponding to the Wikipedia articles of concepts A and B to the LLM. We then designed the prompt to ask whether the text of concept B is a prerequisite for understanding the text of concept A. To avoid exceeding the input size limit, we only consider the first 500 words from textA and textB. As with the other models, we use the CoT prompt if the parsed output does not contain a “yes” or “no” keyword.
| Name of the method | Precision | Recall | F1 score |
|---|---|---|---|
| PREREQ | 46.76 | 91.64 | 59.68 |
| Pairwise LDA | 98.27 | 16.42 | 28.14 |
| CPR-Recover | 16.66 | 46.51 | 24.54 |
| MOOC-RF | 43.70 | 53.43 | 50.95 |
| CSR binary classifier(t=68) | 46.13 | 1 | 66.53 |
| Zero-shot GPT-3.5 Turbo | 83.33 | 44.77 | 58.25 |
| Zero-shot GPT 4o-mini | 86.70 | 35.80 | 50.70 |
| LLAMA 3 | 72 | 62.68 | 67.02 |
| GPT 4o-mini RAG | 87.23 | 61.11 | 71.92 |
| LLAMA 3 RAG | 80.64 | 62.18 | 70.22 |
In Table 2, we compare the performance of \(CSR\_bin(t=68)\) with nine other models: PREREQ, Pairwise LDA, CPR-Recover, MOOC-RF, Zero-shot GPT-3.5 Turbo, Zero-shot GPT-4o-mini, LLAMA 3, GPT-4o-mini RAG, and LLAMA 3 RAG in terms of recall, precision, and F1 score. From the table, we can observe that \(CSR\_bin(t=68)\) outperforms traditional models such as PREREQ, Pairwise LDA, CPR-Recover, and MOOC-RF in terms of recall and overall F1 score. \(CSR\_bin(t=68)\) achieves a perfect recall score of 1, meaning all actual prerequisite pairs in the dataset were correctly identified by labeling the top 68% of the CSR-sorted pairs as prerequisites. It also achieves the highest F1 score among traditional methods, with a value of 66.53. The second-best F1 score is from PREREQ at 59.68, followed by MOOC-RF at 50.95, CPR-Recover at 24.54, and Pairwise LDA at 28.14. This indicates superior overall performance in balancing precision and recall compared to traditional methods. However, in terms of precision, \(CSR\_bin(t=68)\) has a precision of 46.13, which is lower than Pairwise LDA’s precision of 98.27 but higher than CPR-Recover’s precision of 16.66. PREREQ and MOOC-RF have precisions of 46.76 and 43.70, respectively, making \(CSR\_bin(t=68)\) comparable to PREREQ and MOOC-RF in precision but significantly lower than Pairwise LDA. When comparing \(CSR\_bin(t=68)\) with large language models (LLMs) and their various configurations, we observe that LLMs like Zero-shot GPT-4o-mini (86.70), GPT-4o-mini RAG (87.23), and LLAMA 3 RAG (80.64) exhibit significantly higher precision compared to \(CSR\_bin(t=68)\)’s 46.13. Zero-shot GPT-3.5 Turbo (83.33) and LLAMA 3 (72) also show higher precision, reflecting the advancements LLMs bring in terms of accurately identifying true positives. In terms of recall, \(CSR\_bin(t=68)\)’s recall of 1 is higher than all the tested LLM configurations, which achieve recalls ranging from 35.80 (Zero-shot GPT-4o-mini) to 62.68 (LLAMA 3). This suggests that while LLMs identify prerequisites with high accuracy (precision), their ability to capture all relevant prerequisite pairs (recall) is still below that of \(CSR\_bin(t=68)\). Among the LLMs, GPT-4o-mini RAG attains the highest F1 score of 71.92, followed by LLAMA 3 RAG at 70.22 and LLAMA 3 at 67.02. Given that our goal in ACE methodology is to capture all the prerequisite relations in the respective domain and false positives can be tolerated thanks to the presence of the expert, we conclude that \(CSR\) scores demonstrate promise, particularly in educational contexts where identifying all potential prerequisites is crucial. Moreover, we also observe that simultaneously achieving high precision and recall in the context of binary prerequisite detection tasks still remains a significant challenge whether we use traditional methods or LLMs.
6.2. Testing the Correlation Between Prerequisite Scoring Methodology and Student Performance
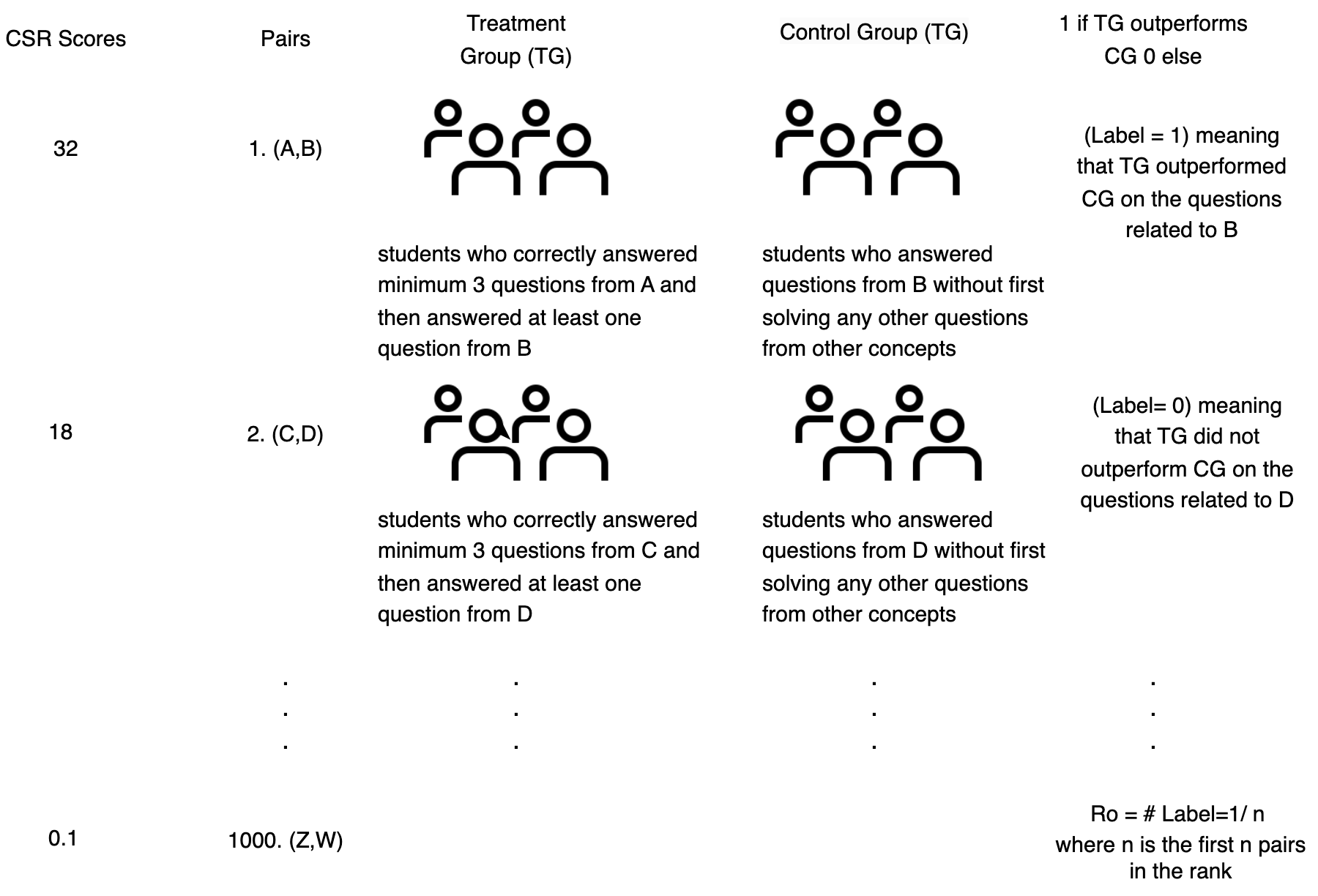
In this experiment, we test if \(CSR\) scores are correlated with student performance. Remember that \(CSR(B, A)\) is high if concept \(A\) is frequently referenced in the description of concept \(B\). In case of a high \(CSR(B, A)\) score, we expect that students who already know concept \(A\) perform better on concept \(B\) when compared to the control group. Conversely, in the case of a low \(CSR(B, A)\) score, students knowing \(A\) are not expected to have better performance on \(B\) when compared to the control group. The control group is a set of randomly selected students whose knowledge of \(A\) is not known. Figure 8 illustrates how we calculate this correlation.
To realize our experiment, we use the student logs from a dataset of a real-world educational platform (Gong et al., 2022). We partition the dataset into two tables concept_metadata.csv and student_answers.csv. The concept_metadata.csv contains 756 different secondary school mathematics concepts with columns:
- Concept IDs: A unique numerical code assigned to each concept.
- Concept Name: A descriptive title associated with each concept.
The student_answers.csv table contains 6468 unique students and their answers for questions related to these concepts with columns:
- User IDs: A unique identifier for each student.
- Concept and Question IDs: Identifiers that link each question to its corresponding concept.
- Timestamps: The exact date and time of each attempt on a question.
- IsCorrect: A binary value indicating if the student’s answer to a question is correct.
The questions are multiple-choice with four options: A, B, C, and D. We assume that a student knows a concept if she correctly answers at least three different questions related to that concept at her first attempt. Our experiment has three phases. In Phase 1, we find all possible pairs \((A, B)\) from the initial 756 unique concepts such that we can form a Treatment Group \(TG\) consisting of students who know \(A\) and solved questions related to \(B\) and a Control Group \(CG\) consisting of students who only solved questions related to \(B\). In Phase 2, we calculate the students’ average ratio of correct answers for the questions related to \(B\) for both groups to determine if \(TG\) outperforms \(CG\). In Phase 3, we sort concept pairs formed in Phase 1 based on their \(CSR\) scores to see how the average ratio of correct answers in \(TG\) and \(CG\) change for decreasing CSR scores.
In Phase 1 of our experiment, we form all ordered concept pairs \((A, B)\) from the initial 756 concepts, which corresponds to \((756 \times 755=570780)\) concept pairs. For each pair in the list, we check if both \(TG\) and \(CG\) are formed. \(TG\) is formed for pair \((A, B)\) if we can find students who correctly answered a minimum of 3 questions from \(A\) in their first attempt and answered at least one question from \(B\). \(CG\) is formed if we can find students who solve at least one question from \(B\) without first solving questions from any other concept. If both \(TG\) and \(CG\) are not formed for a pair of concepts, we discard that pair and move on to the next pair in the list. Following this methodology, we form a test set of 1000 concept pairs for which the average number of students in \(TG\) and \(CG\) are \(15.75\) and \(27.28\), respectively.
In Phase 2, for each of the 1000 concept pairs \((A, B)\), we calculate students’ average ratio of correct answers to \(B\) in \(TG\) and \(CG\). If the average ratio of \(TG\) is higher than \(CG\), we label that pair as 1, indicating that \(TG\) outperforms \(CG\), and label it as 0 if \(CG\) outperforms \(TG\). Given a sequence \(S\) of concept pairs, we count the number of concept pairs in \(S\) for which \(TG\) outperforms \(CG\) (i.e., pairs with label 1) and define the ratio of outperforming pairs over all pairs \(R_o(S)\) formally as:
\begin {equation} R_{o}(S) = \frac {1}{|S|} \sum _{i=1}^{|S|} \text {label}(S[i]) \end {equation} where label\((S[i])\) is the label of the ith concept pair in \(S\), and \(|S|\) is the number of concept pairs in \(S\).
The third and final phase of our experiment begins with the calculation of \(CSR\) scores of the 1000 concept pairs \((A, B)\) that we obtained in Phase 1. Our benchmark data set does not contain the textual descriptions of concepts, therefore in order to calculate \(CSR\) scores through semantic references, we opted to use GPT-3 to generate the textual descriptions. We then calculate \(CSR\) scores based on those descriptions and sort the concept pairs \((A, B)\) in descending order of \(CSR(B, A)\). The sorted list of 1000 concept pairs is then partitioned into 10 subsequences \(S_1, S_2,..., S_{10}\), each containing 100 concept pairs such that \(S_{1}\) has the top 100 concept pairs, \(S_{2}\) contains the next 100 concepts and so on. Finally, we calculate \(R_o(S_j)\) for each of \(S_j\) for \(1<j<10\).
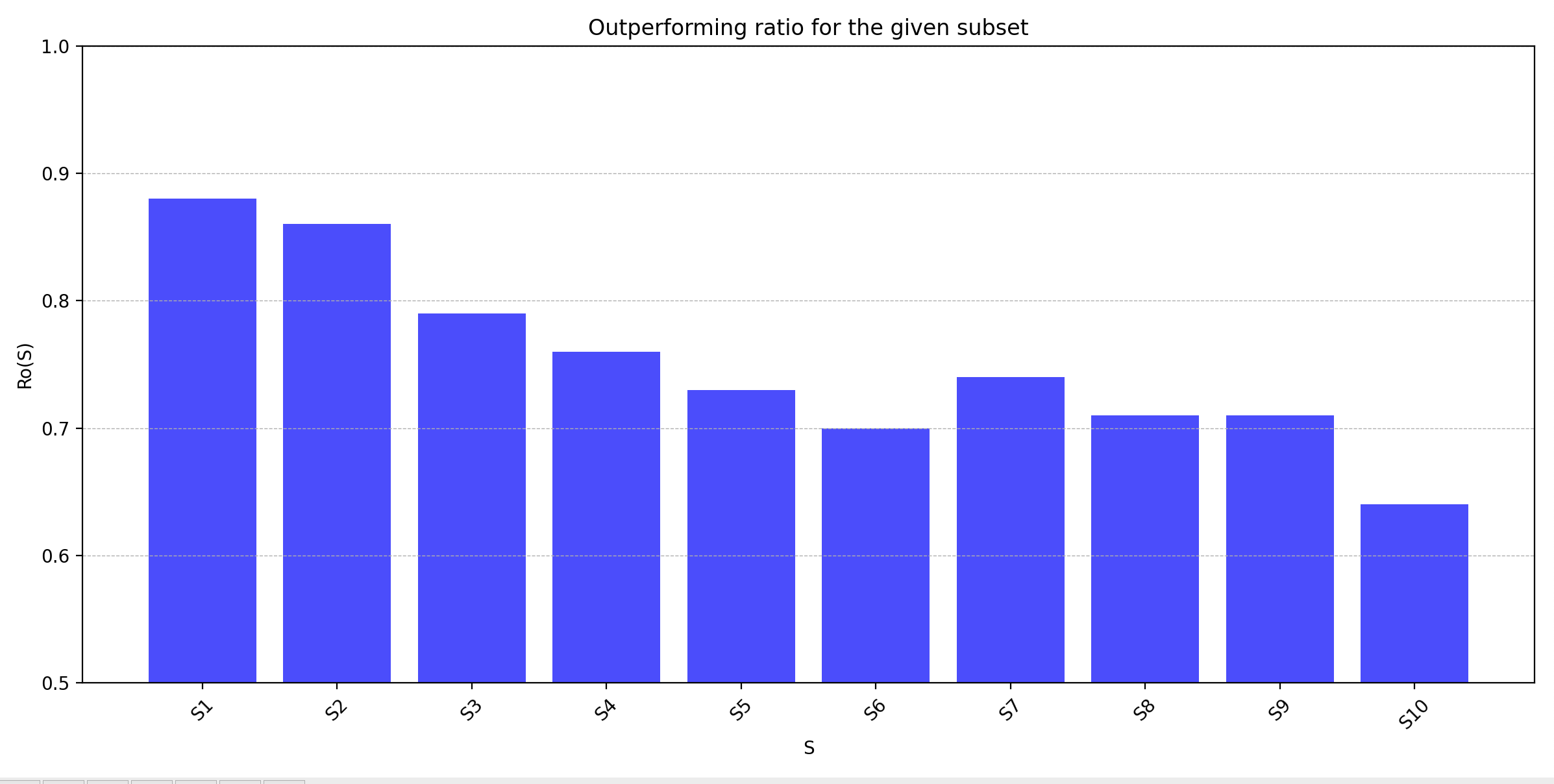
In Figure 9, we plot the ratio of outperforming pairs of concepts where \(S_1\) denotes the list of concept pairs with the highest \(CSR\) scores and \(S_{10}\) contains the pairs with the lowest \(CSR\) scores. As can be seen in Figure 9, we have the highest ratio of outperforming concept pairs for \(S_1\) with \(R_o(S_{1})=0.88\). The ratio falls as the \(CSR\) scores decrease. We see the lowest ratio \(R_o(S_{10})=0.64\) for \(S_{10}\) containing pairs with the lowest \(CSR\) scores.
If knowing the semantically referenced concepts has zero effect on the performance, the outperforming ratio is expected to be close to \(0.5\). However, our benchmark data set consists of concepts only within the Mathematics domain. Therefore all the concepts are related, and even knowing the least semantically referenced concept may have a positive effect on the student performance, which could be the reason for all the \(R_o\) values being above \(0.5\)
Overall, the decreasing \(R_o\) values for the \((A, B)\) pairs with lower \(CSR\) scores, and the increasing \(R_o\) values for the \((A, B)\) pairs with higher \(CSR\) scores demonstrate that student performances and \(CSR\) scores show correlation. To suppress the effect of the other hidden variables that can cause the performance differences between the students in \(TG\) and in \(CG\), we made sure that the students in \(CG\) solved only questions related to \(B\) and did not work on any questions from other concepts in the learning platform. This increased our confidence that the results of concept \(B\) were not influenced by knowledge or problem-solving skills from other concepts in the related domain. However, in order to take one step further and claim that \(CSR\) scores and student performances do not just have a correlation but also have a cause-and-effect relationship, further experiments should focus on collecting richer data with more student-related features such as age, current educational level, academic history or study material for the related concepts. By selecting students with similar features in \(TG\) and \(CG\), we can better control for these additional variables.
For reproducibility, we have posted all the data sets we extracted from the original benchmark data set on GitHub 10. The GitHub page includes all the Treatment Groups (\(TG\)), Control Groups (\(CG\)), concept pairs, textual descriptions (obtained from GPT-3), as well as the \(CSR\) scores.
6.3. Constructing and Evaluating MEKGs: Methodologies, Quality Metrics, and Efficiency Factors
In this section, we construct \(MEKG\)s using our ACE methodology and assess the quality of the resulting graphs. To evaluate the produced \(MEKG\)s, we use three different gold-standard datasets in our experiments. The first dataset is a \(KG\) from an e-learning platform called Metacademy, which specializes in topics related to machine learning11. This graph, which we refer to as Metacademy, has 141 nodes, each representing a concept from Machine Learning, Statistics, or Linear Algebra. Each concept has a short description provided by the experts of the Metacademy platform, and the directed paths represent the prerequisite relations among concepts. We remove the transitive edges from the Metacademy graph, turning it into a \(MEKG\). We also create our own gold-standard \(MEKG\) using our ACE web application. For that, we chose the Data Structures and Algorithms field, one of the core disciplines of computer science, and named the corresponding graph, consisting of 29 concepts, as DSA.
We use the gold-standard \(MEKG\)s with path recall and path precision as the quality metrics to compare two graphs. Let \(G_1\) and \(G_2\) represent two \(MEKG\)s that we want to compare. Let \(P_1\) be the set of all paths in \(G_1\) and \(P_2\) be the set of all paths in \(G_2\). We define path recall as:
\begin {equation} \label {eq:path-recall} PathRecall(G_1,G_2) = \frac {{|P_1 \cap P_2|}}{|P_1|} \end {equation}
Path precision is defined similarly:
\begin {equation} \label {eq:path-precision} PathPrecision(G_1,G_2) = \frac {{|P_1 \cap P_2|}}{|P_2|} \end {equation}
Assuming that the \(MEKG\) produced through the ACE methodology is denoted by \(MEKG_A\) and the gold-standard graph is denoted by \(MEKG_G\), to demonstrate the role of the expert on the quality of \(MEKG_A\), we plot the relative reduction of expert effort on the x-axis and plot the PathRecall(\(MEKG_G\), \(MEKG_A\)) on the y-axis. This way, we can observe the effect of reduced expert effort (i.e., reducing parameter \(t\)) on the path recall. We utilize 20 different values of \(t\) ranging from 5 to 100. We assume that the expert correctly identifies the prerequisite pairs in the top \(t\%\) of the concept pairs. Therefore, the path precision, which measures the fraction of paths in the compared \(MEKG\) that are also in the standard \(MEKG\), is always equal to 1, and we do not report it in the experiments. Furthermore, in order to observe the contribution of semantic reference over exact reference in the ranking process, we compute the prerequisite scores for the pairs twice, employing both \(CSR\) and \( CER\)-based approaches. Additionally, we use random ordering of the pairs as a baseline in which the \(t\) percentage of pairs is randomly presented to the expert, and the expert constructs the graph from those pairs.
| Dataset | # Concepts | # Unordered Pairs | # Direct Prerequisites | # Total Prerequisites |
|---|---|---|---|---|
| Metacademy | 141 | 9870 | 331 | 1586 |
| DSA | 29 | 406 | 55 | 111 |
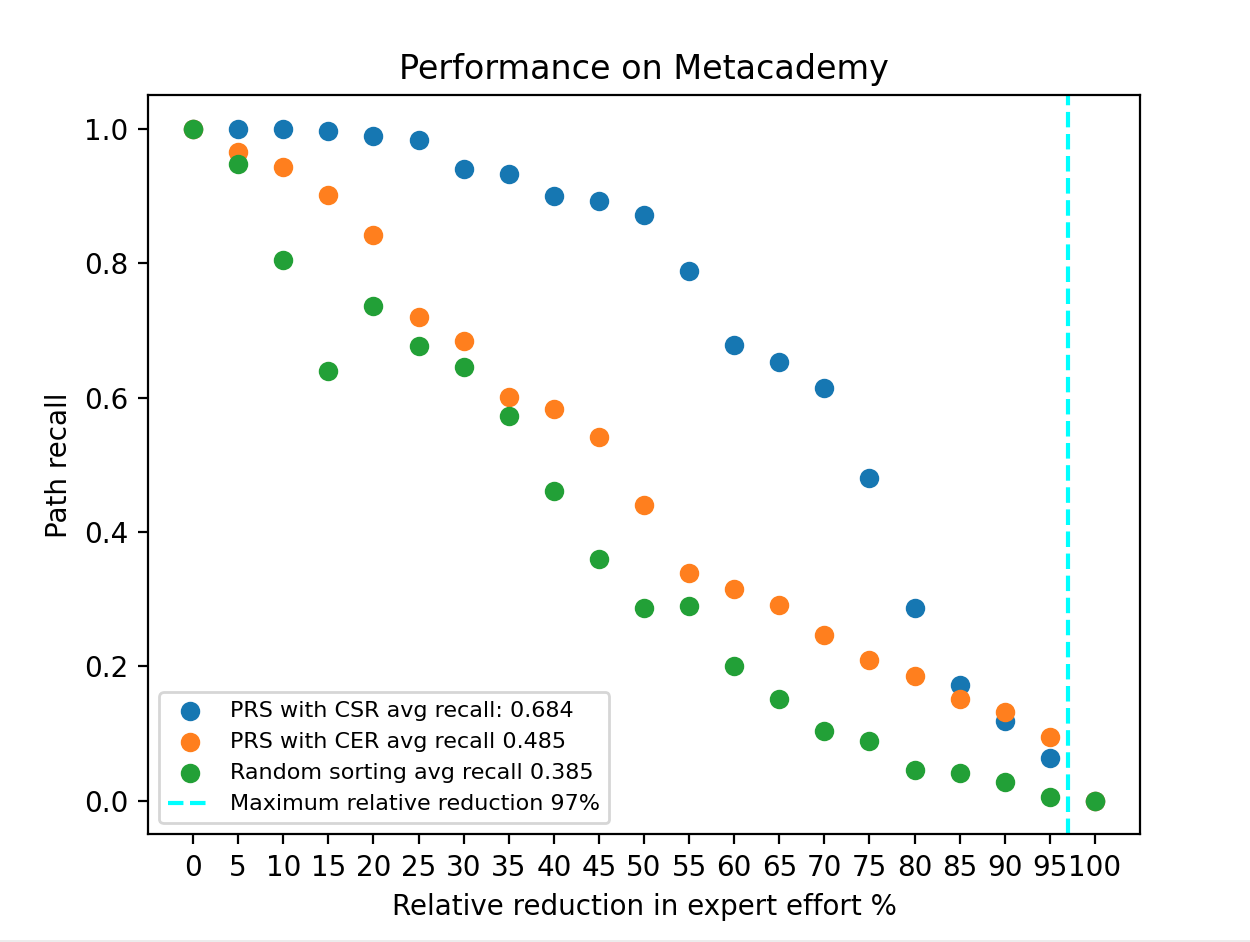
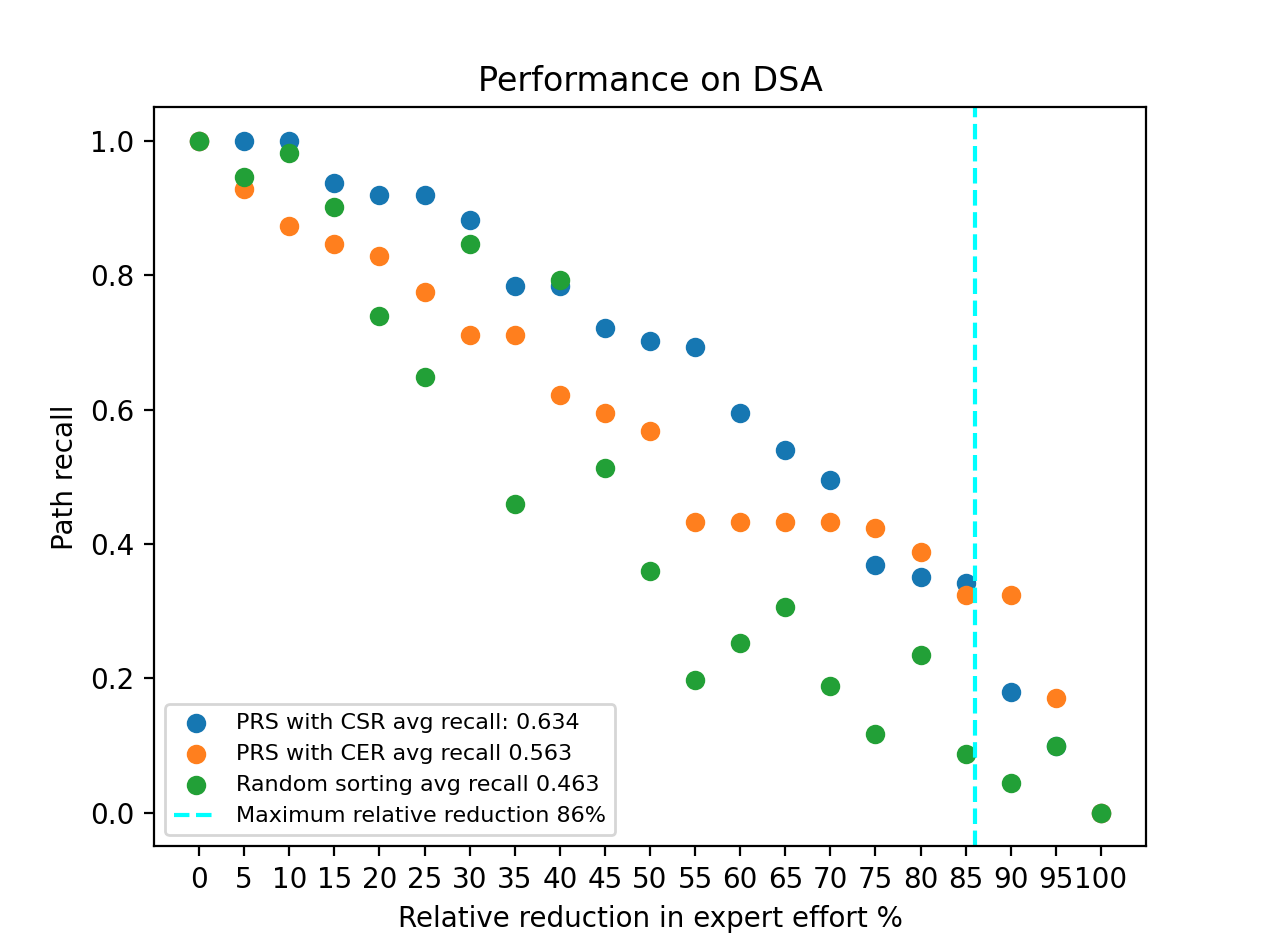
In Figure 10, we observe the path recall values on the y-axis for different values of relative expert effort reduction. For instance, when the relative expert effort reduction is 50%, the path recall for \(PRS\) with \(CSR\) is approximately 90%, indicating that our methodology produces a \(MEKG\) that is 90% similar to the Metacademy \(MEKG\) by letting the expert evaluate only half of the pairs. As expected, the lowest average recall value (0.385) belongs to random ordering. We also see that choosing semantic references over exact references increases average path recall from 0.485 to 0.684, which is a significant improvement. We also show the maximum relative reduction in the plot as a dashed line. This line corresponds to an x-axis value of 97, indicating that if the prerequisite ranking algorithm is perfect (every presented pair to the expert includes a prerequisite relation), then it would give a path recall value of 1 from 0 to 97 relative to the expert effort reduction. Therefore, while we can conclude that semantic references help us succeed in making our approach more feasible, there is still room for improvement. Similarly, in Figure 11, we observe that \(PRS\) with \(CSR\) mode achieves the best performance compared to the other approaches with a score of 0.634. Between the x-axis values (75-95), we see that both modes of \(PRS\) show almost equal performances. This can be because pairs with strong prerequisite relations tend to possess both exact and semantic references, while pairs with more subtle prerequisite relations typically display only semantic references. As the relative reduction in expert effort becomes more significant, only the topmost pairs are presented for evaluation. Consequently, both modes of \(PRS\) adequately capture these significant pairs. However, as the relative reduction in expert effort becomes less substantial, the \(CSR\) mode outperforms the other mode by effectively differentiating between subtle prerequisite pairs and non-prerequisite pairs.
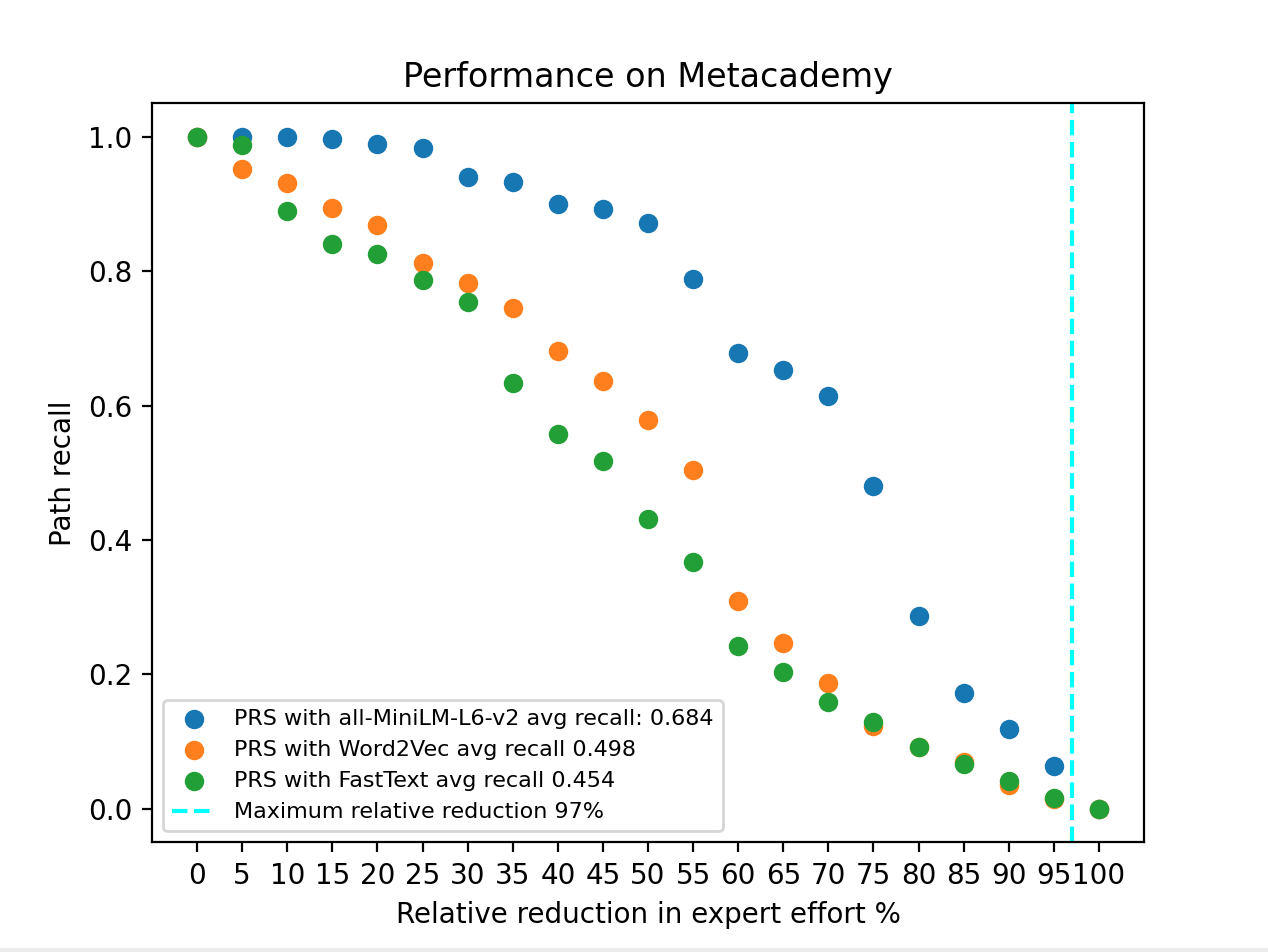
We also test the effect of the language model selection on the resulting quality of the constructed \(MEKG\). To do that, we construct 3 different \(MEKG\)s, one constructed with our main language model all-MiniLM-L6-v2 and the other two constructed using Word2Vec and Fasttext. For each constructed \(MEKG\), we calculate path recall for different relative reductions in expert effort and show the results in Figure 12. It can be observed from the figure that with all-MiniLM-L6-v2, we have higher path recall in the constructed \(MEKG\) for every \(t\) value between 5 to 95, indicating that it brings the top \(t\) percent of the sorted pairs to expert more accurately than the other language models.
There are three main factors affecting the runtime of our methodology: (1) the length of the concept descriptions, (2) The size of the concept set, and (3) The choice of the language model in \(CSR\) mode. To understand the impact of the first factor, we prepared five ranked lists for DSA with varying lengths and recorded the time taken to prepare each list, with the results detailed in Table 4. From the table, we observe that as the length of the concept descriptions increases, the runtime of our methodology also increases. This is expected as longer descriptions require more processing time to generate all pairwise prerequisite scores. For instance, when the length of the concept descriptions is 108 words, the runtime is 18 minutes, whereas for descriptions with a length of 1370, the runtime increases to 160 minutes.
| Avg length concept descriptions (# of words) | Runtime (in minutes) |
|---|---|
| 108 | 18 |
| 229 | 35 |
| 438 | 55 |
| 838 | 90 |
| 1370 | 160 |
| # concepts in subset MEKG | Runtime (in minutes) |
|---|---|
| 30 | 15 |
| 60 | 55 |
| 90 | 125 |
| 120 | 185 |
To assess the impact of the second factor, we use four different subsets of concepts from the Metacademy dataset and construct four different \(MEKG\)s with different numbers of concepts (Metacademy n=30, Metacademy n=60, Metacademy n=90 and Metacademy n=120). Each description has, on average, 78 words. From Table 5, it can be observed that as the number of concepts increases, the runtime of the methodology also increases in proportion.
Lastly, in order to understand the effect of the third factor, we present Table 6, which demonstrates the effects of the usage of different language models on the runtime. The three models analyzed are all-MiniLM-L6-v2, Word2Vec, and Fasttext. The table presents the runtimes in minutes for ranking all the pairwise prerequisites of 141 Metacademy concepts, each with an average description size of 78 words.
Based on the results presented in the table, it can be observed that the all-MiniLM-L6-v2 model has the longest runtime of 150 minutes. On the other hand, both Word2Vec and Fasttext have considerably shorter runtimes, with 12 minutes and 9 minutes, respectively. However, they exhibit lower path recall values, as shown in Figure 12.
| Utilized Word Embedding Model | Runtime (in minutes) |
|---|---|
| all-MiniLM-L6-v2 | 150 |
| Word2Vec | 12 |
| Fasttext | 9 |
These findings suggest that while all-MiniLM offers improved quality in the constructed \(MEKG\)s compared to Word2Vec and Fasttext, it constitutes the main bottleneck in the runtime of the methodology. Therefore, we consider the calculation of the similarity \(sim_{Cosine}(s_{ij},c_{k})\) between the concept description’s sentence (10-gram) and the concept’s name as the primary time-consuming process and count these operations as cost. If we have \(k\) number of sentences on average, then calculating \(CSR(c_{i},c_{k})\) requires \(k\) similarity operations. Since \(PRS\) computes the maximum of \(CSR(c_{i},c_{k})\) and \(CSR(c_{k},c_{i})\), we have \(2k \) operations for an unordered pair. The number of unordered pairs for \(n\) concepts is \(\frac {n \cdot (n-1)}{2}\); therefore we have \(k \cdot n(n-1)\) similarity operations for \(n\) number concepts. The dominating term is \(n^2\), and the time complexity of our prerequisite calculation is \(O(k \cdot n^2)\).
7. Conclusions and Future Work
Industrial adoptions of knowledge gave rise to the emergence of huge graph databases. For instance, DBpedia12 is updated with 22 billion new facts every month. The same trend can be realized in the educational domain, where educational knowledge graphs can be used to store and represent educational knowledge. In this paper, we propose an AI-assisted methodology to build Educational Knowledge Graphs (\(EKG\)) designed to show all the prerequisite relations among concepts within a domain. Considering the challenge of manual construction, we propose a methodology that can significantly reduce the expert’s workload. Moreover, we introduce a novel prerequisite scoring algorithm \(CSR\), which can assign unique prerequisite scores to concept pairs using the notion of semantic similarity. We also implemented our methodology in our web application and provided a framework for the experts who would like to create their own \(EKG\)s that can serve as a guide to students in their learning process. E-learning systems can also use these graphs as a database, and e-learning applications can use \(EKG\)s for various reasons, such as finding optimal learning paths for students or identifying concepts according to their difficulty level by looking at the number of incoming and outgoing edges on concepts. Given the scarcity of benchmark datasets for prerequisite identification in the literature (Roy et al., 2019), our framework can serve as a prerequisite labeled data generator. Future supervised models can use our framework to create training data for their models for prerequisite detection.
In future research, we plan to add other relations to \(EKG\)s, such as ‘subclass’ relations. These relations represent the hierarchy between concepts, where one concept is a subcategory or a specific instance of a broader concept, such as neural networks being a subclass of machine learning. This type of relation is often overlooked in publicly available prerequisite datasets. Moreover, in this work, we only demonstrated the transitivity property of the prerequisite relation to deduce new knowledge from the existing knowledge in our \(EKG\)s. However, incorporating new types of relations in our graphs can allow us to discover new types of rules for the introduced relations.
Our overall framework offers an alternative way to store, organize, and share domain knowledge using \(EKG\)s, which may lead to new research directions and pave the way for more efficient educational systems.
Acknowledgements
This work is partially funded by the TUBITAK Scientific and Technological Research Council of Turkey under the industrial PhD program of 2244 with Huawei Turkey Research and Development Center.
References
- Adorni, G., Alzetta, C., Koceva, F., Passalacqua, S., and Torre, I. 2019. Towards the identification of propaedeutic relations in textbooks. In Artificial Intelligence in Education, S. Isotani, E. Millán, A. Ogan, P. Hastings, B. McLaren, and R. Luckin, Eds. Springer International Publishing, Cham, 1–13.
- Aguiar, C. Z., Cury, D., and Zouaq, A. 2016. Automatic construction of concept maps from texts. In 4th International Conference on Concept Mapping. Springer, Tallinn, Estonia, 1–6.
- Aytekin, M. C., Räbiger, S., and Saygın, Y. 2020. Discovering the prerequisite relationships among instructional videos from subtitles. In Proceedings of the 13th International Conference on Educational Data Mining. International Educational Data Mining Society, Fully virtual conference, 569–573.
- Chen, P., Lu, Y., Zheng, V. W., Chen, X., and Yang, B. 2018. Knowedu: A system to construct knowledge graph for education. IEEE Access 6, 31553–31563.
- Chiou, C.-C., Tien, L.-C., and Lee, L.-T. 2015. Effects on learning of multimedia animation combined with multidimensional concept maps. Computers & Education 80, 211–223.
- Devlin, J., Chang, M.-W., Kenton, L., and Toutanova, K. 2019. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of NAACL-HLT. Association for Computational Linguistics, Minneapolis, Minnesota, USA, 4171–4186.
- Dong, L., Yang, N., Wang, W., Wei, F., Liu, X., Wang, Y., Gao, J., Zhou, M., and Hon, H.-W. 2019. Unified language model pre-training for natural language understanding and generation. In Proceedings of the 33rd International Conference on Neural Information Processing Systems. Curran Associates Inc., Red Hook, NY, USA.
- Furtado, P. G. F., Hirashima, T., and Hayashi, Y. 2019. Reducing cognitive load during closed concept map construction and consequences on reading comprehension and retention. IEEE Transactions on Learning Technologies 12, 3, 402–412.
- Gong, W., Smith, D., Wang, Z., Barton, C., Woodhead, S., Pawlowski, N., Jennings, J.,
and Zhang, C. 2022. Neurips competition instructions and guide: Causal insights for learning paths
in education.
https://arxiv.org/abs/2208.12610. - Hirashima, T., Yamasaki, K., Fukuda, H., and Funaoi, H. 2015. Framework of kit-build concept map for automatic diagnosis and its preliminary use. Research and Practice in Technology Enhanced Learning 10, 1, 1–21.
- Hogan, A., Blomqvist, E., Cochez, M., d’Amato, C., Melo, G. d., Gutierrez, C., Kirrane, S., Gayo, J. E. L., Navigli, R., Neumaier, S., et al. 2021. Knowledge graphs. ACM Computing Surveys (CSUR) 54, 4, 1–37.
- Jia, C., Shen, Y., Tang, Y., Sun, L., and Lu, W. 2021. Heterogeneous graph neural networks for concept prerequisite relation learning in educational data. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, K. Toutanova, A. Rumshisky, L. Zettlemoyer, D. Hakkani-Tur, I. Beltagy, S. Bethard, R. Cotterell, T. Chakraborty, and Y. Zhou, Eds. Association for Computational Linguistics, Online, 2036–2047.
- Lee, S., Park, Y., and Yoon, W. C. 2015. Burst analysis for automatic concept map creation with a single document. Expert Systems with Applications 42, 22, 8817–8829.
- Li, I., Fabbri, A. R., Tung, R. R., and Radev, D. R. 2019. What should I learn first: Introducing lecturebank for NLP education and prerequisite chain learning. Proceedings of the AAAI Conference on Artificial Intelligence 33, 01 (Jul.), 6674–6681.
- Liang, C., Wu, Z., Huang, W., and Giles, C. L. 2015. Measuring prerequisite relations among concepts. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Lisbon, Portugal, 1668–1674.
- Liang, C., Ye, J., Wu, Z., Pursel, B., and Giles, C. L. 2017. Recovering concept prerequisite relations from university course dependencies. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. AAAI’17. AAAI Press, 4786–4791.
- Liang, C., Ye, J., Zhao, H., Pursel, B., and Giles, C. L. 2019. Active learning of strict partial orders: A case study on concept prerequisite relations. In Proceedings of the 12th International Conference on Educational Data Mining (EDM 2019). International Educational Data Mining Society (IEDMS).
- Manrique, R., Pereira, B., and Mariño, O. 2019. Exploring knowledge graphs for the identification of concept prerequisites. Smart Learning Environments 6, 1, 1–18.
- Miaschi, A., Alzetta, C., Cardillo, F. A., and Dell’Orletta, F. 2019. Linguistically-driven strategy for concept prerequisites learning on Italian. In Proceedings of the Fourteenth Workshop on Innovative Use of NLP for Building Educational Applications. Association for Computational Linguistics, Florence, Italy, 285–295.
- Molontay, R., Horváth, N., Bergmann, J., Szekrényes, D., and Szabó, M. 2020. Characterizing curriculum prerequisite networks by a student flow approach. IEEE Transactions on Learning Technologies 13, 3, 491–501.
- Novak, J. D. 2010. Learning, creating, and using knowledge: Concept maps as facilitative tools in schools and corporations. Routledge, New York, NY, USA.
- Novak, J. D. and Cañas, A. J. 2006. The theory underlying concept maps and how to construct them. Florida Institute for Human and Machine Cognition 1, 2006–2001.
- Pan, L., Li, C., Li, J., and Tang, J. 2017. Prerequisite relation learning for concepts in MOOCs. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). Association for Computational Linguistics, Vancouver, Canada, 1447–1456.
- Pinandito, A., Prasetya, D. D., Hayashi, Y., and Hirashima, T. 2021. Design and development of semi-automatic concept map authoring support tool. Research and Practice in Technology Enhanced Learning 16, 1, 1–19.
- Roy, S., Madhyastha, M., Lawrence, S., and Rajan, V. 2019. Inferring concept prerequisite relations from online educational resources. Proceedings of the AAAI Conference on Artificial Intelligence 33, 01 (Jul.), 9589–9594.
- Sayyadiharikandeh, M., Gordon, J., Ambite, J.-L., and Lerman, K. 2019. Finding prerequisite relations using the wikipedia clickstream. In Companion Proceedings of The 2019 World Wide Web Conference. WWW ’19. Association for Computing Machinery, New York, NY, USA, 1240–1247.
- Shokrzadeh, Z., Feizi-Derakhshi, M.-R., Balafar, M.-A., and Bagherzadeh Mohasefi, J. 2024. Knowledge graph-based recommendation system enhanced by neural collaborative filtering and knowledge graph embedding. Ain Shams Engineering Journal 15, 1, 102263.
- Talukdar, P. and Cohen, W. 2012. Crowdsourced comprehension: Predicting prerequisite structure in Wikipedia. In Proceedings of the Seventh Workshop on Building Educational Applications Using NLP. Association for Computational Linguistics, Montréal, Canada, 307–315.
- Yang, C., Cui, H., Lu, J., Wang, S., Xu, R., Ma, W., Yu, Y., Yu, S., Kan, X., Ling, C., Fu, T.,
Zhao, L., Ho, J., and Wang, F. 2024. A review on knowledge graphs for healthcare: Resources,
applications, and promises.
https://arxiv.org/abs/2306.04802. - Yu, J., Wang, Y., Zhong, Q., Luo, G., Mao, Y., Sun, K., Feng, W., Xu, W., Cao, S., Zeng, K., Yao, Z., Hou, L., Lin, Y., Li, P., Zhou, J., Xu, B., Li, J., Tang, J., and Sun, M. 2021. Mooccubex: A large knowledge-centered repository for adaptive learning in moocs. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management. CIKM ’21. Association for Computing Machinery, New York, NY, USA, 4643–4652.
- Zhang, J., Lan, H., Yang, X., Zhang, S., Song, W., and Peng, Z. 2022. Weakly supervised setting for learning concept prerequisite relations using multi-head attention variational graph auto-encoders. Knowledge-Based Systems 247, 108689.
1https://github.com/cemaytekin/EKG-Dataset
2http://aytekincem.pythonanywhere.com/
3https://en.wikipedia.org/wiki/Google_Knowledge_Graph
4https://radimrehurek.com/gensim/models/word2vec.html
5https://www.microsoft.com/en-us/research/publication/
6https://huggingface.co/sentence-transformers/all-MiniLM-L6-v2
7https://github.com/suderoy/PREREQ-IAAI-19
8https://openai.com/blog/gpt-3-apps/
9https://www.llama.com/llama-downloads
10https://github.com/cemaytekin/EKG-Dataset