Abstract

This paper describes how to discover simple logistic regression models that outperform more complex approaches such as Deep Knowledge Tracing (DKT) and Self-Attentive Knowledge Tracing (SAKT). Creating student models is done either by expert selection of the appropriate terms, beginning with models as simple as Item Response Theory (IRT) or Additive Factors Model (AFM) or with more “black box” approaches like DKT, in which the model discovers student features. We demonstrate how feature search approaches (i.e., stepwise selection or Least Absolute Shrinkage and Selection Operator (LASSO)) can discover superior models that are explainable. Such automatic methods of model creation offer the possibility of better student models with reduced complexity and better fit, in addition to relieving experts from the burden of searching for better models by hand with possible human error. Our new functions are part of the preexisting R package Logistic Knowledge Tracing (LKT). We demonstrate our search methods with three datasets in which research-supported features (e.g., counts of success, elapsed time, recent performance) are computed at multiple levels (student, knowledge component (KC), item) and input to stepwise regression and LASSO methods to discover the best-fitting regression models. The approach was intended to balance accuracy and explainability. However, somewhat surprisingly, both stepwise regression and LASSO found regression models that were both simpler and more accurate than DKT, SAKT, and Interpretable Knowledge Tracing (IKT) in all datasets, typically requiring multiple orders of magnitude fewer parameters than alternatives.

Keywords

Introduction

Adaptive learning technology requires estimating a student’s learning in order to make decisions about how to interact with the student. The general assumption is that a model of students provides values (e.g., probability estimates typically) that are used to make decisions on pedagogy, the most common decisions being about when or whether to give practice and also how much practice to give (e.g., has the student mastered the proficiency; Pavlik Jr. et al., 2013). While pursuing a higher model fit presents challenges, an equally pressing issue is the rising complexity associated with handcrafting new models for different content areas and types of learning technology.

This paper describes a tool to build logistic regression models automatically from student data. We focus on finding models that are explainable and parsimonious for various reasons. One reason is due to the need for open learner models to provide interpretation of the student data, e.g., in a student dashboard, which means that there are benefits if it is scrutable, can be made cooperative, and is editable (Conati et al., 2018). Complex models make these things more difficult to achieve. Trust is another advantage of explainable systems (Khosravi et al., 2022), which can increase stakeholder adoption. Moreover, pursuing ever-more complex models does not merely make it difficult to achieve explainability; it also erects a formidable barrier to entry for practitioners, requiring an intricate set of skills and domain-specific knowledge.

A common practice in student modeling research is choosing models based on fit statistics such as AUC and RMSE. However, the practical benefits of going from an AUC of .85 to .88 (for instance) may be close to zero, depending on how the model is used. If it is being used for reporting proficiency to a dashboard (e.g., in binary terms such as mastered or not), both models may come to the same conclusions. In adaptive instructional systems, whether the better fitting model changes practice sequences depends on the decision rules utilizing the model predictions. Frequently, the same recommended practice sequences will be recommended from both models. In short, there are dramatically diminishing returns from improving model fit, and if the improvement reduces explainability, it may be unjustified. The present work addresses this tension between optimal model fits and practical considerations.

Unfortunately, because student models differ by content area and the type of learning technology, it often seems necessary to handcraft new models to maximize model accuracy (Cen et al., 2006; Chi et al., 2011; Galyardt and Goldin, 2015; Gervet et al., 2020; Gong et al., 2011; Pavlik Jr. et al., 2009; Schmucker et al., 2022; Yudelson et al., 2011). Handcrafting has created a parade of alternatives such that a huge amount of researcher knowledge is necessary before a practitioner can easily transfer these methods to new systems. The researcher must be an expert in quantitative methods of knowledge tracing, have a deep understanding of the domain, and be adept in the learning science principles important in that domain (repetition, spacing, forgetting, and similar principles.). In addition to these basic technical skills, there are the complexities of model building itself, such as overfitting and the need for generalization. This base knowledge necessary for model creation creates a long learning curve.

We suppose that the long learning curve in our area can be solved by building better tools to build models. We have been using LKT, which subsumes many prior logistic models by providing a flexible model-building framework in R (Pavlik et al., 2021). However, although LKT enables the use of many predictive features, it did not select features for the user. The present work illustrates its new functionality to select a subset of features for the user automatically. The idea of having a large feature space that can be searched for interactive features to produce different previously studied models (like AFM and PFA) is less well-studied but not entirely novel (Vie and Kashima, 2019).

With the purported excellent model fits of recent deep learning models, some readers will see this prior research as a dead end that people need to move away from, but from these authors’ perspective, that is unlikely to be the case. Deep learning student modeling (e.g., Piech et al., 2015) has been around for several years but can be more complicated to implement within adaptive practice systems than regression and harder to interpret model parameters and errors. New deep-learning models can fit well but do not seem to fit reliably better than simpler alternatives (Gervet et al., 2020). The complexity may be unwarranted for applications in many cases unless there is some demonstration that these models can predict student knowledge better than simpler methods like logistic regression. To help establish that the gains for using more complex methods are small, we compare three complex methods with logistic regression in the LKT package.

If logistic regression can compete in terms of fit, it becomes important to emphasize that the simplicity of regression means that software developers and educational content developers can incorporate student models of astounding power using basic algebra. Incorporating such models as pedagogical decision-makers in educational software is relatively straightforward and well-described. So, in this paper, we also look more deeply at one of the remaining stumbling blocks in the more widespread use of logistic regression to trace student learning — choosing features.

While the LKT R package allows the application of more than 30 features, it did not previously provide any direction on how to choose these features for the components (e.g., KCs, students, items) of the data. Choosing such component/feature pairs is also difficult for an expert since despite an expert perhaps understanding the palette of possible features, given 3 levels of components (e.g., as in BestLR below, with student, items, and KCs), there can be more than 90 possible choices to add to a model (assuming we search across all 30 features for each component).

With such a large palette for each of multiple terms in the regression, it is understandable that we have very coefficient-heavy models like BestLR being proposed in the literature (Gervet et al., 2020) since it is very hard to exclude all the possibilities to find one logistic regression model to rule them all. Best LR is formulated with the following equation, where α is the student ability, δ is item difficulty, φ is the function log(x+1), β is the KC difficulty, and γ and ρ capture the effect of prior success (c counts) and failures (f counts) for the KC. The function $\phi$ scales those counts according to $\phi(x) = \log(1 + x)$. The σ (sigmoid) function transforms the linear measure to the logistic prediction probability. Here, s indexes the student, and t predicted trial, and $\mathbf{x}$ indexes all the prior data from the student. The left side of the equation says we are predicting the correctness of each trial (a=1) conditional on the question ($q_{s,t + 1})$ given the student and all the prior data for that student. Note “α” and “a” represent different quantities. So, then the linear input to the sigmoid transformation includes student ability, item difficulty, log of 1+ prior success for student, log of 1+ prior failures for student, sum of the difficulty of all KCs in the item, log of 1+ prior success for each KC and log of 1+ prior failures for each KC.

$BestLR\left( a_{s,t + 1} = 1 \middle| q_{s,t + 1},\mathbf{x}_{s,1:t} \right) = \ \sigma(\alpha_{s} - \delta_{q_{s,t + 1}}\ + \phi(c_{s})\ + \phi\left( f_{s} \right) + \sum_{{k\epsilon KC(q}_{s,t + 1})}^{}\beta_{k} + \gamma_{k}$ϕ$(c_{s,k})\ + \rho_{k}\phi\left( f_{s,k}) \right)$

It is unclear if such complexity in BestLR is warranted. To address this problem in the complexity and potential inefficiency of logistic regression model creation generally, we describe and test our tool for stepwise and LASSO student model search in LKT. For the expert, these methods will save either the need to use “cookie-cutter” models that they know (but that may not be appropriate) or the countless hours of manual search that is often necessary when trying to understand modeling in a new domain. For the practitioner, this LKT package will allow the fast creation of models tailored to multiple purposes and domains. For the student modeler, the package provides a way to begin building models quickly and with sufficient feedback so as to think deeply about the functioning of those models. The example vignette in the LKT R package shows many examples from this paper.

Comparison Methods

In this journal version of our 2023 Educational Data Mining Conference Best Paper, we sought to improve our analysis methods by adding various enhancements to our comparisons. The three main enhancements were to carefully crossvalidate our results to ensure they were not the result of overfitting and to compare our methods vs. a variety of powerful alternatives that have recently shown their ability to produce very good results. Finally, we added another dataset, ASSISTments2012, an order of magnitude larger than previously used. These additions provide a richer sense of the advantages of LKT modeling.

To further contextualize the utility of logistic regression models, we will compare their performance with other complex modeling approaches, assessing the tradeoffs involved. The student-stratified crossvalidation we apply to these models is a rigorous test of their generalizability and allows us to make clearer comparisons with Deep Knowledge Tracing (DKT), Self-Aware Knowledge Tracing (SAKT), and Interpretable Knowledge Tracing (IKT). These alternative methods were chosen based on their strong performance in the recent literature (Gervet et al., 2020; Minn et al., 2022; Pandey and Karypis, 2019; Xiong et al., 2016). While we will argue that these alternatives are harder to explain (Khosravi et al., 2022), we would also argue that there is a tradeoff between explainability and effectiveness, so perhaps less explainable student models might be worth adopting should their accuracy well exceed easy to explain models.

Methods

Stepwise LKT

Stepwise LKT is simply the stepwise method applied to the LKT model fitting function. In the buildLKTModel R function, the user may set the objective function (BIC, AIC, AUC, R2, or RMSE). However, these metrics behave quite similarly in our testing except for BIC, which corrects heavily for the potential of overfitting due to high parameter counts. The user may specify a forward or backward search or alternate between forward and backward (bidirectional search). The user also has control over the initial features and components in the model, allowing the exploration of theoretical hypotheses for completed models and optimizing those models. For example, in our tests, we illustrate starting with the BestLR model and then allowing the algorithm to simplify the model while simultaneously adding a key new predictor. The user can also specify the forward and backward step size needed for the objective function (fit statistic), which is also chosen.

Stepwise Crossvalidation

As shown in the captions for the results, this version of the paper has full crossvalidation of results. In the case of the stepwise procedure, this student-stratified crossvalidation validates the entire process by ensuring no leakage of any model information between the models found for the held-out data in each iteration. We do the entire stepwise search process, independently finding the model terms, coefficients, and nonlinear feature parameters for the training folds and then testing how well that final model fits the held-out fold. This crossvalidation is implemented by a change in the main LKT R function that allows it to fit a model for a subset of the data, yet where it still computes and outputs the features for the entire dataset, allowing the model to be fit for the held-out data following the LKT function call (Pavlik Jr and Eglington, 2021). The 5-folds used for each of the three datasets were also used for all subsequent fits for LKT-LASSO SAKT, IKT, and DKT unless otherwise specified. The data preparation code is also shared in the R package.

LKT-LASSO

An alternative approach to stepwise regression is LASSO regression, a form of regularization. In this method, a penalty term is added to the loss function equal to the sum of the absolute values of the coefficients times a scalar lambda. This penalty term may result in the best-fitting model having fewer features if they are correlated. Larger lambda values will result in fewer features. A common method to use this approach is to attempt a large number of potential lambda values and choose the value with the best cross-validated performance. In the present case, we are particularly concerned with finding interpretable models that are easier to implement, so larger values with slightly worse performance may be preferred. To evaluate the resultant models from LKT-LASSO, we began by using the glmnet R package to fit both datasets with 100 values starting at the lowest value that would reduce all coefficients to zero (the maximum lambda) decreasing in increments of .001 (e.g., the default strategy with glmnet; Friedman et al., 2010). This method allowed us to evaluate the stability of the candidate lambda values. Subsequent model fitting and analyses used specific lambdas to evaluate the fit and interpretability of LASSO models with varying levels of complexity to determine the usefulness of LASSO compared to stepwise regression. An important distinction between LASSO and the stepwise approach employed in this work is that the coefficients for individual KCs may be dropped for LASSO. For instance, if two different KCs are essentially redundant, a LASSO model may reduce a coefficient for one of them to zero if the lambda value is large enough. In contrast, the stepwise regression approach we employed treats the KC model as a single feature; either it is included, or it is not.

For nonlinear features logitdec, propdec, and recency, features were generated with parameters from .1 to 1 in .1 increments (e.g., propdec with decay parameters .1, .2, up to 1). All the resultant features were included in the LKT-LASSO models to allow us to evaluate which parameter values remained and whether more than one was beneficial.

DKT

Deep Knowledge Tracing (DKT) is a recurrent neural network approach to knowledge tracing first introduced by Piech et al. (2015). It is a Long Short Term Memory (LSTM) variant of a recurrent neural network architecture initially developed to overcome the vanishing gradient problem (Hochreiter and Schmidhuber, 1997). Knowledge states and temporal dynamics are intended to be represented in large neural layers. More recently, DKT was shown to perform well on some datasets (Gervet et al., 2020) when compared against BKT, IRT, and particular implementations of logistic regression (termed ‘BestLR’). DKT had the highest AUC on 4 of 9 datasets. Logistic regression, feedforward neural networks, and SAKT won or tied on the remaining datasets. Notably, DKT was rarely far behind the winning model (Gervet et al., 2020). For more details about DKT architecture and implementation, see Xiong et al. (2016). DKT was fit to the present datasets using the code provided by Gervet et al. (2020), https://github.com/theophilegervet/learner-performance-prediction.

SAKT

Self-Attentive Knowledge Tracing (SAKT) model is a transformer architecture originally intended to improve upon prior approaches like DKT by weighting prior practice on KCs according to their predictiveness for the present practice item. In other words, not all prior practice was considered equally relevant. This approach was intended to overcome data sparsity issues that can limit models like DKT. In some cases, SAKT was shown to fit similarly (Gervet et al., 2020) or better than DKT (Pandey and Karypis, 2019). Analyses of the attentional weights of the model by the original authors indicated that the weights could be used to interpret inferred relations among the KCs. SAKT was fit to the present datasets using the code provided by Gervet et al. (2020), https://github.com/theophilegervet/learner-performance-prediction.

IKT

Interpretable Knowledge Tracing (IKT) is an explicit attempt to make a knowledge tracing model that is accurate and interpretable (Minn et al., 2022). This interpretability was operationalized as partitioning the contributions of problem difficulty, skill mastery, and student-level “ability profile” (intended to track learning transfer ability) into separate input variables in a Tree-Augmented Naive Bayes classifier (TAN). Problem difficulty was estimated by grouping individual practice items into ordered bins from 1-10 according to difficulty, enabling simpler fitting of their tree structure. Skill mastery was estimated using per-skill BKT models. Ability profiles were estimated by first dividing prior student interactions into time intervals. Students were clustered into ability groups to represent their learning ability over a time interval. This ability was computed across skills, thus allowing learning transfer to varying degrees. This approach also allows simple ablation of the model to ascertain the source of model accuracy (e.g., removing the problem difficulty feature is straightforward). IKT is relatively simple compared with contemporary knowledge tracing models while outperforming several of them (including DKT) on multiple datasets. However, when we fit IKT using code by the authors, the first trials of students in test folds appeared to be removed during the feature generation process (which can also be seen in their example data on their GitHub). This data preparation step is likely to have some effect on the model's results, albeit small. Despite some ambiguity about why initial trials are dropped when using their code, we decided to still include the model due to its impressive performance and relative simplicity.

Datasets

Cloze practice

The statistics cloze dataset included 58,316 observations from 478 participants who learned statistical concepts by reading sentences and filling in missing words. Participants were adults recruited from Amazon Mechanical Turk. There were 144 KCs in the dataset, derived from 36 sentences, each with one of four possible words missing (cloze items). The number of times specific cloze items were presented and the temporal spacing between presentations (narrow, medium, or wide) was manipulated. The post-practice test (filling in missing words) could be after two minutes, one day, or three days (manipulated between students). Data is available at https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=5513. The preprocessing code for this dataset and the other two used in this paper are available as part of the LKT R package documentation here: https://cran.r-project.org/web/packages/LKT/vignettes/Examples.html.

The stimuli type, manipulation of spacing, repetition of KCs and items, and multiple-day delays made this dataset appropriate for evaluating model fit to well-known patterns in human learning data (e.g., substantial forgetting across delays, benefits of spacing). As components, we choose to use the IDs for the student (Anon.Student.Id), sentence itself (KC..Cluster, 32 levels due to each sentence having two feedback conditions which we do not investigate here), specific items (KC.Default.) and the response word (CF..Correct.Answer.). KC..Default. (items) and CF..Correct.Answer. (answers) had a good deal of overlap since there were 72 items with 64 different answers. Here are two examples of these items, "The standard deviation is a __________ that describes typical variability for a set of observations.", and "Standard deviation is the __________ of the variance, also known as root mean squared error."

MATHia Cognitive Tutor equation solving

The MATHia dataset included 119,379 transactions from 500 students from the unit Modeling Two-Step Expressions for the 2019-2020 school year. We used the student (Anon.Student.Id), MATHia assigned skills (KC..MATHia.), and Problem.Name as the item. This decision meant that our item parameter was distributed across the steps in the problems. There were nine KCs and 99 problems. For simplicity, we chose not to use the unique steps as an item in our models. This dataset included skills such as “write expression negative slope” and “enter given, reading numerals”. Data is available at https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=4845.

ASSISTments 2012-2013 Dataset

The ASSISTments system is an online platform designed to provide immediate, formative feedback to students as they engage in problem-solving activities, primarily in mathematics (Feng et al., 2009). It serves dual purposes: it assists students by offering hints and guidance while they work on problems, and it simultaneously assesses their performance, thereby providing valuable data for educators. We used the 2012-2013 data available online and used by a recent paper on IKT (Minn et al., 2022). We attempted to process the data identically to this paper, but their code was unavailable, and we got an N of observations of 2540455 compared to their paper, which used 2506769. For the stepwise model, we used a subset of 5% of this data, 124,176 rows. We used skill, problem-type, and type columns in the data as potential knowledge components in our search. We did not use problem_id since the models ran too slowly for search, but then we applied a data-compression method to group the problem_ids and relabel them as similar to the IKT model technique, see our discussion of this issue below. As noted above, the full dataset was 2540455 rows after cleaning. Our cleaning code (available in the LKT package vignette) removed blank skills, repeated rows, cases where there was no outcome for correctness and then filtered for users with 20 more rows. Data is available at https://sites.google.com/site/assistmentsdata/datasets/2012-13-school-data-with-affect.

Results

Stepwise LKT

For the stepwise method, it is possible to use any collection of features as a “start” model that is subsequently added to and subtracted from. Using different starts helps us understand how the method can have problems with local minima but also helps us see that these problems are rather minimal as the different starts converge on similar results. At the same time, showing how the method improves upon “stock” models is an important part of the demonstration, showing that these “stock” models are not found to be particularly precise, and we might question whether better local minima are an improvement.

We choose to use AFM (Cen et al., 2006) and BestLR (Gervet et al., 2020) models as starting points, in addition to using an empty start (which included a global intercept to account for the grand mean of performance, as did all our models without explicit intercepts). AFM and BestLR starts are interesting since they illustrate the advantages of using the search method by arriving at models that fit better or equivalently with fewer parameters. Furthermore, using these start points allows us to show that these canonical models are not even local minima, which highlights how our methods are useful. If these models are particularly strong, it should not be possible to add terms to them, and the current terms should not be dropped.

Using these starts, we search over a preset group of features that are meant to be “complete enough” to produce interesting, relevant results and go beyond BestLR features (which it includes) to include some of the simplest and most predictive nonlinear features we have developed in other work (Pavlik et al., 2021).

We used several features, which we crossed with all the possible components (listed below) for each dataset. A $ indicates that the feature is fit with one coefficient per level of the component (e.g., one coefficient for each KC, student, or item). Intercept (a fixed coefficient for each level of the feature) does not require the $ notation since it is always fit this way. In contrast, without a $ indicates that all levels of the KC behave the same, so, for example, lineafm$ for the student means that there would be a continuous linear increase in performance for each trial for each student, with a different rate for each student.

We choose a limited set of likely features from the LKT software to search across. These included:

• Intercept–one coefficient for each level of the component factor
• Lineafm–one coefficient to characterize the linear change with each repletion of the component.
• Logafm–one coefficient to characterize the logarithmic change with each repetition for each level of the component. One is added to prior repetitions.
• Linesuc–one coefficient to characterize the linear change with each successful repetition for each level of the component.
• Linefail–one coefficient to characterize the linear change with each failed repetition for each level of the component.
• Logsuc–one coefficient to characterize the logarithmic change with each successful repetition for each level of the component. One is added to prior repetitions.
• Logfail–one coefficient to characterize the logarithmic change with each failed repetition for each level of the component. One is added to prior repetitions.
• Logitdec–one coefficient to characterize the logit of prior success and failures for the component (seeded with one success and one failures resulting in a start value of 0, e.g., log(.5/.5)=0). It uses nonlinear exponential decay to weight priors according to how far they are back in the sequence for the component traced.
• Propdec–one coefficient to characterize the probability of prior success and failures for the component (seeded with 1 success and 2 failures resulting in a start value of 0, e.g., .5/1)=.5). Uses a nonlinear exponential decay to weight prior success and failures according to how far they are back in the sequence for the component traced.
• Recency–one coefficient to characterize the influence of the recency of the previous repetition only, where t is the time since the prior repetition at the time of the new prediction and d characterizes nonlinear decay. The value is computed as t^-d.
• Logsuc$–like logsuc above, except one coefficient is added per level of the component (e.g., different effects for each KC or item)
• Logfail$–like logfail above, except one coefficient is added per level of the component (e.g., different effects for each KC or item)

Cloze practice

For the AFM start, the final model is specified in feature(component) notation; see equation below.

$$intercept(CF..Correct.Answer.) + recency(KC..Default.) + logsuc(CF..Correct.Answer.) + \ propdec(Anon.Student.Id)$$

See Table 1 and Figure 1 for the step actions that led to this final model. Note that in these figures, the results for the 5^th fold are displayed, and the values for 3 fit statistics (AUC, R2, and RMSE) are shown in the caption. As we can see, the cloze models crossvalidate well, perhaps due to the conservative 500 BIC threshold needed for the inclusion of the features in the model.

.

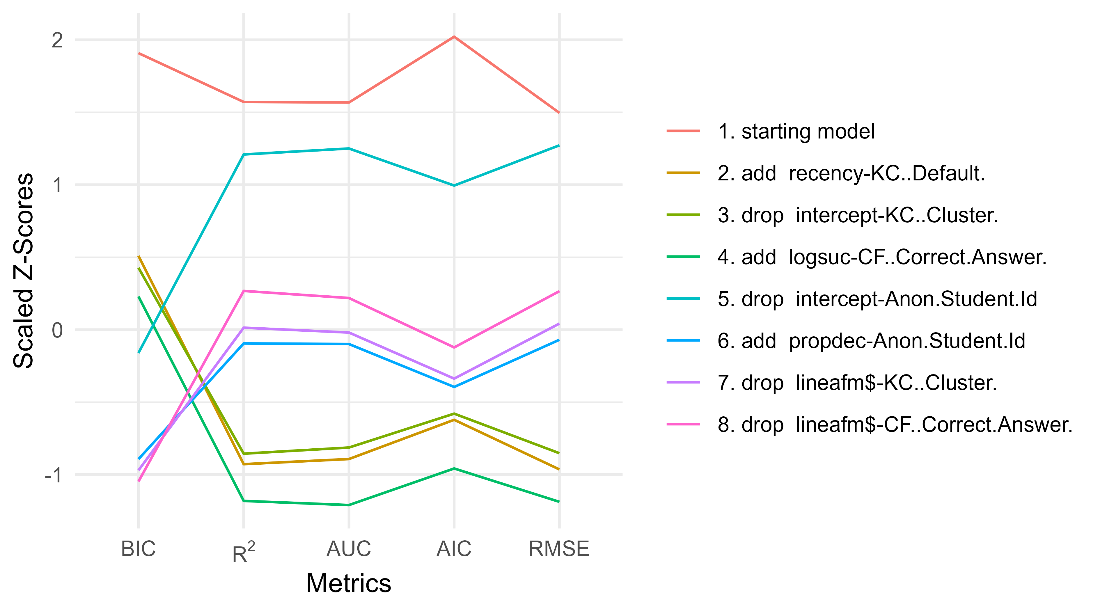
For the BestLR start, the final model is specified in feature(component) notation; see the equation below.

$$logsuc(Anon.Student.Id.) + logfail(Anon.Student.Id.) + intercept\ (CF..Correct.Answer.) + logsuc\$(CF..Correct.Answer.) + recency(KC.Default)$$

See Table 2 and Figure 2 for the step actions that led to this final model.

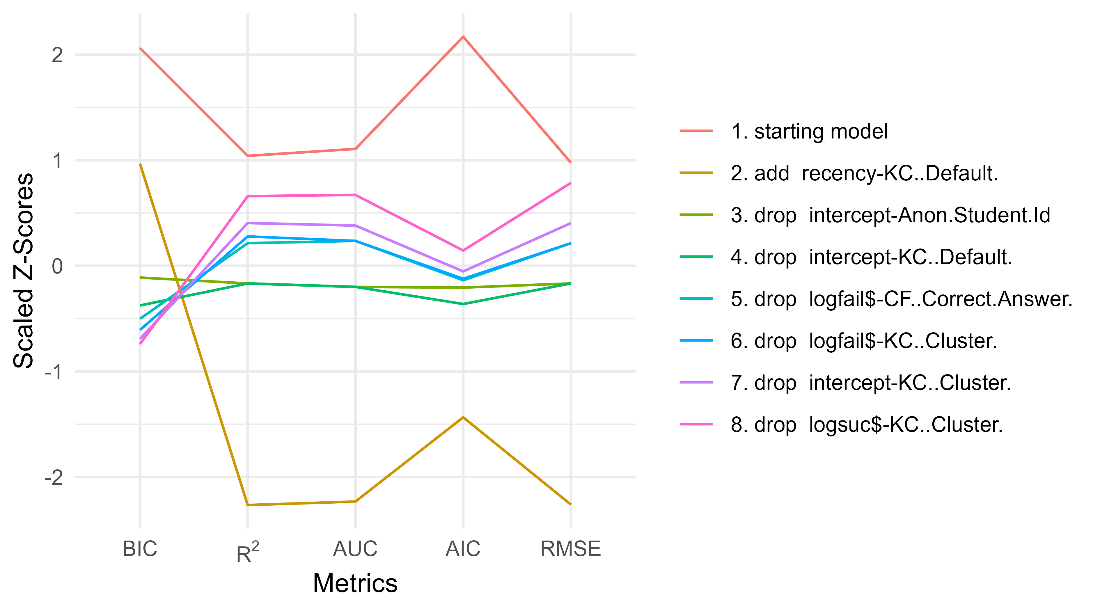
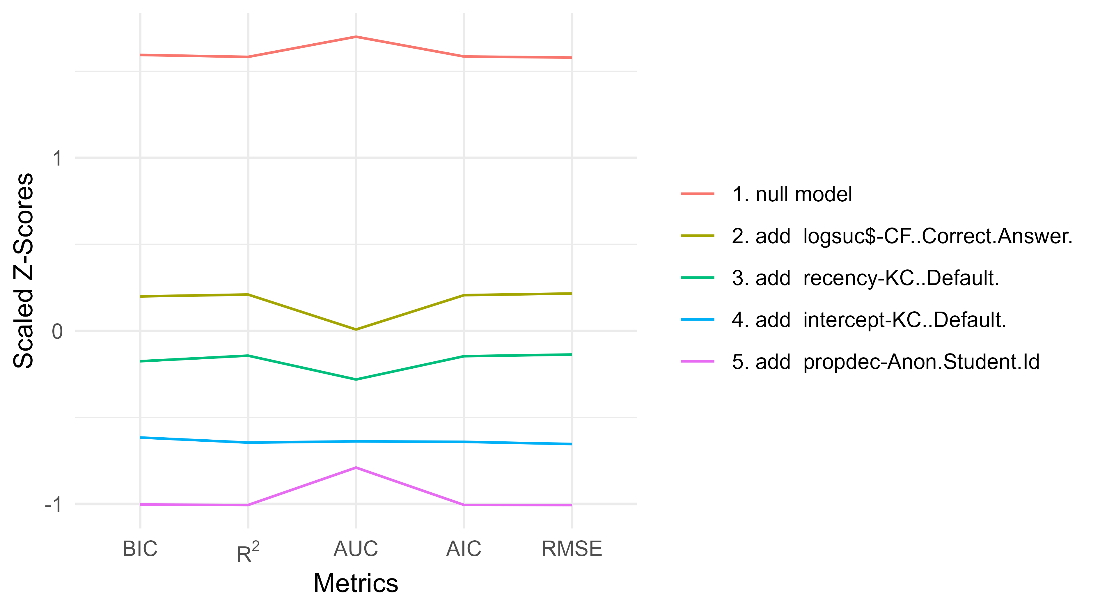
For the empty start, the final model is specified in feature(component) notation; see the equation below.

$$logsuc\$(CF..Correct.Answer.) + recency(KC..Default.) + intercept(KC..Default.) + propdec(Anon.Student.Id)$$

See Table 3 and Figure 3 for the step actions that led to this final model.

MATHia Cognitive Tutor equation solving

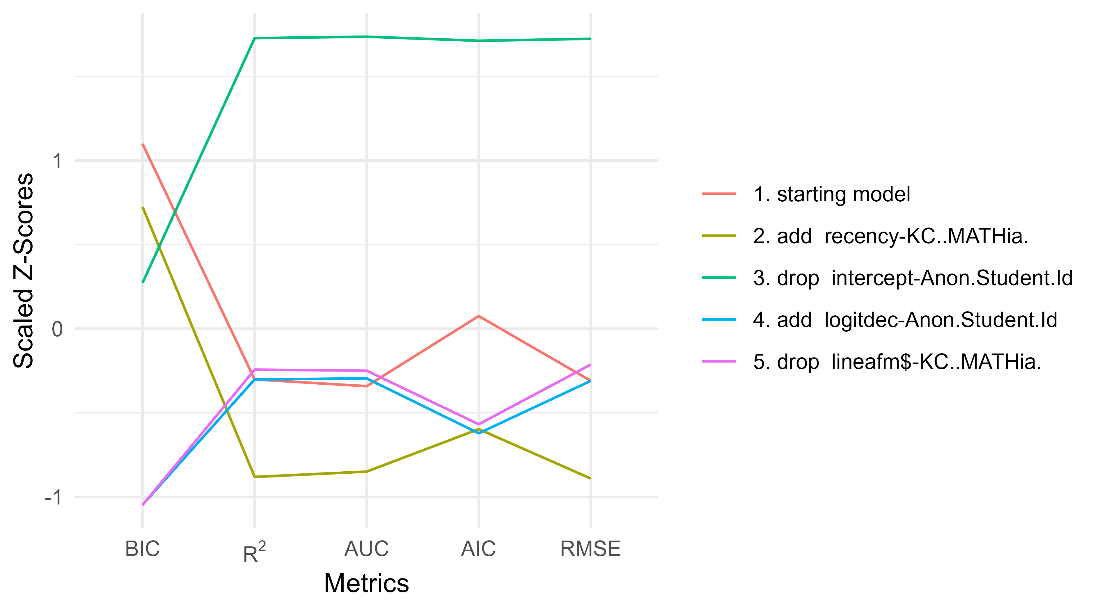
For the AFM start, the final model is specified in feature(component) notation; see the equation below.

$$logitdec(Anon.Student.Id) + recency(KC..MATHia.) + intercept(KC..MATHia.)$$

See Table 4 and Figure 4 for the step actions that led to this final model.

For the BestLR start, the final model is specified in feature(component) notation; see the equation below.

$$logfail(Anon.Student.Id) + logsuc(Anon.Student.Id) + intercept(KC..MATHia.) + recency(KC..MATHia.) + recency(Problem.Name) + linesuc(Problem.Name)$$

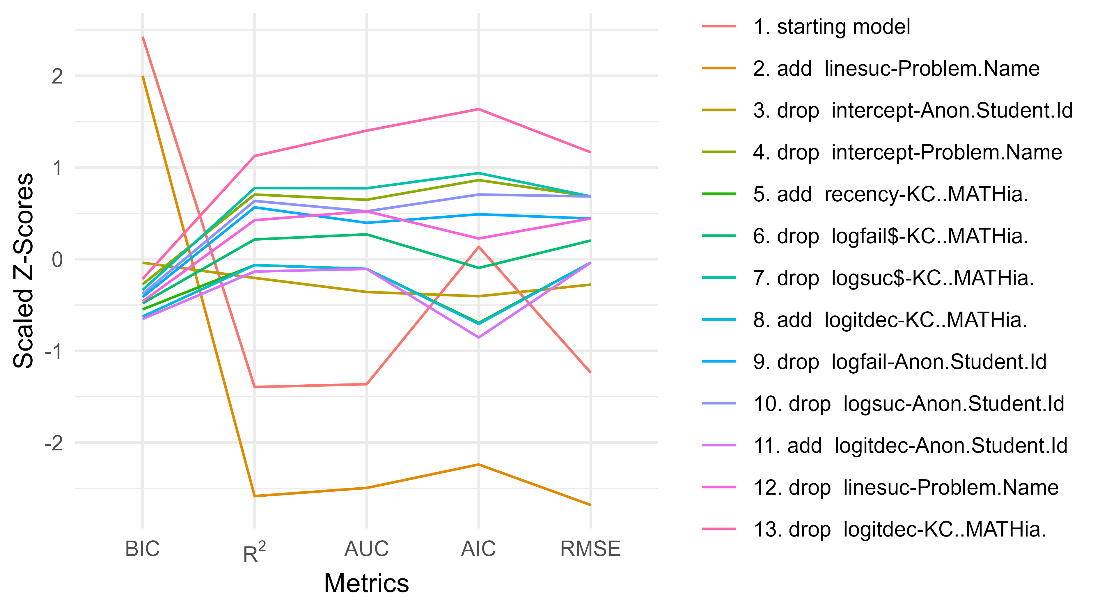
See Table 5 and Figure 5 for the step actions that led to this final model.

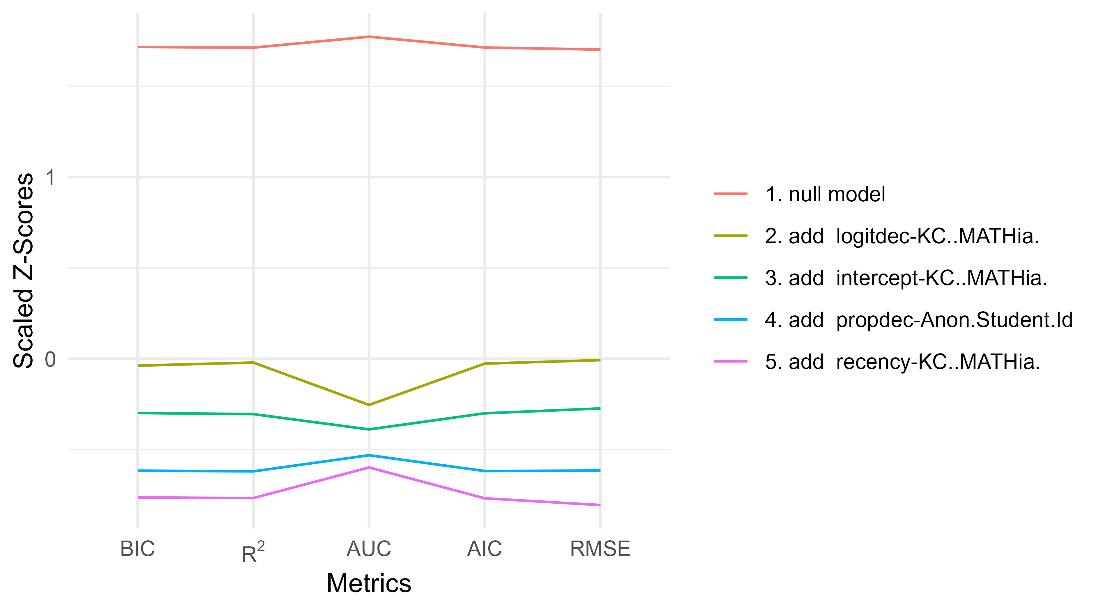
For the empty start, the final model is specified in feature(component) notation; see the equation below.

$$propdec(Anon.Student.Id) + intercept(KC..MATHia.) + recency(KC..MATHia.) + logitdec(KC..MATHia.)$$

See Table 6 and Figure 6 for the step actions that led to this final model.

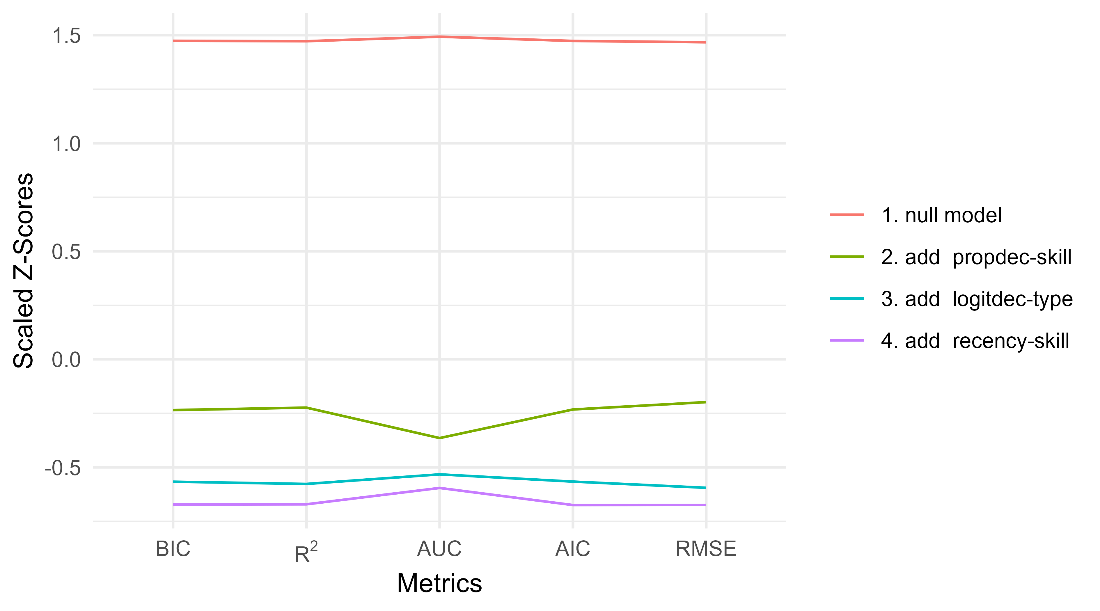
ASSISTments 2012-2013 Dataset

For the empty start, the final model is specified in feature(component) notation; see the equation below.

$$propdec(skill) + logitdec(type) + recency(skill)$$

See Table 7 and Figure 7 for the steps leading to this final model.

After this search process, we accepted the base model with propdec for skill, logitdec for type, and recency for skill. We did a simple crossvalidation of this model with the problem difficulty intercept added for the 10 difficulty levels. For this model, we added the problem_difficulty level, which we inferred from the held-out folds when we crossvalidated the model. Inspired by the approach to problem difficulty estimation adopted by IKT (Minn et al., 2022), we chose to represent problem difficulty with 10 levels. This compression also greatly simplified the model search process with both stepwise and LASSO regression. The problem difficulty was computed by finding the mean correctness for each problem_id in the held-out data and then using k-means to determine nine cut points for the means. This method defined 10 ranges, e.g. 0 to .00022, .00022 to .21, .21 to .34, etc., labeled a through j. We assigned each problem_id to a difficulty level according to this scheme, with problem_ids observed only four times being excluded and always labeled e. We assumed that any problem_ids that were unseen (i.e., in the held-out fold but not in the training fold) were labeled e. This method is remarkably similar to the method IKT used. So, we used the model from the 5^th fold of the crossvalidated stepwise search with the 5% and used that model to fit the 95% held out remainder of the data. For this model, we added the problem difficulty level, which we inferred from the held-out folds when we crossvalidated the model.

$$propdec(skill) + logitdec(type) + recency\left( skill) + intercept(difficulty\_ level \right)$$

Interestingly, the model was much improved by these difficulty levels, reaching near the levels of other methods described subsequently. The 5-fold CV in this 95 produced an AUC of 0.7590, SD = 0.0006.

LKT-LASSO

A primary goal of the LKT-LASSO analyses is to determine how well the approach can inform a researcher about which features are most important and guide the researcher toward a more interpretable, less complex, but reasonably accurate model. Figure 8 plots the relationship between the number of features and AUC across 100 values of lambda ranging from a large penalty that would reduce all feature coefficients to zero to a very small penalty that would retain all features. For all datasets, there are diminishing fit benefits as the number of features increases (from a smaller lambda). All curves have clear inflection points, which are used to provide example LKT-LASSO models. At the inflection points, the coefficients for most features drop to zero (see Table 8). Note in Table 8 that the MATHia dataset, in particular, fits quite well without many parameters for individual KCs. An LKT-LASSO model with lambda set to the value that would retain approximately 100 features outperformed DKT, SAKT, and IKT on all datasets. In two of the three datasets, the LKT-LASSO models with approximately 25 features outperformed those models. The features retained in these models appear to be the more robust and important features.

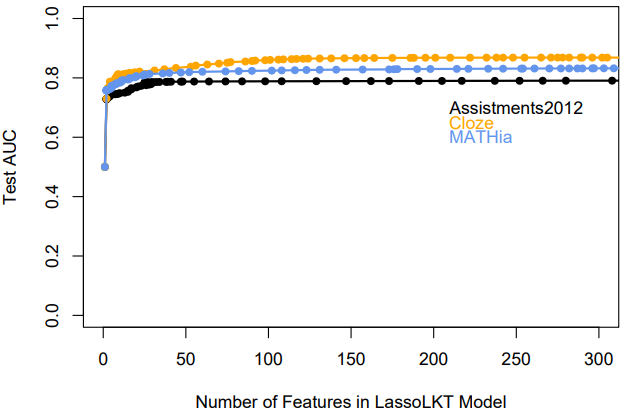
The final features that remained for LKT-LASSO models near the inflection points partially overlapped with those found with our stepwise regression approach, as expected. Below, the top 10 features for each dataset are listed in order of relative importance (see Tables 9, 10, and 11 below). When the results did not agree with the stepwise results, it appears that it may be because a stricter lambda should be employed. For instance, a recency feature for the Problem.Name KC with decay parameter .1 remained in the MATHia dataset. However, it has a negative coefficient, which is challenging to interpret given that the negative sign implies that correctness probability increases as time elapses. A larger lambda value may be justified.

For the cloze dataset, a large number of features remained even at the inflection point (~150), and they were missing many features we stepwise added. Inspecting the features, we saw that the variance stepwise captured in single terms (e.g., recency with decay parameter = .5 vs. multiple recency features with different decay parameters) was distributed across many terms in LKT-LASSO. Given that one goal of this work is to make simpler and more easily interpretable models for humans, we tried a larger penalty to reduce the number of features to ~25. The resulting top 10 if these are in Table 9. This model is more interpretable to a human, with mostly recency features, recency-weighted proportion features, and counts of success for KC. While the match to stepwise is not exact, we can now see it attending to student and KC successes and failures with features like logitdec in the top 10. It appears that lambda values are a sort of human interpretability index. Larger values make the resultant models more human-interpretable and, in this case, still create well-fitting models. Overall, the agreement between the approaches is encouraging evidence that these methods behave consistently.

Comparative Results

Tables 12, 13, and 14 below show the comparative results of the models we tested. The table for each dataset is sorted by AUC to show the highest AUC on top.

Methods Discussion

Stepwise Model Fitting

Cloze with Stepwise

For the cloze dataset, the models from the three starting points produce somewhat different results, illustrating the problem with any stepwise method due to it not being a global optimization. However, considering our goal is to implement these models, the result also suggests a solution to this local minimum problem. By using more than one starting point, we can identify the essential features that explain the data.

For example, these cloze results show that the recency feature used for the KC-Default is particularly predictive. In this dataset, it simply means that the time since the last verbatim repetition (KC Default) was a strong predictor, with more recent time since the last repetition leading to higher performance. Successes were also important, but curiously, they matter most for the KC-Correct-Answer. In all cases, the log of the success is the function best describing the effect of the correct responses. In this dataset, this means that each time they responded with a fill-in word, and it was correct, they would be predicted to do better the next time that word was the response. The log function is just a way to bias the effect of successes to be stronger for early success. While the recency being assigned to the exact repetitions (KC-Default) indicates the importance of memory to performance, the tracking of success (as permanent effects) across like responses suggests that people are learning the vocabulary despite showing forgetting.

Consistent across all three final models is also the attention to student variability modeling. In BestLR, the log success and failure predictors for the student in the model mean that the student intercept is removed in an elimination step as redundant (this is also due to the BIC method, which penalizes the student intercept as unjustifiably complex). Interestingly, in the AFM and empty start models, we find that the propdec feature is added to capture the student variability after the intercept is removed since these starting models did not trace student performance with their start log success and failure feature, as did BestLR from the start. The MATHia data has the same “problem” with BestLR start because BestLR serves as enough of a local minimum to block the addition of terms. Practically, these features are important since they allow the model to get an overall estimate for the student that greatly improves the prediction of individual trials.

In summary, there appears to be no great advantage to starting with a complex starting model. Indeed, in all cases, the BIC stepwise procedure greatly simplifies the models by reducing the number of coefficients. It appears that prior models produced by humans (in this case, AFM and BestLR) do not produce better results in the model space than simply starting with an empty null hypothesis for the model. Furthermore, all three start models result in final models with no fixed student parameters, so they should work for new similar populations without modifications, unlike AFM and BestLR, which relied on fixed student intercepts.

MATHia with Stepwise

Practically speaking, for the MATHia case, we also see the importance of student variability, recency, and correctness for KC and item for all the models. We can see that the BestLR start has some effect on the quantitative fit and chosen model. Most notably, while AFM and empty starts result in the student intercept being dropped in favor of logitdec and propdec, respectively, the BestLR start retains the log successes and failures predictors for the student. At the same time, BestLR, perhaps because it begins with the Problem.Name intercept as a term, adds more features for Problem.Name, such as linesuc and recency. Additionally, all the models retained an intercept for the KCs, and all of the models captured MATHia KC performance change with the logitdec feature.

ASSISTments with Stepwise

The ASSISTments data require a more hybrid approach because the dataset had 50376 problem_ids, and the authors of this paper did not have convenient access to computers with enough memory/speed to accomplish the task. So, we created the 5% dataset (with 5 folds) to accomplish the stepwise search. Still, however, the AFM and BestLR searches were taking too long due to the large data size and the necessity of calculating such big models (which do not crossvalidate well since the data was student stratified and they tend to rely on student intercepts, which do not generalize when students are stratified across folds). However, we compressed the problem_ids and added them to the model found with the stepwise method for the 5% solution. We found that this caused a relatively large increase in AUC of .06, with the resulting model comparing well with the alternatives, as we saw in Section 4.3. This result illustrates an issue with using large datasets. It is not clear that when a dataset is very large, it allows a better model to be learned. In fact, if the model requires large datasets to find an effect, it typically implies the effect is not very strong or important to fit.

LASSO Model Fitting

LASSO regression (aka L1 regularization) applies an additional penalty term to the absolute values of the coefficients during fitting. Thus, larger coefficients will incur a larger penalty. Features that are highly correlated with other features may have their coefficients reduced to zero. It appears to be the case that relatively few variables can effectively track student learning, so there is no reduction in accuracy in search of simplicity. We used a particular implementation of LASSO, glmnet (Friedman et al., 2010; Tay et al., 2023). Rather than attempting to solve the model for a particular lambda value, the entire solution space is explored. This method means that many values of lambda (the default is 100) are used, from the minimum value necessary to reduce all coefficients to zero (the largest lambda penalty) to the minimum value that will retain all coefficients (the smallest lambda). For instance, for the ASSISTments 2012-2013 dataset, lambdas ranged from 0.172 to 0.00003, with the value that retained 100 features being 0.0018.

Fitting the LKT-LASSO models was relatively fast, with a few seconds for MATHia and cloze and several minutes for ASSISTments2012. Parallelization is possible since a significant aspect of the training is that we are fitting 100 models (1 per lambda). We implemented LKT-LASSO such that each individual item and KC were treated as separate features with coefficients that could be reduced to zero. This decision is not a requirement of LASSO since groups of features can be considered together. However, treating them separately has the interesting effect of simultaneously testing the importance of the student and KC model intercept features. This implicit comparison can reveal redundancies in either side of the model (student or KC model) that warrant further scrutiny. If specific features must remain, they can also be omitted from the regularization process.

The present results indicate that a linear combination of linear and nonlinear features can outperform popular alternatives. A linear combination of recent performance features (Galyardt and Goldin, 2015), temporal recency (Wixted and Ebbesen, 1997), counts of successes and failures (Pavlik et al., 2009), and KC/item difficulty parameters appear sufficient for knowledge tracing, at least for the contexts that generated the present data. Linear models have several practical advantages. For one, linear models allow easier explanation (and ablation) of what the model is using to track student performance (e.g., for ASSISTments we can say “problem difficulty, temporal recency, and recent performance are the most important features for predicting student success”, see Tables 9, 10, and 11). The ability to read off what is being accounted for also allows easier remediation of what is not being addressed. For instance, if the LKT-LASSO plot was not tracking the effect of time (Figure 10) and did not have a temporal feature, the solution would be obvious (add a temporal feature). Potential solutions are more complicated for DKT, such as updating the architecture to include an encoder layer to receive other inputs (Zhang et al., 2017). Although the sparkle of deep learning approaches may make non-technical stakeholders more likely to be interested in implementing them in products, managing more inscrutable deep learning models may be more complicated than logistic regression models. This issue is important because if the models are intended for practical applications, they may need to be maintained and updated regularly over years.

General Discussion

The results suggest that both stepwise and LASSO methods work excellently to create, improve, and simplify student models using logistic regression. Both approaches agreed that recency features, logsuc, and recency-weighted proportion measures like propdec and logitdec were important. They also agreed that the number of necessary features was substantially less than the full models. While some have argued against stepwise methods (Smith, 2018), we think that stepwise methods worked relatively well here because the feature choices were not arbitrary. We did not simply feed in all the features we could find. Instead, we choose a set of features that can be theoretically justified.

In general, we find that relatively simple logistic regression models work as well as the latest variants on deep knowledge tracing. Like Gervet et al. (2020), we find that logistic regression competes well with complex methods and outperforms them in many cases, producing an explainable model. Explaining the results from these logistic regression models needs to begin with consideration of the individual features. Each feature being found for a model means that the data fits better if we assume the feature is part of the story for learning in the domain. Clearly, we might expect different features for different learning domains, and practically, knowing the features predicting learning means that we can better understand the learning. For example, knowing that recency is a factor or knowing that overall student variability has a big effect. An expert building instruction technology might also use individual features or the overall predictions in an adaptive learning environment to make decisions about student pedagogy or instruction.

A key claim of IKT is that it is “interpretable” due to being able to separate student mastery, problem difficulty, and student ability (transfer ability) into separate input features. We replicated the efficacy of their approach of clustering items into 10 levels instead of using separate per-item parameters. Indeed, the best-fitting model for the ASSISTments2012 dataset (LKT-LASSO₁₀₀) used their approach of clustering items by difficulty instead of item intercepts. However, examining their explanation of their model, we might wonder whether interpretable is enough. Specifically, AI researchers often strive for a higher standard than interpretable, and AI research often strives for explainability. Interpretability helps one make sense of the model's output for decision-making, while explainability provides a more comprehensive understanding of how the model arrived at a result. Explainable AI serves a critical function in learning technologies by fostering trust and understanding between human users and machine algorithms, which is particularly important in educational settings where the outcomes can significantly affect learners' academic and professional futures. By elucidating the decision-making process, educators, students, and administrators can scrutinize, validate, and even challenge the recommendations or assessments provided by AI, thereby ensuring ethical and accurate application. Others have noticed that generalized additive models (GAMs) like ours have this character of being straightforward to explain (Khosravi et al., 2022).

Moreover, explainability in AI can pave the way for more informed and collaborative decision-making in educational planning, as it allows for nuanced discussions based on how and why certain conclusions were derived, thereby enhancing the effectiveness and equity of learning environments (Khosravi et al., 2022). Given this, we might argue that IKT, with its mixed methods from BKT, DKT, and machine learning, would be hard to explain to users, even if its outputs are interpretable. It is interpretable since it can be used to infer many pedagogically relevant values, but it seems that it would be difficult to explain the source of these values clearly. In contrast, each feature in LKT is relatively easy to explain, and logistic regression may be the simplest AI method possible because it is an additive combination of effects.

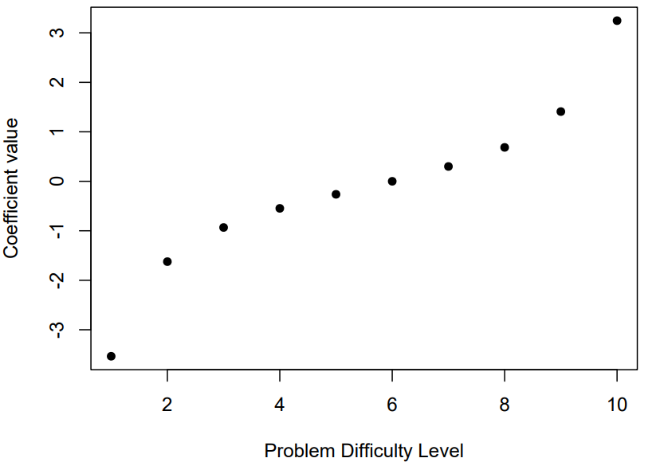
On some level, we might question the importance of the relationships between KCs based on these results. With the ASSISTments2012 dataset, the strong stepwise LKT results imply that relationships among items and KCs are much less a factor in the good fits of these methods than is accounting for problem difficulty. This suggestion seems likely because we get a very high AUC CV in the held-out data despite our model having few parameters and no explicit transfer among KCs. Consider this graph (Figure 9) of the intercepts for the 10 levels for problem difficulty in the LKT models, showing the large difference between the pools.

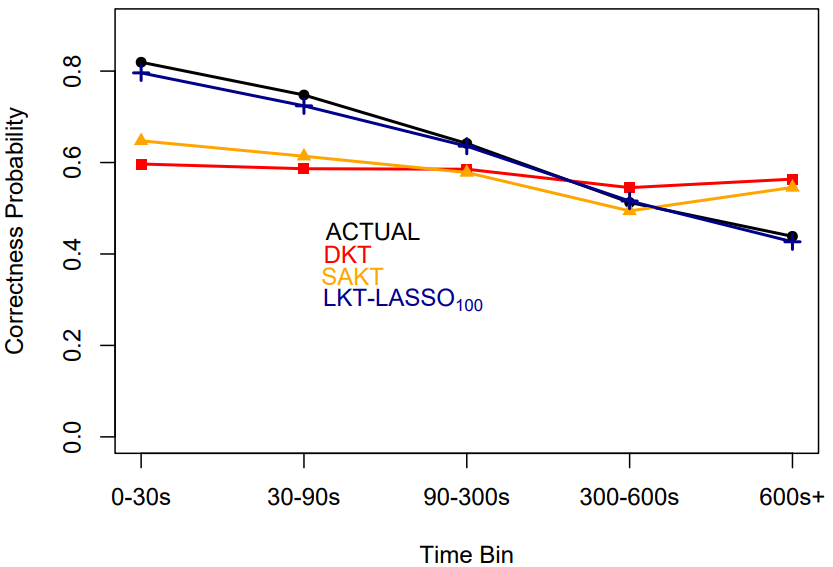
While DKT, SAKT, and IKT may be successful because they model relationships, LKT is likely successful because it captures the functional form of learning. LKT may be doing well despite the importance of relationships because it captures temporal factors more effectively; for example, see Figure 10. LKT also traces the mean performance across repetitions of a KC more effectively, see Figure 11.

We do not doubt that DKT or SAKT could be modified to address some of these issues. However, even if it did and matched LKT-LASSO's performance, why bother? Unless a major leap in performance is achieved, it might be worth considering that achieving AUC>.80 with 25 features is evidence that LKT works excellently, and we should focus our efforts on how to use such models, e.g., the decision rules these models should be paired with (Eglington and Pavlik Jr, 2020) or the methods to create interpretable student-facing dashboards based on the model.

Limitations and Future Work

A primary limitation of the present work is that we only included a subset of the LKT features already known and established theoretically. We also did not include some known features (e.g., spacing effects, long-term forgetting, and interactions among features). An extension of this work will be to include more features and a step to generate and test novel features that may be counterintuitive. For instance, KC model improvement algorithms could be incorporated into the process (Pavlik Jr et al., 2021). However, how much variance is left to explain that is not covered by the set of features we used? With two datasets, models with AUC > .8 were found using only a relatively small subset of the potential features. On the third dataset (ASSISTments2012), the highest AUC among the models was found with LKT-LASSO₁₀₀.

An opportunity for future work may also be to use these LKT features as components in other model architectures, such as Elo or deep learning approaches. Elo modeling is also particularly promising due to its simplicity and self-updating function (Pelánek, 2016). Elo can be adjusted to include KT features like counts of successes and failures (Papousek et al., 2014). However, standard Elo without KT features is also a strong null model since it does reasonably well without KT features.

Future work might also explore how LKT-LASSO offers a convenient opportunity to evaluate the learner and KC model simultaneously. Within the LASSO approach, the coefficient of each KC can be pushed to zero, and this could be used to allow refinement of the KC model. A limitation of our work here is that we did not explore this further, merely observing that only some KCs were being assigned intercepts in the models.

A key limitation of the stepwise method is the individuality of features resulting in local optima. This limitation is illustrated by how logsuc and logfail are retained in the BestLR MATHia model, but they are not added in any of the other models. Their retention in BestLR may be best, but it may also reflect the standard tendency of stepwise methods to block the addition of new terms (possibly better) that are collinear with prior terms. This problem may be unavoidable, but we think it is also an uncommon problem. The other side of the problem is that logsuc and logfail are not added for the student when nothing is already present. This local decision is because adding both requires two steps of the algorithm, while adding composite features like propdec or logitdec requires one step. Since stepwise selection is based on a greedy step optimization, it ignores better gains that might occur in two steps when it can accomplish the solution pretty well in one step.

A solution to this problem of feature grain size, in which complex features are favored because they contain multiple sources of variability, might be to create synthetic linear feature groupings that can be chosen as an ensemble for addition to the model with each step. Such a fix will allow us to add the combination feature logsuc and logfail (e.g., for the students) using two coefficients as usual, but in one stepwise step. This solution will allow the combined feature to compete with other terms, such as logitdec or propdec, which incorporate success and failure combined. More advanced methods can use factor selection, which might be applied in both stepwise and LASSO within LKT, such as grouping specific features together, such as KC models (Yuan and Lin, 2006).

Presets

To make the process of logistic regression modeling efficient yet still retain some flexibility and user control, our tool includes several preset feature palettes that users will have available instead of specifying their own list. These presets are essentially a collection of theoretical hypotheses about the nature of the student model, given some goal of the modeler. The presets include the following four presets.

• Static - This present will contain only the intercept feature. It allows for neither dynamic nor adaptive solutions, essentially finding the best IRT-type model unless the item or KC component is not used, in which case it finds a single intercept for each student. Essentially, it fits the LLTM model (Fischer, 1973).
• AFM variants (i.e., dynamic but not adaptive) – This preset fits linear and log versions of the additive factors model (Cen et al., 2008), including LLTM terms that represent different learning rates or difficulties based on KC groupings (using the $ operator in LKT syntax).
• PFA and BestLR variants (dynamic and adaptive but recency insensitive) – This preset contains all of the above mechanisms and also includes the success and failure linear and log growth terms used in PFA (Pavlik Jr. et al., 2009) and BestLR (Gervet et al., 2020).
• Simple adaptive – This catchall preset will include rPFA (Galyardt and Goldin, 2015) inspired terms such as logitdec and propdec, described in this paper and elsewhere (Pavlik et al., 2021). In addition, it will include temporal recency functions using only a single nonlinear parameter, the best example of which, recency, was described in this paper and has been previously described (Pavlik et al., 2021).

Integrating Deep-learning with research-based features

One takeaway from this work is that deep learning approaches like DKT struggle to discover fundamental features of learning and forgetting that are captured easily by counts of successes and failures (e.g., Pavlik Jr. et al., 2009; Roediger and Butler, 2011), elapsed time (recency) (e.g., Judd and Glaser, 1969; MacLeod and Nelson, 1984), and recent performance changes (e.g., Galyardt and Goldin, 2015; Pavlik et al., 2021). The inability of DKT to predict performance as a function of counts of prior successes (Figure 11) or elapsed time (Figure 10) indicates a significant limitation. It is worth noting that although SAKT also struggled to predict performance as a function of elapsed time, it did predict performance as a function of prior successes fairly well. The successes and failures of the different models became apparent when we plotted their predictions for fundamental learning scenarios (accumulated practice and elapsed time). We recommend this approach whenever models are developed in the future. Future work should attempt to integrate the benefit of highly explainable features that lead to superior performance with high flexibility and reduced assumptions of deep learning approaches. Discovering high-level interactions among explainable features may allow deep learning approaches to provide an advantage over simpler, more explainable models.

Conclusion

As described in our introduction, an initial motivation of this work was to reconcile the tension between model accuracy and explainability. Surprisingly, we found that relatively simple regression models could be more accurate and more explainable in all tested datasets. We find that the first few selected features in most models produced by the stepwise procedure are both effective AND explainable. Articulating a theory to describe the simple models is relatively easy since some research-based argument can justify each feature. For example, we see the importance of tracing student-level individual differences in all the models, and we see the recency feature as indicating that forgetting occurs. The LASSO procedure largely confirms that the stepwise models are not far from a more globally optimal solution for our test cases and reveal the future of the endeavor because of the higher likelihood of a more global solution with LASSO despite the slightly less interpretable models.

The present work sought to simplify the learner model-building process by creating a model-building tool released as part of the LKT R package. Our promising results demonstrate two modes our tool has available to build models automatically. With the stepwise method, they can start with an empty model, provide sample data, and the fitting process will provide a reasonable model with a reduced set of features according to a preset criterion for fit statistic change. Alternatively, with the LKT-LASSO approach, the user provides data, and the resulting output will be a set of possible models of varying complexity based on a range of lambda penalties.

Acknowledgments

This work was partially supported by the National Science Foundation Learner Data Institute (NSF #1934745) project and a grant from the Institute of Education Sciences (ED #R305A190448).

Editorial Statement

Philip I. Pavlik Jr. was not involved with the journal’s handling of this article to avoid a conflict with his role as Editorial Team Member. The entire review process was managed by Special Guest Editors Mingyu Feng and Tanja Käser.

References

1. Cen, H., Koedinger, K. and Junker, B. 2006. Learning Factors Analysis: A General Method for Cognitive Model Evaluation and Improvement. In Proceedings of the International Conference on Intelligent Tutoring Systems, Jhongli, Taiwan, M. Ikeda, K. D. Ashley and T.-W. Chan Eds. Springer, 164-176.
2. Cen, H., Koedinger, K. R. and Junker, B. 2008. Comparing two IRT models for conjunctive skills. In Proceedings of the Proceedings of the 9th International Conference on Intelligent Tutoring Systems, Montreal, Canada, B. Woolf, E. Aimer and R. Nkambou Eds. ACM, Inc., 796-798.
3. Chi, M., Koedinger, K. R., Gordon, G., Jordan, P. and VanLehn, K. 2011. Instructional factors analysis: A cognitive model for multiple instructional interventions. In Proceedings of the 4th International Conference on Educational Data Mining (EDM 2011), M. Pechenizkiy, T. Calders, C. Conati, S. Ventura, C. Romero and J. Stamper Eds. International Educational Data Mining Society, Eindhoven, The Netherlands, 61-70.
4. Conati, C., Porayska-Pomsta, K. and Mavrikis, M. 2018. AI in Education needs interpretable machine learning: Lessons from Open Learner Modelling. arXiv preprint arXiv:1807.00154.
5. Eglington, L. G. and Pavlik Jr, P. I. 2020. Optimizing practice scheduling requires quantitative tracking of individual item performance. npj Science of Learning 5, 15.
6. Feng, M., Heffernan, N. and Koedinger, K. 2009. Addressing the assessment challenge with an online system that tutors as it assesses. User Modeling and User-Adapted Interaction 19, 243-266.
7. Fischer, G. H. 1973. The linear logistic test model as an instrument in educational research. Acta Psychologica 37, 359-374.
8. Friedman, J., Hastie, T. and Tibshirani, R. 2010. Regularization Paths for Generalized Linear Models via Coordinate Descent. J Stat Softw 33, 1-22.
9. Friedman, J. H., Hastie, T. and Tibshirani, R. 2010. Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software 33, 1 - 22.
10. Galyardt, A. and Goldin, I. 2015. Move your lamp post: Recent data reflects learner knowledge better than older data. Journal of Educational Data Mining 7, 83-108.
11. Gervet, T., Koedinger, K., Schneider, J. and Mitchell, T. 2020. When is Deep Learning the Best Approach to Knowledge Tracing? Journal of Educational Data Mining 12, 31-54.
12. Gong, Y., Beck, J. E. and Heffernan, N. T. 2011. How to construct more accurate student models: Comparing and optimizing knowledge tracing and performance factor analysis. International Journal of Artificial Intelligence in Education 21, 27-46.
13. Hochreiter, S. and Schmidhuber, J. 1997. Long Short-Term Memory. Neural Computation 9, 1735-1780.
14. Judd, W. A. and Glaser, R. 1969. Response Latency as a Function of Training Method, Information Level, Acquisition, and Overlearning. Journal of Educational Psychology 60, 1-30.
15. Khosravi, H., Shum, S. B., Chen, G., Conati, C., Tsai, Y.-S., Kay, J., Knight, S., Martinez-Maldonado, R., Sadiq, S. and Gašević, D. 2022. Explainable Artificial Intelligence in education. Computers and Education: Artificial Intelligence 3, 100074.
16. MacLeod, C. M. and Nelson, T. O. 1984. Response latency and response accuracy as measures of memory. Acta Psychologica 57, 215-235.
17. Minn, S., Vie, J.-J., Takeuchi, K., Kashima, H. and Zhu, F. 2022. Interpretable Knowledge Tracing: Simple and Efficient Student Modeling with Causal Relations. In Proceedings of the AAAI Conference on Artificial Intelligence AAAI Press, 12810-12818.
18. Pandey, S. and Karypis, G. 2019. A Self-Attentive model for Knowledge Tracing. In Proceedings of the 12th International Conference on Educational Data Mining, C. Lynch, A. Merceron, M. Desmarais and R. Nkambou Eds. International Educational Data Mining Society, 384-389.
19. Papousek, J., Pelánek, R. and Stanislav, V. 2014. Adaptive practice of facts in domains with varied prior knowledge. In Proceedings of the Proceedings of the 7th International Conference on Educational Data Mining (EDM 2014), J. Stamper, Z. Pardos, M. Mavrikis and B. M. Mclaren Eds. International Educational Data Mining Society, 6-13.
20. Pavlik Jr, P. I., Eglington, L. and Zhang, L. 2021. Automatic Domain Model Creation and Improvement. In Proceedings of The 14th International Conference on Educational Data Mining, C. Lynch, A. Merceron, M. Desmarais and R. Nkambou Eds. International Educational Data Mining Society, 672-676.
21. Pavlik Jr, P. I. and Eglington, L. G. 2021. LKT: Logistic Knowledge Tracing. In CRAN R package version 1.0.
22. Pavlik Jr., P. I., Brawner, K. W., Olney, A. and Mitrovic, A. 2013. A Review of Learner Models Used in Intelligent Tutoring Systems. In Design Recommendations for Adaptive Intelligent Tutoring Systems: Learner Modeling, R. A. Sottilare, A. Graesser, X. Hu and H. K. Holden Eds. Army Research Labs/ University of Memphis, 39-68.
23. Pavlik Jr., P. I., Cen, H. and Koedinger, K. R. 2009. Performance factors analysis -- A new alternative to knowledge tracing. In Proceedings of the 14th International Conference on Artificial Intelligence in Education, V. Dimitrova, R. Mizoguchi, B. D. Boulay and A. Graesser Eds. IOS Press, Brighton, England, 531–538.
24. Pavlik, P. I., Eglington, L. G. and Harrell-Williams, L. M. 2021. Logistic Knowledge Tracing: A Constrained Framework for Learner Modeling. IEEE Transactions on Learning Technologies 14, 624-639.
25. Pelánek, R. 2016. Applications of the Elo rating system in adaptive educational systems. Computers & Education 98, 169-179.
26. Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L. J. and Sohl-Dickstein, J. 2015. Deep Knowledge Tracing. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), C. Cortes, N. Lawrence, D. Lee, M. Sugiyama and R. Garnett Eds. MIT Press, 1-9.
27. Roediger, H. L. and Butler, A. C. 2011. The critical role of retrieval practice in long-term retention. Trends in Cognitive Sciences 15, 20-27.
28. Schmucker, R., Wang, J., Hu, S. and Mitchell, T. 2022. Assessing the Performance of Online Students - New Data, New Approaches, Improved Accuracy. Journal of Educational Data Mining 14, 1-45.
29. Smith, G. 2018. Step away from stepwise. Journal of Big Data 5, 32.
30. Tay, J. K., Narasimhan, B. and Hastie, T. 2023. Elastic Net Regularization Paths for All Generalized Linear Models. Journal of Statistical Software 106, 1 - 31.
31. Vie, J.-J. and Kashima, H. 2019. Knowledge Tracing Machines: Factorization Machines for Knowledge Tracing. In Proceedings of the AAAI Conference on Artificial Intelligence, B. Williams, Y. Chen and J. Neville Eds. AAAI Press, 750-757.
32. Wixted, J. T. and Ebbesen, E. B. 1997. Genuine power curves in forgetting: A quantitative analysis of individual subject forgetting functions. Memory & Cognition 25, 731-739.
33. Xiong, X., Zhao, S., Van Inwegen, E. G. and Beck, J. E. 2016. Going Deeper with Deep Knowledge Tracing. In Proceedings of the 9th International Conference on Educational Data Mining, T. Barnes, M. Chi and M. Feng Eds. International Educational Data Mining Society, Raleigh, NC, 545-550.
34. Yuan, M. and Lin, Y. 2006. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68, 49-67.
35. Yudelson, M., Pavlik Jr., P. I. and Koedinger, K. R. 2011. User Modeling – A Notoriously Black Art. In User Modeling, Adaption and Personalization, J. Konstan, R. Conejo, J. Marzo and N. Oliver Eds. Springer Berlin / Heidelberg, 317-328.
36. Zhang, L., Xiong, X., Zhao, S., Botelho, A. and Heffernan, N. T. 2017. Incorporating Rich Features into Deep Knowledge Tracing. In Proceedings of the Proceedings of the Fourth (2017) ACM Conference on Learning @ Scale, Cambridge, Massachusetts, USA Association for Computing Machinery, 169–172.