Abstract

We propose a novel approach to address the issue of college student attrition by developing a hybrid model that combines a structural neural network with a piecewise exponential model. This hybrid model not only shows the potential to robustly identify students who are at high risk of dropout, but also provides insights into which factors are most influential in dropout prediction. To evaluate its effectiveness, we compared the predictive performance of our hybrid model with two other survival analysis models: the piecewise exponential model and a hybrid model combining a fully-connected neural network with a piecewise exponential model. Additionally, we compared it to five other cross-sectional models: Ridge Logistic Regression, Lasso Logistic Regression, CART decision tree, Random Forest, and XGBoost decision tree. Our findings demonstrate that the hybrid model outperforms or performs comparably to the other models when predicting dropout among students at the University of Delaware in Spring 2020, Spring 2021, and Spring 2022. Moreover, by categorizing predictors into three distinct groups—academic, economic, and social-demographic—we discovered that academic predictors play a prominent role in distinguishing between dropout and retained students, while other predictors may indirectly influence predictions by impacting academic variables. Consequently, we recommend implementing an intervention program aimed at identifying at-risk students based on their academic performance and activities, with additional consideration for economic and social-demographic factors in customized intervention plans.

Keywords

Introduction

College dropout continues to be a significant concern for higher education institutions (Albreiki et al., 2021; Aulck et al., 2016; Cannistra et al., 2022). Data from the National Center for Education Statistics (NCES) reveals that approximately 40% of first-time, full-time degree-seeking undergraduate students at 4-year degree-granting institutions fail to obtain a bachelor’s degree within six years at the same institution. Alarmingly, around 20% of these students drop out within their first year (NCES, 2022). The consequences of dropout are substantial, leading to wasted resources for students, institutions, and society as a whole. Students who discontinue their college education not only waste their time but also the tuition and fees they have paid and the loans they have borrowed, and tended to have lower income and an increased risk of living in poverty (Bouchrika et al., 2023). Concurrently, institutions suffer losses in terms of resources dedicated to these students, as well as potential tuition revenue and future alumni donations. On average, institutions lose approximately $10 million in tuition revenue annually due to attrition (Raisman, 2013). Furthermore, both federal and state governments waste their appropriations to institutions and grants to students, with an estimated expenditure of $9 billion between 2003 and 2008 on students who withdrew within their first year (Schneider, 2010).

Two main approaches have been developed to address the issue of college dropout: theory-driven and data-driven approaches (Cannistra et al., 2022). The theory-driven approach focuses on constructing conceptual models to comprehend the underlying reasons for dropout. It considers students’ decisions to discontinue their education as an interplay of various factors, including family background, demographic characteristics, academic performance, social integration, organizational determinants, personal satisfaction, and institutional commitment (Bean, 1980; Spady, 1970; Tinto, 1975). By developing these conceptual models and analyzing observed data, specialized recommendations can be derived to mitigate attrition (Bean, 1980). In contrast, the data-driven approach emphasizes dropout prediction. Statistical and machine learning models are utilized to forecast students’ academic performance and/or identify those who are at risk of dropping out (Aulck et al., 2016; Baker & Yacef, 2009; Heredia-Jimenez et al., 2020). However, this approach often involves a trade-off between interpretability and predictability. Recent studies have proposed various methods to improve the interpretability of predictive models (Agarwal et al., 2021; Baranyi et al., 2020; Cohausz et al., 2022; Kopper et al., 2021).

Our study aims to integrate the strengths of both approaches, as educational institutions require both explanatory insights and predictive capabilities to develop effective intervention plans for reducing attrition (Wagner et al., 2023). We predict the dropout risks of students who are currently enrolled at the start of an academic semester, more specifically, whether they will fail to enroll for the subsequent semester. This allows the student advising team sufficient time to develop and implement effective intervention strategies throughout the semester and assists the Budget Office to estimate the tuition revenue from the current students. To model college students’ dropout risks, we employ a piecewise exponential model (Kopper et al., 2021; Friedman, 1982). This model is well-suited for analyzing longitudinal processes in students’ academic careers, which involve time-varying factors and effects associated with dropout risks. While this classic survival analysis model offers interpretability, it may not provide optimal predictive performance. To enhance predictability, we introduce a neural network model into the piecewise survival analysis to capture the hazard, which transitions from a linear combination of variables in traditional survival analysis to a nonlinear function of the variables. However, fully-connected neural network models pose challenges to interpretability due to their black-box nature. To address this dilemma, we employ a structural neural network (Fan et al., 2022; Köhler and Langer, 2021; Schmidt-Hieber, 2020), where we impose a structure inspired by theoretical frameworks of student attrition onto the neural networks. Specifically, we categorize variables into three groups: academic, economic, and socio-demographic. Variables within each category interact with each other, forming hidden layers that generate a final neuron representing the category. In total, three final neurons are generated. These final neurons are then linearly combined to predict the hazard, which is subsequently converted into dropout probabilities. Consequently, our model not only provides a list of students with a high risk of dropout but also identifies whether students are more likely to dropout due to academic performance (Stinebrickner & Stinebrickner, 2014), financial burden (Cai & Fleischhacker, 2022), or social integration (Stage, 1989).

The primary objective of this study is to address two key research questions that will contribute to the design of an effective intervention plan for attrition reduction:

1. Does the utilization of a structural neural network enhance predictive performance compared to traditional survival analysis models that employ linear hazards?

2. Which category or categories of variables impact(s) the prediction of students’ dropout risks?

Literature Review and Conceptual Framework

Extensive academic research has been conducted on college student dropout, employing both theory-driven and data-driven approaches. The theory-driven approach aims to establish a theoretical foundation and develop conceptual models to comprehend students’ dropout decisions. Tinto (1975) formulated a theoretical model based on Durkheim’s suicide theory (Durkheim, 2005) and a cost-benefit analysis, which sought to explain dropout decisions through the interaction between individuals and institutions. The model suggested that factors such as family background, individual characteristics, and pre-college schooling influence individuals’ integration within the academic and social systems of colleges, subsequently impacting their commitment to educational goals and institutional commitment. Lower levels of commitment were found to be associated with higher dropout probabilities. Bean (1980) developed a causal model inspired by turnover models in work organizations, positing that the interaction between students’ background characteristics and organizational factors affects their satisfaction, institutional commitment, and ultimately dropout probabilities. The model was empirically tested using multiple regression and path analysis, utilizing questionnaires returned by 1,195 new freshmen. Gender-specific recommendations were provided to reduce attrition. Similarly, Spady (1970) developed a sociological model of the college dropout process, drawing from Durkheim’s suicide theory (Durkheim, 2005). Spady argued that family background influences students’ academic potential and normative congruence, subsequently impacting their grade performance, intellectual development, and friendship support. The interaction of these factors influences social integration, ultimately leading to dropout decisions. These conceptual models have provided theoretical guidance for subsequent empirical studies (Aina et al. 2022; Deike 2003; Márquez-Vera et al. 2016).

Our conceptual framework draws inspiration from Tinto's theoretical model (Tinto, 1975) and aims to capture the longitudinal process of dropout risk accumulation. We posit that students' dropout risks are determined by their goal commitment and institutional commitment, which are influenced by the interplay of academic integration, economic integration, and social integration. Academic integration is shaped by factors such as college cumulative GPA, the number of classes with a grade below D, the number of credits registered, and engagement in multiple majors. Pre-college schooling indicators, such as high school GPA and the number of Advanced Placement (AP) credits, also contribute to academic integration. Economic integration is influenced by variables including expected family contribution (EFC), outstanding balance, and the amount of financial aid received in the form of grants, scholarships, and loans. Social integration encompasses factors such as eligibility for Pell Grants (whether total family income is less than or equal to $50,000 U.S.) and being a first-generation college student, as well as demographic characteristics including gender and racial ethnicity. Importantly, the dropout risk of a student evolves each semester, reflecting the changing dynamics of the three integrations. These changes stem from time-varying factors like academic performance and financial aid, the evolving processes that generate the integrations, and the dynamic interactions among them.

The data-driven approach, as an alternative, emphasizes prediction, specifically the identification of students at high risk of dropout as candidates for targeted intervention and remedial programs (Quadri and Kalyankar, 2010). Various statistical and machine learning methods have been employed in this approach. Almarabeh (2017) compared five classification methods, including Naïve Bayes, Bayesian network, decision tree with ID3, decision tree with C4.5, and multilayer perceptron neural network, to predict the dropout risks of 225 students using 10 predictors. The Bayesian network model exhibited the best performance across various error measures, such as accuracy, true positive rate, false positive rate, and F-score. Similarly, Sandoval-Palis et al. (2020) compared logistic regression and neural network models to predict the dropout risks of 2,097 students in an engineering university in Ecuador, using four predictors, regime, leveling course type, application grade, and vulnerability index, where regime, leveling course type, and application grade were academic factors, and vulnerability index was derived from 25 socio-economic variables. The neural network models outperformed logistic regression models in terms of accuracy and AUC score. However, despite their high predictive power, neural network models are challenging to interpret due to their black-box nature.

Regression and decision tree models are preferred when the predictive performance is satisfactory, as their interpretability can aid institutions in establishing effective intervention policies. Wagner et al. (2023) compared three explainable methods and two ensemble methods to predict degree dropout in a middle-sized German university. The explainable methods are decision trees, K-nearest neighbors, and logistic regression, and the ensemble methods are AdaBoost and Random Forest. Among these, logistic regression was found to exhibit the best overall predictive performance. Nevertheless, the study also highlighted that these models did not equally excel in predicting student subpopulations, particularly concerning gender and specific study programs. Quadri and Kalyankar (2010) proposed a hybrid method for dropout prediction in an Indian institution, combining decision trees to identify relevant predictors, such as parents’ income and previous semester’s grades, with logistic regression for predicting students’ dropout risks. Aulck et al. (2016) utilized regularized logistic regression, Random Forest, and K-nearest neighbors to predict the attrition of 32,538 students from the University of Washington, finding that regularized logistic regression performed the best. Strong predictors included GPA in math, English, chemistry, and psychology classes. Heredia-Jimenez et al. (2020) employed Random Forest to predict at-risk students across 65 undergraduate programs in a public engineering-oriented university in Ecuador. They obtained reliable predictions by excluding socio-demographics and pre-college entry information, relying solely on academic information as predictors. Ameri et al. (2016) compared the performance of multiple methods, such as logistic regression, adaptive boosting, decision tree, Cox regression, and time-dependent Cox regression, in predicting dropout at Wayne State University. Time-dependent Cox regression was identified as the best method due to its ability to incorporate time-varying predictors, demonstrate superior predictive performance, and predict the timing of dropout events.

Recent research efforts have focused on enhancing the interpretability of data-driven models in predicting college student attrition. For instance, Baranyi et al. (2020) utilized deep neural networks and gradient boosted trees for dropout prediction while attempting to interpret the models using techniques like permutation importance and SHAP importance. Márquez-Vera et al. (2016) introduced an Interpretable Classification Rule Mining (ICRM) algorithm based on IF-THEN rules to predict high school dropout early on. They compared this approach with classical classification methods and data resampling techniques, suggesting its use in an early warning system. Cohausz (2022) proposed a three-step framework that includes identifying important features, understanding counterfactuals, and uncovering causal relations. This framework combines machine learning interpretability techniques with social science-based causal reasoning. Agarwal et al. (2021) introduced Neural Additive Models (NAMs), which combine deep neural networks with generalized additive models to improve accuracy while maintaining interpretability. Their experiments demonstrated that NAMs outperformed traditional models and were competitive with state-of-the-art interpretable models like Explainable Boosting Machines (EBMs) and Gradient Boosted Trees. Kopper et al. (2021, 2022) presented an approach that combines deep neural networks with piecewise exponential models, resulting in inherently interpretable models capable of processing unstructured data sources.

Data and Variables

In accordance with our conceptual framework, we collected data encompassing academic, economic, and socio-demographic aspects from the enterprise data warehouse of the University of Delaware (UD). UD, a public research university, has an undergraduate population of approximately 18,000 students. The dataset under examination comprises information from 40,440 undergraduate students who commenced their journey as first-time full-time students during the fall semesters between 2012 and 2021. Appendix A provides a detailed breakdown of student headcounts by cohort and by semester. The raw data tables have been thoughtfully curated into a final dataset for analysis, structured as a student-semester file, with each row representing a student in a particular semester. The final dataset is stored in an encrypted shared drive of the Office of Institutional Research and Effectiveness at UD. Student IDs that serve as unique identifiers are not used in the analysis. No linking list has ever been created or maintained that might connect study data to specific individuals.

Students were tracked until the end of their third year or until dropout occurred. Only fall and spring semesters were considered for tracking purposes, and dropout was defined as not being graduated after the current semester and not re-enrolling in the next semester. Table 1 provides a description of the dependent and independent variables, along with their means (and standard deviations for numeric variables) for each semester. The dependent variable indicates whether a student is enrolled in the next semester, with a value of 1 representing dropout and 0 representing enrollment. It is imperative to note that our dataset is imbalanced, particularly concerning the dependent variable. The average dropout rate increased from the first semester (0.033) to the second semester (0.047) and then gradually decreased in the subsequent four semesters: 0.025, 0.023, 0.013, and 0.01 from the third to the sixth semester, respectively. The pronouncedly low dropout rates pose a significant challenge in identifying students at a high risk of dropout.

Our dataset comprises thirteen academic variables, consisting of four binary variables and nine numeric variables. In the first fall semester, all students were full-time students, and the majority remained full-time throughout their academic journey. During the first semester, 16.9% of students were in the University Study program, which allowed them to explore and choose majors later. As students progressed to their sophomore and junior years, the percentage of students in the University Study program gradually decreased to 0.9% by the sixth semester. In the first semester, no students had a double major, but the percentage of students with a double major increased to 14.4% by the sixth semester.

Due to the data collection process on the census day of each semester (two weeks after the semester starts), students' academic standing status was not available in the first semester. There were 6.4% of students in probation status in the second semester, and the proportion gradually decreased to 1.3%. Similarly, these variables are not available in the first semester: College GPA, DFW (class grades being D, F or Withdraw) Count, Listener Count, Academic Standing, and Total Credit. In addition, the Total Credit, Total Minor Credit, Total Transfer Credit, and Total Advanced Placement (AP) Credit variables were standardized by the typical 120 credits required for graduation, and the Registered Credit variable was standardized based on the typical total of 15 credits taken in one semester. For example, total credit rate being 0.25 means that a student has 30 (0.25x120) credits in total as of the census day of a semester, and registered credit rate being 0.8 means that a student registered 12 (0.8x15) credits in a semester.

From the second semester to the sixth semester, the average cumulative GPA increased from 3.103 to 3.229, the average DFW class count decreased from 0.371 to 0.249, the average Listener class count decreased from 0.062 to 0.034, and the average total credit rate increased from 0.18 to 0.716. From the first semester to the sixth semester, the average registered credit rate decreased from 1.02 to 0.991, the average total minor credit rate increased from 0.001 to 0.048, the average total transfer credit rate increased from 0.017 to 0.026, and the average total AP credit rate increased from 0.034 to 0.04. The average high school GPA varied slightly between 3.758 and 3.766 due to changes in the student population each semester.

All economic variables are numeric and standardized by the cost of attendance (COA). For instance, a grant/scholarship rate of 0.2 indicates that 20% of the COA is covered by grants and scholarships. Among the six semesters, the average Expected Family Contribution (EFC) rate varied between 0.819 and 1.005, the average grant/scholarship rate varied between 0.165 and 0.228, the average Parent Loan for Undergraduate Students (PLUS) parent loan rate varied between 0.036 and 0.053, the average student loan rate varied between 0.128 and 0.147, the average work-study aid rate varied between 0.003 and 0.006, and the balance varied between -0.012 and -0.016. The balance for the first semester is not available as of the census day.

All social variables, except for Age, are binary variables. From the first semester to the sixth semester, the average age increased from 18.023 to 20.442, the proportion of Pell Grant recipients decreased from 15.1% to 12.6%, the proportion of first-generation college students decreased from 12.8% to 11.8%, the proportion of male students varied between 40.0% and 40.5%, the proportion of Delawarean students increased from 31.7% to 32.7%, the proportion of African American students decreased from 5.2% to 4.6%, the proportion of Asian students varied between 5.1% and 5.3%, the proportion of Hispanic students decreased from 9% to 8.2%, and the proportion of White students increased from 72.8% to 74.4%.

Statistical Model

Our statistical model is designed to integrate the theory-driven and data-driven approaches, resulting in an "information-driven" framework (Cannistra et al., 2022). The proposed model, a piecewise exponential model with structural neural network (PEM-SNN), combines a structural neural network and a piecewise exponential model to predict dropout probabilities following a similar conceptual approach to Kopper et al.'s work (2021, 2022). However, our neural network is tailored to align with the conceptual framework inspired by Tinto's theoretical model (Tinto, 1975). This piecewise exponential model is designed to predict dropout probability using a hazard function generated by the structural neural network. The hazard function is a linear combination of three integrations, each of which represents a separate group of variables related to academic, economic, and social factors. For instance, the academic integration is derived solely from academic variables. We introduce the PEM-SNN in Section 4.3 after introducing the development of two more basic alternative models and follow it with sections on loss function construction and model training and evaluation.

Piecewise Exponential Model

We begin with a standard piecewise exponential model (PEM), a type of discrete event history analysis that provides interpretable coefficients. An event occurs if a student drops out from the institution they are currently enrolled in by the end of the third year. Otherwise, the student is considered to be “censored” or “survived”. For a student $i$ in a semester $j$, Equation (1) defines the logarithm of the hazard function $\log\left( h_{i}\lbrack j\rbrack \right)$ to be the sum of baseline hazard $h_{0}\lbrack j\rbrack$ and a linear combination of the student attributes $X_{0i}\lbrack j\rbrack$, where $\beta_{0}\lbrack j\rbrack$ represent the coefficients to be estimated for corresponding input variables. The cumulative hazard, calculated as the product of the hazard function and the semester length ($Len\lbrack j\rbrack$), is used to derive the logarithm of the survival function ($S_{i}\lbrack j\rbrack$) in Equation (2), where $Len\lbrack j\rbrack$ = 1 for all semesters and included here for adaptability in other settings where the academic calendar may be more varied. Finally, the student’s dropout probability in the semester ($\theta_{i}\lbrack j\rbrack$) is calculated as one minus the survival function, as shown in Equation (3). While this model allows us to estimate the influence of each input variable on the hazard function and, subsequently, the dropout probability, it is important to note that it assumes a log-linear relationship between the hazard function and the input variables. To account for potential nonlinear relationships between these variables, we will introduce nonlinearity in our subsequent model. Figure 1 contains a graphic illustration of this PEM model.

$\log\left( h_{i}\lbrack j\rbrack \right) = h_{0}\lbrack j\rbrack + \beta_{0}\lbrack j\rbrack X_{0i}\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(1)

$\log\left( S_{i}\lbrack j\rbrack \right) = - h_{i}\lbrack j\rbrack Len\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(2)

$\theta_{i}\lbrack j\rbrack = 1 - S_{i}\lbrack j\rbrack$ $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(3)

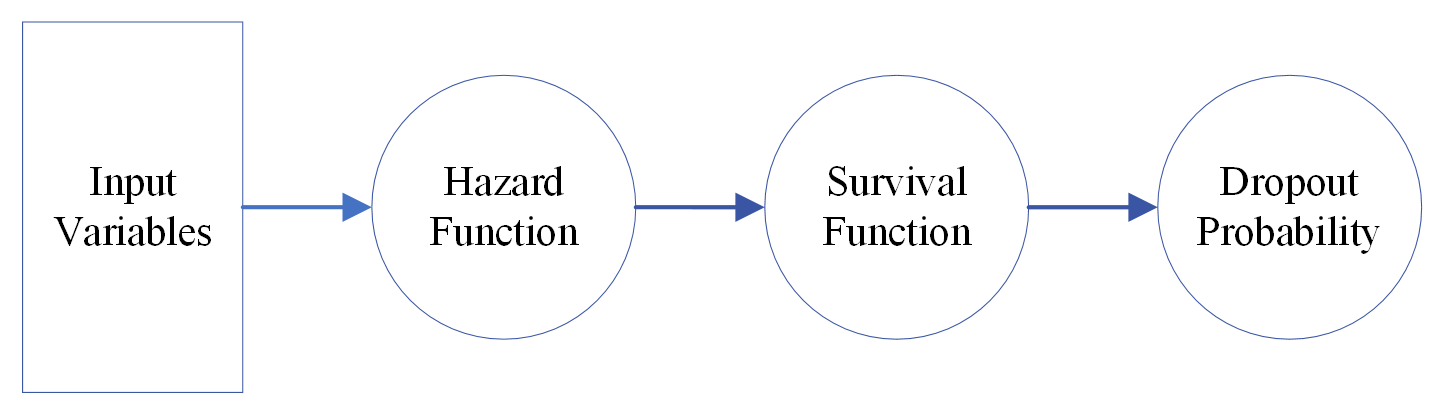
Piecewise Exponential Model with Fully-Connected Neural Network

In this section, we introduce a fully-connected neural network (NN) to estimate the hazard function in a piecewise exponential model; sacrificing interpretability for potentially more predictive power. The hazard function is generated from a hidden layer of neurons in this PEM-NN model as shown in Equation (5), and the hidden neurons are generated from the input variables as shown in Equation (4). The survival function and dropout probability can be calculated in the same way from Equations (2) and (3). Notably, the inclusion of the neural network introduces nonlinearity into the model, driven by the sigmoid activation function (σ) employed in Equation (4). The prediction performance could be improved PEM-NN compared to PEM, because the neural network structure could capture more complex relationships between $X_{0i}\lbrack j\rbrack$ and $h_{i}\lbrack j\rbrack$. However, it’s essential to acknowledge that the PEM-NN model comes with a trade-off. For instance, when identifying a group of students at high risk of dropout, discerning the specific reasons behind this elevated risk becomes intricate. Consequently, devising precise and strategic intervention plans based on the model's output becomes a challenging endeavor. Therefore, we need a model to balance interpretation and prediction. Figure 2 provides a graphical representation of this model for further insights into the PEM-NN model's architecture and visualization.

$$X_{1i}\lbrack j\rbrack = \sigma\left( \alpha_{0}\lbrack j\rbrack + \beta_{1}\lbrack j\rbrack X_{0i}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)$$

$$\log\left( h_{i}\lbrack j\rbrack \right) = h_{0}\lbrack j\rbrack + \beta_{2}X_{1i}\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5)$$

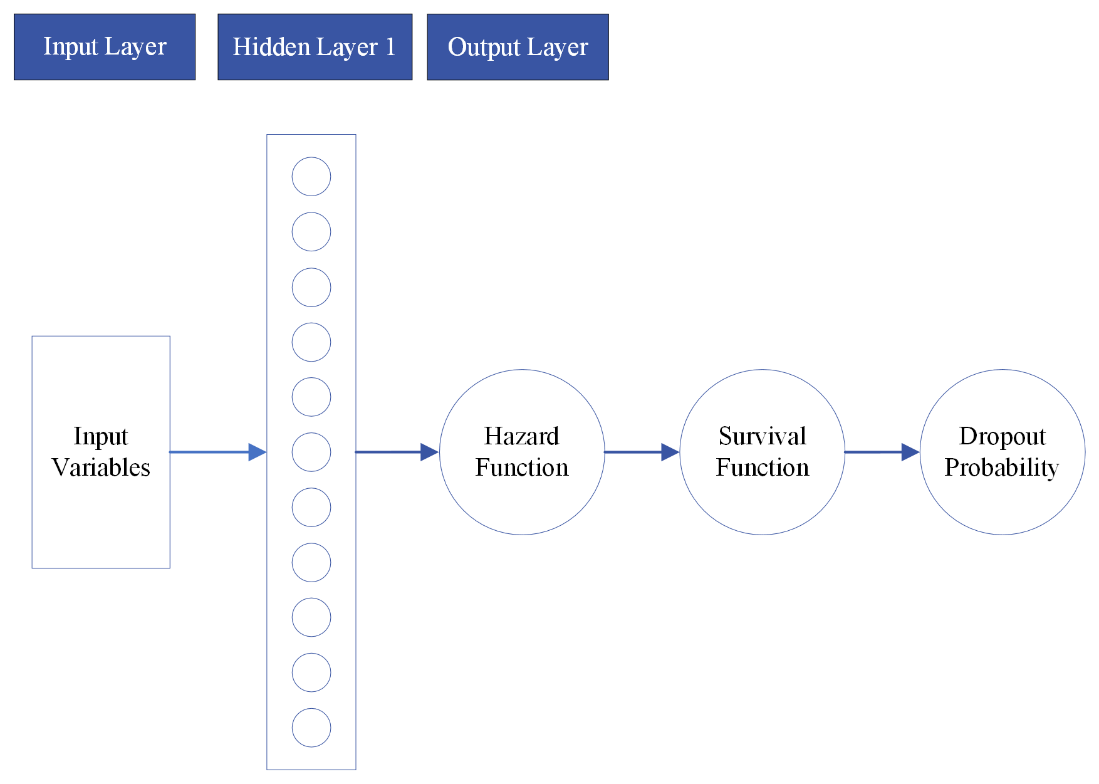
Piecewise Exponential Model with Structural Neural Network

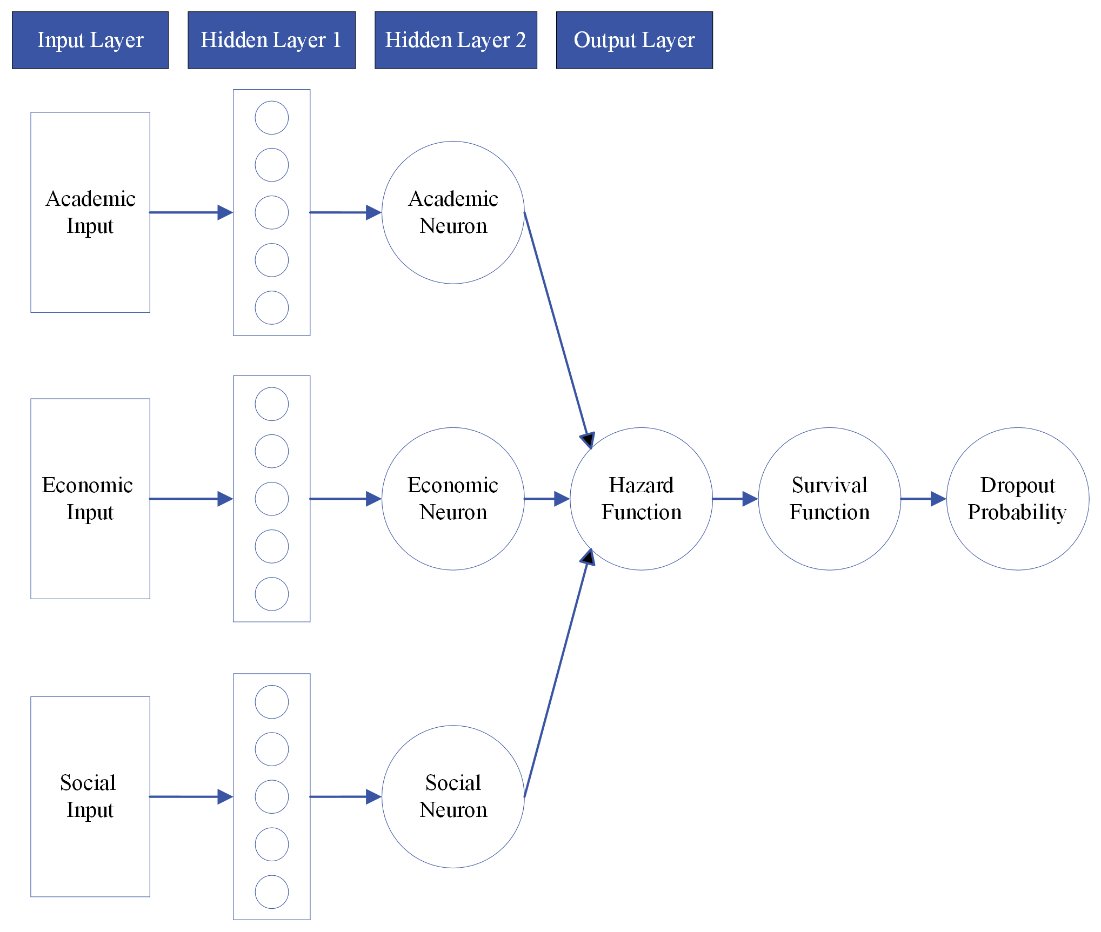
Our proposed new model seeks to balance interpretation and prediction and we design it using a structural neural network (SNN) as follows. In this PEM-SNN model, the input variables $X_{0i}\lbrack j\rbrack$ are grouped into three categories, $X_{0i}^{Acad}\lbrack j\rbrack$ representing academic activities and performance, $X_{0i}^{Econ}\lbrack j\rbrack$ related to financial aid and financial burden, and $X_{0i}^{Socl}\lbrack j\rbrack$ representing family background and demographic characteristics. From the input layer, a hidden layer $X_{1i}^{Acad}\lbrack j\rbrack$ is generated from $X_{0i}^{Acad}\lbrack j\rbrack$ using Equation (6), and an academic neuron $X_{2i}^{Acad}\lbrack j\rbrack$ is then generated from the hidden layer using Equation (7). Similar transformations occur for an economic neuron, $X_{2i}^{Econ}\lbrack j\rbrack$, and a social neuron, $X_{2i}^{Socl}\lbrack j\rbrack$, as shown in Equations (8) to (11). The final three neurons for each integration form the second hidden layer, and the hazard function is the output of the neural network. Equation (12) defines the logarithm of the hazard function $h_{i}\lbrack j\rbrack$ as the sum of the baseline hazard $h_{0}\lbrack j\rbrack$ and a linear combination of the three neurons. The academic integration is represented by $\beta_{2}^{Acad}\lbrack j\rbrack X_{2i}^{Acad}\lbrack j\rbrack$, the economic integration by $\beta_{2}^{Socl}\lbrack j\rbrack X_{2i}^{Socl}\lbrack j\rbrack$, and the social integration by $\beta_{2}^{Socl}\lbrack j\rbrack X_{2i}^{Socl}\lbrack j\rbrack$.

$X_{1i}^{Acad}\lbrack j\rbrack = \sigma\left( \alpha_{0}^{Acad}\lbrack j\rbrack + \beta_{0}^{Acad}\lbrack j\rbrack X_{0i}^{Acad}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(6)

$X_{2i}^{Acad}\lbrack j\rbrack = \sigma\left( \alpha_{1}^{Acad}\lbrack j\rbrack + \beta_{1}^{Acad}\lbrack j\rbrack X_{1i}^{Acad}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(7)

$X_{1i}^{Econ}\lbrack j\rbrack = \sigma\left( \alpha_{0}^{Econ}\lbrack j\rbrack + \beta_{0}^{Econ}\lbrack j\rbrack X_{0i}^{Econ}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(8)

$X_{2i}^{Econ}\lbrack j\rbrack = \sigma\left( \alpha_{1}^{Econ}\lbrack j\rbrack + \beta_{1}^{Econ}\lbrack j\rbrack X_{1i}^{Econ}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(9)

$X_{1i}^{Socl}\lbrack j\rbrack = \sigma\left( \alpha_{0}^{Socl}\lbrack j\rbrack + \beta_{0}^{Socl}\lbrack j\rbrack X_{0i}^{Socl}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(10)

$X_{2i}^{Socl}\lbrack j\rbrack = \sigma\left( \alpha_{1}^{Socl}\lbrack j\rbrack + \beta_{1}^{Socl}\lbrack j\rbrack X_{1i}^{Socl}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$(11)

$$\log\left( h_{i}\lbrack j\rbrack \right) = h_{0}\lbrack j\rbrack + \beta_{2}^{Acad}\lbrack j\rbrack X_{2i}^{Acad}\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$+ \beta_{2}^{Econ}\lbrack j\rbrack X_{2i}^{Econ}\lbrack j\rbrack + \beta_{2}^{Socl}\lbrack j\rbrack X_{2i}^{Socl}\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ (12)$$

Figure 3 illustrates the structure of the hybrid model. The input layer consists of three blocks of variables, which are described in detail in Section 3. The academic input block comprises thirteen variables, the economic input block includes six variables, and the social input block contains nine variables. Each input block generates an individual block of neurons in the first hidden layer. The second hidden layer consists of three neurons in total, with each neuron representing one integration: academic, economic, and social. These neurons serve as the intermediate representation of the input variables before generating the hazard function.

The output layer represents the hazard function, which, in turn, generates the survival function and dropout probability using Equations (2) and (3). It’s important to note that the input variables for different integrations do not interact with each other until the process of generating the hazard function. By enforcing this structured design, we ensure that the interactions among input variables are captured at the appropriate stage and thus we are able to easily interpret which category of variables contribute the most to the prediction. If we were to remove this designed structure and allow all input variables to interact with each other from the beginning, the structural neural network would resemble the more traditional fully connected neural network. Conversely, if we were to remove the two hidden layers and directly generate the hazard function as a linear combination of all input variables, this hybrid model would reduce to the simpler piecewise exponential model.

We implement this sparsely connected neural network structure using the Flux package (v0.13.14) (Innes et al., 2018) in Julia. In a nutshell, the whole network structure is a “chain” in Flux, which is “joined” by six sub-chains, each for one semester. In a chain for a semester, three individual chains are used to transform the three groups of input variables into three neurons, and the three neurons generate the hazard function neuron. Actual model code can be found at https://github.com/Farlein/College_Dropout/tree/main.

Constructing the Loss Function

Suppose student $i$ was enrolled in semester $j$ with input variables $X_{0i}\lbrack j\rbrack$, the loss function in a piecewise exponential model depends on whether the student dropped out by the end of the semester:

$$L_{i}\lbrack j\rbrack = \left\{ \begin{matrix} - S_{i}\lbrack j\rbrack & \left( \text{Retained} \right) \\ - S_{i}\lbrack j\rbrack h_{i}\lbrack j\rbrack & \left( \text{Dropout} \right) \\ \end{matrix} \right.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13)$$

We can write the two cases in one equation. Let $y_{i}$ be the dependent variable, with 1 indicating a student dropped out and 0 indicating the student remained enrolled in the next semester. The loss function can be written as

$$L_{i}\lbrack j\rbrack = - h_{i}^{y_{i}}\lbrack j\rbrack S_{i}\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14)$$

Therefore, the logarithm of the loss function is

$\ logL_{i}\lbrack j\rbrack = - y_{i}\lbrack j\rbrack\log\left( h_{i}\lbrack j\rbrack \right) - \log\left( S_{i}\lbrack j\rbrack \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$

Following from Equations (2) and (1), the logarithm of the loss function can be rewritten as:

$$\ \ \ \ \ \ \ \ \ logL_{i}\lbrack j\rbrack = - y_{i}\lbrack j\rbrack\log\left( h_{i}\lbrack j\rbrack \right) + h_{i}\lbrack j\rbrack L\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$\ \ \ \ \ \ = - y_{i}\lbrack j\rbrack\left( h_{0}\lbrack j\rbrack + \beta\lbrack j\rbrack X_{0i}\lbrack j\rbrack \right) + \exp\left( h_{0}\lbrack j\rbrack + \beta\lbrack j\rbrack X_{0i}\lbrack j\rbrack \right)Len\lbrack j\rbrack\ \ \ \ \ \ (15)$$

Where $Len\lbrack j\rbrack$ is the length of semester $j$ and is set to be 1 for all semesters, regardless of some semesters may last slightly longer than the others. Our dependent variable is imbalanced, because less than 4% of students would drop out in a semester for those who spent their time for at most three years at UD. To address this challenge, we add a hyperparameter $w$ to the loss function to make the dropout observations weight more than the others, so the logarithm of loss function becomes

$\log L_{i}\lbrack j\rbrack = - w*y_{i}\lbrack j\rbrack\left( h_{0}\lbrack j\rbrack + \beta\lbrack j\rbrack X_{0i}\lbrack j\rbrack \right) + \exp\left( h_{0}\lbrack j\rbrack + \beta\lbrack j\rbrack X_{0i}\lbrack j\rbrack \right)Len\lbrack j\rbrack\ \ \$(16)

For the PEM-NN models, using Equations (4) and (5) to derive $h_{i}\lbrack j\rbrack$, the loss function becomes

$$\ logL_{i}\lbrack j\rbrack = - w*y_{i}\lbrack j\rbrack\log\left( h_{i}\lbrack j\rbrack \right) + h_{i}\lbrack j\rbrack Len\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$= - w*y_{i}\lbrack j\rbrack\left( h_{0}\lbrack j\rbrack + \beta_{2}X_{1j} \right) + \exp\left( h_{0}\lbrack j\rbrack + \beta_{2}X_{1j} \right)Len\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$= - w*y_{i}\lbrack j\rbrack\left( h_{0}\lbrack j\rbrack + \beta_{2}\sigma\left( \alpha_{0}\lbrack j\rbrack + \beta_{1}\lbrack j\rbrack X_{0i}\lbrack j\rbrack \right) \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$+ \exp\left( h_{0}\lbrack j\rbrack + \beta_{2}\sigma\left( \alpha_{0}\lbrack j\rbrack + \beta_{1}\lbrack j\rbrack X_{0i}\lbrack j\rbrack \right) \right)Len\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (17)$$

For the PEM-SNN models, using Equation (12), the loss function becomes

$$\log L_{i}\lbrack j\rbrack = - w*y_{i}\lbrack j\rbrack\log\left( h_{i}\lbrack j\rbrack \right) + h_{i}\lbrack j\rbrack Len\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$= - w*y_{i}\lbrack j\rbrack(h_{0}\lbrack j\rbrack + \beta_{2}^{Acad}\lbrack j\rbrack X_{2i}^{Acad}\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$+ \beta_{2}^{Econ}\lbrack j\rbrack X_{2i}^{Econ}\lbrack j\rbrack + \beta_{2}^{Socl}\lbrack j\rbrack X_{2i}^{Socl}\lbrack j\rbrack)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$$+ exp(h_{0}\lbrack j\rbrack + \beta_{2}^{Acad}\lbrack j\rbrack X_{2i}^{Acad}\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$+ \beta_{2}^{Econ}\lbrack j\rbrack X_{2i}^{Econ}\lbrack j\rbrack + \beta_{2}^{Socl}\lbrack j\rbrack X_{2i}^{Socl}\lbrack j\rbrack)Len\lbrack j\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (18)$

Where $X_{2i}^{Acad}\lbrack j\rbrack$, $X_{2i}^{Econ}\lbrack j\rbrack$ and $X_{2i}^{Socl}\lbrack j\rbrack$ are derived from Equations (6) to (11).

Model Training and Evaluation

To predict student dropouts in a semester, we begin by partitioning the data into training and test sets. Specifically, 90% of the data from before the semester under consideration, organized by student ID, is allocated to the training dataset, while the remaining 10% is held out for further analysis of the trained models. The data pertaining to the semester in question constitutes our test dataset. We then employ a systematic three-step process. The first step is hyperparameter tuning. The PEM models require a weight hyperparameter denoted as $w$ in the loss function, while the PEM-NN and PEM-SNN models necessitate the specification of $w$ and the number of neurons within the hidden layers. To ascertain these values, we employ a ten-fold cross-validation procedure on the training dataset. In our case, $w$ is set to 1.4, giving higher weight to dropout observations in the loss function. For the hidden layer of the PEM-NN models, we fix the number of neurons at 11. In the case of the PEM-SNN models, which include three separate groups of neurons (one from each group of variables), we set the number of neurons to 11 for each group.

In the second step, we train our models using the entire training dataset, incorporating the hyperparameter values obtained in the previous step. Following the training, we calculate the hazard function, survival function, and dropout probability, utilizing Equations (1) to (3). Subsequently, we need to establish threshold probabilities to make binary predictions on whether a student will dropout. If the predicted dropout probability surpasses a given threshold, the outcome is predicted as 1 (dropout); otherwise, it is classified as 0 (retained). Given the variations in dropout probability prediction based on the progress in students’ academic careers, we determine six distinct threshold probabilities. This is because, for the same dropout probability, a student may be predicted to dropout if they are in their first semester but not in their sixth, or vice versa. We employ grid search to identify the optimal threshold probabilities.

In the final step, we apply the trained models along with the selected threshold probabilities to the test dataset to make predictions. During the testing stage, we assess the models’ predictive performance using the F1-score metric. The F1-score is the harmonic mean of precision and recall, where a higher precision implies a higher proportion of interventions directed towards students who truly require help and a higher recall indicates that a larger proportion of dropout students would be covered by the interventions. The PEM-Linear model is run once using an Ipopt solver in a Julia package JuMP (v1.10.0) (Lubin et al. 2023), while PEM-NN and PEM-SNN models are run 30 times using a Julia package Flux (v0.13.14) (Innes et al. 2018) using Adam optimization algorithm with a learning rate of 0.01, and the exponential decay rates for the first-momentums and second-momentums are 0.9 and 0.999. This distinction was necessary because a global optimization could only be found for the PEM-Linear model. For each student in the test dataset, a student is predicted to have high dropout risk if more than half of the runs (i.e., more than 15 runs) indicate the student will dropout. We calculate the F1-score based on the predictions and the actual outcomes. Additionally, we conduct a comparative analysis involving the three PEM-related models (PEM-Linear, PEM-NN, and PEM-SNN) and five cross-sectional models: Ridge Logistic Regression (Ridge), Lasso Logistic Regression (Lasso), CART decision tree (CART), Random Forest (RF) and XGBoost decision tree. Unlike survival analysis, which considers a student’s academic trajectory as a continuous, longitudinal process, these cross-sectional methods treat each semester of a student's academic career as an independent event. The first three models, Ridge, Lasso, and CART, offer inherent interpretability, similar to survival analysis models. In contrast, the latter two models, RF and XGBoost, are based on ensemble learning and typically require post hoc interpretation techniques. The cross-sectional models are constructed using well-established R packages with their default settings. We also perform 30 runs for each cross-sectional model to obtain an average prediction performance. Ridge Logistic Regression and Lasso Logistic Regression models are built using a R package glmnet (4.1-8) with regularization parameters selected from 10-fold cross-validation, CART models are built using a R package rpart (v4.1.21), Random Forest models are built using a R package randomForest (v4.7-1.1) with 500 trees and each tree has 5 input variables, and XGBoost is built using a R package gbm (v2.1.8.1) with ten-fold validation to select the best model.

Results and Discussion

Predictive Performance

Table 2 presents a comparison of eight models with respect to their F1-scores for predicting dropout students during the Spring semesters of 2020, 2021, and 2022. These models include three PEM-related models (PEM-Linear, PEM-NN, and PEM-SNN) and five cross-sectional models (Ridge, Lasso, CART, RF, and XGBoost). For all three Spring semesters, it's important to note that Lasso fails to converge, and CART classifies all students as enrolled, rendering their F1-scores unavailable. In Spring 2020, the model with the highest F1-score is XGBoost (0.189), followed by PEM-SNN (0.172), PEM-NN (0.164), PEM-Linear (0.163), RF (0.138), and Ridge (0.126). In Spring 2021, PEM-Linear exhibits the highest F1-score (0.233), followed by PEM-SNN (0.193), XGBoost (0.183), PEM-NN (0.144), Ridge (0.122), and RF (0.091). In Spring 2022, XGBoost again achieves the highest average F1-score (0.266), followed by PEM-SNN (0.247), Ridge (0.246), PEM-NN, PEM-Linear (0.244), PEM-NN (0.227), and Ridge (0.224). Thus, it becomes evident that PEM-SNN demonstrates good predictive performance compared to other PEM-related models and cross-sectional models, consistently ranking as the second-best performer across all three years, highlighting its robustness and potential as a predictive tool for identifying students at risk of dropout. Although XGBoost generally exhibits superior predictive performance, our PEM-SNN model provides easier interpretability, due to its structured design that categorizes predictors.

The F1-scores obtained in our study are lower than those reported in related works on student retention and dropout (e.g., Ameri et al., 2016; Aulck et al., 2019; Baranyi et al., 2020; Manrique et al., 2019; Sandoval-Palis et al., 2020). We attribute these lower scores to the imbalanced nature of our dependent variable. Generally, the rarer the target outcome, the more challenging it is to achieve high predictive performance. For instance, in Manrique et al., the dropout rate is 13.6% (three times higher than our dataset) and their F1-scores ranged from 0.5 to 0.78, while in Sandoval-Palis et al. the dropout rate is 72.8% (eighteen times higher than our dataset) and their F1-score is 0.85, confirming the impact of data imbalance on predictive performance.

The subsequent sections of this chapter will focus on the results derived from the PEM-SNN models. Table 3 shows the F1-scores obtained from the PEM-SNN models for various student groups during the Spring semesters of 2020, 2021, and 2022. The F1-scores exhibit variations among different student groups. In Spring 2020, among students from different cohorts, those in their 6th semester achieve the highest F1-score (0.196), followed by students in their 2nd semester (0.187), and those in their 4th semester (0.128). However, as we progress to Spring 2021 and 2022, the F1-scores exhibit a declining trend as students advance in their academic careers. Specifically, students in their 2nd semester consistently exhibit the highest F1-scores, while those in their 6th semester consistently exhibit the lowest. Moreover, we analyze the performance of the PEM-SNN models concerning two student attributes, Gender (Male and Female) and Pell Grant eligibility. We use these two factors as examples to check whether the models perform similarly for students with different demographic characteristics and socio-economic status. In Spring 2020 and Spring 2021, F1-scores for female students are lower than those for male students, but this pattern reverses in Spring 2022. In contrast, the results for Pell Grant recipients remain consistent over the three Spring semesters, with F1-scores consistently higher for Pell Grant recipients compared to non-Pell students. These findings, i.e., that predictive performance varies among student groups, are similar with what was reported by Wagner et al. (2023) and further study is needed to understand the cause of the difference.

Contribution of the Three Integrations

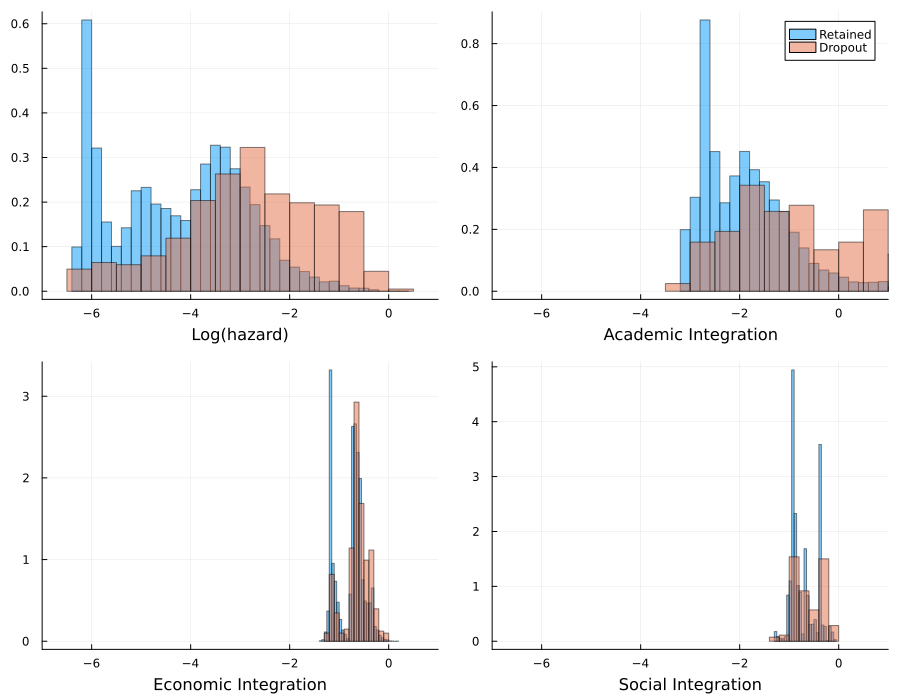
The neural network structure of the PEM-SNN models allows us to dissect the contribution of each group of variables to dropout prediction. We use the results from Spring 2022’s PEM-SNN models as an illustrative example to interpret these contributions. Figure 4 visually represents histograms of the predicted logarithm of hazard (log(h)) alongside the corresponding academic integration, economic integration, and social integration. The x-axes represent log(h), academic integration, economic integration, and social integration, respectively. The y-axes represent the normalized count (i.e., probability density) of each column. The scale of y-axis varies for each sub-figure, because the distribution of the underlying metric varies. A lower scale of y-axis indicates a sparser distribution, e.g., log(h) and academic integration, and a higher scale of y-axis indicates a more concentrated distribution, e.g., economic integration and social integration. In these histograms, log(h) represents the sum of a baseline hazard and the three integrations according to Equation (12), while the integrations are derived from individual groups of variables following Equations (6) to (11). These values are averaged across 30 runs.

Two key observations emerge from these histograms. First, the PEM-SNN models generate distinct distributions of log(h) for retained and dropout students. Log(h) values for retained students tend to be smaller than those for dropout students, aligning with the logic that smaller log(h) values correspond to lower dropout probabilities. Second, the academic integration emerges as the most influential factor in distinguishing between retained and dropout students. Similar to log(h), the distributions of academic integrations differ between the two groups, with academic integrations of retained students generally being smaller than those of dropout students. In contrast, the distributions of economic and social integrations exhibit significant overlap between retained and dropout students, suggesting that these two integrations contribute less to dropout prediction. These observations hold true for Spring 2020 and Spring 2021 as well. However, it’s important to note that while this analysis provides insight into the relative importance of these integrations, it doesn’t offer sufficient information for colleges to design customized intervention plans to reduce students’ dropout risks. It merely indicates that academic integration plays a crucial direct role in predicting high dropout risk; the extent to which academic struggles arise from other factors, such as financial stress or a lack of social support, is not estimatable in this model (Cohausz et al. 2023).

Tracking At-Risk Students

In addition to predicting student dropout in the test dataset, we also apply the trained PEM-SNN models to the hold-out dataset to observe typical patterns of dropout probabilities. As explained in Section 4, the hold-out dataset comprises approximately 10% of data from all available semesters leading up to the semester of the test dataset. On average, the dropout probabilities for retained students are approximately 0.013, while dropout students exhibit an average probability of 0.101. Interestingly, many dropout students have predicted probabilities of zero for all semesters in the hold-out dataset, indicating that they initially appear likely to continue their enrollment but subsequently experience a dramatic decline in their academic performance, leading to dropout. For those dropout students with predicted probabilities higher than zero, many of them have at least one semester with a high dropout risk (dropout probability > 0.5), irrespective of whether it is their last semester or not. These findings highlight the dynamic nature of dropout risk, where students' circumstances and risks can change over time.

Limitations and Future Work

Our study is constrained by several limitations. First, this study is limited to a single educational institution and covers data from Fall 2012 to Spring 2022. As a result, the findings may not be directly applicable to other institutions or different time periods. Dropout risks at other institutions may be directly influenced by economic or social factors. It is essential to exercise caution when generalizing the results beyond the scope of this study. Second, we do not differentiate between students who drop out entirely from higher education and those who transfer to another institution. These two groups of students may have varying reasons for leaving their current institution. Building separate models to predict dropout risks for each group could potentially enhance predictive performance and provide more nuanced insights into the specific causes of attrition. Third, similar to the findings of Wagner et al. (2023), our models exhibit differential performance in predicting dropout risks for various student subpopulations, such as gender and Pell Grant eligibility. This suggests that the models may not be equally effective in identifying at-risk students across all demographic or socioeconomic groups, highlighting the need for further investigation and model refinement. Fourth, the imbalance in our dataset, stemming from the rarity of dropout cases, poses significant challenges to achieving more accurate predictions, as evidenced by the relatively low F1-scores.

Future research can address these limitations and explore several avenues for improvement. First: modifying the input variables and network structure of the PEM-SNN models to investigate which academic variable(s) contribute more significantly to the academic integration. This analysis can help identify the specific academic metrics that exert a more substantial influence on dropout risk. By pinpointing these metrics, institutions can focus their monitoring efforts on areas that have a higher impact on student outcomes. Second: extending the analysis to explore how economic and social factors affect the prediction of academic integration. Understanding the interactions between economic and social factors and their influence on academic integration can provide valuable insights. For instance, recognizing that first-generation college students may face unique challenges and have distinct risk factors can inform targeted interventions and support programs. Third: validating the developed models on datasets from different institutions or time periods to assess their generalizability. This external validation can help determine the extent to which the models' predictive capabilities hold across diverse educational settings. Fourth: developing tailored models for specific student subpopulations, acknowledging that different demographic or socioeconomic groups may exhibit distinct risk profiles. By customizing models to these groups, institutions can enhance their ability to identify and support at-risk students effectively.

Conclusion

In this study, we have introduced a hybrid model, PEM-SNN, which combines a structural neural network with a piecewise exponential model, with the goal of addressing student attrition in colleges. Our hybrid model not only shows the potential to robustly identify the students at high risk of dropout but also provides insights into the direct contributions of academic, economic, and social factors. We applied the model to predict dropout occurrences during the Spring semesters of 2020, 2021, and 2022 at the University of Delaware. The results consistently demonstrated that the PEM-SNN model exhibits the 2^nd best predictive performance compared to two other PEM-related models and five cross-sectional models while providing enhanced interpretability. This indicates that the PEM-SNN model is a valuable tool for the student advising team, providing a list of at-risk students who require focused attention and support.

Among the three integrations incorporated into our model, academic integration emerged as the most influential factor in distinguishing between dropout and retained students, as evidenced by the results generated by the PEM-SNN models. Retained students tended to have lower academic integration values compared to dropout students, resulting in reduced hazard and, consequently, lower dropout probabilities. In contrast, economic and social integrations displayed similar distributions between dropout and retained students, suggesting that they do not directly contribute to dropout prediction. However, it is important to note that these economic and social factors may be very important through the indirect impact they have on academic performance. Thus, it remains important to consider a holistic approach when designing customized intervention plans for at-risk students, taking into account the interconnected nature of these factors.

In conclusion, our hybrid model, PEM-SNN, represents a valuable tool in the ongoing effort to reduce student attrition in higher education. By leveraging predictive analytics, institutions can identify at-risk students early and enabling timely interventions to enhance student success and retention. However, it is essential to continue refining and expanding these models, taking into account the unique characteristics of different institutions and student populations. Ultimately, such efforts can contribute to higher graduation rates and improved educational outcomes for all students.

Declaration of generative AI software tools in the writing process

During the preparation of this work, the authors used ChatGPT in all sections in order to improve the readability and clarity of this paper. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

References

1. Agarwal, R., Melnick, L., Frosst, N., Zhang, X., Lengerich, B., Caruana, R. and Hinton, G.E. 2021. Neural additive models: Interpretable machine learning with neural nets. Advances in neural information processing systems, 34, 4699-4711.
2. Aina, C., Baici, E., Casalone, G. and Pastore, F. 2022. The determinants of university dropout: A review of the socio-economic literature. Socio-Economic Planning Sciences, 79, 101102.
3. Albreiki, B., Zaki, N., and Alashwal, H. 2021. A systematic literature review of student’ performance prediction using machine learning techniques. Education Sciences 11, 9, 552.
4. Almarabeh, H. 2017. Analysis of students’ performance by using different data mining classifiers. International Journal of Modern Education and Computer Science 9, 8, 9.
5. Ameri, S., Fard, M. J., Chinnam, R. B., and Reddy, C. K. 2016. Survival analysis based framework for early prediction of student dropouts. In Proceedings of the 25th ACM International on Conference on Information and Knowledge Management. Association for Computing Machinery, New York, NY, USA, 903–912.
6. Aulck, L., Nambi, D., Velagapudi, N., Blumenstock, J., and West, J. 2019. Mining university registrar records to predict first-year undergraduate attrition. In Proceedings of the 12th International Conference on Educational Data Mining (EDM 2019), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, 9–18.
7. Aulck, L., Velagapudi, N., Blumenstock, J., and West, J. 2016. Predicting student dropout in higher education. arXiv preprint, arXiv:1606.06364.
8. Baker, R. S. and Yacef, K. 2009. The state of educational data mining in 2009: A review and future visions. Journal of Educational Data Mining 1, 1, 3–17.
9. Baranyi, M., Nagy, M. and Molontay, R. 2020, October. Interpretable deep learning for university dropout prediction. In Proceedings of the 21st annual conference on information technology education. Association for Computing Machinery, New York, NY, USA, 13-19.
10. Bean, J. P. 1980. Dropouts and turnover: The synthesis and test of a causal model of student attrition. Research in Higher Education 12, 155–187.
11. Bouchrika, I. 2023. College dropout rates: 2023 statistics by race, gender & income. https://research.com/universities-colleges/college-dropout-rates Accessed: 12-05-2023.
12. Cai, C. and Fleischhacker, A. 2022. The effect of loan debt on graduation by department: A Bayesian hierarchical approach. Journal of Student Financial Aid 51, 2, Article 5.
13. Cannistra, M., Masci, C., Ieva, F., Agasisti, T., and Paganoni, A. M. 2022. Early-predicting dropout of university students: An application of innovative multilevel machine learning and statistical techniques. Studies in Higher Education 47, 9, 1935–1956.
14. Cohausz, L. 2022. Towards Real Interpretability of Student Success Prediction Combining Methods of XAI and Social Science. In Proceedings of the 15th International Conference on Educational Data Mining (EDM 2022), A. Mitrovic and N. Bosch, Eds. International Educational Data Mining Society, 361–367.
15. Cohausz, L., Tschalzev, A., Bartelt, C. and Stuckenschmidt, H. 2023. Investigating the Importance of Demographic Features for EDM-Predictions. In Proceedings of the 16th International Conference on Educational Data Mining (EDM 2023), M. Feng, T. Käser and P. Talukdar, Eds. International Educational Data Mining Society, 125–136.
16. Deike, R.C. 2003. A study of college student graduation using discrete-time survival analysis. Ph.D. thesis, The Pennsylvania State University.
17. Durkheim, E. 2005. Suicide: A study in sociology. Routledge.
18. Fan, J., Ke, Z. T., Liao, Y., and Neuhierl, A. 2022. Structural deep learning in conditional asset pricing. Available at SSRN: https://ssrn.com/abstract=4117882 or http://dx.doi.org/10.2139/ssrn.4117882.
19. Friedman, M. 1982. Piecewise exponential models for survival data with covariates. The Annals of Statistics 10, 1, 101–113.
20. Heredia-Jimenez, V., Jimenez, A., Ortiz-Rojas, M., Marín, J. I., Moreno-Marcos, P. M., Muñoz-Merino, P. J., and Kloos, C. D. 2020. An early warning dropout model in higher education degree programs: A case study in Ecuador. In Proceedings of the Workshop on Adoption, Adaptation and Pilots of Learning Analytics in Under-represented Regions co-located with the 15th European Conference on Technology Enhanced Learning (LAUR@ EC-TEL 2020). P. J. M. Merino, C. D. Kloos, Y.-S. Tsai, D. Gasevic, K. Verbert, M. Perez-Sanagustin, I. Hilliger, M. A. Z. Prieto, M. Ortiz-Rojas and E. Scheihing, Eds. 58–67.
21. Innes, M., Saba, E., Fischer, K., Gandhi, D., Rudilosso, M. C., Joy, N. M., Karmali, T., Pal, A., and Shah, V. 2018. Fashionable modelling with flux. arXiv preprint arXiv:1811.01457.
22. Köhler, M. and Langer, S. 2021. On the rate of convergence of fully connected deep neural network regression estimates. The Annals of Statistics 49, 4, 2231–2249.
23. Kopper, P., Pölsterl, S., Wachinger, C., Bischl, B., Bender, A. and Rügamer, D. 2021, May. Semi-structured deep piecewise exponential models. In Proceedings of AAAI Spring Symposium on Survival Prediction - Algorithms, Challenges, and Applications (2021), R. Greiner, N. Kumar, T. A. Gerds, M. van der Schaar, Eds. PMLR, 40–53.
24. Kopper, P., Wiegrebe, S., Bischl, B., Bender, A. and Rügamer, D. 2022, May. DeepPAMM: Deep Piecewise Exponential Additive Mixed Models for Complex Hazard Structures in Survival Analysis. In Pacific-Asia Conference on Knowledge Discovery and Data Mining (2022). Springer International Publishing, 249–261.
25. Lubin, M., Dowson, O., Garcia, J. D., Huchette, J., Legat, B., and Vielma, J. P. 2023. JuMP 1.0: Recent improvements to a modeling language for mathematical optimization. Mathematical Programming Computation. Mathematical Programming Computation. 15: 581–589. https://doi.org/10.1007/s12532-023-00239-3.
26. Manrique, R., Nunes, B.P., Marino, O., Casanova, M.A. and Nurmikko-Fuller, T., 2019, March. An analysis of student representation, representative features and classification algorithms to predict degree dropout. In Proceedings of the 9th International Conference on Learning Analytics & Knowledge. Association for Computing Machinery, New York, NY, USA, 401-410.
27. Márquez-Vera, C., Cano, A., Romero, C., Noaman, A. Y. M., Mousa Fardoun, H., and Ventura, S. 2016. Early dropout prediction using data mining: a case study with high school students. Expert Systems, 33: 107–124. doi: 10.1111/exsy.12135.
28. National Center for Education Statistics (NCES). 2022. Undergraduate retention and graduation rates. https://nces.ed.gov/programs/coe/indicator/ctr Accessed: 05-22-2023
29. Quadri, M. and Kalyankar, D. N. 2010. Drop out feature of student data for academic performance using decision tree techniques. Global Journal of Computer Science and Technology 10, 2, 2–5.
30. Raisman, N. 2013. The cost of college attrition at four-year colleges & universities-an analysis of 1669 US institutions. Policy perspectives.
31. Sandoval-Palis, I., Naranjo, D., Vidal, J., and Gilar-Corbi, R. 2020. Early dropout prediction model: A case study of university leveling course students. Sustainability 12, 22, 9314.
32. Schmidt-Hieber, J. 2020. Nonparametric regression using deep neural networks with ReLU activation function. Annals of Statistics, 48, 4, 1875–1897. https://doi.org/10.1214/19-AOS1875
33. Schneider, M. 2010. Finishing the first lap: The cost of first year student attrition in America’s four-year colleges and universities. Presented in the 50^th annual Meeting of the Association for Institutional Research (AIR 2010).
34. Spady, W. G. 1970. Dropouts from higher education: An interdisciplinary review and synthesis. Interchange 1, 1, 64–85.
35. Stage, F. K. 1989. Motivation, academic and social integration, and the early dropout. American Educational Research Journal 26, 3, 385–402.
36. Stinebrickner, R. and Stinebrickner, T. 2014. Academic performance and college dropout: Using longitudinal expectations data to estimate a learning model. Journal of Labor Economics 32, 3, 601–644.
37. Tinto, V. 1975. Dropout from higher education: A theoretical synthesis of recent research. Review of Educational Research 45, 1, 89–125.
38. Wagner, K., Volkening, H., Basyigit, S., Merceron, A., Sauer, P., and Pinkwart, N. 2023. Which approach best predicts dropouts in higher education? In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023), SCITEPRESS – Science and Technology Publications, 2, 15–26.

Appendices

Appendix A

Table A.1 provides an overview of the headcount flow for the ten cohorts across different semesters. The smallest cohort, Fall 2020, consisted of 3,711 first-time full-time students, while the largest cohort, Fall 2017, comprised 4,258 students. The headcount of each cohort gradually decreased over the semesters due to dropout. Blank cells in the table indicate that the corresponding cohort had not reached that particular semester.

Table A.2 presents the headcounts for each semester between Fall 2012 and Spring 2022, organized by cohort. Each semester featured up to three cohorts: freshman, sophomore, and junior. Senior cohorts were excluded from the analysis as they had already completed their third year or exceeded the sixth semester. The initial semesters do not have three cohorts due to the absence of data before the Fall 2012 cohort.