Abstract
Knowledge tracing aims to model and predict students’ knowledge states during learning activities.
Traditional methods like Bayesian Knowledge Tracing (BKT) and logistic regression have limitations in
granularity and performance, while deep knowledge tracing (DKT) models often suffer from lacking
transparency. This paper proposes a Transformer-based framework that emphasizes both accuracy and
interpretability. It captures the relationship between student behaviors and learning outcomes considering the
associations between exam and exercise problems. We participated in the EDM Cup 2023 Contest using
the proposed framework and achieved first place on the task of predicting students’ performance
on end-of-unit test problems using clickstream data from previous assignments. Furthermore, the
framework provides meaningful insights by analyzing user actions and visualizing attention weight
matrices. These insights enable targeted interventions and personalized support, enhancing online
learning experiences. We have uploaded our code, saved models, and predictions to an OSF repository:
https://osf.io/mdpzc/.
Keywords
1. Introduction
With the growth of online learning platforms such as Massive Open Online Courses (MOOCs) and Intelligent Tutoring Systems (ITS), the need to understand students’ knowledge states and learning needs is becoming more important (Abdelrahman et al., 2023, Sein Minn, 2022). Knowledge tracing is a powerful method in educational data mining that aims to model and predict students’ knowledge states as they engage in learning activities (Piech et al., 2015, Corbett and Anderson, 1994, Abdelrahman et al., 2023). By analyzing students’ responses and interactions with online learning platforms, knowledge tracing seeks to uncover the latent knowledge and skills possessed by each student, and hence gain a better understanding of their learning behaviors.
Previous research in the field of knowledge tracing has explored various approaches. Early attempts primarily focused on Bayesian Knowledge Tracing (BKT) (Corbett and Anderson, 1994). BKT utilizes a student’s prior knowledge of skills to compute the conditional probability of producing correct responses. However, BKT has encountered two main challenges: 1) it represents user state as binary variables, limiting its granularity (Piech et al., 2015), and 2) it can suffer from biased inferences under wrong or missing priors (Baker et al., 2008). Other researchers have employed logistic regression models (Wright, 1995) and factor analysis (Pavlik et al., 2009). The common issue of these approaches is that they are often highly constrained and structured, leading to interpretability advantages but compromised performance.
In recent years, the rapid advancement of deep learning techniques has sparked interest in knowledge tracing. Deep Knowledge Tracing (DKT) (Piech et al., 2015)) is the first attempt to use deep learning for knowledge tracing, which integrates the power of deep learning with knowledge tracing methodologies to achieve more accurate modeling and prediction of students’ knowledge states (Lu et al., 2020). Unlike traditional knowledge tracing methods that rely on handcrafted features, DKT automatically learns representations from raw input data, such as student responses or interaction sequences, allowing for more nuanced and informative representations of student knowledge states. Recently, sequential models such as Recurrent Neural Networks (RNNs) (Medsker and Jain, 2001), Long Short-Term Memory (LSTM) (Hochreiter and Schmidhuber, 1997), and attention (Pandey and Karypis, 2019, Vaswani et al., 2017) have emerged as key types of models used in knowledge tracing. In this paper, we refer to such deep learning knowledge tracing models as DKT models. These deep neural network architectures enable fine-grained and precise predictions of student performance, offering valuable insights for personalized learning, adaptive interventions, and educational decision-making.
While the type of learning outcome varies depending on the purpose of a prediction task, the most popular type of learning outcome is performance classes/grades (Namoun and Alshanqiti, 2021). In many contexts, such performance measures are taken from exam grades (Kőrösi and Farkas, 2020, Moreno-Marcos et al., 2020, Lu et al., 2022). It is natural to assume that problems used in an exam do not appear in any previous assignment. In practice, teachers often intentionally avoid including problems in the final exams that have already appeared in daily assignments to ensure the validity of the assessment. However, such a distinction between exam and exercise problems is not typically made in many knowledge tracing models (Pandey and Karypis, 2019, Piech et al., 2015). This distinction highlights an opportunity for enhancement in the precise prediction of student behaviors and performance during examinations.
Bridging these gaps, we propose a Transformer-based framework for deep knowledge tracing to predict end-of-unit test problems from students’ behavioral interactions with in-unit assignments on a learning platform. Transformer is the transduction model relying entirely on attention to compute representations of sequential data without using RNNs or convolution (Vaswani et al., 2017). We also propose several methods to interpret the model to gain insights into how students’ interactions will affect their future learning outcomes.
To provide more context for our research project, we took part in the EDM Cup 2023 Contest1, where contest participants were asked to predict students’ performance on end-of-unit math problems using their clickstream data from previous assignments. For each student, the end-of-unit tests contain distinct sequences and problems from those in the in-unit assignments. The dataset also contains abundant problem and assignment information, such as word embeddings from the text of problems and curriculum information on assignments. Sometimes, such auxiliary information is not available and often is not incorporated into DKT models such as Piech et al. (2015) and Pandey and Karypis (2019). As the goal of the contest was to maximize the prediction accuracy, we utilized most of the auxiliary information to maximize the prediction accuracy of our model. Therefore, although our framework is related to a self-attentive model for knowledge tracing (SAKT), which uses an attention mechanism (Pandey and Karypis, 2019), it is different from SAKT in many aspects including the distinction between the in-unit and end-of-unit problems and the use of auxiliary information to construct the representations of problems. Table 1 offers a comprehensive comparison of our method with existing knowledge tracing techniques, including Bayesian Knowledge Tracing (BKT) (Corbett and Anderson, 1994), Deep Knowledge Tracing (DKT) (Piech et al., 2015), Exercise-aware Knowledge Tracing (EKT) (Liu et al., 2019), Self-Attentive Knowledge Tracing (SAKT) (Pandey and Karypis, 2019), and Separated Self-AttentIve Neural Knowledge Tracing (SAINT) (Choi et al., 2020). The comparison covers model types, memory length, generalizability, and the distinction between in-unit assignments and end-of-unit tests. For deep learning-based models, we also examined how they construct latent representations and inputs for the attention module.
Briefly speaking, our framework started by creating new features in data pre-processing, and then in our model, we utilized latent embeddings for important variables in the training dataset, such as action types, problems, students, and classes. Finally, we integrated all the information above and used it to train a Transformer Encoder. By doing so, the model could efficiently learn the types of problems and assignments so that the associations between in-unit assignment problems and end-of-unit test problems are more accurately learned. Our model has the best prediction accuracy, as exemplified by the first-place position in the contest with an AUC of 78.969% for the private dataset. Notably, it also achieved the overall best performance considering both the public and the private leaderboard, demonstrating its effectiveness and robustness.
Furthermore, we place a significant emphasis on enhancing the interpretability of our model. It is known that the high accuracy achieved by ”black-box” models, such as deep learning models, often comes at the expense of interpretability due to over-parameterization (Li et al., 2022). Most existing DKT models suffer from the interpretability issue, which has painfully impeded the practical applications of DKT models in the education domain (Lu et al., 2020). Therefore, one of the objectives of this paper is to address this critical issue by introducing a set of model designs that strike a balance between high accuracy and good interpretability and offering several different methods to interpret our models.
We mainly analyzed how students’ interactions with the ITS can affect their learning outcomes and estimated the similarity of interaction types in terms of their effects. We also conducted visualizations of attention weight matrices, where we managed to extract meaningful insights into the underlying factors influencing student performance. These insights have direct practical implications, allowing for targeted interventions and personalized support for individual students. Ultimately, this approach aims to enhance the overall quality of online learning experiences, providing valuable guidance and support to both educators and students.
This work contributes to the literature in the following ways:
- We propose a novel Transformer-based framework for the ASSISTments dataset which integrates several data-preprocessing techniques with a Transformer-based predictive model that predicts students’ responses to end-of-unit test problems from an action log of in-unit problems.
- We maximize the prediction accuracy of the model by incorporating the auxiliary information of problems, sequences, and students. Our model achieved first place on the leaderboard in the EDM Cup 2023 using a test dataset that was not available to the participants during the contest.
- We propose interpretation methods that are specific to our models using the attention weights and keys from the Transformer Encoder. The methods allow us to study the importance of each action type, the effects of each action type, and possibly identify small knowledge components.
| BKT | DKT | EKT | SAKT | SAINT | Ours | ||
|---|---|---|---|---|---|---|---|
| Type of Model | Hidden Markov Model (HMM) | RNN-based (RNN, LSTM) | RNN-based (Bi-directional LSTM) with Attention Mechanism | Transformer-based Encoder model | Transformer-based Encoder-Decoder model | Transformer-based Encoder model | |
| Long-term memory on student interaction history | No | Yes | Yes | Yes | Yes | Yes | |
| Generalizable on sparse data | No | No | Yes | Yes | Yes | Yes | |
| The distinction between in-unit assignments and end-of-unit tests | No | No | No | No | No | Recognizing the distinction by constructing separate vectors for the attention module regarding in-unit assignments (IIU) and end-of-unit tests (IEU) | |
| Latent representations | Problem | - | One-hot encoding when M is small; random Gaussian low-dimensional representation when M is large (M: number of unique exercises); Learned separately for each problem and response (correct/incorrect) pairs | Problem text content embeddings via pretrained model (Word2Vec) | Problem embeddings learned for each problem and response (correct/incorrect) pairs | Problem embeddings learned for each problem and response (correct/incorrect) pairs | Problem embeddings learned for each problem (later combined with action embeddings); Problem features (problem type, BERT-encoded text content, skill code, indicators for multimedia) |
| Sequence | - | No | No | No | No | Sequence embeddings; Sequence level embeddings (units, subjects, etc.) | |
| Action | - | No | No | No | Time-related features (elapsed time, timestamp) | Action type embeddings; Time-related features; Additional action features (tutoring options, number of attempts) | |
| Student and Class | - | No | No | No | No | Student-class matrix + SVD | |
| Inputs for the attention module | - | - | - | Exercise embeddings as queries; interaction embeddings as keys and values | Encoder: Self-attention on exercise embeddings. Decoder: interaction embeddings as queries; encoded exercise embeddings as keys and values | IEU vectors as queries; IIU vectors as keys and values |
2. Dataset
In this study, we focus on analyzing student performance using click-stream data, which captures
students’ interactions with the ASSISTments platform (Heffernan and Heffernan, 2014). The dataset
and details of the features are provided in the Open Science Framework (OSF) repository of the
dataset: https://osf.io/yrwuh/. An overview of the complete dataset is provided
in Figure 1. The dataset comprises 10 dataframes, each containing specific information
about student interactions and performance. Table 2 shows the descriptive statistics of the
dataset.
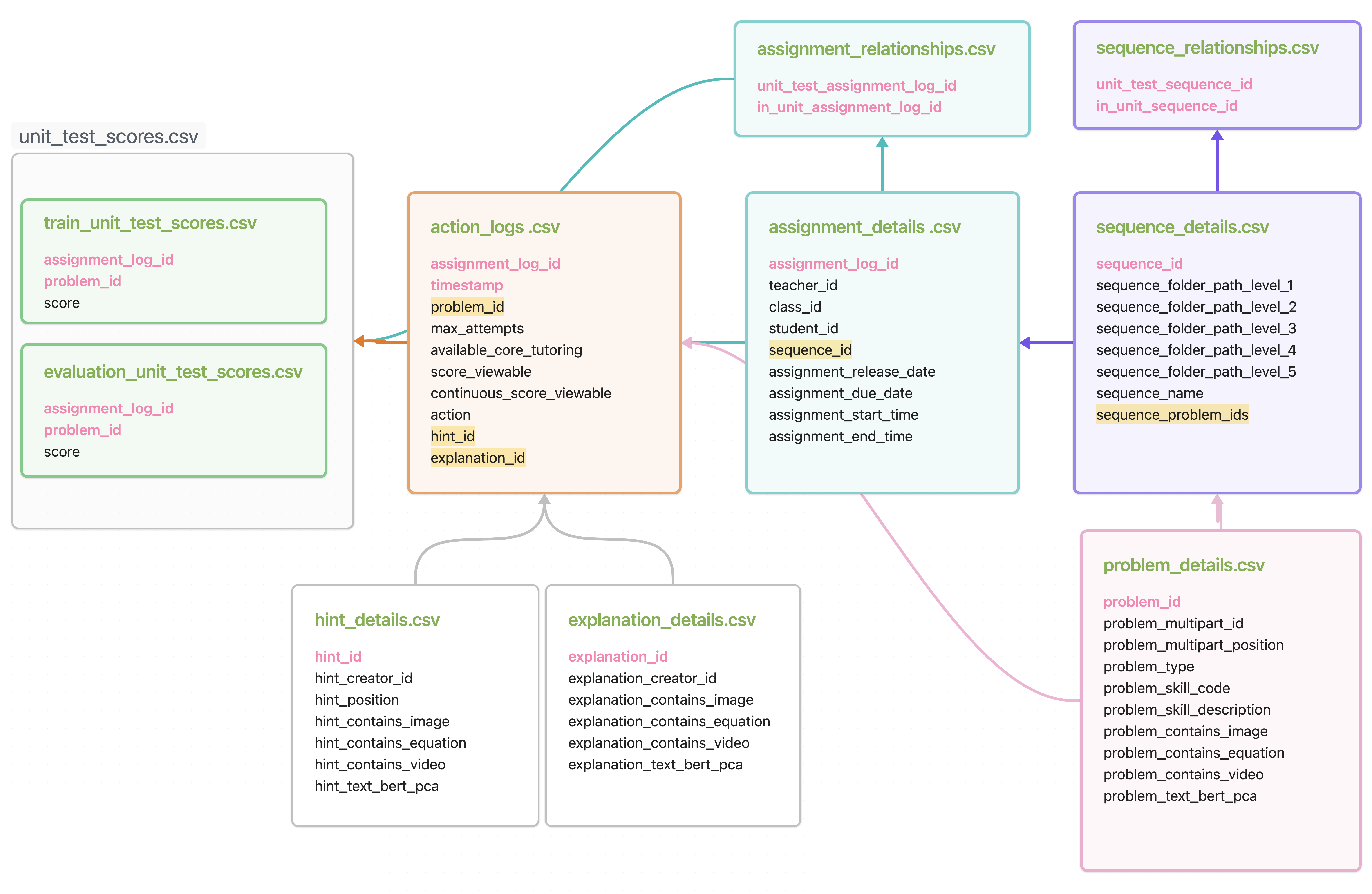
The smallest component in this dataset is a problem. Each problem has a unique problem ID and a multi-part problem ID. Problems that belong to a multi-part problem share the same multi-part ID. Additionally, each problem has six features: problem type, problem text, problem skill code, and binary indicators of whether the problem contains images, equations, or videos, respectively. Problem type indicates the format of the answer to the problem, that is, whether it will be answered by selecting from multiple choices, entering a number, providing an ungraded open response, and so on. Problem text is the first 32 principal components of the BERT embedding for the text-based content of the problem. Problem skill code denotes the type of skill most related to solving the problem.
A list of problems forms a sequence. Unless stated otherwise, when we mention a sequence in this manuscript, it means a sequence of problems. Each sequence contains a unique sequence ID. Sequences are organized into folders with a maximum of five levels. The first level shows whether the sequence came from the Kendall Hunt Illustrative Mathematics curriculum2 or the Engage New York mathematics curriculum3, the second level reveals what grade or subject the sequence is a part of, and the third to fifth level indicates specific unit and subject information.
When a sequence is assigned to a student, it becomes an assignment. A sequence can be assigned multiple times and to multiple students. Each assignment has a unique assignment log ID, a sequence ID, and a student ID. Additionally, each assignment contains the ID of the teacher who assigned the sequence to the student (teacher ID), and the ID of the class that the student attends (class ID). Timestamp attributes are also provided, including the release date, due date, start time, and end time of the assignment.
A sequence can be assigned for two types of purposes. One is the in-unit assignment, which students are supposed to complete during the learning process. The other is the end-of-unit test, which examines students’ learning outcomes. Note that for each student, sequences that appear within the unit and at the end of the unit are distinct. In other words, a student will not be tested with the same set of problems that they have solved in the within-unit assignments.
Another important observation is that the total number of items in Table 2 is typically larger than the sum of the items found in the in-unit assignments and end-of-unit tests. This occurs because only a portion of the total items documented in the original dataset actually appear in the assignments and tests. For instance, the dataframe storing sequence information contains a total of 10,228 sequences, while only 5,259 unique sequences are assigned in the in-unit assignments and 165 in the end-of-unit tests. On the other hand, some items in the in-unit assignments or end-of-unit tests are not documented in the dataframes storing them. As a result, we lack information or features for these items except for their IDs. This discrepancy adds to the challenge of our prediction task, as it introduces missing or incomplete data that we need to account for.
The clickstream data from students, collected as they completed in-unit assignments, are called action logs. The action logs encompass a vast collection of actions that correspond to various types of student interactions during in-unit assignments and are the main source of behavioral data for predicting unit test scores. Each record in the action logs contains an assignment ID, a timestamp, an action type, and several additional features. Specifically, 14 types of actions are recorded, including starting/finishing a problem, making a correct/wrong response, requesting a hint/tutor, etc. For a full list of actions and their descriptions, see Appendix A.
Two additional action features are considered: tutoring options and the maximum number of attempts. Tutoring option refers to which core tutoring option was available at the start of the problem, with one of the four possible values: hint (a set of hints was available upon the student’s request), explanation (an explanation was available upon the student’s request), answer (only the correct answer was available upon the student’s request), and no tutoring (no tutoring was available for this problem at all). The maximum number of attempts, configured by the teacher upon assignment, indicates how many chances a student has for a particular problem before they see they have lost all credit on the problem.
Given all the data described above, our task is to predict how students perform in the end-of-unit tests, i.e., their test scores. The unit test results are divided into two subsets: the training set and the evaluation set. In the training set, the scores are publicly available, allowing us to utilize them as labels for supervised learning. In the evaluation set, for each pair of student IDs and problem IDs, we are required to predict whether the problem has been answered correctly by this student. After that, we submit our predictions to Kaggle for assessment.
| Count | Total | In-Unit Assignments | End-of-Unit Tests
|
|---|---|---|---|
| # sequences | 10,228 | 5,259 | 165 |
| # problems | 132,738 | 57,361 | 1,900 |
| # students | 651,253 | 36,296 | 34,652 |
| # teachers | 23,523 | 2,033 | 1,828 |
| # class | 8,774 | 3,056 | 2,754 |
3. Methods
We have uploaded our code, saved models and predictions to an OSF repository:
https://osf.io/mdpzc/.
3.1. Preprocessing
Since the original dataset is of large scale and contains multiple data files, we did careful preprocessing. We chose action logs as the main dataframe and merged other dataframes by IDs. For categorical features that have more than two options, we use one-hot encoding. We created some additional features, e.g., time since last each action, number of attempts, number of students per class, etc., which we explain in the following sections. We convert text IDs to numeric IDs for the convenience of creating latent embeddings later on.
3.1.1. Generation of New Univariate Features
All the action interactions in the action logs have associated timestamps. The original timestamps are encoded as UNIX time, so we needed to generate several features from it to facilitate efficient learning of deep learning models. First, we generate a feature by calculating the difference between the two consecutive UNIX timestamps. We expect that the model could capture some knowledge about a student from it, such as high-performing students might make faster actions. Second, we generate a feature representing a day by calculating the remainder of the timestamp divided by 8,6400,000 (one day in milliseconds). This feature might help the model identify some patterns of the fluctuation in student performance when they perform in the morning and at night. Third, we generate a feature representing a day in a week by calculating the remainder of the timestamp divided by 86,400,000 times 7. Similarly, this feature might help the model identify a specific group of students who perform badly on a specific day, such as Friday.
3.1.2. Scaling and Standardizing Features
The problem text feature, i.e., the first 32 principal components of the BERT embedding for the text-based content of the problem, was standardized to have a mean of 0 and a standard deviation of 1. In addition, all the features related to timestamps are scaled so that their minimum value is 0 and the maximum value is 1 (min-max scaling). This is because extreme values could be generated if we standardize the feature instead.
3.1.3. Student and Class Embeddings
In predicting student performance, it is useful to use students’ group information to infer their ability. For example, the school districts students belong to are related to their socio-economic status, which is predictive of students’ performance.
The dataset has two features that are related to the groups to which students belong: teachers and classes. Technically speaking, we could use either or both features in the model. However, we decided to use only classes because using both features at the same time will create too much redundancy (e.g., one unique teacher might have only one unique class) and might cause overfitting.
More specifically, let \(\mathbf {S} \in \{0,1\}^{N \times M}\) be a matrix of class memberships for all the students in the dataset where \(N\) is the number of students and \(M\) is the number of classes. Each row of this matrix contains binary indicators representing the class memberships of student \(i\). We can gain a low-rank approximation of \(\mathbf {S}\) by truncated Singular Value Decomposition (SVD):
\begin {align} \mathbf {S} \approx \mathbf {U}\mathbf {\Sigma }\mathbf {V}^T, \end {align}
where \(\mathbf {U} \in \mathbb {R}^{N \times k}\) and \(\mathbf {V} \in \mathbb {R}^{M \times k}\) are a matrix of orthonormal columns, and \(\mathbf {\Sigma } \in \mathbb {R}^{k \times k}\) is a square matrix with the singular values on the diagonal. Here, we treat \(\mathbf {U}\mathbf {\Sigma } \in \mathbb {R}^{N \times k}\) as the student embedding matrix and \(\mathbf {V}\in \mathbb {R}^{M \times k}\) as the class embedding matrix, which are used as pretrained and fixed embeddings in the model. Then, each row of the student and class embedding matrix is the embedding for its corresponding student.
Student and class embeddings can accommodate out-of-vocabulary students to make predictions for them. Suppose \(\mathbf {s} \in \mathbb {R}^M\) is a vector of class memberships for a new student. Then, their student embedding can be obtained simply by \(\mathbf {u} = \mathbf {s}^T \mathbf {V}\). This is because \(\mathbf {S} \mathbf {V} = \mathbf {U}\mathbf {\Sigma }\) and \(\mathbf {V}\) is a matrix with orthogonal columns. If a student only belongs to classes that are not contained in this model, we can simply use a zero vector for their student embedding. Similarly, if we want to add a new class, the class embedding for this new class would be just a zero vector because the past students in the dataset would not have taken this class.
3.1.4. Using a Subset of Action Types
Appendix A presents the complete list of action types recorded in the action log. For our analysis, we only included the following action types: “assignment started,” “correct response,” “wrong response,” “open response,” “answer requested,” “hint requested,” “explanation requested,” “skill related video requested,” and “live tutor requested.” Note that all these action types except for “assignment started” are associated with a specific problem. We included “assignment started” to possibly indicate that students started an assignment but did not make any action for any in-unit problems, yet solved some end-of-unit test problems. This selection of action types was based on our preliminary analysis, which indicated that the inclusion of such a subset of action types did not influence the prediction results, suggesting that the excluded action types are not critical for prediction purposes. By omitting insignificant action types, we aim to simplify the data for easier interpretation and expedite the model training process.
3.2. Model Architecture
Figure 2 illustrates the architecture of our model. In this model, we adopt the core components of
the Transformer Encoder, which includes multi-layer perceptrons (MLPs) and attention mechanisms. In
addition, we extend the basic Transformer encoder structure by incorporating additional
components to address the specific requirements of our task. The model is implemented using
PyTorch (Paszke et al., 2019), an open-source machine learning library for
developing neural-network-based models.
3.2.1. Embedding Layer
The embedding layer transforms input tokens or sequences into continuous vector representations, known as embeddings. It serves as the initial stage of the model, converting discrete input elements into continuous representations that capture their semantic meaning and contextual information. Specifically, we use embedding layers to map IDs (problem IDs, sequences IDs, sequence folder paths, and action type IDs) from one-hot encoded representations into dense embedding vectors. The weights of the embedding layer are initialized randomly and will be iteratively refined and updated via backpropagation throughout the training process. Note that the model is designed without a predefined maximum input length, as we didn’t adopt any pre-trained model for embeddings.
3.2.2. Input Vectors for the Transformer Encoder
After obtaining the embeddings, our model constructs the input vectors for the Transformer Encoder, consisting of two types of input: IEU (Input regarding End-of-Unit tests) and IIU (Input regarding In-Unit assignments). As we will introduce in the next section, IEU vectors will serve as the queries, while IIU vectors will serve as the keys and values.
To derive IEU vectors, we follow a series of steps. Firstly, we concatenate the problem embedding, problem features, sequence embedding, and the sum of five levels of sequence level embedding (levels 1 to 5). Specifically, problem features are the concatenation of numerical values, including problem type (dummy coded), problem text (BERT+PCA vectors), problem skill code (dummy coded), and indicators of whether the problem contains image/equation/video (booleans). We then pass them through a Multi-Layer Perceptron (MLP) to capture essential features. To further enrich the representation, we utilize skip connections to aggregate sequence embedding and sequence level embedding. Subsequently, we combine the output with student embedding and class embedding through element-wise addition to derive the final IEU vectors.
The construction of IIU vectors follows a similar process, with two notable differences. One is that after the skip connections, unlike IEU vectors, we put encoded action logs (concatenated action type embedding and action features) instead of student embedding into the mix. Adding the action information allows us to utilize important behavioral features from the dataset, while omitting student embedding enhances the generalizability of the model. The other difference is that we add a positional encoding layer before obtaining the final IIU vectors. This layer assigns unique position-specific values to each token’s embedding, facilitating the model’s understanding of the relative positions of tokens within the sequence. The inclusion of positional encoding empowers the model to leverage the sequential nature of the data better when making predictions. We employ the positional encoding as introduced in the original attention-based model paper (Vaswani et al., 2017):
\begin {align} PE_{(pos, 2i)} = \sin \left (\frac {pos}{10000^{2i/d_{model}}}\right ) \\ PE_{(pos, 2i+1)} = \cos \left (\frac {pos}{10000^{2i/d_{model}}}\right ) \end {align}
where \( pos \) represents the position, \( i \) denotes the dimension, and \( d_{model} \) is the dimension of the model.
As Figure 2 shows, a key distinction between the in-unit and end-of-unit problems in the model is the inclusion of action-related information in IIU vectors, but not in IEU vectors. This differentiation is aligned with our model’s focus on predicting only correct or incorrect responses for end-of-unit test problems. Furthermore, we incorporate student embeddings in the end-of-unit test problems to account for variations in exam outcomes across different student populations even when they have the same action sequences.
3.2.3. Multi-head Attention Mechanisms
The core component in the Transformer Encoder is the attention mechanism (Vaswani et al., 2017). Attention allows the model to assign different weights, or attention scores, to different elements of the input sequence. By assigning higher weights to more important elements and lower weights to less important ones, the model can effectively allocate its attention resources and capture the most relevant information.
Formally, denote by \(\mathcal {D} \stackrel {\mathrm {def}}{=} \{\textbf {K}, \textbf {V}\}\) a database of key matrix \(\textbf {K}\) and value matrix \(\textbf {V}\), and denote by \(\textbf {Q}\) a query matrix. Then the scaled dot-product attention over \(\mathcal {D}\) is defined as
\begin {equation} \text {Attention}(\textbf {Q}, \textbf {K}, \textbf {V}) = \text {softmax}_{\text {row}}(\frac {\textbf {Q}\textbf {K}^T}{\sqrt {d_k}})\textbf {V} \end {equation}
where the softmax function is applied for each row of its input.
In simple terms, a query (q) is like a question, the keys (k) are like the keywords of a set of possible answers, and a value (v) is the actual content or features of each answer. By comparing the query with the keys, the attention mechanism determines the relevance or importance of each key to the query. The resulting attention scores are then used to weigh the corresponding values.
We adopted single-head attention in our main model (Model 1). However, in our further attempts, we leveraged multi-head attention, a module for attention mechanisms that run through an attention mechanism several times in parallel. The independent attention outputs are then concatenated and linearly transformed into the expected dimension. Formally, we define
\begin {align} \text {MultiHead}\left (\textbf {Q}, \textbf {K}, \textbf {V}\right ) = \left [\text {head}_{1},\dots ,\text {head}_{h}\right ]\textbf {W}_{0} \\ \text {where} \text { head}_{i} = \text {Attention} \left (\textbf {Q}\textbf {W}_{i}^{Q}, \textbf {K}\textbf {W}_{i}^{K}, \textbf {V}\textbf {W}_{i}^{V} \right ) \end {align}
where \(\textbf {W}_{i}^{Q}, \textbf {W}_{i}^{K}\), and \(\textbf {W}_{i}^{V}\) are the weights matrices of head \(i\) for the queries, keys, and values respectively.
In our approach, we take the IEU vectors as the queries (\(\mathbf {Q}\)) and the IIU vectors as both the keys (\(\mathbf {K}\)) and values (\(\mathbf {V}\)) in the multi-head attention mechanism. The IEU vectors comprise information about the students whose scores we intend to predict, while the IIU vectors integrate additional data from action logs containing behavioral features. By doing so, the model can attend to specific aspects related to each token in both process data and curricula information when computing the attention scores. In addition, using the same keys and values simplifies the computations as they can be performed simultaneously.
For every student and problem ID in the query, the multi-head attention module assigns weights to the relevant problem and action log entries (values) based on their importance with respect to the student’s specific query. By doing so, the module generates predictions for the student’s performance on that particular problem. This process is repeated for each student and problem combination, enabling the model to make individualized predictions for all students and their respective problems based on their unique characteristics and interactions.
3.2.4. Output Layer
After getting the output of the attention layer, we feed it to a 1-layer MLP that ends with a sigmoid function. Hence, for each assigned unit test problem, the model outputs a value between 0 and 1, which corresponds to the estimated score of the student on the problem.
3.3. Alternative Choices of Architecture and Ensemble Modeling
We evaluated the performance of four slightly different model architectures based on the model architecture introduced in Section 3.2 to examine how changing some components in the model affects the prediction results and to evaluate ensemble modeling, a technique that combines the predictions of multiple individual models to obtain a more accurate and robust prediction. Table3 presents the comparison of all four slightly modified model architectures, including the original model. Compared to the first model (i.e., the model introduced in Section 3.2), the second model had a wider width of layers in the MLP used for problem embeddings. The number of heads of the Transformer Encoder was increased to 10. These modifications would increase the complexity of the model, which could lead to better accuracy and/or overfitting in the model. In addition, student and class embeddings were added together, processed together in the same MLP, and added to the IIU vectors and IEU vectors. The third model possessed the same architecture as the second model, but with more layers for the student and class MLP, and it only used the sequence level embeddings up to “sequence_folder_path_level_3,” which means that the sequence level embeddings would not contain very specific information to avoid overfitting the sequence level embeddings. The fourth model was similar to the third model except for the number of heads of the Transformer Encoder being two.
| Model 1 (base) | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|
| Layers Width in MLP for Problem Embeddings | 40 | 100 | 100 | 100 |
| Number of Layers for Student and Class MLP | 2 | 2 | 3 | 3 |
| Whether Student and Class Embeddings Added and Processed together | No | Yes | Yes | Yes |
| Sequence Levels Used for Generating Sequence Level Embeddings | 1-5 | 1-5 | 1-3 | 1-3 |
| Number of Heads in Transformer Encoder | 1 | 10 | 10 | 2 |
To further evaluate the possibility of improving the AUCs, we also implemented an ensemble modeling method that was ultimately used as a submission to the EDM Cup 2023. For ensemble modeling, we adopted rank averaging, a type of soft voting as per Sherazi et al. (2021), to aggregate the predictions from all four types of models. This is because the area under the receiver operating characteristic curve (AUC) was used as our evaluation metric, which is also computed based on ranks in nature. The goal of rank averaging was to combine the rank orders generated by individual models to create a final aggregated rank order. Note that as a submission to the EDM Cup 2023, we further included another distinctively trained Model 4 in our ensemble model because it led to the highest average validation and we thought it had the potential to be the best model, thus aggregating five trained models in total.
Suppose we have a set of \(k\) individual models, denoted as \(M_1, M_2, \cdots , M_k\), and the predictions made by model \(M_i\) for instance \(j\) is \(P_{ij}\) (\(j = 1, \cdots , n\)). Then the average rank of the \(j^{th}\) instance is
\begin {align} \bar {R}_{j} &= \frac {\sum _{i=1}^{k}{\operatorname {rank}(P_{ij})}}{k} \end {align}
where \(\operatorname {rank}(P_{ij})\) is the ascending rank of \(P_{ij}\) among \(P_{i1}, \cdots , P_{in}\).
Next, we normalize \(\bar {R}_{j}\) with the min-max method such that it falls within \((0, 1)\). Therefore, the final aggregated score of the \(j^{th}\) instance over the \(k\) models is
\begin {align} Score_{j} &= \frac {\bar {R}_{j} - \min \{\bar {R}_{1}, \cdots , \bar {R}_{n}\}}{\max \{\bar {R}_{1}, \cdots , \bar {R}_{n}\} - \min \{\bar {R}_{1}, \cdots , \bar {R}_{n}\}} \end {align}
3.4. Evaluation Methodology
The dataset was divided by EDM Cup 2023 organizers into 75% for training and 25%
for evaluation. More specifically, StratifiedGroupKFold by scikit-learn(Pedregosa
et al., 2011) was used to stratify the dataset by sequence ID and grouped by teacher ID
so that no teacher had data in both the training and evaluation datasets, and the number of assignments
from each sequence was also split into approximately 3:1 in training and evaluation respectively. At the
time of the Kaggle competition, the true scores in the evaluation dataset were completely hidden, and
we could only submit predictions to the website to see the AUC scores. The evaluation dataset
was further split into halves: public half and private half evaluation datasets. The public
evaluation dataset gave feedback (i.e., AUC scores of submitted predictions) to the competition
participants, and the private evaluation dataset was used for the final evaluation of models. Thus,
overfitting the public evaluation dataset might have caused a worse result for the private AUC
score.
In training, we employed 10-fold cross-validation to evaluate and select the best predictive model.
The procedure involved dividing our dataset into ten almost equally sized folds. Here, we used KFold
by scikit-learn to generate 10 folds by treating each student as a data point. This
was because our model took all the assignments completed by a single student as input
for prediction. Thus, if one student was included in one fold, their assignment data would
never be included in another fold. During each iteration, we utilized nine folds to train the
models, while the remaining fold served as an independent validation dataset. This process
was repeated ten times to ensure that each fold was utilized as a validation dataset exactly
once.
To measure the performance of our models, we employed AUC as the evaluation metric. For each iteration of the cross-validation process, we computed the AUC value for the model using the corresponding validation dataset. Subsequently, we selected the model with the highest AUC value among the models estimated for each fold. To obtain a comprehensive measure of model performance, we also calculated the average AUC by computing the mean of the AUC values derived from all ten iterations. This average AUC provided a robust estimation of the predictive capability of our models across different validation datasets.
4. Results
4.1. Model Performance
| Best Validation | Average Validation (SD) | Evaluation (Public) | Evaluation (Private) | |
|---|---|---|---|---|
| Model 1 | 0.8156 | 0.8035 (0.0051) | 0.78897 | 0.79083 |
| Model 2 | 0.8132 | 0.8067 (0.0034) | 0.78725 | 0.78617 |
| Model 3 | 0.8117 | 0.8066 (0.0029) | 0.78805 | 0.78458 |
| Model 4 | 0.8150 | 0.8070 (0.0038) | 0.78769 | 0.78427 |
| Ensemble | N/A | N/A | 0.79038 | 0.78969 |
Table 4 presents the summary of the AUC calculated from the 10-fold cross-validation and the evaluation datasets. It is worth noting that Model 1 has the highest best validation, private evaluation, and the second-best public AUC while having the lowest average validation AUC. Therefore, as a learned model without ensembling, Model 1 is the best model. It is notable that Model 1 outperforms Model 2 despite the latter’s greater complexity, including a broader layer width in its MLP for problem embeddings and additional heads in the Transformer Encoder. This discrepancy may suggest that Model 2 is overfitting the data. The ensemble model gives the best public evaluation AUC and also the second-best private evaluation AUC although the majority of the models (Models 2, 3, and 4) within the ensemble model perform worse than the ensemble model itself, which could suggest that the ensemble modeling stabilizes and improves prediction results. However, note that the ensemble model does not perform better than Model 1, suggesting that we can just use Model 1 in practice.
4.2. Ablation Study
Given the complexity of our dataset and model, assessing the impact of each model component is crucial. We selected Model 1, as it consistently outperformed others in evaluation metrics. Our ablation study involved omitting specific inputs and their corresponding model components, allowing us to observe changes in AUC scores.
| Model 1 | Best Validation | Average Validation (SD) | Evaluation (Public) | Evaluation (Private) |
|---|---|---|---|---|
| Original | 0.8156 | 0.8035 (0.0051) | 0.7890 | 0.7908 |
| Without Sequence Level Embeddings | 0.8088 | 0.8052 (0.0027) | 0.7854 | 0.7865 |
| Without Student/Class Embeddings | 0.8108 | 0.8057 (0.0041) | 0.7877 | 0.7842 |
| Without Action Features | 0.8108 | 0.8048 (0.0029) | 0.7856 | 0.7835 |
| Without Action Features and Student/Class Embeddings | 0.8110 | 0.8029 (0.0040) | 0.7826 | 0.7826 |
| Without Problem Features | 0.8084 | 0.8052 (0.0024) | 0.7870 | 0.7816 |
| Without All Features Above | 0.8088 | 0.8041 (0.0034) | 0.7851 | 0.7802 |
Table 5 presents the results of the ablation study. The models are sorted in descending order by the AUC for the private evaluation dataset. We specifically evaluated Model 1 without action features and without student and class embeddings, as these configurations do not rely on user-specific information and thus facilitate interpretation. Note that “Without All Above Features” implies Model 1 solely relies on action type, sequence, and problem embeddings.
Generally, the original Model 1 has the largest best validation, public and private evaluation AUCs, suggesting that removing any component from Model 1 leads to a decrease in AUC scores. Note that the average validation score of the original Model 1 is the lowest, suggesting that the variability of the cross validation AUC for each fold is high, as demonstrated by the SD, possibly because of the complexity of the model. Table 5 also shows that removing all the additional features in the table will result in both the lowest public and private evaluation AUCs, suggesting the importance of incorporating all the additional features to maximize the performance of the model. When examining each component individually, the AUC reduction appears small, as they only perform better at either public or private dataset. From these results, a certain type of additional features might only improve predictions for a small subset of the dataset. However, using all the additional features will help the model perform better at both the public and private evaluation datasets.
4.3. Interpretation
We use Model 1 for interpretation because it performs as well as the ensemble model, and it is simpler than others since it only uses one head in the Transformer Encoder.
We first begin by understanding the importance of each action type. We use the attention weights from the Transformer Encoder to estimate the importance of each action type. The utilization of attention weights to interpret a deep learning model which relies on the attention mechanism is very common (Pandey and Karypis, 2019, Yeh et al., 2023). We propose two kinds of importance measures: the importance of action (IA) and the importance of a single action (ISA). First, we define a function for a single-head Transformer Encoder, \(\text {attnW}(\mathbf {q}, \mathbf {K})\), to calculate attention weights. Given a query row-vector \(\mathbf {q}\) and a key matrix \(\mathbf {K}\), the function is defined as:
\begin {align} \text {attnW}(\mathbf {q}, \mathbf {K}) = \text {softmax}(\frac {\mathbf {q W}^Q(\mathbf {K} \mathbf {W}^K)^T}{\sqrt {d_k}}). \end {align}
where \(\mathbf {W}^Q\) and \(\mathbf {W}^K\) are weight matrices for queries and keys, respectively, and \(d_k\) is the dimensionality of the key vectors.
The importance of an action type \(v\), denoted as \(IA_v\), is calculated by averaging the attention weights associated with that action type across all queries and students. The formula is:
\begin {align} IA_v = \frac {1}{N}\sum _{i}^{N} \frac {1}{n_i^Q} \sum _{\mathbf {q} \in \mathbf {Q}_i} \sum _{j = 1}^{n_i^K} \text {I}(A_{ij} = v) [\text {attnW}(\mathbf {q}, \mathbf {K}_i)]_j \end {align}
where \(N\) is the number of students, \(\mathbf {Q}_i\) is the query matrix for student \(i\), \(n_i^Q\) is the number of queries for student \(i\), \(\mathbf {K}_i\) is the key matrix for student \(i\), \(n_i^K\) is the number of keys for student \(i\), and \(\mathbf {A} = (A{ij})\) is a matrix indicating action types, with \(A{ij}\) representing the action type of the \(j\)-th action of student \(i\).
To illustrate the computation of \(\sum _{j=1}^{n_i^K} \text {I}(A_{ij} = v) [\text {attnW}(\mathbf {q}, \mathbf {K}i)]j\) within the formula, consider this example: \(\text {attnW}(\mathbf {q}, \mathbf {K}_i) = [0.1, 0.1, 0.2, 0.2, 0.4]\) and \(\mathbf {A}_{i*} = [1, 2, 2, 3, 2]\), representing the attention weights and action types for student \(i\), respectively. For action type \(v = 2\), the sum \(\sum _{j} \text {I}(A_{ij} = v) [\text {attnW}(\mathbf {q}, \mathbf {K}_i)]_j\) is calculated as \(0.1 + 0.2 + 0.4 = 0.7\), which is the sum of the attention weights corresponding to action type \(v\) (indices 2, 3, and 5). Finally, \(IA_v\) is an average of these sums over all queries and students, providing a measure of the importance of each action type.
IA calculates how much the predictions could be explained by a specific action type. It ranges between \(0\) and \(1\), and sums up to \(1\) across action types. Therefore, IA is affected by the distribution of actions, which makes \(IA_j\) higher when action \(j\) is taken more frequently than others. For example, if IA for correct response in the action log is 40%, 40% of attention weights are given to correct responses in the action log.
On the other hand, the importance of a single action takes into account the frequency of actions taken by students, and explains the impact of taking a single action. Let us denote that \(n_{iv}^K = \sum _k I(A_{ik} = v)\), which is the count of actions associated with action type \(v\) taken by student \(i\).
\begin {align} ISA_v = \frac {1}{\sum _{i} I(n_{iv}^K > 0)}\sum _{i}^{N} I(n_{iv}^K > 0) \cdot \frac {1}{n_i^Q} \cdot \frac {n_i^K}{ n_{iv}^K } \sum _{\mathbf {q} \in \mathbf {Q}_i} \sum _{j = 1}^{n_i^K} \text {I}(A_{ij} = v) [\text {attnW}(\mathbf {q}, \mathbf {K}_i)]_j. \end {align}
Here, \(I(n_{iv}^K > 0)\) is an indicator function that checks whether student \(i\) has performed any action of type \(v\). The denominator, \(\sum _{i} I(n_{iv}^K > 0)\), counts the number of students who have performed at least one action of type \(v\), normalizing the value across students.
To illustrate this with a previous example, consider \(\frac {n_i^K}{n_{iv}^K } \sum _{\mathbf {q} \in \mathbf {Q}i} \sum _j \text {I}(A_{ij} = v) [\text {attnW}(\mathbf {q}, \mathbf {K}_i)]j\). Since \(n_i^K = 5\) and \(n_{iv}^K = 3\), the calculation becomes \(\frac {5}{3}(0.1 + 0.2 + 0.4) \simeq 1.17\). This sum is normalized because three of the five actions correspond to action type \(v = 2\). ISA then represents the average of these normalized values across all queries and students who have performed at least one action of type \(v\).
The ISA value provides a comparative measure of the relative impact of a single instance of a specific action type. It averages the normalized attention weights for each action type for a student, where these weights are expected to sum to 1 (due to the softmax function in the attention weight calculation). This average is then taken across all students who have taken at least one action of type \(v\). An ISA value below 1 implies that the action type has a lesser relative importance compared to other actions, whereas a value above 1 indicates a higher relative importance.
| Action | Count | Proportion | IA | ISA |
|---|---|---|---|---|
| Assignment started | 686,862 | 0.080 | 0.120 | 1.0305 |
| Correct response | 3,826,150 | 0.443 | 0.409 | 0.9456 |
| Wrong response | 1,692,483 | 0.196 | 0.196 | 1.0601 |
| Open response | 1,681,964 | 0.195 | 0.186 | 0.9933 |
| Answer requested | 640,317 | 0.074 | 0.078 | 1.1293 |
| Hint requested | 82,187 | 0.010 | 0.008 | 1.0303 |
| Explanation requested | 23,380 | 0.003 | 0.003 | 1.0983 |
| Skill related video requested | 1,341 | 0.000 | 0.000 | 1.1122 |
| Live tutor requested | 176 | 0.000 | 0.000 | 0.9666 |
Table 6 shows the IA and ISA for the action types associated with problems that were used for prediction in our model, along with the counts and proportions of actions by students who have completed end-of-unit test assignments. Based on the IA values, “wrong response,” “correct response,” and “open response” are the types of actions that are most predictive. This could be due to the differences in the frequency of action instances for each type. IA for all the action types have similar values as the proportions of action type counts. Therefore, “wrong response,” “correct response,” and “open response” are the most influential action types because they tend to appear most frequently.
On the other hand, the effect of a single instance of an action type is different among all the action types, which explains why the IA values from Table 6 and the proportions of action type counts do not exactly match. When we look at ISA, “correct response” and “open response” have lower values (smaller than 1), meaning that a single action of either type has lower influences on predictions. This is because both types of responses could be made easily after certain types of action types such as “answer requested” and “explanation requested,” and these action types might be more informative when predicting students’ ability and scores. In fact, the ISA of “answer requested” and “explanation requested” are 1.1293 and 1.0983 respectively, and higher than both “correct response” and “open response.” Note that “skill related video requested” also has a high ISA value, but we refrained from making generalizations due to its limited sample size. Thus, single instances of “correct response” and “open response” have the least information when predicting students’ scores.
4.4. Effects of Actions
4.4.1. Main effects
To demonstrate the effects of actions on the end-of-unit test problems, we construct artificial action logs constituting the top 100 popular in-unit problems with only a certain type of action to estimate the average probabilities of getting a correct answer. Specifically, we focus on a subset of the total 14 types of actions that are associated with problems: three types of responses (correct, wrong, and open) and five types of requests (answer, hint, explanation, skill-related video, and live tutor). Note that we used Model 1 without action features and student/class embeddings, which was introduced in Section 4.2, Ablation Study, for ease of constructing the artificial action logs. In addition, since every student begins with “assignment started,” we inserted an “assignment started” action at the beginning, setting the same sequence ID as the most popular problem. Then, we predict the probabilities of getting correct responses for the top 100 popular end-of-unit test assignment problems. By calculating the average probability of getting correct responses, we can evaluate how taking a certain action affects predictions. We call these effects “main effects” because we do not consider any interactions with any other action type for each action.
Figure 3 shows the average probabilities of getting correct responses for the end-of-unit test problems, given that all the actions for the in-unit assignment problems are of the same type. As expected, “correct response” gives the highest average probability for correct responses. Also, “open response” gives the second-highest average probability, meaning that doing open response problems leads to higher scores. Conversely, the action type “answer requested” results in the lowest average probability, even lower than that of “wrong response.” This may be due to factors such as students’ reduced motivation or lack of proficiency, which leads them to request answers instead of attempting to solve problems. Another potential explanation is the difference in the abilities of the student populations who do and do not make such requests. That is, students who request answers might have a lower average ability level than those who do not. Consequently, it’s challenging to definitively conclude why the probabilities associated with ”answer requested” are even lower than those for ”wrong response.” Similarly, for actions like ”explanation requested,” and ”hint requested,” we observe a trend of lower average probabilities than that of “wrong response.”
It is worth noting that “live tutor requested” gives a very high average probability; however, it is difficult to generalize this result because the sample size for “live tutor requested” is very limited. According to Table 6, “live tutor requested” has the least number of instances and thus the result could be attributed to the very limited sample rather than the effect of the action itself. For a similar reason, “skill related video requested” gives a slightly higher probability than “wrong response.” Given this limitation, we refrain from concluding the effect of the ”live tutor requested” and “skill related video requested” actions within the scope of this study.
4.4.2. Joint Effects
We observed that action types such as ”answer requested,” ”hint requested,” or ”explanation requested” typically indicate lower probabilities of correct responses, and we theorized that it could be attributed to the lower ability levels of the students who tend to request these forms of assistance. To further investigate this, we examine a situation where these requests are made following each incorrect response. This is to assess whether such requests could potentially lead to an improvement in scores. For this investigation, we utilize the same artificial dataset as in the previous section, but with a modification: we inserted a ”wrong response” before each instance of these help requests. This approach allows us to more accurately evaluate the impact of these help-seeking actions on student performance, especially in the context of their response to wrong answers.
The joint effects of a “wrong response” and a request suggest similar patterns as the main effects of the request itself (Figure 3). Notably, when a ”wrong response” precedes a request for assistance, it generally leads to a higher probability of a correct response compared to situations where no ”wrong response” is involved. This indicates that students are more likely to answer correctly if they initially attempt in-unit assignment problems and subsequently seek assistance, rather than avoiding attempting the problems before seeking assistance. This may be attributed to the enhanced learning effects when students actively engage with problems before seeking help. However, since this study does not involve any experimental design, further research is necessary to explore the causal link between these observations by possibly experimenting.
Finally, these artificial action logs do not take into account that “correct response” might follow these requesting actions by knowing how to solve problems after a request action. We also simulate such cases by including “correct response” after each requesting action. As shown in Figure 3, the triple joint effects of “wrong response”, a request, and “correct response” are all higher than the double joint effects, and higher than a single requesting action. This outcome is expected as it reflects scenarios where students correctly answer questions after receiving assistance, indicating a more effective learning process compared to the other two scenarios. Note that because “correct response” typically receives the smallest attention weight, the request action types will be more important when predicting students’ scores.
4.5. Inferring the Effects of Input Vectors from Data
In addition, we also extracted the effects of actions from the input (IIU) vectors for the Transformer Encoder. Because IIU vectors are used for both Key and Value for the Transformer Encoder, the information contained in IIU vectors is directly related to both attention weights and predicted probabilities of correct answers. Therefore, if we could interpret IIU vectors, we would be able to understand how action types will influence the prediction results. We did not analyze IEU vectors because it is used as the query (\(\mathbf {Q}\)) and does not contain much useful information. In this section, we used the same model as the previous section (Model 1 without action features and student/class embeddings).
More specifically, we took the following steps. First, we saved all the IIU vectors generated while predicting end-of-unit test problems. The IIU vectors are transformed by the weight matrix, \(\mathbf {W}^K\), of the head of the transformer. Contrary to Section 4.3, we used the real action logs for analysis. Second, since action types are very imbalanced, we randomly under-sampled input vectors in majority classes and over-sampled input vectors in minority classes using SMOTE (Chawla et al., 2002). Because it has a moderately large sample size, we used “answer requested” as the reference class for both over-sampling and under-sampling so that all other classes have the same count as “answer requested,” \(686862\).
Third, we applied Neighborhood Components Analysis (Goldberger et al., 2004) to find a linear transformation of IIU vectors that predicts action types the best, which we call NCA scores. We believe NCA gives us insights into the input vectors because NCA finds a linear transformation of the input space such that the k-nearest neighbor performs well in the transformed space (Goldberger et al., 2004). This implies that action types yielding similar NCA scores are likely to be similar. Since the input vectors are used to compute attention weights and predicted probabilities, this similarity in action types is indicative of similar predicted probabilities. Finally, since the scale is not identifiable, we standardized the NCA scores and calculated their means and standard deviations for each action type. We interpret how types of actions are similar to each other in terms of their effects on predicted probabilities.
| Action | Mean | SD |
|---|---|---|
| correct response | 1.65 | 0.08 |
| open response | 1.27 | 0.10 |
| live tutor requested | 0.80 | 0.09 |
| skill related video requested | 0.42 | 0.07 |
| wrong response | -0.36 | 0.08 |
| hint requested | -0.71 | 0.06 |
| explanation requested | -0.87 | 0.07 |
| answer requested | -1.10 | 0.10 |
Table 7 presents the summary of mean and standard deviations for NCA scores across different action types. The order of action types by NCA scores aligns with the order of average probability correctness for the main effects, as shown in Figure 3. This alignment is further substantiated by a perfect Spearman’s rank correlation (\(\rho = 1\)), indicating a direct correspondence between the two orders. Furthermore, the standard deviations are small across action types, reinforcing the reliability of these insights. Therefore, the results demonstrate that we can infer the main effects of action types just from the data without using the artificial action logs procedure.
5. Problem Associations
Analyzing problem associations is a popular application of knowledge tracing models (Piech et al., 2015, Pandey and Karypis, 2019). In this section, we demonstrate it using our model following a similar procedure to SAKT, which is based on attention weights (Pandey and Karypis, 2019). In our context, it could be especially useful since some in-unit assignment problems are more predictive than others. If we can identify in-unit assignment problems that are very predictive of their end-of-unit test scores, teachers might be recommended to include these problems in an assignment before end-of-unit tests and make sure students can solve these problems, as we have demonstrated that having a correct response after a wrong response improves their score.
Associations between in-unit and end-of-unit test problems could be inferred from attention weights computed by the Transformer Encoder. By taking the same procedure as Section 4.3.1, we constructed artificial action logs constituting correct responses to the 20 most popular in-unit assignment problems. Note that for this analysis, we used the original Model 1 because using the auxiliary information, especially problem and sequence features, improved learning the problem associations better. In generating the artificial action logs, for action features, we used no tutoring option, a single attempt, no time spent, and mean values for the timestamp, time, and day. We used zero vectors for the student embedding. Then, we predicted the 20 most popular end-of-unit test problems and obtained attention weights generated by the model.
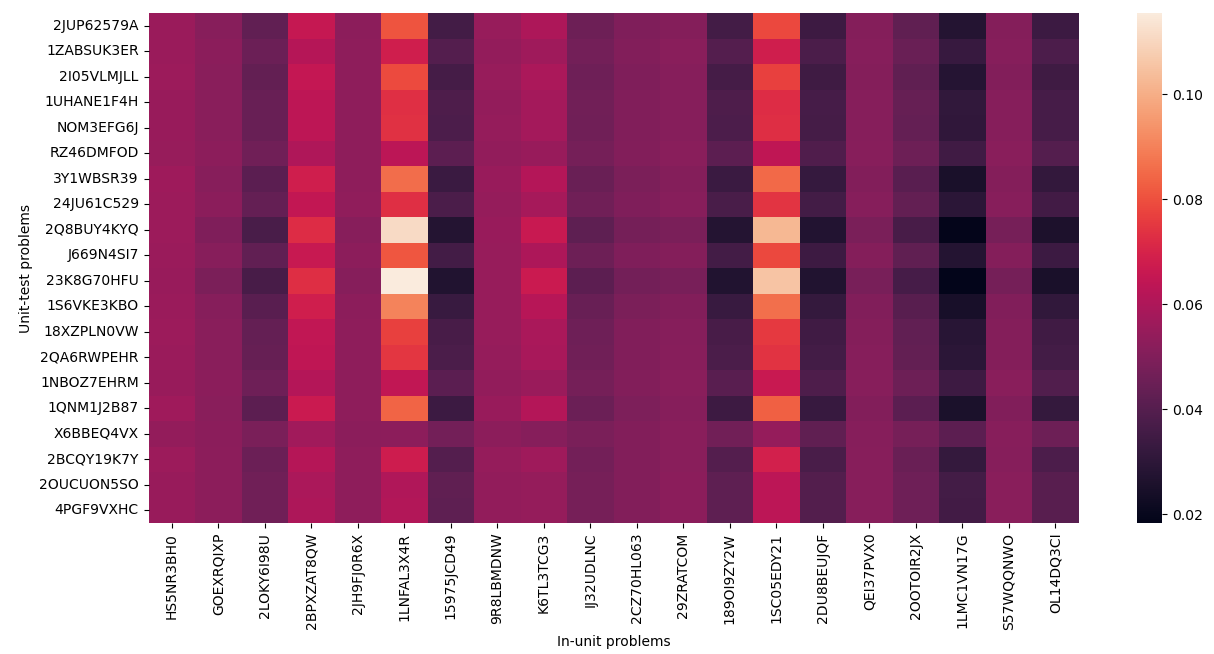
Figure 4 shows the attention weights for the 20 most popular in-unit and end-of-unit test problems. We can observe that some in-unit assignment problems are more predictive than others. For example, problem 1LNFAL3X4R consistently yields higher attention weights than 189OI9ZY2W. Therefore, having a score of 1LNFAL3X4R is much more informative than 189OI9ZY2W. On the other hand, some end-of-unit test problems are more “picky” than others in terms of their associations with in-unit assignment problems. For example, attention weights for 23K8G70HFU have more variance: very high for 1LNFAL3X4R and very low for 189OI9ZY2W, while those for X6BBEQ4VX have less variance: similar weights between 1LNFAL3X4R and 189OI9ZY2W. Therefore, we can assume that some end-of-unit tests might rely on very specific skills, leading to depend on certain in-unit assignment problems (i.e., “tricky” about skills and problems).
5.1. Visualizing Problem Associations
The importance of designing instruction based on knowledge components is a key focus among researchers (Koedinger et al., 2012, diSessa, 1993). Within the Knowledge Learning Instruction (KLI) framework, a knowledge component is defined as “an acquired unit of cognitive function or structure that can be inferred from performance on a set of related tasks” (Koedinger et al., 2012). Knowledge components exhibit variations in complexity, domain, applicability (whether constant or variable), and responses (constant or variable). Although our dataset already labels knowledge components at the problem level using ’The Common Core State Standards for Mathematics skill code,’ and at the sequence level by grade or subject information from the Kendall Hunt Illustrative Mathematics curriculum or the Engage New York mathematics curriculum, it remains valuable to demonstrate the ability to identify potential knowledge components directly from data. For instance, Pandey and Karypis (2019) demonstrated the discovery of problem relevance through problem association from attention weights, leading to the creation of a graph that represents latent concepts, which are likely correlated with knowledge components.
Although technically feasible, replicating this method is difficult in our model, particularly in accurately predicting attention weights for the same set of problems. This difficulty arises because, in our dataset, a problem is categorized exclusively as either in-unit or end-of-unit, not both. Consequently, during the training process, queries are assigned solely to end-of-unit problems, while key and value pairs are restricted to in-unit problems. This distinction complicates the application of the method in our context because the problem associations between in-unit problems are not explicitly learned. Additionally, the sparsity of our dataset presents another obstacle in predicting knowledge components. With a total of 132,738 problems, it becomes difficult to identify global knowledge components that comprehensively explain various topics because users only solve a very small subset of the problems.
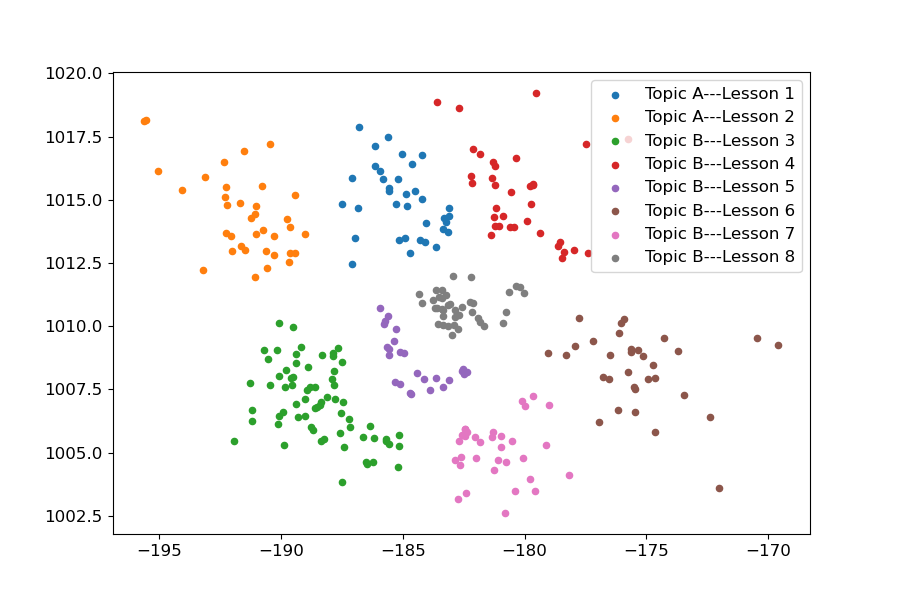
Therefore, we propose a simpler procedure to demonstrate the capability of our model to learn knowledge components. This involves employing the same NCA (Neighborhood Component Analysis) procedure outlined in Section 4.5. In this process, we use the IIU vectors as input for the NCA, resulting in a two-dimensional output vector based on the lowest sequence level information. The IIU vectors are derived from each problem within a specific sequence, in this example, ’EngageNY/Eureka Math, Grade 2, Module 1 - Sums and Differences to 100 (OA, NBT).’ As depicted in Figure 5, this approach yields a two-dimensional plot where IIU vectors are separated by topics. The topics are well separated in the plot, and some problems within a single topic are more clustered than others, which suggests a smaller knowledge component within the topic. For instance, within Topic B, Lesson 5, we observe distinct sub-clusters within the main topic cluster. This finding suggests the potential for further identifying smaller knowledge components.
6. Discussion and Conclusion
In this study, we proposed a novel framework for the ASSISTments dataset, comprising detailed preprocessing and a Transformer-based predictive model. Our approach primarily utilizes the action log from the ASSISTments server to forecast future learning outcomes. To boost prediction accuracy, the model incorporates extensive data on problem details and sequences. A key feature of our Transformer-based model is its ability to process in-unit and end-of-unit test problems differently by constructing separate inputs from their respective auxiliary features such as action features and student embeddings. Remarkably, our model secured the top position on the leaderboard at the EDM Cup 2023 using a private dataset, demonstrating superior prediction accuracy and generalizability compared to other entrants. Despite the complexity of our model, we introduced interpretation methods to understand the impact of different action types on end-of-unit test scores. We have detailed the influence of each action type in the action log and explored problem-problem associations to gauge how in-unit assignment problems might affect specific end-of-unit test problems. This investigation has also led to the identification of problem clusters based on their topics.
Our study contributes significantly to methodological developments in modeling and interpretation, yet we recognize several limitations. First, due to the complex network architecture of our model, it is challenging to interpret it without applying some modifications. Especially if one wants to use artificial action logs for interpretation, they must either simulate student embeddings and action features like timestamps or omit these inputs and components as we did in our study. While simulating student embeddings is feasible using zero vectors, accurately faking timestamps is more challenging because the timestamp is a variable that is affected by many factors such as students’ ability, personality, and learning materials. Therefore, future research should consider designing a model architecture that uses both of these types of information without sacrificing interpretability. Second, we did not conduct a direct quantitative performance comparison with existing methods such as SAKT (Pandey and Karypis, 2019) and SAINT (Choi et al., 2020) as well as others in the EDM Cup 2023 due to limited time and resources and/or model availability. Future studies should include comprehensive evaluations of other models featured in this special issue. Third, the class imbalance of action types poses a challenge, particularly in drawing conclusions for certain action types with small sample sizes, such as “skill-related video requested” and “live tutor requested,” which have only 1,341 and 176 actions, respectively. This necessitates further evaluation with larger sample sizes. Fourth, our model has limited capability in learning associations among in-unit problems, especially at a larger scale. This is because of the nature of the task, focused as it is on predicting end-of-unit problem responses from in-unit problems. Contrarily, traditional knowledge tracing models, which predict responses within an action log, tend to learn these associations more effectively. To improve this aspect, future work could explore methods like self-supervised learning (Balestriero et al., 2023) to better capture these in-unit problem associations.
7. Acknowledgments
We thank the organizers of the EDM Cup 2023 for allowing us to access the new ASSISTments dataset.
8. Competing interests
The authors declare no competing interests.
9. Declaration of Generative AI Software Tools in the Writing Process
During the preparation and revision of this work, the author(s) used ChatGPT in all sections for polishing. After using this tool, the author(s) reviewed and edited the content as needed and takes full responsibility for the content of the publication.
References
- Abdelrahman, G., Wang, Q., and Nunes, B. 2023. Knowledge tracing: A survey. ACM Computing Surveys 55, 11.
- Baker, R. S. J. d., Corbett, A. T., and Aleven, V. 2008. More accurate student modeling through contextual estimation of slip and guess probabilities in bayesian knowledge tracing. In Intelligent Tutoring Systems, B. P. Woolf, E. Aïmeur, R. Nkambou, and S. Lajoie, Eds. Springer Berlin Heidelberg, Berlin, Heidelberg, 406–415.
- Balestriero, R., Ibrahim, M., Sobal, V., Morcos, A., Shekhar, S., Goldstein, T., Bordes, F., Bardes, A., Mialon, G., Tian, Y., Schwarzschild, A., Wilson, A. G., Geiping, J., Garrido, Q., Fernandez, P., Bar, A., Pirsiavash, H., LeCun, Y., and Goldblum, M. 2023. A Cookbook of Self-Supervised Learning. arXiv:2304.12210 [cs].
- Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer, W. P. 2002. SMOTE: Synthetic Minority Over-sampling Technique. Journal of Artificial Intelligence Research 16, 321–357.
- Choi, Y., Lee, Y., Cho, J., Baek, J., Kim, B., Cha, Y., Shin, D., Bae, C., and Heo, J. 2020. Towards an appropriate query, key, and value computation for knowledge tracing. In Proceedings of the Seventh ACM Conference on Learning @ Scale. L@S ’20. Association for Computing Machinery, New York, NY, USA, 341–344.
- Corbett, A. T. and Anderson, J. R. 1994. Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction 4, 253–278.
- diSessa, A. A. 1993. Toward an Epistemology of Physics. Cognition and Instruction 10, 2/3, 105–225. Publisher: Taylor & Francis, Ltd.
- Goldberger, J., Hinton, G. E., Roweis, S., and Salakhutdinov, R. R. 2004. Neighbourhood components analysis. In Advances in Neural Information Processing Systems, L. Saul, Y. Weiss, and L. Bottou, Eds. Vol. 17. MIT Press, 513–520.
- Heffernan, N. T. and Heffernan, C. L. 2014. The assistments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education 24, 470–497.
- Hochreiter, S. and Schmidhuber, J. 1997. Long short-term memory. Neural Computation 9, 8, 1735–1780.
- Koedinger, K. R., Corbett, A. T., and Perfetti, C. 2012. The Knowledge-Learning-Instruction Framework: Bridging the Science-Practice Chasm to Enhance Robust Student Learning. Cognitive Science 36, 5, 757–798.
- Kőrösi, G. and Farkas, R. 2020. MOOC Performance Prediction by Deep Learning from Raw Clickstream Data. In Advances in Computing and Data Sciences, M. Singh, P. K. Gupta, V. Tyagi, J. Flusser, T. Ören, and G. Valentino, Eds. Communications in Computer and Information Science. Springer, Singapore, 474–485.
- Li, X., Xiong, H., Li, X., Wu, X., Zhang, X., Liu, J., Bian, J., and Dou, D. 2022. Interpretable deep learning: Interpretation, interpretability, trustworthiness, and beyond. Knowledge and Information Systems 64, 12, 3197–3234.
- Liu, Q., Huang, Z., Yin, Y., Chen, E., Xiong, H., Su, Y., and Hu, G. 2019. Ekt: Exercise-aware knowledge tracing for student performance prediction. IEEE Transactions on Knowledge and Data Engineering 33, 1, 100–115.
- Lu, Y., Ober, T. M., Liu, C., and Cheng, Y. 2022. Application of Neighborhood Components Analysis to Process and Survey Data to Predict Student Learning of Statistics. In 2022 IEEE International Conference on Advanced Learning Technologies (ICALT). IEEE, 147–151.
- Lu, Y., Wang, D., Meng, Q., and Chen, P. 2020. Towards interpretable deep learning models for knowledge tracing. In Artificial Intelligence in Education, I. I. Bittencourt, M. Cukurova, K. Muldner, R. Luckin, and E. Millán, Eds. Springer International Publishing, Cham, 185–190.
- Medsker, L. R. and Jain, L. 2001. Recurrent neural networks. Design and Applications 5, 64–67.
- Moreno-Marcos, P. M., Pong, T.-C., Muñoz-Merino, P. J., and Delgado Kloos, C. 2020. Analysis of the Factors Influencing Learners’ Performance Prediction With Learning Analytics. IEEE Access 8, 5264–5282.
- Namoun, A. and Alshanqiti, A. 2021. Predicting Student Performance Using Data Mining and Learning Analytics Techniques: A Systematic Literature Review. Applied Sciences 11, 1, 237.
- Pandey, S. and Karypis, G. 2019. A self-attentive model for knowledge tracing. In Proceedings of the 12th International Conference on Educational Data Mining, C. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. EDM 2019 - Proceedings of the 12th International Conference on Educational Data Mining. International Educational Data Mining Society, 384–389.
- Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J., and Chintala, S. 2019. Pytorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems, H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, and R. Garnett, Eds. Vol. 32. Curran Associates, Inc., 8026–8037.
- Pavlik, P. I., Cen, H., and Koedinger, K. R. 2009. Performance factors analysis –a new alternative to knowledge tracing. In Proceedings of the 2009 Conference on Artificial Intelligence in Education: Building Learning Systems That Care: From Knowledge Representation to Affective Modelling. IOS Press, NLD, 531–538.
- Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E. 2011. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research 12, 2825–2830.
- Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L. J., and Sohl-Dickstein, J. 2015. Deep knowledge tracing. In Advances in Neural Information Processing Systems, C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett, Eds. Vol. 28. Curran Associates, Inc., 505–513.
- Sein Minn. 2022. AI-assisted knowledge assessment techniques for adaptive learning environments. Computers and Education: Artificial Intelligence 3, 100050.
- Sherazi, S. W. A., Bae, J.-W., and Lee, J. Y. 2021. A soft voting ensemble classifier for early prediction and diagnosis of occurrences of major adverse cardiovascular events for stemi and nstemi during 2-year follow-up in patients with acute coronary syndrome. PLOS ONE 16, 6 (06), 1–20.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L. u., and Polosukhin, I. 2017. Attention is all you need. In Advances in Neural Information Processing Systems, I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, Eds. Vol. 30. Curran Associates, Inc., 5998–6008.
- Wright, R. E. 1995. Logistic regression. In Reading and understanding multivariate statistics. American Psychological Association, Washington, DC, US, 217–244.
- Yeh, C., Chen, Y., Wu, A., Chen, C., Viégas, F., and Wattenberg, M. 2023. AttentionViz: A Global View of Transformer Attention. IEEE Transactions on Visualization and Computer Graphics, 1–11.
A. Action Types
Items marked with an asterisk are included in our model.
problem_started: The student started a problem.problem_finished: The student finished a problem.continue_selected: The student pressed the continue button after they finished a problem, moving them to the next problem in their assignment.correct_response*: The student submitted a correct response to a problem.wrong_response*: The student submitted an incorrect response to a problem.open_response*: The student submitted a response to an open-response question.assignment_started*: The student started their assignment.answer_requested*: The student requested the answer to a problem.assignment_finished: The student completed their assignment.assignment_resumed: The student resumed their assignment.hint_requested*: The student requested one hint from a set of hints for the problem.explanation_requested*: The student requested an explanation for the problemskill_related_video_requested*: The student requested a video that provides general instruction for the skill most related to solving the problem.live_tutor_requested*: The student requested a chat session with a live tutor.