Abstract
The prediction of student performance and the analysis of students’ learning behaviour play an important role in enhancing online courses. By analysing a massive amount of clickstream data that captures student behaviour, educators can gain valuable insights into the factors that influence students’ academic outcomes and identify areas of improvement in courses. In this study, we developed ClickTree, a tree-based methodology, to predict student performance in mathematical problems in end-unit assignments based on students’ clickstream data. Utilising extensive clickstream data, we extracted a novel set of features at three levels, including problem-level, assignment-level and student-level, and we trained a CatBoost tree to predict whether a student will successfully answer a problem in an end-unit assignment or not. The developed method achieved an Area under the ROC Curve (AUC) of approximately 79% in the Educational Data Mining Cup 2023 and ranked second in the competition. Our results indicate that students who performed well in end-unit assignment problems engaged more with in-unit assignments and answered more problems correctly, while those who struggled had higher tutoring request rates. We also found that students face more difficulties with “check all that apply” types of problems. Moreover, Algebra II was the most difficult subject for students. The proposed method can be utilised to improve students’ learning experiences, and the insights from this study can be integrated into mathematics courses to enhance students’ learning outcomes. The code and implementation is available athttps://www.kaggle.com/code/nargesrohani/clicktree/notebook.
Keywords
1. Introduction
In recent years, massive amounts of log data have been collected from students’ interactions with online courses, providing researchers with valuable information for analysing student behaviour and its impact on academic performance (Yi et al., 2018, Aljohani et al., 2019). By examining clickstream data, educators can gain deeper insights into students’ study habits, navigation patterns, and levels of engagement (Wen and Rose, 2014, Li et al., 2020, Matcha et al., 2020, Rohani et al., 2022, Rohani et al., 2024). This knowledge helps identify areas where students may be struggling or be disengaged, allowing for timely intervention and personalised support (Matcha et al., 2020, Matcha et al., 2019). Moreover, clickstream data analysis enables educators to identify effective learning patterns, strategies, and types of educational resources that influence student performance (Aljohani et al., 2019, Rohani et al., 2022, Rohani et al., 2024).
By using the power of educational data mining and artificial intelligence, teachers can use knowledge tracing approaches to monitor students’ understanding levels and predict their future performance, such as their grades (Wang et al., 2023). Students’ performance can be predicted by analysing their past learning activities, particularly their responses to previous assessments (Wang et al., 2023). Knowledge tracing can provide insights about student learning behaviour that can help teachers optimise their teaching approaches in line with students’ needs (Wang et al., 2023). Moreover, this knowledge can provide students with personalised feedback that can enhance the student learning experience and ultimately improve their outcomes (Schumacher and Ifenthaler, 2018, Jang et al., 2022, Koedinger et al., 2013). In line with this aim, the Educational Data Mining (EDM) Cup 2023 (Prihar and Heffernan, 2023) was launched as a competition to predict students’ end-unit-assignment scores in math problems collected from the ASSISTments online platform (Heffernan and Heffernan, 2014). The EDM Cup provided access to a very big clickstream dataset, including millions of student actions, as well as curriculum data, to predict students’ end-unit-assignment scores based on their actions during in-unit assignments (Prihar and Heffernan, 2023).
In related work, there are two main types of student performance prediction tasks: program-level and course-level (Cui et al., 2019, Namoun and Alshanqiti, 2021, Liu et al., 2023). Program-level approaches focus on predicting student dropouts or graduation probabilities from a degree program, while course-level approaches aim to predict students’ scores, grades, or pass/fail status in specific courses (Lemay and Doleck, 2022). For instance, in a program-level prediction study, Oztekin (Oztekin, 2016) developed a hybrid educational data mining approach utilising decision trees, artificial neural networks, and support vector machines to predict the probability of college degree completion. Their findings revealed that factors such as the average fall term score, housing status, and high school performance, significantly influenced the prediction accuracy.
On the other hand, course-level prediction tasks often aim to identify at-risk students who are more likely to fail and provide timely interventions to help them succeed (Akçapınar et al., 2019, Akram et al., 2019). In other words, predictive analysis at the course-level offers valuable insights for enhancing teaching and learning, enabling instructors to understand student behaviour, design effective instruction, and provide targeted support for individual courses (Akram et al., 2019, Oliva-Cordova et al., 2021). For instance, in a previous study (Rohani et al., 2023), we proposed a model that combines Markov chain and neural networks to utilise a range of student activities, including student interactions with video lectures in a Massive Open Online Course (MOOC), in order to predict final student performance after seven days of first engaging with the course. Additionally, we provided students with automatic personalised feedback at an early stage.
In recent years, clickstream data has gained significant attention as a valuable source for course-level performance prediction (Rohani et al., 2023, Kőrösi and Farkas, 2020). This type of data captures students’ learning behaviours, such as accessing different educational resources or taking assessments that offer rich information regarding student interaction within the online course environment (Yürüm et al., 2023, Baker et al., 2020). However, converting millions of clickstream data entries into meaningful features that can accurately predict student performance is challenging (Prihar and Heffernan, 2023, Kőrösi and Farkas, 2020, Asadi et al., 2023).
There are two approaches to utilising clickstream data for performance prediction: using raw data (Asadi et al., 2023, Kőrösi and Farkas, 2020) or employing feature engineering (Rohani et al., 2023). The first method involves employing deep learning methods, which can automatically extract useful features for prediction from raw data. For example, Gábor Kőrösi et al. (Kőrösi and Farkas, 2020) utilised Recurrent Neural Networks (RNNs) to predict student performance at the end of a MOOC, leveraging raw clickstream data from 130,000 students. They showed that their method can accurately predict student performance on Stanford Lagunita’s MOOC dataset without the need for hand-crafted features. Another study with a similar objective conducted an analysis using a larger number of datasets for their evaluation (Asadi et al., 2023). Asadi et al. (Asadi et al., 2023) proposed a method employing graph neural networks to predict student performance by directly analysing raw, multi-dimensional clickstream data without relying on feature extraction. They applied their methodology on 23 MOOCs and, upon evaluation, they found that it has comparable performance to models that use features engineered by humans. In a more recent study, Al-azazi and Ghurab (Al-azazi and Ghurab, 2023) developed a methodology called Artificial Neural Network and Long Short-Term Memory (ANN-LSTM) which is a type of RNN methods. They trained their model on clickstream data of a MOOC to predict student performance at an early stage of the course. The proposed ANN-LSTM achieved an accuracy of approximately 70%, outperforming traditional machine learning methods such as Decision Trees, K-nearest neighbours, and even deep learning methods including RNNs and Gated Recurrent Units. The authors (Al-azazi and Ghurab, 2023) discussed that although deep learning methods such as ANN-LSTM can be trained on raw clickstream data, deep learning techniques require powerful computational resources (high processing power and memory) to preprocess the data and prepare it for feeding into the model. The training step of deep learning methods takes a long time, and often it is time-consuming to find the best hyperparameters (Al-azazi and Ghurab, 2023). Deep learning techniques are also black-box methods that are not easy to interpret and explain, although they can automatically extract nonlinear features (Liang et al., 2021, Al-azazi and Ghurab, 2023, Asadi et al., 2023, Kőrösi and Farkas, 2020).
Given the difficulty in interpreting deep learning-based methods (Swamy et al., 2023), their long training time (Pramod et al., 2021), high computational cost (Pramod et al., 2021), and in some cases lower or equal accuracy compared to traditional predictive models (Asadi et al., 2023), some studies prefer to manually craft easily understandable features from clickstream data (Rohani et al., 2023, López Zambrano et al., 2021, Namoun and Alshanqiti, 2021). They then utilise traditional and simple models to predict student performance (Rohani et al., 2023, López Zambrano et al., 2021, Namoun and Alshanqiti, 2021). For example, Brahim (Brahim, 2022) proposed a predictive model that used a total of 86 new statistical features extracted from log data of a computer engineering course from the Digital Electronics Education and Design Suite (DEEDS) platform. These data were systematically grouped into three categories based on various criteria: (1) type of activity, (2) timing statistics, and (3) count of peripheral activities. These features were preprocessed during the feature selection process and only the most impactful ones were considered for training the model. Their machine learning model was designed to predict whether a student’s performance would be either low or high. The study employed five widely recognised traditional machine learning classifiers: Random Forest, Support Vector Machine, Naïve Bayes, Logistic Regression, and Multi-Layer Perceptron. Their findings showed that the random forest classifier gave the most accurate prediction, achieving a classification accuracy and F1-score of 97%.
In another study, Qiu et al. (Qiu et al., 2022) introduced a novel pipeline for extracting various behavioural features from clickstream data in order to predict student performance. Their pipeline involves several steps: feature extraction, feature selection, feature fusion, and prediction. To find the best set of features, they classified learning behaviours into multiple categories, ranging from learning preparation behaviours to knowledge acquisition behaviours. Afterwards, they selected eight features to be used for prediction after applying a variance filtering threshold. Finally, they utilised various traditional machine learning classifiers, including Support Vector Machines, Naïve Bayes, K-Nearest Neighbours, and SoftMax, to predict student performance based on 6,272 learners in The Open University Learning Analytics Dataset (OULAD). Their model shows both mobility and stability and among all models, Naïve Bayes achieved the highest accuracy (over 90%) in all evaluation scenarios.
Although previous studies attempted to identify a set of useful features and accurate models for performance prediction, extracting meaningful features from raw clickstream data remains a challenge (Prihar and Heffernan, 2023, Baker et al., 2020). Further research is necessary to process the high volume of raw clickstream data across various disciplines and transform it into meaningful features capable of accurately predicting student outcomes.
This study introduces ClickTree, a tree-based model employing clickstream data, for predicting students’ scores on each mathematical problem of end-unit assignments based on their actions during in-unit assignments. The main contribution of this study is to calculate a novel set of features from millions of student actions in the ASSISTments platform. In other words, a set of features at the student, assignment, and problem levels were extracted to predict student performance with high accuracy. The CatBoost tree algorithm was applied to the extracted features, and the model achieved an Area under the ROC Curve (AUC) score of approximately 79% on test data. ClickTree ranked second in EDM Cup 2023 (Prihar and Heffernan, 2023), demonstrating its potential for accurately predicting students’ outcomes in math courses. Additionally, we explored students’ outcomes in different problem types and topics to identify areas of challenge for the students. Furthermore, the learning behaviours of successful students were compared to those of struggling students, with the aim of uncovering different behavioural patterns between the two groups.
The research questions in this study are:
- Can artificial intelligence predict math students’ end-unit assignment scores with high accuracy using clickstream data?
- Which are the most important features in the math course for predicting students’ scores?
In addition to the above research questions, we also explored types of math problems and subjects that were more difficult for students, as well as differences in behavioural patterns of struggling students compared to successful students in math.
The rest of this paper is organised as follows: Section 2 describes the data provided in EDM Cup 2023 and discusses key aspects of the ClickTree method, including feature extraction, prediction and validation. Section 3 presents the results of our analysis with regard to the above research questions, including the evaluation of the ClickTree method and comparison with state-of-the-art approaches. We discuss the implications of this study in Section 4 and provide some suggestions for improving online education in math courses. We conclude the paper and present future work in Section 5.
2. Material and Method
In this section, we explain the ClickTree methodology used to answer RQ1 (see Figure 1 for a visual overview of ClickTree). It should be noted that basic statistics (e.g. mean and variance) and visualisations (e.g. bar charts) were employed for the rest of the analysis.
2.1. Data Description
The dataset provided in the Educational Data Mining Cup 2023 (Prihar and Heffernan, 2023) contains student clickstream data from the ASSISTments online learning platform (Heffernan and Heffernan, 2014). The dataset includes information about the curricula, assignments, problems, and tutoring offered to the students. ASSISTments is an online tutoring platform that provides access to math problems designed by teachers specifically for students. These problems can be solved by students during school hours or as part of their homework assignments. If students encounter difficulties in solving the problems correctly, they have the option to request hints and guidance (Prihar and Heffernan, 2023).
In addition to assisting students in their learning journey, ASSISTments also serves as a tool to assess student performance and record their actions (Heffernan and Heffernan, 2014, Prihar and Heffernan, 2023). Following is an explanation of the tables available in the dataset:
- Action logs: This table includes students’ interactions with in-unit assignments. For example, requesting a hint, or answering a problem within an in-unit assignment correctly or incorrectly. Note that each in-unit assignment can include multiple problems.
- Training Unit-test Scores: This table contains the binary scores of each student on end-unit assignment problems. End-unit assignments can be considered as final exams, and there are multiple in-unit assignments that students participate in before submitting their end-unit assignments. This table includes students’ binary scores on each problem within an end-unit assignment.
- Evaluation Unit-test Scores: This table contains the same kind of information as the training unit test scores but for the evaluation set of data. This allows for having both training and testing datasets for training and testing the predictor model.
- Assignment Details: This table includes information regarding all assignments, including both in-unit and end-unit assignments. For example, this table shows the sequence of problems in each assignment.
- Sequence Details: This table contains the sequence of problems and information regarding each sequence. For instance, the topic, subject, and grade of those problems.
- Problem Details: This table includes characteristics of each individual problem, for example, the BERT vector of the problem.
More information about the dataset is publicly available on the EDM Cup 2023 Kaggle 1 webpage (Prihar and Heffernan, 2023).
For this study, the dataset was collected from middle school students who used ASSISTments during the academic years of 2019-2023. The log data includes 36,296 students, 56,577 in-unit assignments and 57,361 problems.
| student-id | in-unit-assignment-log-id | actions | end-unit-assignment-log-id | problem-id | score |
|---|---|---|---|---|---|
| S_a | in_x | assignment-started, wrong-response, answer-requested | end_w | P_h | 1 |
| S_a | in_x | assignment-started, wrong-response, answer-requested | end_w | P_f | 0 |
| S_a | in_y | problem-started, correct-response, continue | end_r | P_c | 0 |
For the purpose of the competition, the data consists of end-unit assignments given to each student, with each end-unit assignment having a list of related in-unit assignments previously completed by the same student. To put it simply, each end-unit assignment can be considered as a final exam, consisting of multiple problems (questions) that students should answer. Before attempting the end-unit assignment, students can practice by attempting related in-unit assignments, for which they have the option to request a hint, explanation or the correct answer. We aim to analyse in-unit assignment behaviours to predict whether a student will answer a question in the end-unit assignment correctly or not.
Table 1 shows an example of data extract for a student, \(S_a\). The “Student-id” column shows a unique ID for each corresponding student. The “in-unit-assignment-log-id” demonstrates the identifier of the in-unit assignments that the corresponding student completed before solving the end-unit assignment problems. The “action” column shows the set of actions that a student carried out in the in-unit assignment before taking the end-unit assignment. The “end-unit-assignment-log-id” is the identifier of the end-unit assignment, which can include multiple problems. The “problem-id” column shows the identifiers of problems in end-unit assignments. Our goal is to predict the “score” column, which indicates students’ performance in problems within end-unit assignments. It was set to 1 if the student successfully completed an open-ended response problem or submitted the correct answer on their initial attempt without accessing any tutoring. Otherwise, the score was set to 0.
In other words, in the dataset provided by the competition, there are one or more in-unit assignments assigned to students that the students attempt before taking the end-unit assignment. These in-unit assignments contain a list of problems with various tutoring options, such as requesting hints, explanations, or the full answer. Each row in the dataset corresponds to a problem within an end-unit assignment. In the training set, there are a total of 226,750 rows, with 42% of them having a score of 0 and 58% with a score of 1. The validation set has the same label ratio, containing 225,689 rows. The test set comprises 124,455 rows, with unknown scores. We created the validation set in a way that it includes half of the students from the training set and there is no overlap between the students in the training and validation set. The test set was provided by the competition.
The clickstream data of students in in-unit assignments can include several possible actions. A student can start and finish an assignment or a problem, give a correct or wrong answer, submit an open response, continue to the next problem, resume the assignment, and depending on the available tutoring options, they may request a hint, explanation, or full answer to be displayed. Additionally, students may also ask for a live chat session with a tutor or request a video explaining the skill required to solve the problem.
Furthermore, each problem is associated with its text content represented by the BERT embedding (Prihar and Heffernan, 2023, Devlin et al., 2019), along with a description of its skill code as additional information. The problems can be categorised into 10 different types:
- Number: The answer should include only a number, with no letters or mathematical symbols.
- Algebraic Expressions: The answer may consist of a combination of numbers, letters, and mathematical symbols.
- Numeric Expression: The answer should contain numbers and symbols.
- Check All That Apply: The student must select a subset of answers from a given set.
- Multiple Choice: The student must choose one answer from a set of options.
- Exact Match (case sensitive, ignore case): The student is required to submit an answer that precisely matches the correct answer. In the case of “ignore case,” the distinction between lowercase and uppercase letters is not considered for the correct answer.
- Exact Fraction: The answer should be a fraction where both the numerator and denominator must match the correct answer exactly. It is important to note that even if the student’s answer can be simplified to the correct fraction, it would be considered incorrect in this problem type if it does not exactly match the desired fraction.
- Ordering: The task is to arrange a given set in the correct order.
- Ungraded Open Response: The student is asked to upload their answer as plain text or possibly provide a voice or video explanation.
Another important feature is the “sequence,” which represents a set of problems that can be assigned to students by a teacher. Each end-unit or in-unit assignment has a sequence of problems, with each sequence having 5 levels (of which only 4 levels were used in this study). The first level specifies the curriculum, with values including the Kendall Hunt Illustrative Mathematics curriculum or the Engage New York mathematics curriculum (Prihar and Heffernan, 2023). The second level indicates the grade and subject (16 categories), while the third level denotes the unit within the sequence (136 categories). The fourth level specifies the particular subject within the unit (1609 categories). For example, the sequence levels 1, 2, 3, and 4 of an assignment are Kendall Hunt Illustrative Mathematics, Grade 7, Introducing Proportional Relationships, and Spanish Assessments respectively.
There is another categorical feature called problem skill description (487 categories), which provides brief information about the skills required to solve the corresponding problem. More information about the dataset and descriptions of the aforementioned information can be found in (Prihar and Heffernan, 2023).
2.2. Feature Extraction
The clickstream data contains raw features that reflect students’ learning actions in in-unit
assignments, making it an excellent source for extracting meaningful features correlated
to their performance. After preliminary exploration of the dataset (results are available at
https://www.kaggle.com/code/nargesrohani/clicktree/notebook), we extracted
various types of features based on the possible action that a student can take. It should be noted that all
the features presented below were calculated separately for each action (e.g. problem start, problem
finish, and so on).
-
Assignment-level, action counts: To calculate this feature, we explored the action logs of in-unit assignments associated with a specific end-unit assignment and calculated the count of each action (e.g. starting assignment, finishing assignment, continue and so on) performed during those in-unit assignments. The value of this feature remains the same for all problems within the same assignment. As an example, let us calculate this feature for the “hint requested” action. Suppose that we have the following sequence of actions:
\(S_a\) \(in_x\) \(P_h\) \(end_w\) problem started
\(S_a\) \(in_x\) \(P_o\) \(end_w\) hint requested
\(S_a\) \(in_x\) \(P_c\) \(end_w\) hint requested
\(S_a\) \(in_y\) \(P_h\) \(end_w\) wrong response
\(S_a\) \(in_z\) \(P_h\) \(end_w\) hint requested
\(S_a\) \(in_j\) \(P_o\) \(end_r\) hint requested
\(S_b\) \(in_k\) \(P_v\) \(end_m\) hint requested
\(S_b\) \(in_t\) \(P_n\) \(end_m\) hint requested
where \(S\), \(in\), \(P\), and \(end\) represent the identifiers of a student, an in-unit-assignment, a problem within that in-unit-assignment, and an end-unit-assignment respectively. Then the feature for the “hint requested” action for the end-unit-assignment \(end_w\) equals 3.
- Student-level, action counts: Since a student may have completed multiple in-unit assignments, it is worth taking into account the count of each action performed by a student. It is important to note that the value of this feature remains constant for all rows in the dataset where the same student is involved in the assignment. For instance, the value of this feature is 4 for the “hint requested” action of student \(S_a\) based on the aforementioned sequence of actions for student \(S_a\).
- Assignment level, In-unit average action counts: For every in-unit assignment associated with an end-unit assignment, we calculated the total count of a specific action and then computed the average across all the in-unit assignments linked to that end-unit assignment. Consider again the aforementioned sequence of actions. The corresponding in-unit assignments for \(end_w\) are \(in_x\), \(in_y\), and \(in_z\), having the total hint requested action counts of \(2\), \(0\), and \(1\) respectively. Therefore, the value of this feature for the “hint requested” action of \(end_w\) is equal to \((2+0+1)/3=1\).
-
Problem-level, average action counts: Given that the problems within an assignment can vary in difficulty, it is important to take into account the difficulty of each assignment/problem and how students typically respond to them. This includes considering the likelihood of students providing correct or incorrect responses, as well as their tendency to request hints for those problems. Therefore, for each end-unit assignment, we followed a number of steps to calculate its difficulty based on the included problems.
Firstly, for each possible action and problem within an in-unit assignment of an end-unit assignment, we calculate the total count of a specific action (e.g., hint requested) for that specific problem across the entire clickstream data. For instance, based on the above-provided sequence of data for student \(S_a\), problem \(P_h\) and the “hint requested” action, the output is equal to 1 because the hint was requested once for \(P_h\) in the entire dataset. This number reflects the general difficulty of the problem, regardless of specific students or assignments.
Next, for each in-unit assignment, we calculate the average of the values obtained for each problem within the in-unit assignment. For example, the in-unit assignment \(in_x\) consists of the problems \(P_h\), \(P_o\), \(P_c\) with the total hint requested action counts of \(1\), \(2\), \(1\) in the entire clickstream data, so the output value of this step for the “hint requested” action of \(in_x\) would be \((1+2+1)/3 = 4/3\). This calculation is applied to all in-unit assignments within an end-unit assignment, resulting in one number corresponding to each in-unit assignment. The output values indicate assignments’ difficulty based on the problems they contain.
Finally, we calculate the average count of these numbers across all the in-unit assignments associated with a particular end-unit assignment. This process provides an overall assessment of the end-unit assignment’s difficulty, considering the difficulties of its corresponding in-unit assignments (see Figure 2).
Figure 2: Algorithm for calculating problem-level average action count features. -
Problem-level, problem-weighted in-unit average: When a student provides a correct response to a problem, the significance of this action can vary depending on the difficulty of the problem or, in other words, based on the proportion of students who typically gave the correct response to that problem. To capture this significance, it is useful to incorporate a weighted measure that considers the importance of any action within a problem.
We defined the following simple function, \(D(x)\), with \(x\) as an input to calculate the importance of an action for a problem: \begin {align} \label {formula1} D(x) = \begin {cases} \frac {1}{x}& x \neq 0 \\ 0 & x =0 \end {cases} \end {align}
We applied the function \(D\) to the number of occurrences of action \(a\) within problem \(p\), replacing \(x\) with \(N_a{(p)}\). The calculation follows the below formula, where \(u\) refers to a end-unit assignment, \(r\) refers to a in-unit assignment within the end-unit assignment \(u\), and \(N\) denotes the number of occurrences. For example, \(N_a{(p)}\) represents the number of times action \(a\) occurred withing problem \(p\). The following formula multiplies a weight, calculated by Formula \eqref{formula1}, by the frequency of an action within a problem within an in-unit assignment of an end-unit assignment.
\begin {equation} \label {formula2} D(N_a{(p)}) \times N_a(u,r,p). \end {equation} The final feature is calculated by averaging the above measure across all problems within an in-unit assignment, and then across all in-unit assignments within an end-unit assignment (similar to the previous features explained in Figure 2). The measure is designed to be smaller, according to the definition of the \(D\) function, Formula \eqref{formula1}, when the action is more insignificant. It should be noted that this feature takes the importance of an action for a problem into account by considering the overall impact of the action based on the students who carried it out. However, the previous feature, Problem-level average action counts, focused on the importance of an action based on the included problems and their difficulties in an assignment, because each assignment contains different problems.
-
Problem-level performance: This feature was calculated similarly to the two previous features, but the focus here is only on wrong and correct answering actions. For a given in-unit assignment \(r\) within an end-unit assignment \(u\), and a problem \(p\), the following function (correct and wrong answering actions were considered as \(a\) value in Formula \eqref{formula2}) measures the performance of a student in a problem inside an assignment: \begin {align} \chi (u,r,p) = D(N_\text {correct}{(p)}) \times N_{\text {correct}}(u,r,p) - D(N_\text {wrong}{(p)}) \times N_{\text {wrong}}(u,r,p) \end {align}
To give a measure of their performance inside an in-unit assignment, sum \(\chi (u,r,p)\) over all problems \(p\) inside the assignment. At the end, it takes the average of the student’s performance throughout the in-unit assignments corresponding to the end-unit assignment.
- Other features: We have utilised a total of five categorical features in our analysis, namely, “problem type” and “sequence levels 1 to 4”. Additionally, we have included the first 32 principal components of the BERT embedding of the unit problems as additional features.
During the feature selection phase, we eliminated features that had a Pearson correlation higher
than 90% (further information about the extracted and removed features can be found at
https://www.kaggle.com/code/nargesrohani/clicktree/notebook).
2.3. Performance Predictor
The scores of students in problems within end-unit assignments were predicted by the CatBoost classifier (Prokhorenkova et al., 2018) using the novel set of features explained above. CatBoost is an efficient modification of gradient boosting methods (Friedman, 2001, Shyam et al., 2020) that has the ability to handle categorical features without having the curse of dimensionality and target leakage issues (Prokhorenkova et al., 2018, Jabeur et al., 2021, Shyam et al., 2020). CatBoost consists of two main steps (Prokhorenkova et al., 2018, Shyam et al., 2020, Hancock and Khoshgoftaar, 2020): 1 - Pre-processing step: This step involves the efficient conversion of categorical features into numerical values known as Ordered Target Statistics (OTS) (Prokhorenkova et al., 2018). This conversion ensures that the categorical information is effectively incorporated into the model during training. 2 - Gradient boosting step (Friedman, 2001, Hancock and Khoshgoftaar, 2020): In this step, both the numerical features and the Target Statistics (TS) values of categorical features are used as input to build a gradient boosting model. This model utilises the decision trees model as the base predictors, leveraging the combined information from numerical and categorical features (Prokhorenkova et al., 2018, Hancock and Khoshgoftaar, 2020).
These steps are further elaborated in the subsequent subsections by providing a more detailed explanation of how the CatBoost classifier predicts student performance based on the set of numerical and categorical features. Comprehensive information about the CatBoost classifier and gradient boosting methodology can be found in (Prokhorenkova et al., 2018, Hancock and Khoshgoftaar, 2020, Shyam et al., 2020).
2.3.1. Computing Ordered Target Statistics
In general, one-hot encoding or numerical encoding is typically employed to preprocess categorical features and use them in training models (Chapelle et al., 2014, Micci-Barreca, 2001, Seger, 2018). However, when dealing with high-cardinality features, such as the problem skill feature in our dataset, which has 345 different categories, one-hot encoding becomes infeasible (Prokhorenkova et al., 2018, Shyam et al., 2020). On the other hand, the TS method (Prokhorenkova et al., 2018, Hancock and Khoshgoftaar, 2020) involves mapping categories to a reduced number of clusters based on their expected target value and then applying one-hot encoding to these clusters (Prokhorenkova et al., 2018, Micci-Barreca, 2001). Nevertheless, this method suffers from target leakage (Prokhorenkova et al., 2018). To overcome this issue, CatBoost adopts a permutation-based approach to compute ordered TS that solves the issue with target leakage and overfitting (Prokhorenkova et al., 2018).
The computation of the OTS value for a categorical feature in the \(i\)th sample relies only on the targets (binary values of students’ scores) of previously seen samples (samples \(1, \ \cdots , i-1\)), and does not depend on the target of the \(i\)th sample (Prokhorenkova et al., 2018). This eliminates the problem of target leakage (Prokhorenkova et al., 2018). The technique that CatBoost uses to fit data to the base tree models is by making an arbitrary order so as to manage overfitting (note that CatBoost does not take any temporal order in the data into account.) (Prokhorenkova et al., 2018, Hancock and Khoshgoftaar, 2020). A permutation \(\sigma \) is applied to the samples (each pair of problem and end-unit assignment) to introduce an artificial order. Let \(x_k^i\) denote the \(i\)th categorical feature for the \(k\)th problem-assignment pair. The TS value for \(x_{\sigma (k)}^i\) is denoted as \(\hat {x}_{\sigma (k)}^i\) and is calculated using Formula \eqref{ts}. In simple language, the sigma permutation function in Formula \eqref{ts} shuffles the data to prevent overfitting. The function randomly reorders the dataset by changing any inherent order that might cause the model to learn patterns. The output of this function is the same dataset but with the order of the data points changed.
\begin {equation} \label {ts} \hat {x}_{\sigma (k)}^i = \frac {\sum _{j=1}^{i-1}\mathds {1}_{{x_{\sigma (k)}^i = x_{\sigma (j)}^i}}.y_{\sigma (j)} + \alpha P}{\sum _{j=1}^{i-1}\mathds {1}_{{x_{\sigma (k)}^i = x_{\sigma (j)}^i}}+ \alpha } \end {equation}
Here, \(\alpha > 0\) represents a weight parameter, and \(P\) denotes the average target (score) value across all training samples. To address the issue of higher variance in OTS values among preceding samples compared to later samples when using a single permutation, multiple random permutations (\(s\) permutations) were applied to the problem-assignment pairs. For each permutation \(\sigma _r\) (where \(r \in 1,\ \cdots , \ s\)), the corresponding \(\hat {x}_{\sigma _r(k)}^i\) values were calculated and used in the design of the gradient boosting model (Prokhorenkova et al., 2018, Hancock and Khoshgoftaar, 2020).
Let us explain each variable in the formula in more detail:
\(\hat {x}_{\sigma (k)}^i\): This variable shows the output OTS value for the \(i\)th categorical feature (for example problem skill feature), specifically for the \(k\)th problem-assignment pair. It is the estimated expected target value for the sample’s categorical feature based on previously seen samples.
\(\sum _{j=1}^{i-1}\mathds {1}_{{x_{\sigma (k)}^i = x_{\sigma (j)}^i}}\): This part of the formula sums up the occurrences of the categorical feature \(x_{\sigma (k)}^i\) being equal to the categorical feature of previous samples \(x_{\sigma (j)}^i\), where \(j\) ranges from 1 to \(i-1\). It counts how many times the same category has been observed before the current sample.
\(\mathds {1}_{x_{\sigma (k)}^i = x_{\sigma (j)}^i}\) equals to 1 if the categorical feature of the \(i\)th sample (\(x_{\sigma (k)}^i\)) is equal to the categorical feature of the \(j\)th previous sample (\(x_{\sigma (j)}^i\)), and 0 otherwise.
\(y_{\sigma (j)}\): This represents the score (0 or 1) value of the \(j\)th pair of problem and end-unit assignment in the permutation \(\sigma \). It’s the actual score value corresponding to the \(j\)th pair of problem and end-unit assignment.
\(\alpha \): A weight parameter that controls the influence of the average score (our target) value \(P\) in the calculation (we set it to the default value, which is 0.1). It adjusts the impact of the average score value relative to the sum of individual score values.
\(P\): It denotes the average score value across all pairs of problem and end-unit assignments in the training data. It provides a baseline expectation for the score value, helping to normalise the contributions of individual target values in the calculation. To explain it through an example, suppose we have the following data:
Categorical feature “Problem type” with categories: “Ordering”, “Matching” and “Multichoice” Target variable indicating student scores in pair of assignments and problems: 1 (pass) or 0 (fail). And let us consider calculating \(\hat {x}_{\sigma (1)}^1\) for the first problem-assignment pair with ”Ordering” as the problem type:
\(\sum _{j=1}^{i-1}\mathds {1}_{{x_{\sigma (k)}^i = x_{\sigma (j)}^i}}\): Since this is the first sample, there are no previous samples to consider, so this part is 0. \(y_{\sigma (j)}\): If, for example, the score value for the first sample is 0, then \(y_{\sigma (j)} = 0\). \(\alpha \): This is a predefined parameter that can be adjusted during model training to control the influence of the average target value. The default value for this variable is set to 0.1.
2.3.2. Building Gradient Boosting Models
The CatBoost classifier applies a Gradient Boosting algorithm with Decision Trees (GBDT) as base predictors to predict the binary score of problem-assignment pairs (Prokhorenkova et al., 2018), in our case indicating whether a student answered the problem of the end-unit assignment correctly or not. The process includes building the base tree predictors and then making the final prediction by aggregating all the base predictors.
During model construction, decision trees (\(M_r\)), were built based on numerical features and OTS features computed using the methodology explained in section 2.3.1. Each tree is grown in a leaf-by-leaf manner, considering various features and combinations of features at each split that capture the relationship between categorical features, such as problem skills, and the target variable (student score) across different permutations, ensuring robustness in modelling. Given the infeasibility of considering all possible combinations of features, a greedy selection process was employed to select feature combinations (Prokhorenkova et al., 2018). In each split, the criterion for split was selected such that it minimises the loss function defined in Formula \eqref{eql2}.
\begin {equation} \label {eql2} L2 = - \sum _{i=1}^{n}w_i \cdot (a_i - g_i)^2 \end {equation}
Here, \(L2\) is the squared error loss function used in the gradient boosting model, which measures the discrepancy between the predicted score and the actual score for each problem-assignment pair. \(w_i\) is the weight assigned to the \(i\)th problem-assignment pair, which accounts for both the output score weight (\(w_i^{(y)}\)) and the input score weight (\(w_i^{(x)}\)). It determines the importance of each problem-assignment pair in the model training process. For each problem-assignment pair \(x_i\) with score \(y_i\), the weight \(w_i\) was computed by multiplying the score weight (output weight: \(w_i^{(y)}\)) and the problem-assignment weights (input weight: \(w_i^{(x)}\)). \(a_i\) is the prediction of the tree for the \(i\)th problem-assignment pair. It represents the model’s prediction of the score variable for the given problem-assignment input. \(g_i\) is the gradient of the loss function based on the tree prediction. It shows the sensitivity of the loss function to changes in the predicted scores. The problem-assignment weights were randomly assigned using Bayesian bootstrap (Rubin, 1981) with a bagging temperature of 0.2, and the output class weights were calculated based on Formula \eqref{classweight}.
\begin {equation} \label {classweight} w_i^{(y)} = \sqrt {\frac {\max _{c=1}^K(\sum _{y_j = c}w_j^{(x)})}{\sum _{y_j = y_i}w_j^{(x)}}} \end {equation}
Where \(w_i^{(y)}\) is the score weight assigned to the \(i\)th problem-assignment pair, which accounts for the distribution of problem-assignment pairs across different classes. It aims to balance the contribution of two score classes (0 and 1) in the model training process. \(K\) is the number of classes in the score variable that is equal to 2. \(w_j^{(x)}\) is the input weight assigned to the \(j\)th problem-assignment pair. As mentioned above, it reflects the importance of each assignment-problem pair in the model training process. \(y_i\) is the target score for the \(i\)th problem-assignment pair, indicating whether the pair was solved correctly or not by the student.
Each tree is constructed leaf by leaf until it reaches the maximum depth or the maximum number of leaves, whichever occurs sooner. The overall loss function for the model is cross-entropy (CE) (De Boer et al., 2005), as defined in Formula \eqref{eqloss}.
\begin {equation} \label {eqloss} CE = -\dfrac {\sum _{i=1}^{n}w_i (y_i \log (p_i) + (1 - y_i) \log (1-p_i))}{ \sum _{i=1}^{n}w_i } \end {equation}
Here, \(y_i\) represents whether the \(i\)th problem-assignment pair is solved correctly or not, and \(p_i\) is the prediction of the model. The model was trained using stochastic gradient Langevin boosting with posterior sampling (Ustimenko and Prokhorenkova, 2021).
After constructing decision trees \(M_1\), ..., \(M_s\) based on OTS values computed using permutations \(\sigma _1\), ..., \(\sigma _s\), an additional permutation \(\sigma _{*}\) was used to compute OTS values for the final prediction and to determine the leaves in the trees. The final prediction for each problem-assignment pair is computed by boosting the predictions of all the models. To avoid overfitting, early stopping is enabled, meaning that the model stops learning when its performance on the validation data does not improve. This approach allows for saving the best-performing model on the validation data, which is subsequently used as the final model for predicting problem-assignment results in the test data.
2.4. Validation
The validation set was constructed to ensure that it includes half of the students from the dataset, and there is no overlap between the students in the training and validation sets. Consequently, every row in the validation set corresponds to a student who is not present in the training data.
To optimise the performance of the CatBoost classifier, we performed hyperparameter tuning within specified ranges. The hyperparameters we focused on were as follows: ‘depth’ with options [3, 1, 2, 6, 4, 5, 7, 8, 9, 10], ‘iterations’ with options [250, 100, 500, 1000], ‘learning_rate’ with options [0.03, 0.001, 0.01, 0.1, 0.2, 0.3], ‘l2_leaf_reg’ with options [3, 1, 5, 10, 100], ‘bagging_temperature’ with options [0.03, 0.09, 0.25, 0.75], and ‘random_strength’ with options [0.2, 0.5, 0.8]. The objective of this tuning process was to increase the AUC value on the validation data. After the initial tuning, we manually fine-tuned the selected hyperparameters.
The best hyperparameters that were ultimately chosen for the model are as follows: n_iterations = 5000, learning_rate = 0.01, use_best_model = True, l2_leaf_reg = 200, depth = 10, score_function = ‘L2’, langevin = True, grow_policy = ‘Lossguide’, auto_class_weights = ‘SqrtBalanced’, eval_metric = ‘AUC’, posterior_sampling = True, bootstrap_type = ‘Bayesian’, bagging_temperature = 0.2, sampling_unit = ‘Object’, and early_stopping_rounds = 100. Other parameters are set as default.
The implementation was carried out using Python 3, along with the following libraries: numpy
1.19.5, pandas 1.3.4, boost 1.1.1, xgboost 1.7.5, and sci-kit-learn 0.24.2. The code was
executed on a computer with 8 CPU cores and 16 GB of RAM. The code is available at:
https://www.kaggle.com/code/nargesrohani/clicktree/notebook
3. Results
In this section, we present the results of our analysis regarding the research questions, including the evaluation of the ClickTree method. We also compare the performance of the method with other traditional machine learning algorithms.
3.1. Which problems were more difficult for students?
Among the different types of problems, ‘Exact match (ignore case)’ with an average score of 0.38, ‘Check all that apply’ with an average score of 0.40, and ‘Ordering’ with an average score of 0.42 had a lower average scores compared to other types of problems (Figure 3.a). This indicates that they were more difficult for students.
Figure 3.b displays the 15 most challenging problems based on the skills required. Problems that require estimating length (average score of 0.06), Line plot - 5th grade fraction (average score of 0.12), measuring length using unit pieces (average score of 0.13), and histograms (average score of 0.14) were found to be more difficult compared to other problem skills.
Based on Figure 3.c, which presents the average scores among different sequence levels/subjects of the assignments, Algebra II with an average score of 0.42, Algebra I with an average score of 0.48, and Geometry with an average score of 0.50, were more challenging for students.
Furthermore, when examining problem subtopics in Figure 3.d, Module 2 - descriptive statistics (average score of 0.22), Unit 6 - multiplying and dividing multi-digit numbers (average score of 0.25), Unit 1 - scale drawings (average score of 0.25), and Unit 5 - multiplicative comparison and measurement (average score of 0.26) were found to be more difficult for students.

3.2. Learning behavior of successful students vs struggling students
Based on our analysis (see Table 2), students who answered the end-unit assignment problems correctly (i.e. successful students) had a higher number of ‘continue selected’, ‘correct response’, ‘problem finished’, and ‘problem started’ actions in in-unit assignments compared to students who could not answer the end-unit assignment problems correctly (i.e. struggling students). On the other hand, struggling students had a higher number of requests for hints and answers. This implies that students who struggle can be identified during their interactions with the in-unit assignments before they take the final end-unit assignment. However, it is important to note that aside from the ‘answer requested’ action, which exhibits a small-to-moderate effect size for the difference, the effect size for the other actions is small. We employed the t-test and Cohen’s D effect size measure to determine whether the means of in-unit action counts for struggling and successful students are significantly different. Actions with a p-value lower than 0.05 and Cohen’s d higher than 0.10 are considered and shown in bold in Table 2.
| Action | Struggling students | Successful students | p-value, Cohen’s d
|
|---|---|---|---|
| answer requested | 18.16 | 11.28 | 0.00, 0.29 |
| assignment finished | 11.10 | 12.32 | 3.79e-220, 0.10 |
| assignment resumed | 7.97 | 8.09 | 0.08, 0.01 |
| assignment started | 13.56 | 14.38 | 3.19e-77, 0.06 |
| continue selected | 101.18 | 117.97 | 0.00,0.19 |
| correct response | 78.43 | 93.16 | 0.00, 0.13 |
| explanation requested | 0.61 | 0.33 | 5.04e-179, 0.09 |
| hint requested | 2.24 | 1.31 | 0.00, 0.13 |
| open response | 33.74 | 37.14 | 5.12e-97, 0.06 |
| problem finished | 112.48 | 130.51 | 0.00, 0.12 |
| problem started | 114.88 | 132.51 | 0.00, 0.11 |
| wrong response | 40.61 | 33.90 | 0.00, 0.14 |
3.3. ClickTree method evaluation and comparison
The ClickTree method achieved an AUC of 0.78844 on the test data and ranked second in the EDM Cup 2023 with only a 0.001 difference from the first-ranked method.
Before using the CatBoost classifier, we applied different traditional classification methods to the extracted features in order to find a model with higher accuracy in predicting students’ end-unit scores. Table 3 presents a comparison with traditional machine learning methods, as well as other techniques that have been previously employed in related work for student performance prediction, such as neural networks (Rohani et al., 2023) and ANN-LSTM (Al-azazi and Ghurab, 2023).
| Method | AUC | AUPR | Accuracy | Precision | Recall | Train time | Test time |
|---|---|---|---|---|---|---|---|
| ClickTree | 0.80 | 0.84 | 0.73 | 0.73 | 0.71 | 26 mins | less than 1 sec |
| XGBoost (Chen and Guestrin, 2016) | 0.78 | 0.82 | 0.72 | 0.72 | 0.72 | 4 mins | less than 1 sec |
| Decision Tree | 0.73 | 0.78 | 0.69 | 0.68 | 0.67 | 8 secs | less than 1 sec |
| Random Forest | 0.76 | 0.80 | 0.70 | 0.70 | 0.67 | 2 mins | 2 secs |
| Logistic Regression | 0.69 | 0.74 | 0.66 | 0.64 | 0.63 | 5 secs | less than 1 sec |
| Neural networks (Rohani et al., 2023) | 0.77 | 0.80 | 0.71 | 0.71 | 0.69 | 14 mins | 12 secs |
| ANN-LSTM (Al-azazi and Ghurab, 2023) | 0.51 | 0.58 | 0.57 | 0.29 | 0.50 | one week | 10 hrs |
The CatBoost classifier outperformed all other models across all criteria except training time. The ClickTree method achieved an AUC of 80% on the validation data, while XGBoost, Random Forest, Decision Tree, Logistic Regression, Neural networks and ANN-LSTM achieved AUC values of 78%, 76%, 74%, 69%, 77%, and 51%, respectively. One can conclude that tree-based methods were more appropriate for the dataset. It should be mentioned that since we had categorical features, the CatBoost classifier, which is well-known for handling categorical data very well (Shyam et al., 2020, Hancock and Khoshgoftaar, 2020), seems to be more suitable and accurate. To use categorical features in the classification by the rest of the methods, we had to employ the numerical label encoding approach to convert the categorical values into unique numerical values (Pedregosa et al., 2011). We also tried using one-hot-encoding (Pedregosa et al., 2011), which converts each categorical variable into a binary vector. This had lower accuracy compared to the numerical encoding approach. Therefore, we selected the numerical label encoding approach to handle categorical features for those methods.
Let us now discuss further how the different methods compare to each other, by considering a range of other perspectives, such as accuracy, training time, computational cost, interpretability, and human effort. In terms of training time, simpler methods like logistic regression and decision trees were the fastest (less than 1 minute) and needed minimal computational resources. Although ClickTree had a higher training time (26 mins) due to boosting several decision trees and using the OTS technique, its training time is still reasonable. Conversely, ANN-LSTM had a significantly longer runtime for both training and testing. It is also costly to tune hyperparameters of deep learning methods (we used the default values reported by (Al-azazi and Ghurab, 2023) study). ANN-LSTM failed to achieve high accuracy, probably due to its oversight in considering features at different levels. This demonstrates the value of feature extraction. Although feature engineering before model training may be time-consuming and need human effort, this time and effort is moderate in comparison to the time required for ANN-LSTM to fit on a new dataset and run on it. Regarding interpretability, traditional machine learning methods, such as logistic regression and decision trees are more straightforward to interpret, while neural networks and ANN-LSTM are not due to their black-box nature (Swamy et al., 2023).
In conclusion, usually, there is a trade-off between high accuracy and other factors, and the selection of the method depends on the dataset and the aim of prediction (Tuvshinjargal and Kim, 2022). In this study, the inclusion of features at different levels (i.e. student, assignment and problem) and the effective utilisation of categorical features were important for achieving high accuracy in EDM Cup 2023. ClickTree showed the best accuracy, acceptable training time and interpretability, and fast test time which makes it the best methodology for predicting problem scores of end-unit assignments in this dataset.
3.4. Feature Importance
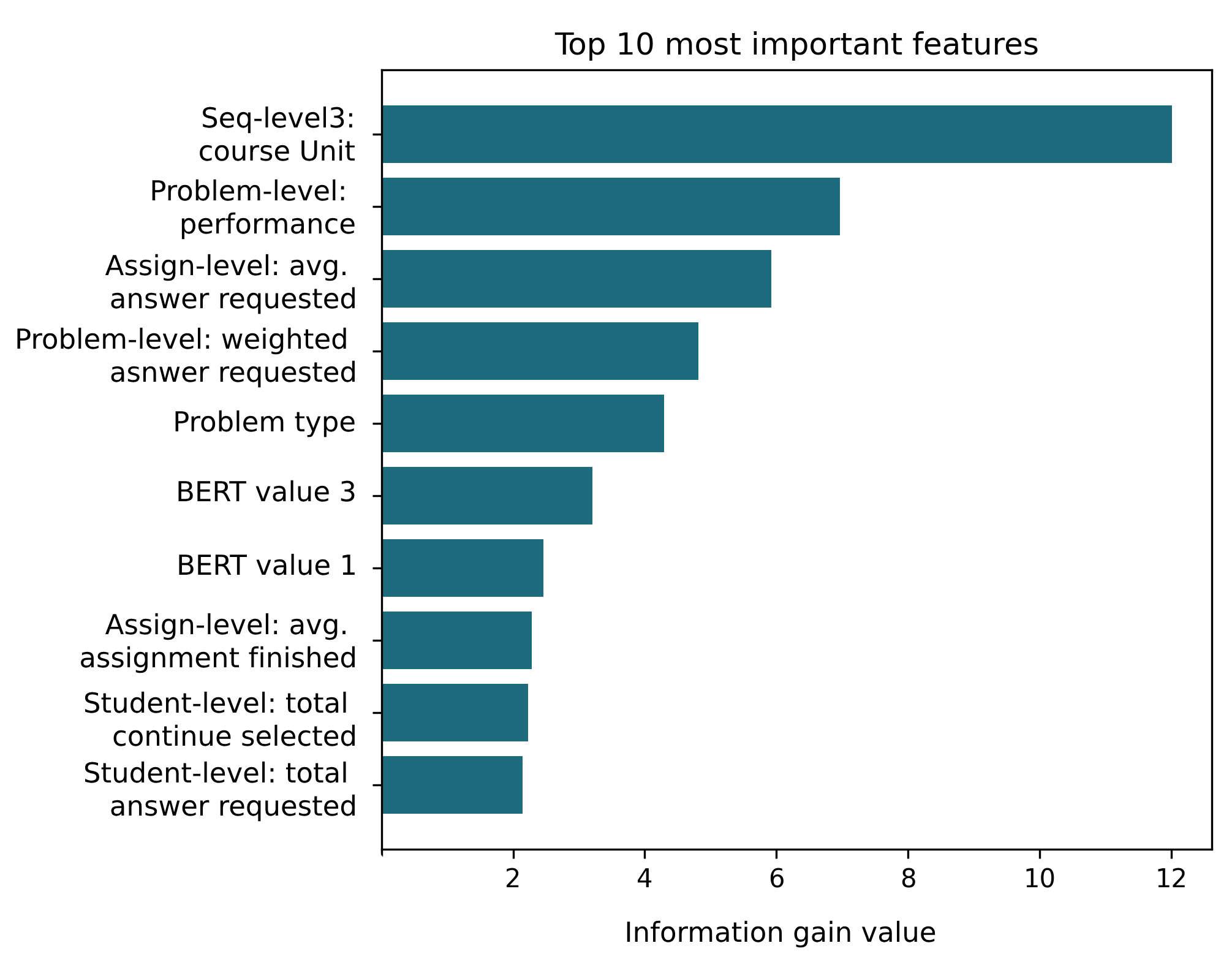
Upon analysing the importance of each feature in increasing the ClickTree predictive model accuracy, we identified the 10 most important ones (see Figure 4). The most important feature is sequence_folder_path_level_3, which represents the subject of the assignment problem. The next most important features are problem level performance, average answer request, weighted answer request, problem type, BERT features calculated from the questions’ text, average assignment finished, total continue of the assignments, and total answer request, respectively (features explained in Section 2.2).
4. Implications and Recommendations
Previous studies (Rohani et al., 2023, Schumacher and Ifenthaler, 2018, Jang et al., 2022, Koedinger et al., 2013) have shown that using computational methods to predict students’ performance can assist in providing timely feedback and support to enhance students’ outcomes. ClickTree contributes to this body of work and can be employed not only on the ASSISTments platform but also on other online platforms to predict students’ performance, thereby helping teachers in delivering tailored feedback and guidance to students.
Similarly to previous studies (Yu and Li, 2011, Choi et al., 2017, Kearns, 2012), our results reveal that certain types of problems are more challenging for students. In particular, problem types such as “Exact match (ignore case),” “Check everything relevant,” and “Ordering” exhibit lower average correct scores, indicating greater difficulty. The challenge in designing effective assessments on online platforms is discussed in the literature (Kearns, 2012), and previous studies note that students use different cognitive processes and demonstrate varying performance based on the question type (Yu and Li, 2011, Choi et al., 2017). For instance, (Riggs et al., 2020, Kearns, 2012) suggest providing preparation exercises for each question type to prepare students for the actual exams. Accordingly, in our analysed course, for the “Exact matching (ignore case)” problem type, additional practice or guided examples can be offered to enhance student understanding of the skills required for this specific problem type.
Also, problems that required skills such as estimating lengths, line plots, measuring lengths by unit pieces, and histograms were found to be more difficult for students. This finding is also mentioned in (Tan Sisman and Aksu, 2016), which discusses students’ misconceptions and errors while solving tasks involving length, area, and volume measurement. To facilitate learning these concepts, virtual manipulation, an interactive visual representation of dynamic objects implemented on the web, can aid in understanding mathematics involving measurement and length. Previous studies have discussed the benefits of this teaching approach for math students (Moyer-Packenham and Westenskow, 2013).
In line with existing literature that discusses the difficulty of algebra and geometry for high school students (Özerem, 2012, Sugiarti and Retnawati, 2019, Chow, 2011), this study also identifies Algebra II, Algebra I, and Geometry as more challenging than other subjects for students. Therefore, by understanding the origin of the difficulty (e.g., a lack of necessary background knowledge), new teaching strategies and resources can be designed to effectively teach these topics (Chow, 2011). For instance, offering creative examples, practice, and interactive activities (Kartika et al., 2019), specifically focusing on the challenging topics (algebra and geometry), can help facilitate student training. Our findings may enable educators to devote more attention and instructional resources to the challenging subjects (algebra and geometry) and sub-subjects (estimating length, line plots, and histograms), ensuring that students receive appropriate support and instruction where needed most (Chow, 2011, Pardo et al., 2019).
Additionally, analysis of students’ behaviour reveals significant differences between successful and struggling students, which is in line with related literature (Hirose, 2018, Matcha et al., 2019). Successful students, who correctly answer the end-unit assignment problems tend to attempt more questions. Struggling students seek more hints and answers, which is in accordance with the help-seeking learning strategy (Newman and Schwager, 1995). This also implies that struggling students can be identified early based on their interactions with in-unit assignments (Rohani et al., 2023). Providing timely personalized support and interventions for these students can enhance their performance in end-unit assignments (Matcha et al., 2019, Rohani et al., 2022, Rohani et al., 2023). Additionally, offering self-directed learning strategies and helpful online tutorials about learning strategies to support students’ independent learning could be beneficial (Matcha et al., 2020, Matcha et al., 2019, Rohani et al., 2023, Cheng, 2011).
To summarise, the aforementioned insights and suggestions from this study can help identify struggling students and implement better teaching approaches to address areas where students face difficulties. The ClickTree method can be used across a range of disciplines to predict students’ final exam scores based on their previous interactions with the course. This can be beneficial for educators, enabling them to provide tailored feedback to students before their final exams. Additionally, insights such as students’ difficulties in measuring length can help math educators improve their teaching methods in challenging areas. Algebra topics need more attention, and using creative examples might benefit students.
5. Conclusion and Future Work
We developed ClickTree, a method for predicting students’ performance on each problem within a math assignment by utilising features extracted from clickstream data. ClickTree calculates a novel set of features at problem-, student- and assignment-levels. After that, it utilises the CatBoost classifier to predict students’ scores in answering the end-unit assignment problems. The developed method achieved an AUC of approximately 79% on test data and ranked second in EDM Cup 2023 with only about a 0.001 difference from the first-ranking submission. Our results show that tree-based methods with a boosting approach had higher accuracy for this dataset compared to other machine learning and deep learning methods, which is also discussed in literature (Ibrahim et al., 2020, Shyam et al., 2020, Hancock and Khoshgoftaar, 2020). The inclusion of multiple levels of features was effective in improving model accuracy, and the BERT vectors, which represent the text of the questions, were also important features for prediction.
Our analysis also reveals that students who started and completed more problems, as well as those who answered more questions correctly during the in-unit assignment, were more likely to answer the final assignment of the unit correctly. On the other hand, struggling students had a higher rate of requesting answers or hints for the problems. We also investigated the types and subjects of problems that were more challenging for students. The results demonstrate that the type of problems where a student must select a subset of answers from a given set (i.e. ‘Check all that apply’) was more difficult for students, and topics such as Algebra II, descriptive statistics, and multiplying and dividing multi-digit numbers were more challenging for students. By considering the insights provided in this paper, course instructors can focus on improving the course and assignments in the subjects (e.g. Algebra and Geometry) and problem areas (e.g. length estimation) that were difficult for students.
While ClickTree achieved high accuracy in predicting student performance using clickstream data, it is important to acknowledge a number of limitations. We only evaluated the method on one dataset; therefore, it is essential to note that the generalisability of the developed method should be evaluated using various courses and datasets in future research. Furthermore, our methodology relied on predefined features extracted from clickstream data that may not be applicable to other datasets where limited raw data about student behaviour is available. Future studies should focus on developing a pipeline that can operate on every type of dataset with available features and dynamically decide about the feature engineering phase.
6. Acknowledgments
This work was supported by the Medical Research Council [grant number MR/N013166/1]. The funder was not involved in the design, execution, or interpretation of this study. We would like to thank the Educational Data Mining Conference for organising EDM Cup 2023. Also, we would also like to express our appreciation to Dr Kobi Gal and Dr Michael Gallagher for their support throughout the writing of this research paper. We would like to extend our appreciation to Dr. Fatemeh Ahmadimoghari for her help in improving the readability of the manuscript for interdisciplinary audiences.
7. Author Contributions
NR and BR contributed to the development of the method. NR and BR generated the results and implemented the method, while AM helped in the interpretation of the results. NR and BR wrote the first draft of the paper and AM assisted in enhancing the written work. All authors read the final version of the paper and approved it.
8. Declaration of generative AI software tools in the writing process
During the revision of this work, NR used ChatGPT by asking it: ”Only improve the grammar and writing and do not change the input text.” in order to improve the readability of the manuscript. The authors have not used the tool for the generation of any text for any section of the manuscript. After using this tool, all authors reviewed and edited the writing again to improve the readability of the manuscript. All authors take full responsibility for the content of the publication.
References
- Akçapınar, G., Altun, A., and Aşkar, P. 2019. Using learning analytics to develop early-warning system for at-risk students. International Journal of Educational Technology in Higher Education 16, 1, 1–20.
- Akram, A., Fu, C., Li, Y., Javed, M. Y., Lin, R., Jiang, Y., and Tang, Y. 2019. Predicting students’ academic procrastination in blended learning course using homework submission data. IEEE Access 7, 102487–102498.
- Al-azazi, F. A. and Ghurab, M. 2023. ANN-LSTM: A deep learning model for early student performance prediction in mooc. Heliyon 9, 4. Article e15382.
- Aljohani, N. R., Fayoumi, A., and Hassan, S.-U. 2019. Predicting at-risk students using clickstream data in the virtual learning environment. Sustainability 11, 24. Article 7238.
- Asadi, M., Swamy, V., Frej, J., Vignoud, J., Marras, M., and Käser, T. 2023. Ripple: Concept-based interpretation for raw time series models in education. In Proceedings of the Association for the Advancement of Artificial Intelligence (AAAI) Conference on Artificial Intelligence, B. Williams, C. Yiling, and J. Neville, Eds. Vol. 37. AAAI Press, 15903–15911.
- Baker, R., Xu, D., Park, J., Yu, R., Li, Q., Cung, B., Fischer, C., Rodriguez, F., Warschauer, M., and Smyth, P. 2020. The benefits and caveats of using clickstream data to understand student self-regulatory behaviors: opening the black box of learning processes. International Journal of Educational Technology in Higher Education 17, 1, 1–24.
- Brahim, G. B. 2022. Predicting student performance from online engagement activities using novel statistical features. Arabian Journal for Science and Engineering 47, 8, 10225–10243.
- Chapelle, O., Manavoglu, E., and Rosales, R. 2014. Simple and scalable response prediction for display advertising. ACM Transactions on Intelligent Systems and Technology (TIST) 5, 4, 1–34.
- Chen, T. and Guestrin, C. 2016. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, B. Krishnapuram, M. Shah, A. Smola, C. Aggarwal, D. Shen, and R. Rastogi, Eds. KDD ’16. Association for Computing Machinery, New York, NY, USA, 785–794.
- Cheng, E. 2011. The role of self-regulated learning in enhancing learning performance. The International Journal of Research and Review 6, 1–16.
- Choi, J., Walters, A., and Hoge, P. 2017. Self-reflection and math performance in an online learning environment. Online Learning Journal 21, 4, 79–102.
- Chow, T.-C. F. 2011. Students’ difficulties, conceptions and attitudes towards learning algebra: an intervention study to improve teaching and learning. Ph.D. thesis, Curtin University.
- Cui, Y., Chen, F., Shiri, A., and Fan, Y. 2019. Predictive analytic models of student success in higher education: A review of methodology. Information and Learning Sciences 120, 3/4, 208–227.
- De Boer, P.-T., Kroese, D. P., Mannor, S., and Rubinstein, R. Y. 2005. A tutorial on the cross-entropy method. Annals of operations research 134, 19–67.
- Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), J. Burstein, C. Doran, and T. Solorio, Eds. Association for Computational Linguistics, Minneapolis, Minnesota, 4171–4186.
- Friedman, J. H. 2001. Greedy function approximation: A gradient boosting machine. The Annals of Statistics 29, 5, 1189 – 1232.
- Hancock, J. T. and Khoshgoftaar, T. M. 2020. Catboost for big data: an interdisciplinary review. Journal of big data 7, 1, 1–45.
- Heffernan, N. T. and Heffernan, C. L. 2014. The assistments ecosystem: Building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. International Journal of Artificial Intelligence in Education 24, 470–497.
- Hirose, H. 2018. Difference between successful and failed students learned from analytics of weekly learning check testing. Information Engineering Express 4, 1, 11–21.
- Ibrahim, A. A., Ridwan, R. L., Muhammed, M. M., Abdulaziz, R. O., and Saheed, G. A. 2020. Comparison of the catboost classifier with other machine learning methods. International Journal of Advanced Computer Science and Applications 11, 11. Article 11.
- Jabeur, S. B., Gharib, C., Mefteh-Wali, S., and Arfi, W. B. 2021. Catboost model and artificial intelligence techniques for corporate failure prediction. Technological Forecasting and Social Change 166. Article 120658.
- Jang, Y., Choi, S., Jung, H., and Kim, H. 2022. Practical early prediction of students’ performance using machine learning and explainable AI. Education and Information Technologies 27, 1–35.
- Kartika, Y., Wahyuni, R., Sinaga, B., and Rajagukguk, J. 2019. Improving math creative thinking ability by using math adventure educational game as an interactive media. In Journal of Physics: Conference Series. Vol. 1179. IOP Publishing, 012078.
- Kearns, L. R. 2012. Student assessment in online learning: Challenges and effective practices. Journal of Online Learning and Teaching 8, 3, 198–208.
- Koedinger, K. R., Brunskill, E., Baker, R. S., McLaughlin, E. A., and Stamper, J. 2013. New potentials for data-driven intelligent tutoring system development and optimization. AI Magazine 34, 3, 27–41.
- Kőrösi, G. and Farkas, R. 2020. MOOC performance prediction by deep learning from raw clickstream data. In Advances in Computing and Data Sciences: 4th International Conference, ICACDS 2020, Valletta, Malta, April 24–25, 2020, Revised Selected Papers 4, M. Singh, P. K. Gupta, V. Tyagi, J. Flusser, T. Ören, and G. Valentino, Eds. Springer, 474–485.
- Lemay, D. J. and Doleck, T. 2022. Predicting completion of massive open online course (MOOC) assignments from video viewing behavior. Interactive Learning Environments 30, 10, 1782–1793.
- Li, Q., Baker, R., and Warschauer, M. 2020. Using clickstream data to measure, understand, and support self-regulated learning in online courses. The Internet and Higher Education 45. Article 100727.
- Liang, Y., Li, S., Yan, C., Li, M., and Jiang, C. 2021. Explaining the black-box model: A survey of local interpretation methods for deep neural networks. Neurocomputing 419, 168–182.
- Liu, Y., Fan, S., Xu, S., Sajjanhar, A., Yeom, S., and Wei, Y. 2023. Predicting student performance using clickstream data and machine learning. Education Sciences 13, 1. Article 17.
- López Zambrano, J., Lara Torralbo, J. A., Romero Morales, C., et al. 2021. Early prediction of student learning performance through data mining: A systematic review. Psicothema 33, 3, 456–465.
- Matcha, W., Gasevic, D., Uzir, N. A., Jovanovic, J., Pardo, A., Lim, L., Maldonado-Mahauad, J., Gentili, S., Perez-Sanagustin, M., and Tsai, Y.-S. 2020. Analytics of learning strategies: Role of course design and delivery modality. Journal of Learning Analytics 7, 2, 45–71.
- Matcha, W., Gašević, D., Uzir, N. A., Jovanović, J., and Pardo, A. 2019. Analytics of learning strategies: Associations with academic performance and feedback. In Proceedings of the 9th International Conference on Learning Analytics & Knowledge. LAK19. Association for Computing Machinery, New York, NY, USA, 461–470.
- Micci-Barreca, D. 2001. A preprocessing scheme for high-cardinality categorical attributes in classification and prediction problems. ACM SIGKDD Explorations Newsletter 3, 1, 27–32.
- Moyer-Packenham, P. S. and Westenskow, A. 2013. Effects of virtual manipulatives on student achievement and mathematics learning. International Journal of Virtual & Personal Learning Environments 4, 3, 35–50.
- Namoun, A. and Alshanqiti, A. 2021. Predicting student performance using data mining and learning analytics techniques: A systematic literature review. Applied Sciences 11, 1. Article 237.
- Newman, R. S. and Schwager, M. T. 1995. Students’ help seeking during problem solving: Effects of grade, goal, and prior achievement. American Educational Research Journal 32, 2, 352–376.
- Oliva-Cordova, L. M., Garcia-Cabot, A., and Amado-Salvatierra, H. R. 2021. Learning analytics to support teaching skills: A systematic literature review. IEEE Access 9, 58351–58363.
- Özerem, A. 2012. Misconceptions in geometry and suggested solutions for seventh grade students. Procedia-Social and Behavioral Sciences 55, 720–729.
- Oztekin, A. 2016. A hybrid data analytic approach to predict college graduation status and its determinative factors. Industrial Management & Data Systems 116, 8, 1678–1699.
- Pardo, A., Jovanovic, J., Dawson, S., Gašević, D., and Mirriahi, N. 2019. Using learning analytics to scale the provision of personalised feedback. British Journal of Educational Technology 50, 1, 128–138.
- Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E. 2011. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research 12, 2825–2830.
- Pramod, A., Naicker, H. S., and Tyagi, A. K. 2021. Machine Learning and Deep Learning: Open Issues and Future Research Directions for the Next 10 Years. John Wiley Sons, Ltd, Chapter 18, 463–490.
- Prihar, E. and Heffernan, N.
2023. EDM cup 2023.
https://kaggle.com/competitions/edm-cup-2023. Accessed: 2024-07-12. - Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V., and Gulin, A. 2018. Catboost: unbiased boosting with categorical features. Advances in neural information processing systems 31, 6639–6649.
- Qiu, F., Zhang, G., Sheng, X., Jiang, L., Zhu, L., Xiang, Q., Jiang, B., and Chen, P.-k. 2022. Predicting students’ performance in e-learning using learning process and behaviour data. Scientific Reports 12, 1, 453. Article 453.
- Riggs, C. D., Kang, S., and Rennie, O. 2020. Positive impact of multiple-choice question authoring and regular quiz participation on student learning. CBE—Life Sciences Education 19, 2. Article ar16.
- Rohani, N., Gal, K., Gallagher, M., and Manataki, A. 2022. Discovering students’ learning strategies in a visual programming MOOC through process mining techniques. In International Conference on Process Mining, M. Montali, A. Senderovich, and M. Weidlich, Eds. Springer, 539–551.
- Rohani, N., Gal, K., Gallagher, M., and Manataki, A. 2023. Early Prediction of Student Performance in a Health Data Science MOOC. In Proceedings of the 16th International Conference on Educational Data Mining, M. Feng, T. Käser, and P. Talukdar, Eds. International Educational Data Mining Society, 325–333.
- Rohani, N., Gal, K., Gallagher, M., and Manataki, A. 2024. Providing insights into health data science education through artificial intelligence. BMC Medical Education 24. Article 564.
- Rubin, D. B. 1981. The Bayesian Bootstrap. The Annals of Statistics 9, 1, 130 – 134.
- Schumacher, C. and Ifenthaler, D. 2018. Features students really expect from learning analytics. Computers in human behavior 78, 397–407.
- Seger, C. 2018. An investigation of categorical variable encoding techniques
in machine learning: binary versus one-hot and feature hashing.
https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1259073&dswid=-2863. Accessed: 2024-07-12. - Shyam, R., Ayachit, S. S., Patil, V., and Singh, A. 2020. Competitive analysis of the top gradient boosting machine learning algorithms. In 2020 2nd International Conference on Advances in Computing, Communication Control and Networking (ICACCCN), V. Sharma, R. Srivastava, and M. Singh, Eds. IEEE, 191–196.
- Sugiarti, L. and Retnawati, H. 2019. Analysis of student difficulties on algebra problem solving in junior high school. In Journal of Physics: Conference Series, A. M. Abadi, A. Wijaya, and J. A. Vallejo, Eds. Vol. 1320. IOP Publishing, 012103.
- Swamy, V., Du, S., Marras, M., and Kaser, T. 2023. Trusting the explainers: teacher validation of explainable artificial intelligence for course design. In LAK23: 13th International Learning Analytics and Knowledge Conference, S. Joksimovic, A. Barthakur, I. Hilliger, H. Khosravi, B. Rienties, and S. Dawson, Eds. Association for Computing Machinery, 345–356.
- Tan Sisman, G. and Aksu, M. 2016. A study on sixth grade students’ misconceptions and errors in spatial measurement: Length, area, and volume. International Journal of Science and Mathematics Education 14, 1293–1319.
- Tuvshinjargal, A. and Kim, E. 2022. ML vs DL: Accuracy and testing runtime trade-offs in BCI. In International Conference on Human-Computer Interaction, M. Kurosu, S. Yamamoto, H. Mori, D. D. Schmorrow, C. M. Fidopiastis, N. A. Streitz, and S. Konomi, Eds. Springer, 497–511.
- Ustimenko, A. and Prokhorenkova, L. 2021. Sglb: Stochastic gradient langevin boosting. In International Conference on Machine Learning, N. Lawrence, Ed. PMLR, 10487–10496.
- Wang, F., Huang, Z., Liu, Q., Chen, E., Yin, Y., Ma, J., and Wang, S. 2023. Dynamic cognitive diagnosis: An educational priors-enhanced deep knowledge tracing perspective. IEEE Transactions on Learning Technologies 16, 3, 306–323.
- Wen, M. and Rose, C. P. 2014. Identifying latent study habits by mining learner behavior patterns in massive open online courses. In Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management, J. Li, X. S. Wang, M. Garofalakis, I. Soboroff, T. Suel, and M. Wang, Eds. CIKM ’14. Association for Computing Machinery, New York, NY, USA, 1983–1986.
- Yi, J. C., Kang-Yi, C. D., Burton, F., and Chen, H. D. 2018. Predictive analytics approach to improve and sustain college students’ non-cognitive skills and their educational outcome. Sustainability 10, 11. Article 4012.
- Yu, F. and Li, M. 2011. Effects of different types of online student question-generation on learning. In Proceedings of the 19th International Conference on Computers in Education, ICCE 2011, R. Mizoguchi, O. Sitthisak, T. Hirashima, G. Biswas, T. Supnithi, and F.-Y. Yu, Eds. Proceedings of the 19th International Conference on Computers in Education, ICCE 2011. 768–770.
- Yürüm, O. R., Taşkaya-Temizel, T., and Yıldırım, S. 2023. The use of video clickstream data to predict university students’ test performance: A comprehensive educational data mining approach. Education and Information Technologies 28, 5, 5209–5240.