Abstract
We propose a novel model, Wide & Deep Item Response Theory (Wide & Deep IRT), to predict the correctness of students’ responses to questions using historical clickstream data. This model combines the strengths of conventional Item Response Theory (IRT) models and Wide & Deep Learning for Recommender Systems. By leveraging clickstream data, Wide & Deep IRT provides precise predictions of answer correctness while enabling the exploration of behavioral patterns among different ability groups. Our experimental results based on a real-world dataset (EDM Cup 2023) demonstrate that Wide & Deep
IRT outperforms conventional IRT models and state-of-the-art knowledge tracing models while
maintaining the ease of interpretation associated with IRT models. Our model performed very well in the
EDM Cup 2023 competition, placing second on the public leaderboard and third on the private
leaderboard. Additionally, Wide & Deep IRT identifies distinct behavioral patterns across ability
groups. In the EDM Cup 2023 dataset, low-ability students were more likely to directly request
an answer to a question before attempting to respond, which can negatively impact their learning
outcomes and potentially indicates attempts to game the system. Lastly, the Wide & Deep IRT model
consists of significantly fewer parameters compared to traditional IRT models and deep knowledge
tracing models, making it easier to deploy in practice. The source code is available via Open Science
Framework.1
Keywords
1. Introduction
Modeling a student’s knowledge or ability based on their interaction with a learning platform is an essential task for today’s learning systems. For instance, a tutoring system based on mastery learning must assess students’ understanding of a concept before advancing to the next one (Ritter et al., 2016). Similarly, a test preparation application needs to evaluate students’ abilities in order to suggest suitable items (Loh et al., 2021). Personalized language learning platforms require an analysis of each student’s rate of forgetting to recommend timely vocabulary review (Settles and Meeder, 2016, Lindsey et al., 2014). Additionally, colleges need to track students’ academic progress to identify those at risk of falling behind, allowing instructors to intervene promptly (Pistilli and Arnold, 2010). A widely accepted approach, knowledge tracing, tackles this issue as a sequential prediction problem, aiming to accurately predict the correctness of a student’s answer to the immediate subsequent question based on their historical interactions with the learning platform. This approach, which can be traced back to Corbett and Anderson (1994), has attracted significant research interest in recent years due to the rise in popularity of online learning platforms. Recent advancements in this field predominantly center around incorporating novel deep learning models (Ghosh et al., 2020, Nakagawa et al., 2019, Piech et al., 2015, Pu et al., 2020, Zhang et al., 2017).
However, it remains unclear whether predicting the correctness of a student’s response to the next question is the best approach to modeling their ability, because the correctness of a student’s response is not influenced only by their ability. For example, low engagement behaviors, such as rapid guessing (Wise, 2017), may negatively impact students’ immediate performance; however, these behaviors are not reliable indicators of low abilities. Hence, if two models have equal capacity to model students’ ability, but one can infer students’ engagement based on their most recent question-answering performance while the other cannot, then the model capable of inferring engagement is considered superior for the knowledge tracing task. This holds true even if both models are equally capable of modeling student ability. Scruggs et al. (2020) and (2023) articulated a similar argument, emphasizing that it is more crucial to measure the volume of knowledge students retain after using the learning system, rather than their immediate success within the system. They discovered that models excelling at the knowledge tracing task do not necessarily perform well at modeling students’ abilities, which are estimated based on post-test scores after using a learning environment.
We propose that predicting students’ performance on a post-test offers a more accurate model of students’ abilities than merely predicting the correctness of their next answer. This approach could help eliminate factors that fluctuate over time, such as engagement. However, this method relies heavily on the availability of high-quality data that includes post-test information. In this study, we utilize a recent dataset, the EDM Cup 2023, which provides students’ clickstream data from math unit assignments and test assignments as post-test data. The availability of clickstream data makes EDM Cup 2023 especially valuable, as previous research has demonstrated the value of clickstream data in modeling student behaviors that correlate with their learning outcomes (Agudo-Peregrina et al., 2014, Baker et al., 2020, Cohen, 2017, Crossley et al., 2016, Macfadyen and Dawson, 2010, You, 2016).
We introduce a novel model, Wide & Deep Item Response Theory (IRT), designed to predict a student’s post-test performance. Wide & Deep IRT combines the strengths of traditional IRT models with the flexible ‘Wide & Deep Learning for Recommender Systems’ (Cheng et al., 2016). The IRT component of the model enables accurate estimation of students’ abilities, while the deep learning component effectively utilizes clickstream data. This model has demonstrated its proficiency by placing second on the public leaderboard and third on the private leaderboard of the EDM Cup 2023 competition.
In addition to providing accurate predictions of post-test question correctness, our model offers valuable insights into behavioral patterns across different ability groups. This allows us to gain a deeper understanding of behaviors that may contribute to suboptimal learning outcomes. Specifically, with the Wide & Deep IRT model, students in the lowest math ability group were four times more likely to immediately request answers to questions than students from other groups. Moreover, these students requested answers three times faster than their counterparts. Remarkably, in approximately 21.80% of instances, they requested an answer within 3 seconds after a question was presented to them. This rapid response time led us to suspect that these low-ability students might have been gaming the system. The brief duration suggests that they were not making a genuine effort to solve the problems.
Throughout the remainder of this manuscript, we use the terms ‘item’ and ‘question’ interchangeably to denote a question posed to a student on a learning platform. Similarly, ‘item response’ and ‘question answer’ are used interchangeably to indicate the response a student provided to a given question. We use the term ‘ability’ to denote a student’s proficiency in a specific skill. This term, frequently utilized within the realm of item response theory research, equates to the concepts of ‘knowledge state’ and ‘mastery of skills’ that are often used in knowledge tracing literature. We opt to use this single term consistently throughout the manuscript to enhance clarity and coherence.
2. Related Works
2.1. Knowledge Tracing
Knowledge tracing is a method frequently utilized in the field of intelligent tutoring systems to model a student’s evolving skills and ability over time. The approach stems from the work of Corbett and Anderson (1994) that aimed to model students’ evolving ability while learning to write short programs. Their work introduced Bayesian Knowledge Tracing (BKT), in which a student’s knowledge state or ability for each skill is binary: either learned or unlearned. BKT assumes that a student will correctly respond to a question if they have mastered the relevant skill and do not make a mistake (slip) while responding, or if they happen to guess the answer correctly by chance. Pardos and Heffernan (2011) attempted to improve BKT’s predictive accuracy by incorporating item difficulty into the model. They proposed that this could be achieved by fitting item-specific guessing and slipping rates. The authors found that BKT with item difficulty performed better than the original model, but only with certain datasets. Similarly, Yudelson et al. (2013) attempted to enhance BKT by adding student-specific parameters. The original BKT assumed every student had the same initial ability and learning rate. The authors explored individualizing these parameters and found that a student-specific learning rate fit the data considerably better, while student-specific initial ability provides only marginal improvement.
Knowledge tracing models have evolved significantly since the introduction of BKT. The work of Piech et al. (2015) on Deep Knowledge Tracing (DKT) is arguably one of the most important landmarks in this progress. Rather than explicitly assuming how a student’s ability evolves over time and how each skill influences their question-answering accuracy, the authors framed this as a pure sequential prediction problem. They applied Long Short-Term Memory (LSTM) (Hochreiter and Schmidhuber, 1997) to data to learn how a student’s ability evolves over time and how this impacts their question-answering performance. The authors found that the DKT model significantly outperformed BKT across a range of public datasets. This progress sparked extensive research on using deep learning models to improve knowledge tracing. Yeung and Yeung (2018) discovered an inconsistency in DKT where the model’s estimates of a student’s skill could decrease despite the student excelling in the skill. To address this, they introduced a regularized DKT to ensure consistent estimation. Zhang et al. (2017) proposed the use of an autoencoder (Hinton and Salakhutdinov, 2006) to compress question-level features into a dense vector, which is then used as input to the DKT models. Zhang et al. (2017) introduced Dynamic Key-Value Memory Networks (DKVMN), which employed a modified memory augmented neural network (MANN) (Graves et al., 2016) to replace the LSTM cell in DKT. Unlike LSTM, which compresses a student’s ability across all skills into a single vector, MANN uses a matrix to more effectively represent a student’s ability. Each vector within the matrix represents the ability associated with a specific skill.
Recent developments in knowledge tracing models exhibit two significant trends. The first trend is the shift from an RNN-based approach to an approach based purely on attention (Vaswani et al., 2017). In this line of research (Choi et al., 2020, Pandey and Karypis, 2019, Pandey and Srivastava, 2020, Pu et al., 2020, Ghosh et al., 2020, Pu et al., 2021, Shin et al., 2021), a student’s abilities are not compressed into a vector until the inference stage. That is, these models calculate students’ abilities only when predicting response correctness based on their past performance on similar questions. The similarity between historical and target questions is captured through the attention mechanism. The second trend aims to improve the representation of questions. This can be achieved by either learning the embedding of a question from its text (Liu et al., 2021, Tong et al., 2020), or the relationship between the underlying skills targeted by the question (Liu et al., 2020, Nakagawa et al., 2019, Song et al., 2022).
Knowledge tracing is the prevailing method for estimating students’ abilities in intelligent tutoring systems. Therefore, we include knowledge tracing models as baselines for the Wide & Deep IRT model. However, since knowledge tracing is primarily designed to predict the correctness of a student’s answer to the next question, we propose a straightforward approach that uses knowledge tracing models to predict the correctness of students’ post-test questions in the experimental section.
2.2. Item Response Theory
Item Response Theory (IRT) is a widely used psychometric framework in educational and psychological research for analyzing test item responses. IRT is based on the idea that test items have varying levels of difficulty and discrimination, while individuals possess different levels of latent traits. IRT estimates the parameters for each item within a scale, allowing differentiation between a person’s response to the item and their underlying level of the latent traits (or ability) being measured (Hambleton et al., 1991). In contrast, Classical Test Theory requires contextual interpretation that considers characteristics of both the test and test-takers.
IRT models estimate several measurement properties for both items and respondents. The latent trait, \(\theta _i\), represents a respondent’s ability, which is a theoretical construct that cannot be directly observed or measured, but is inferred from their pattern of responses to the test items. Item difficulty, \(b_j\), refers to the point on the latent trait continuum where the probability of a correct response is 50%. Higher difficulty indicates greater challenge and requires a higher level of ability to provide a correct response. Item discrimination, \(a_j\), refers to the ability of an item to distinguish individuals with varying levels of the latent trait being measured. Items with more discrimination parameters are more informative and can effectively differentiate individuals with varying levels of the latent construct. In IRT models, each individual’s response to an item is influenced by their \(\theta _i\) value and the item parameters, such as item difficulty and discrimination.
IRT models have evolved with variants based on the number of parameters estimated. The one-parameter logistic (1-PL) IRT model (Rasch, 1961), also known as the Rasch model, assumes constant item discrimination and estimates item difficulty. The 2-PL model (Lord, 1952, Birnbaum, 1968) estimates both item difficulty and discrimination. The 3-PL model (Lord, 1980) extends the 2-PL model by incorporating a guessing parameter, \(c_i\), to account for the probability of guessing correct responses when the latent trait is low. This parameter is particularly useful for multiple-choice items, where individuals have a probability of guessing the correct answer. Finally, the 4-PL model introduces an upper asymptote parameter, \(d_i\), to capture the probability of slipping even at very high trait levels (Baker and Kim, 2004, Embretson and Reise, 2013).
IRT models provide a powerful framework for understanding the relationship between item responses and latent traits in various domains. In educational assessment, IRT is utilized for test development and calibration, and to identify problematic items (Embretson and Reise, 2013, Baker, 2001). It is also valuable in computerized adaptive testing, where item difficulty is dynamically adjusted based on estimated trait levels, leading to more precise assessments (Linden et al., 2000). In psychology, IRT aids in constructing reliable scales and assessing latent traits (Embretson and Reise, 2013). IRT is also employed in health sciences to develop patient-reported outcome measures (PROMs) and health-related quality of life assessments (Cella et al., 2010, Jefford et al., 2017).
With recent advancements in deep learning and artificial intelligence, researchers have explored the integration of IRT principles within deep learning models, which exhibit superior performance. Cheng et al. (2019) proposed Deep Item Response Theory (DIRT), which involves using a proficiency vector to represent student proficiency and dense embedding to represent question texts and knowledge concepts. They used the item response function to predict student performance, and their experimental results on real-world data demonstrate the effectiveness and interpretability of DIRT. Tsutsumi et al. (2021b) introduced Deep-IRT, which does not assume that abilities are randomly sampled from a normal distribution. Their study showed that Deep-IRT provides more accurate estimates of individuals’ abilities compared to conventional IRT models.
Yeung (2019) proposed integrating IRT models with DKVMN (Zhang et al., 2017) to predict the correctness of students’ answers to the next question. This approach retains the prediction power of DKVMN while benefiting from the interpretability of IRT. Tsutsumi et al. (2021a) further improved this integration by introducing two independent networks: a student network and an item network. Their results show improved prediction power of DKVMN while preserving the interpretability of IRT.
In this paper, we present a new approach in alignment with the ongoing trend of merging IRT with deep learning models. Our aim is to augment the widely-used ‘Wide & Deep Learning for Recommender Systems’ (Cheng et al., 2016). The author of the original model argued that deep neural networks can effectively capture complex feature interactions and generalize to unseen feature combinations through dense embeddings for sparse features. However, these networks may overgeneralize when dealing with high-dimensional sparse features that exhibit rare co-occurrences in the data. To address this challenge, the model uses the output of the deep neural network as an input to a generalized linear model. This generalized linear model is the ‘wide component’ and the deep neural network is the ‘deep component.’
‘Wide & Deep Learning for Recommender Systems’ serves as a suitable base model for several reasons. First, it maintains substantial traction within the field of recommender systems research. Second, it can process any input feature. Lastly, it can address the challenge posed by sparse student-item interactions when predicting students’ responses to future items.
In our approach, we integrate ’Wide & Deep Learning for Recommender Systems’ with IRT through two key modifications. Initially, we transition the wide component into a conventional IRT model, incorporating item difficulty parameters (\(\beta _j\)) and guessing parameters (\(c_j\)) as sparse features. Subsequently, we apply the deep component to each user-item response and compute the mean of all deep component outputs to estimate a student’s ability (\(\theta _i\)). Detailed insights into our model can be found in section 4. Through empirical evaluations conducted on the real-world dataset, EDM Cup 2023, we demonstrate that our approach not only enhances the performance of conventional IRT models, but also preserves their interpretability.
3. Data
The dataset used in this study is from the EDM Cup 2023 competition2 hosted on Kaggle. This dataset is a byproduct of K-12 students engaging with the ASISSTments3 learning platform for their mathematics schoolwork and examinations. As illustrated in Figure 1, the mathematics curriculum on ASISSTments is divided into discrete units, each encompassing a set of closely interconnected mathematical topics. As part of the pedagogical process within each unit, teachers assign homework to students, referred to as ‘in-unit assignments’ in the dataset. Upon completion of a unit, teachers assess students’ comprehension and acquisition of unit skills through ‘unit test assignments.’ Our goal is to develop an accurate prediction model capable of predicting whether a student can correctly respond to each item in the unit test assignments based on their performance in the corresponding in-unit assignments.

The clickstream data recorded by the ASISSTments platform as students engaged with the in-unit assignments are included in the EDM Cup 2023 dataset. This clickstream data primarily comprises timestamped actions. Table 1 presents a comprehensive breakdown of the actions, highlighting those most pertinent to the learning activities. Beyond clickstream data, the dataset maps students’ test assignments to the corresponding in-unit assignments, and provides detailed information about each item as well as comprehensive metadata about the assignments.
| Action | % in all actions |
|---|---|
| correct response | 61.14% |
| wrong response | 26.93% |
| answer requested | 10.29% |
| hint requested | 1.25% |
| explanation requested | 0.36% |
| skill related video requested | 0.02% |
| live tutor requested | <0.01% |
Table 2 provides descriptive statistics for the dataset, which includes 34,652 students, 607,236 in-unit assignments and 53,615 test assignments. The in-unit assignments contain a total of 57,235 distinct items, while the unit test assignments contain another 1835 items. There are no overlapping items between in-unit assignments and unit test assignments. Clickstream data are provided for in-unit assignments, but not for unit test assignments. Therefore, when predicting whether a student will correctly answer an item in the unit test assignments, we use only the clickstream data from the corresponding in-unit assignments as input features.
| Statistics | In-Unit Assignments | Unit Test Assignments (With Item Scores) | Unit Test Assignments (No Item Scores) |
|---|---|---|---|
| # of students | 34,652 | 27,224 | 7,761 |
| # of assignments | 607,236 | 42,343 | 11,272 |
| # of items | 57,235 | 1,835 | 1,471 |
| # of item responses | 5,634,383 | 452,439 | 124,455 |
| # of actions | 22,924,203 | NA | NA |
| % correct | 67.51% | 58.55% | NA |
The assignments in the dataset are classified into three distinct categories: in-unit assignments, test assignments with item scores, and test assignments without item scores. The test assignments with item scores were provided by the competition host to train models during the competition. Test assignments without item scores were used by the competition host to score models on the public and private leaderboards. Table 2 presents the statistics of each category of assignments. Our predictive model employs the in-unit assignments as input and trains and learns its parameters using the test assignments with item scores. The test assignments without item scores are used for model evaluation. We used the Kaggle competition leaderboard to retrieve model performance without gaining access to the item scores in the test assignments.
4. Feature Engineering
This section describes the features used as inputs for the Wide & Deep IRT model. These features, extracted from students’ in-unit assignments item responses, have been validated by existing literature for their applicability and effectiveness in education contexts.
| Action Sequence | % in all Action Sequences | Cumulative % |
|---|---|---|
| correct response | 67.51% | 67.51% |
| wrong response, correct response | 9.61% | 77.12% |
| answer requested, correct response | 5.94% | 83.06% |
| wrong response, answer requested, correct response | 4.55% | 87.61% |
| wrong response\(\times \)2, answer requested, correct response | 2.48% | 90.09% |
| wrong response\(\times \)2, correct response | 2.34% | 92.43% |
| wrong response\(\times \)3, answer requested, correct response | 1.87% | 94.30% |
| wrong response\(\times \)3, correct response | 0.61% | 94.92% |
| wrong response | 0.50% | 95.42% |
| help requested, correct response | 0.37% | 95.79% |
| Others | 4.21% | 100% |
4.1. Clickstream Data: Student Actions
Clickstream data provide valuable information on students’ learning behaviors. Previous studies have used clickstream data to reveal various behavioral patterns, including gaming the system (Baker et al., 2008), engagement and procrastination (Agudo-Peregrina et al., 2014, Lim, 2016, Park et al., 2018, You, 2016), and the use of trial-and-error approaches (Juhaňák et al., 2019). In this study, we focus on a subset of clickstream data produced while students responded to items on in-unit assignments. Each piece of clickstream data represents an action pertinent to learning or assessment, recorded as students responded to the items. Table 1 catalogs all actions employed by the model, along with their prevalence in the dataset. Actions associated with requests for assistance, namely ‘hint requested,’ ‘explanation requested,’ ‘skill-related video requested,’ and ‘live tutor requested,’ are relatively rare and conceptually similar. Therefore, they are grouped together as a single action cluster labeled ‘help requested.’ It is important to note that ‘answer requested’ is excluded from this cluster, as it signifies the student’s decision to abandon solving the problem rather than seeking to simplify it. Different methods of encoding a student’s action sequence were explored in this study, and detailed descriptions are provided below.
4.1.1. One-hot Encoding of Action Sequence
We arranged students’ actions while answering a particular item chronologically, thereby generating an action sequence. As shown in Table 3, 67.51% of the time, students correctly responded to an item on the first attempt, and 9.61% of the time, they figured out the answer after one failure. Interestingly, the ten most common action sequences account for 95.79% of all action sequences identified in our dataset. Given this skewed distribution, we applied one-hot encoding specifically to these ten predominant sequences, converting each into a unique binary vector where only a single bit is ‘on’ (or 1) and the rest are ‘off’ (or 0). Each unique vector represents one particular action sequence.
We consolidate less frequent action sequences outside the top ten into a single category labeled ‘other.’ This approach allowed us to focus on the most prevalent action sequences while acknowledging the presence and potential impact of the less frequent ones. By doing so, we ensured a comprehensive yet manageable representation of students’ action sequence data in our study.
4.1.2. Bag of Words and Term Frequency-Inverse Document Frequency
While one-hot encoding provides a way to engineer an action sequence as a feature, it has limitations when dealing with infrequent action sequences, as they are coded as ‘other.’ This approach may result in the loss of potentially valuable data. Alternatively, assuming that the order of actions within an item may have limited informational value, we used Bag of Words (BoW) in conjunction with Term Frequency-Inverse Document Frequency (TF-IDF) features to extract insights from student action data.
BoW is a popular text representation method in natural language processing that disregards the order of words when creating a vector representation. In the vanilla BoW, each entry of the text vector represents the frequency of a word in the text for all words in a corpus (a collection of texts). Alternatively, TF-IDF features are often used to capture not only word frequency in the text, but also the rarity of individual words in the corpus.
Just as text is a sequence of words, a student’s action sequence is a sequence of actions. Given that there are only seven types of actions in the data (as shown in Table 1), we can represent a student’s action sequence as a seven-dimensional vector. Each entry in the vector represents the TF-IDF feature for that action.
The TF-IDF feature has two components: term frequency and inverse-document frequency. The term frequency component is computed as follows:
\[tf_{td} = \frac {f_{td}}{\sum _{t' \in d}{f_{t'd}}}\]
The term frequency, denoted as \(tf_{td}\), represents the frequency of a specific term or word, \(f_{td}\), within a document, and this value is normalized by the document’s length, given by \(\sum {f_{t'd}}\). By considering each action as a ‘term’ and the collection of actions a student performs when responding to an item as a ‘document’, \(tf_{td}\) effectively quantifies the frequency of a particular action a student executes for an item, scaled by the total number of actions.
\[idf_{t} = log(\frac {N}{1 + n_t})\]
Inverse document frequency, \(idf_t\), gauges the prevalence of a term across all documents. Here, \(N\) denotes the total number of documents in the dataset, while \(n_t\) represents the number of documents containing the term \(t\). When applied to student actions, each sequence of student actions is treated as a unique ‘document’. Consequently, \(N\) becomes the overall quantity of student action sequences, and \(n_t\) represents the count of action sequences incorporating a specific action. Therefore, \(idf_t\) quantifies the relative prevalence of an action across all student item action sequences.
\[tf\mbox {-} idf_{td} = tf_{td} * idf_d\]
Finally, the TF-IDF score is obtained by multiplying \(tf_{td}\) and \(idf_t\). A student action has a high TF-IDF score if the action is infrequently observed across all student action sequences, yet recurrent within the specific action sequence under consideration.
4.1.3. Recurrent Neural Network encoding of action sequence
Recurrent neural networks (RNNs) have wide-ranging applications in handling sequential data, including sentiment analysis (Dong et al., 2014), knowledge tracing (Piech et al., 2015), translation (Sutskever et al., 2014), acoustic modeling (Sak et al., 2014), and various other domains. In this study, we employ Long Short-Term Memory (LSTM), a specific variant of RNN, to encode student action sequences. The choice of LSTM stems from its ability to capture long-term dependencies in the input sequences effectively.
We analyzed the dataset to determine an appropriate length for the action sequences. Based on our findings, we set the maximum action sequence length to eight, as a significant majority (99.71%) of the action sequences fell within this range. When an action sequence exceeded this predetermined threshold, we truncated the sequence by removing excess actions from the beginning of the sequence. When the length of an action sequence was less than eight, we appended a special ‘padding’ action to the left of the sequence until it reached the predetermined threshold. This step ensured that all sequences considered in the analysis adhered to the defined length criterion, thus maintaining consistency throughout the analysis. For example, to use LSTM to encode the action sequence: ‘wrong response, answer requested, correct response’, we first transformed each action into a dense vector using an embedding layer, the weights of which were learned during the training process. Since the action sequence had less than eight actions, we added five padding actions to the left. Subsequently, the padding action vectors and each action-embedded vector were inputted into the LSTM cell. The last output of the LSTM cell was then utilized as the embedding for the entire action sequence.
Although padding on the left side of a sequence causes the LSTM to have a different state when the first action takes place, empirical studies have shown that it performs better than adding padding tokens to the right side of a sequence (Dwarampudi and Reddy, 2019). In our experiment, we also found that padding on the left side slightly outperforms padding on the right side.
4.2. Item BERT Embedding
Bidirectional Encoder Representations from Transformers (BERT), developed by Google in 2018, is a language representation model that employs multiple layers of bidirectional transformer encoders (Devlin et al., 2019). The BERT model is pre-trained on two main tasks: predicting masked words using the surrounding context and predicting whether sentence A immediately follows sentence B. When applied to a new task, BERT undergoes a fine-tuning phase where the model is trained on task-specific inputs and outputs.
Previous research has demonstrated that a fine-tuned BERT model excels in a plethora of natural language processing tasks, including text classification (Sun et al., 2019), question answering (Qu et al., 2019), and sentiment analysis (Hoang et al., 2019), among others. In the field of education, fine-tuned BERT has shown promise in predicting the difficulty of multiple-choice items effectively (Benedetto et al., 2021), and pre-trained BERT features have been found useful in automating essay scoring (Beseiso and Alzahrani, 2020). However, a separate study revealed that fine-tuned BERT did not outperform traditional methods in the context of essay scoring (Mayfield and Black, 2020).
In this study, while item text is not directly available in the data, a variant of the pre-trained BERT embedding for item text is provided. Specifically, the text of all items generates a set of BERT embeddings, from which the 32 principal components are extracted to capture the most important information.
The percentage of students successfully answering an item, herein referred to as ‘item success rate’, provides valuable insights into the difficulty level of an item. It allows the model to distinguish between successful responses to more complex tasks and to simpler ones, with the former indicating a higher level of ability. This measure has been instrumental in gauging the item difficulty parameter in conventional IRT models. Previous research in knowledge tracing has used it as a feature to enhance model efficacy (Zhang et al., 2020).
In this study, we define ‘item success rate’ as the proportion of students who can correctly answer the item on their initial attempt without any assistance. This definition aims to address the observation that an overwhelming majority of students provide correct answers to in-unit assignment items after several attempts or with some assistance (e.g., hints). If we were to use their eventual success rate as a measure of item success rate, it could underestimate the item’s difficulty. Furthermore, we excluded items categorized as ‘ungraded open response’ due to the lack of scoring data for these responses in the dataset.
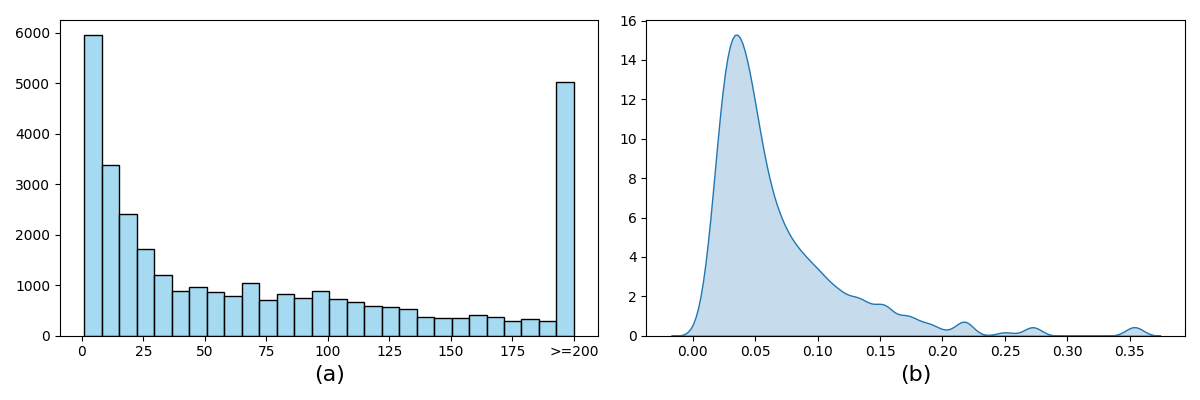
However, developing this feature presents challenges. A significant fraction of items (33.04%) was attempted by a maximum of only 20 students. Figure 2 (a) illustrates the frequency of attempts for items in the dataset. Items with fewer attempts tend to have less precise item success rate estimates compared to those with higher frequencies. To assess the precision of the item success rate, we assumed that every student had an independent and identical probability of correctly answering an item, thereby disregarding their mathematical aptitudes. Under this assumption, the item success rate follows an asymptotic normal distribution, in accordance with the Central Limit Theorem (Kwak and Kim, 2017). Specifically, the standard error of the item success rate is computed as \(\frac {s_j}{\sqrt {m_j}}\), where \(s_j\) represents the sample standard deviation for item \(j\) and \(m_j\) represents the number of times item \(j\) appears in the training data. Figure 2 (b) illustrates the distribution of the standard error of item success rate. For items with a standard error exceeding 0.125 4, we replaced the item success rate with the skill success rate.
4.3. In-Unit Assignment Item Success Rate
4.4. Assignment Recency
Previous studies (Khajah et al., 2016, Ghosh et al., 2020, González-Brenes et al., 2014) have empirically established the significant role that recency plays in predicting future item response success. Models such as BKT (Corbett and Anderson, 1994) show marked improvement when recency effects are factored in via the inclusion of forgetting parameters (Khajah et al., 2016). Similarly, attention-based knowledge tracing models see enhancements when information about the timing of response attempts is incorporated (Pu et al., 2020). It has thus become standard practice to employ mechanisms like RNNs or time and positional embeddings to address recency in knowledge tracing models.
Recency effects can influence learning outcomes through several channels. The first is through the process of forgetting, where previously acquired skills are lost over time, rendering distant item successes less relevant for predicting future success. The second is through the process of learning. It is plausible that a student, despite previous failures to provide a correct response to an item, has since mastered the requisite skills, a development reflected in correct response to recent items related to that skill. Consequently, recent items are a more reliable indicator of a student’s current ability than past items. The third channel, as identified by Khajah et al. (2016), is that the recency effect captures the impact of students’ time-varying engagement.
To integrate recency effects into the model, we introduce an ‘assignment recency’ feature, \(r_k\), representing the number of assignments between an in-unit assignment item \(k\) and a unit test item \(j\). For instance, if an in-unit assignment item \(k\) appeared in the last assignment prior to the unit test, then \(r_k = 0\). If item \(k\) appeared in the second to last assignment, \(r_k = 1\). This feature captures the recency of an in-unit assignment item \(k\) relative to a unit test item \(j\).
4.5. Missed Homework
A significant body of research in the fields of education and economics has investigated the association between homework and academic achievement. Cooper et al. (2006) conducted a comprehensive synthesis of studies from 1987 to 2003, revealing consistent evidence for a positive impact of homework on academic performance across various research design types (e.g., random experiments, multiple regression studies, and bivariate correlation). Recent studies have further expanded upon this finding by considering the nuanced effects of different homework characteristics. Keith et al. (2004) found that out-of-school homework had a substantial influence on course grades, while in-school homework did not exhibit the same effect. A more recent meta-analysis by Fan et al. (2017) specifically examined the relationship between homework and achievement in math and science, revealing an overall small yet positive association. Additionally, with the increasing prevalence of online homework platforms, studies have compared the effectiveness of online versus traditional homework. Magalhães et al. (2020) conducted a meta-analysis of 31 studies, indicating that while 15 studies showed no significant differences, nine studies reported better results with online homework, one study showed the opposite, and six studies reported mixed outcomes. These findings suggest that online homework is at least as effective as the traditional format in terms of student achievement.
Given the compelling empirical evidence regarding the effect of homework on grades, we believe that assigned but not attempted in-unit assignment items are valuable for predicting the correctness of students’ responses to unit test items. The occurrence of missing assignment items is quite common in the dataset, with 23.07% of assigned in-unit assignment items remaining unanswered by students.
5. Wide & Deep IRT
We formally describe the prediction problem here. We use \(x_{ik}\) to denote the item response features generated when student \(i\) responds to item \(k\) on the in-unit assignment. We use \(n_i\) to notate the number of in-unit assignment items student \(i\) answered. Thus, the sequence, \(x_{i0}, x_{i1}, ..., x_{in_i}\) represents all item response features student \(i\) generated while completing in-unit assignments.
We aim to infer if a student can correctly answer each unit test item, \(q_j\). We use \(y_{ij} \in \{0, 1\}\) to denote the correctness of the response provided by student \(i\) for unit test item \(j\). We aim to estimate the probability \(P(y_{ij} = 1 | x_{i0}, x_{i1}, ..., x_{in_i}, q_j)\). To tackle this problem, we propose a novel model, Wide & Deep IRT, which draws inspiration from both the success of IRT and the Wide & Deep model used in recommendation systems (Cheng et al., 2016). The Wide & Deep IRT model consists of two components: a wide component and a deep component.
5.1. Wide component
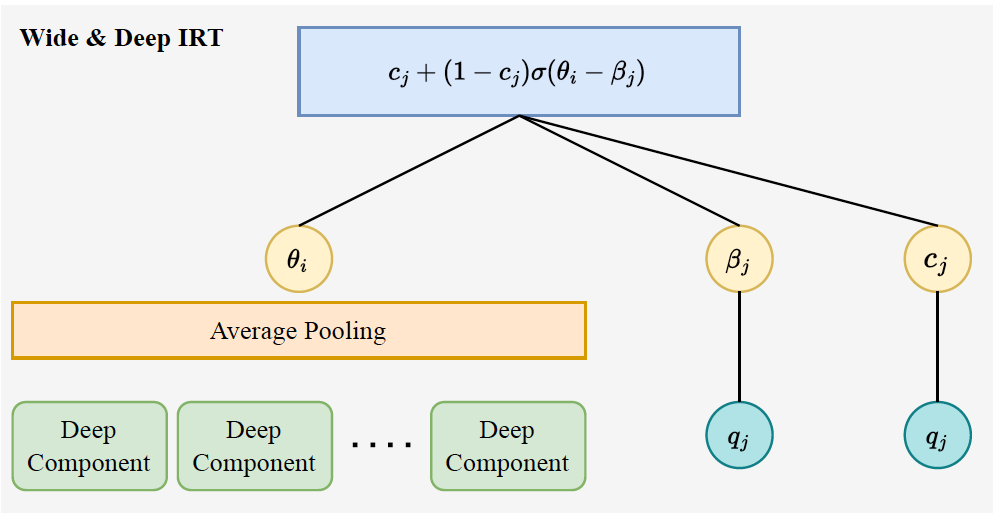
Figure 3 provides a visualization of the wide component, which is essentially a 1-PL IRT (Rasch) model with an optional guessing parameter for multiple-choice items. For a non-multiple-choice item:
\[p_{ij} = \frac {1}{1 + e^{- \theta _i + \beta _j}}\]
where \(p_{ij}\) is the probability that student \(i\) correctly answers item \(j\) on a unit test, \(\theta _i\) represents student \(i\)’s ability in related math concepts and \(\beta _j\) represents item \(j\)’s difficulty.
If item \(j\) is a multiple-choice item, we include a guessing parameter for each item:
\[p_{ij} = c_{j} + (1 - c_{j}) \frac {1}{1 + e^{- \theta _i + \beta _j}}\]
where \(c_i\) represents the probability of correctly guessing the answer of a multiple-choice item \(j\) from an average student.
To model a student’s ability, \(\theta _i\), we leverage a deep learning component. This is accomplished by leveraging features drawn from students’ actions during in-unit assignments and characteristics of the in-unit assignment items.
5.2. Deep component
The deep component leverages a suite of features described in section 4. These features include: the student’s action sequence, item BERT embedding, in-unit assignment item success rate, assignment recency, and missed homework. These features are derived from students’ in-unit assignment item responses to capture their mathematical ability.
\[\theta _i = f(x_{i0}, x_{i1}, ..., x_{in_i})\]
In the above formula, \(x_{ik}\) represents the item response features for student \(i\) and an in-unit assignment item \(k\). Details about item response features have been elaborated in the ‘Feature Engineering’ section. The function \(f\) is approximated via a three-layer neural network structured as follows:
\[h_{ik}^0 = ReLU(W_0x_{ik} + b_0)\] \[h_{ik}^1 = ReLU(W_1h_{ik}^0 + b_1)\] \[\theta _i = \frac {1}{n_{i}}(W_2h_{ik}^1 + b_2)\]
In these equations, \(W_*\) and \(b_*\) represent learned weights, \(h^*_{ik}\) denotes values in the corresponding hidden layer, and \(ReLU\) represents the rectified linear unit activation function (Nair and Hinton, 2010). Here, \(n_i\) indicates the number of in-unit assignment items student \(i\) attempted before answering the unit test items. Dropout layers (Srivastava et al., 2014) have been inserted between hidden layers to mitigate the potential risk of overfitting.
The model’s training process relies on the binary cross-entropy loss function, expressed as: \[\mathcal {L} = - \frac {1}{N} \sum y_{ij} \log (p_{ij}) + (1- y_{ij}) \log (1 - p_{t+1})\]
In this equation, \(y_{ij}\) is assigned a value of 1 if a student \(i\) answers a unit test item \(j\) correctly, and 0 otherwise.
6. Experiment
We compared the Wide & Deep IRT model, conventional IRT models, and deep knowledge tracing models using the EDM Cup 2023 dataset. Table 2 presents descriptive statistics for the data. We used unit test assignments without item scores along with their corresponding in-unit assignments as our testing data. We randomly selected 90% of the test assignments with item scores and their corresponding in-unit assignments as training data. The remaining 10% of unit test assignments with item scores and their corresponding in-unit assignments were used as validation data. This data division aligned with the setup of the EDM Cup 2023 competition, where the competition host evaluated models using unit test assignments without item scores on the public and private leaderboards. Consequently, we are able to calculate the leaderboard scores for all models.
In accordance with the competition setup, the unit test assignment serves as the sampling unit. This means that a unit test assignment is exclusively present in either the training or test data, but not in both. However, since students may have taken multiple unit test assignments, it is possible for students to appear in both training and test data. Overall, 333 students appear in both the training and test datasets. This dual presence has minimal impact on the final results, as less than 1% of all students are implicated. Furthermore, since we use in-unit assignments as model inputs and correctness of responses to unit test assignment items as outputs, there are no overlaps in inputs and outputs between the training, validation, and test data.
We used the training data to learn parameters for the models, the validation data for early stopping and hyperparameter tuning, and the test data for model evaluation. Consistent with the competition, we used area under the curve (AUC) as the evaluation metric. As the exact unit test items used to determine the public and private leaderboards were unknown, we relied on Kaggle submissions to calculate the AUC for the models. The Wide & Deep IRT was used in the competition, and its scores appear on the competition leaderboards 5. However, the baseline models were submitted after the competition, so those scores do not appear on the leaderboards.
6.1. Wide & Deep IRT
The Wide & Deep IRT model was implemented in Tensorflow (Abadi et al., 2016) and trained using the Adam optimizer (Kingma and Ba, 2015). The learning rate was set at 0.001, with a batch size of 1028. The model was trained for a maximum of 100 epochs, with early stopping employed if the validation loss did not improve for five consecutive epochs. The drop-out rate was adjusted from the set \(\{0.2, 0.4, 0.6\}\), while the hidden size \(h\) was varied from the set \(\{4, 8, 16, 32\}\).
The features of students’ in-unit assignment item responses were adjusted to a uniform length. We set the maximum length of the unit item response sequence to 200. We padded sequences shorter than 200 by adding zeroes to the left, and truncated sequences longer than 200.
6.2. Conventional IRT
Conventional IRT models only accommodate binary outcomes for an item response, implying that an answer can be classified only as correct or incorrect. However, a student’s response to an in-unit assignment item is typically characterized by a series of actions. To align these actions with the binary format required by conventional IRT models, we defined a response as correct if and only if a student correctly responded to an item on their first attempt without seeking assistance.
Conventional IRT models require a significant volume of responses to an item before they can yield precise estimates of item difficulty. An unreliable estimate of item difficulty can introduce inaccuracies when assessing a student’s mathematical competence. As illustrated in Figure 2 (a), a considerable proportion of in-unit assignment items had only been attempted by a handful of students. To address this issue, we excluded in-unit assignment items encountered too infrequently to provide reliable difficulty estimates. We tested a variety of thresholds for determining the rarity of an item, including 20, 40, and 60.
Conventional IRT estimates students’ abilities based on the correctness of their item responses. However, we lacked access to this data for unit test assignments. Therefore, we estimated the abilities of students in the testing set based on the correctness of their item responses to unit assignment, and did the same for the training and validation sets.
6.3. Deep Knowledge Tracing
Deep knowledge tracing models are primarily designed to predict the correctness of the response to the next item based on historical item responses, rather than inferring the correctness of post-test item responses. To overcome this limitation, we inserted 199 responses from in-unit assignment items to the left of each unit test assignment item, as if they were answered immediately prior to it. Deep knowledge tracing models were then trained to predict response correctness for the next item based on this sequence. However, during evaluation, we only used its predictions for unit test assignment items.
We chose Deep Knowledge Tracing (DKT) (Piech et al., 2015) and Context Aware Knowledge Tracing (AKT) (Ghosh et al., 2020) as our baseline knowledge tracing models. DKT is the first model to have employed deep learning in the knowledge tracing task. AKT is a recent model that incorporates attention and has achieved state-of-the-art outcomes in multiple public datasets.
Knowledge tracing models typically use the correctness of an item response as the primary input. Similar to the conventional IRT model, we define an item response as correct if a student answers it correctly on the first attempt without seeking assistance. These knowledge tracing models, which rely solely on the correctness of item responses from unit assignments, serve as our baseline models.
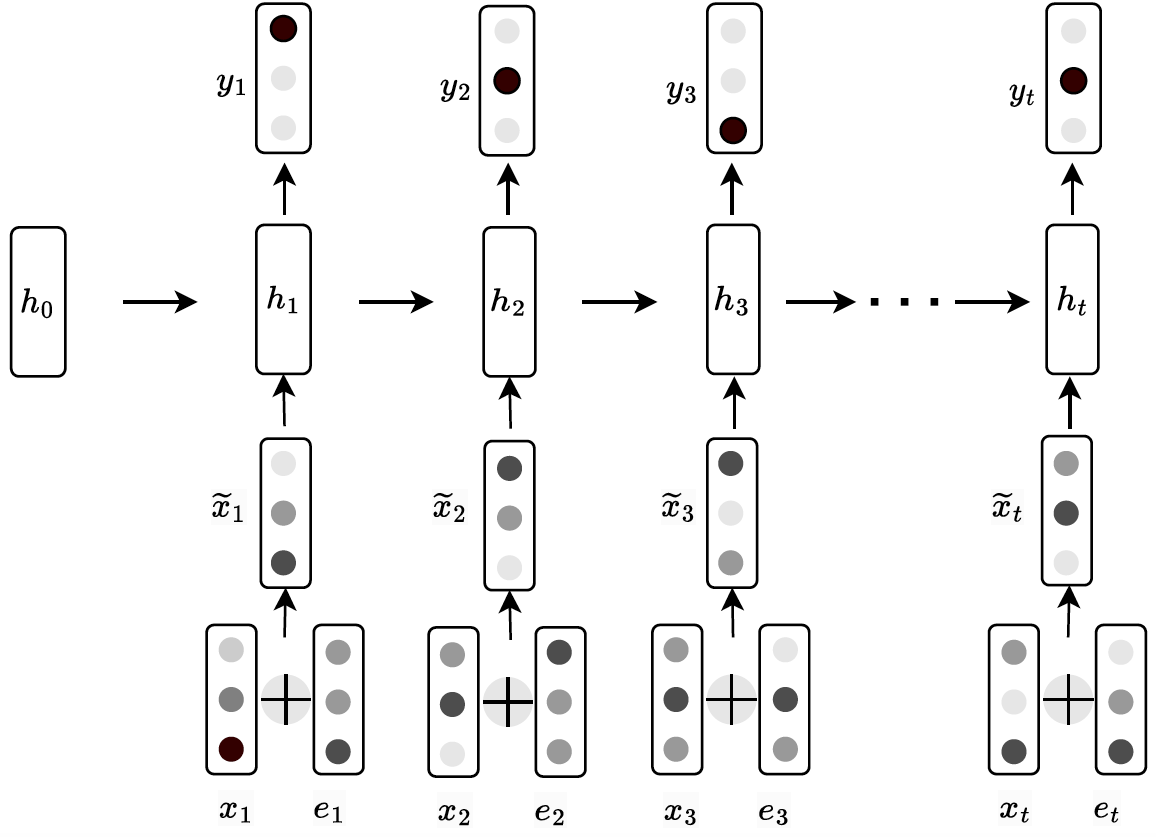
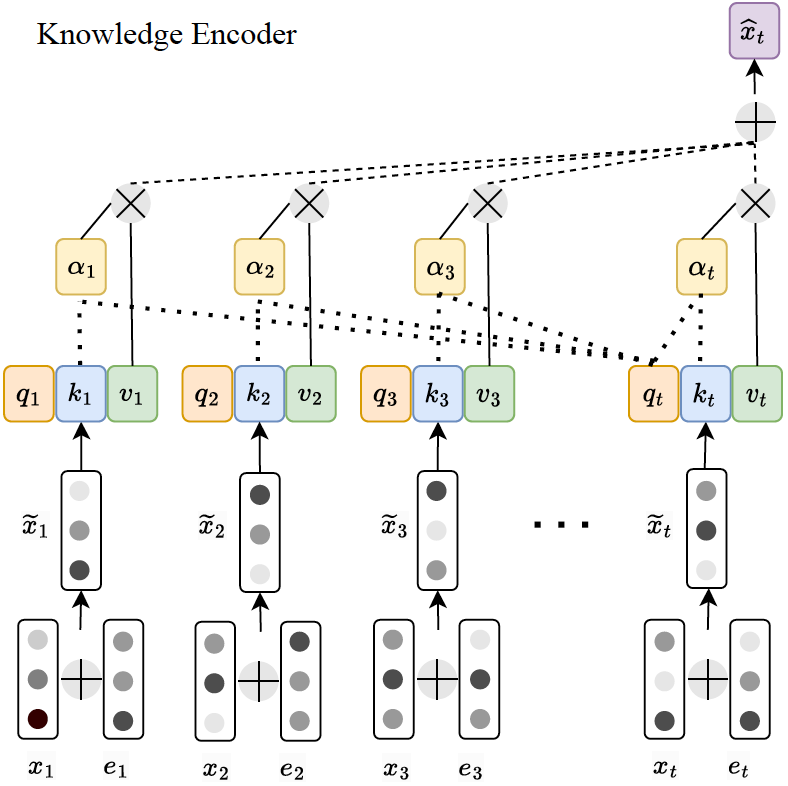
Additionally, to ensure a fair comparison between the Wide & Deep IRT and deep knowledge tracing models, we made simple adaptations to the knowledge tracing models to enable them to incorporate clickstream features for each item response. We employed a strategy akin to the one-hot encoding of action sequences used in Wide & Deep IRT: for each of the top 10 most frequent action sequences, we assigned an embedding vector \(e \in R^h\), where \(h\) is the hidden dimension configured for DKT and AKT. Both DKT and AKT have an input vector \(x_{j}\) that represents a student’s item response tuple \((q_j, c_j)\) where \(q_j\) is the \(j\)th question, and \(c_j\) is the correctness of the student’s response. We combined this input vector with the clickstream action sequence embedding and added it to the model. Specifically, DKT and AKT use \(\tilde {x}_j = x_j + e_j\) instead of \(x_j\) as the vector representing each student’s item response. Figure 4 illustrates the adaptation to DKT. Figure 5 shows the adaptation to the knowledge encoder of AKT.
Similar to Wide & Deep IRT, we trained both models for up to 100 epochs and used the validation dataset for early stopping. For DKT, we set the hidden state dimension to either 128 or 256. For AKT, we set the hidden state dimension to either 128 or 256 and the dropout rates to either 0.1 or 0.2. For the remaining hyperparameters, we used the default settings in the original authors’ code6.
7. Results
7.1. Model Performance
| Models | Test AUC public leaderboard | Test AUC private leaderboard |
|---|---|---|
| Rasch | 0.76348 | 0.76452 |
|
2-PL IRT | 0.76986 | 0.77314 |
| 3-PL IRT | 0.77239 | 0.77005 |
| DKT | 0.70129 | 0.66737 |
| DKT + Clickstream | 0.69757 | 0.66669 |
| AKT | 0.77659 | 0.76246 |
| AKT + Clickstream | 0.77578 | 0.76301 |
| Wide & Deep IRT | 0.79073 | 0.78625 |
Table 4 presents the models’ results on the test data. The Wide and Deep IRT model delivers the best performance across both test datasets. The three traditional IRT models and the AKT model yield slightly lower test AUCs, but they serve as robust baselines. However, DKT significantly underperforms the other models. A possible explanation is that DKT is the only model that operates at the skill level. Therefore, it cannot estimate the difficulty of a unit test item, which turns out to be crucial in determining a student’s item response correctness.
To our surprise, adding clickstream features to the DKT or AKT model does not significantly improve performance compared to the original versions of the models. One possible explanation is that deep knowledge tracing models are optimized to predict students’ immediate future performance, and the ways in which clickstream features influence short- and long-term performance may differ. Thus, knowledge tracing models might only capture the patterns of clickstream features relevant to short-term performance, which could differ from their impacts on students’ long-term performance. Meanwhile, since the Wide & Deep IRT model is trained to predict students’ long-term performance, it is able to accurately identify the patterns of clickstream features that affect students’ long-term performance.
Table 5 compares each model’s performance to other teams in the EDM Cup 2023 competition. The Wide & Deep IRT model outperforms the majority of other teams. Intriguingly, only a handful of teams, specifically 6 to 7, are able to surpass the test AUCs achieved by any of the conventional IRT models. For deep knowledge tracing models, AKT (with or without clickstream features) achieved a high ranking on the leaderboard, with only 5 teams achieving better scores for the public test data, and 6 teams achieving better scores for the private test data. However, DKT (with or without clickstream features) only achieved a mediocre ranking on the public leaderboard and proved to be one of the weaker models based on its score on the private leaderboard.
| Models | # of teams with better public leaderboard score | # of teams with better private leaderboard score |
|---|---|---|
| Rasch | 7 | 6 |
|
2-PL IRT | 6 | 6 |
| 3-PL IRT | 6 | 6 |
| DKT | 15 | 39 |
| DKT + Clickstream | 15 | 39 |
| AKT | 5 | 7 |
| AKT + Clickstream | 5 | 7 |
| Wide & Deep IRT | 1 | 2 |
| Removed Feature | Test AUC public leaderboard |
Test AUC private leaderboard | ||
|---|---|---|---|---|
| score | difference | score | difference | |
| click data: student actions | 0.73705 | -0.05368 | 0.74418 | -0.04207 |
| item BERT embedding | 0.79212 | +0.00139 | 0.78643 | +0.00018 |
| in unit item success rate | 0.78815 | -0.00258 | 0.78237 | -0.00388 |
| assignment recency | 0.78902 | -0.00171 | 0.78267 | -0.00358 |
| missed homework | 0.78945 | -0.00128 | 0.78184 | -0.00441 |
Table 6 examines the contribution of each feature to the model’s performance by removing the corresponding feature while retaining the others. It is evident that the student action sequence significantly influences model performance. Removing this feature results in a decrease in test AUC from 0.78073 to 0.73705 on the public leaderboard, and from 0.78625 to 0.74418 on the private leaderboard. The contributions of the in-unit assignment item success rate, assignment recency, and missed homework features are relatively marginal compared to the action sequence feature. Removing any one of these features leads to an average decrease in model performance by approximately 0.0019 and 0.0040 on the public and private leaderboards, respectively. Interestingly, removing the BERT embedding results in an increase in model performance, suggesting that the BERT embedding introduces only noise into the model. This could be due to the use of the principal components of the BERT embedding, which might result in the loss of some intrinsic information. Additionally, although previous research has highlighted the value of BERT embeddings in revealing item information, this typically involves fine-tuning the BERT model for the prediction task, rather than using the pre-trained embeddings. Unfortunately, due to a lack of item text data, we were unable to fine-tune the BERT model.
Table 7 further examines Wide & Deep IRT’s performance using different encoding strategies for student action sequences. The results show that different approaches yielded comparable results. The LSTM encoding performed well on the public leaderboard, while BoW with TF-IDF features dominated the private leaderboard. Interestingly, order-preserving encodings (i.e., one-hot encoding and LSTM) marginally outperform the order-agnostic approach (i.e., BoW) on the public leaderboard, but fell short on the private leaderboard. This suggests that the sequence order may have varying influence on different action sequences. Unfortunately, without knowing how the EDM Cup 2023 test data were divided between the public and private leaderboards, it remains unclear which action sequences are more affected by the order. Overall, all three encoding strategies are equally efficient on this dataset.
| Action Sequence Encoding Strategy | Test AUC public leaderboard | Test AUC private leaderboard |
|---|---|---|
| Onehot | 0.79073 | 0.78625 |
| BoW with TF-IDF | 0.78859 | 0.78699 |
| LSTM (state dimension = 8) | 0.79211 | 0.78578 |
In term of model size, Wide & Deep IRT requires the fewest parameters. The Wide & Deep IRT reported in Table 4 only requires approximately 5,200 parameters (the first hidden layer of the deep component comprises 16 dimensions, the second has 8 dimensions, and the final layer contains just one dimension). Despite their conceptual simplicity, conventional IRT models require learning a large number of item difficulty and student ability parameters. The parameter counts for a Rasch model ranges from 69.8 thousand to 77.4 thousand depending on the threshold used to exclude rare items appearing on unit assignments. This significant difference in parameter count arises because the Wide & Deep IRT model does not require a student parameter for each student, nor does it need to learn an item parameter for every item in the unit assignments. Deep knowledge tracing models involve a larger number of parameters. DKT and AKT reported in Table 4 have 1.1 million and 3.5 million parameters respectively. Similar to conventional IRT, deep knowledge tracing models need to learn embeddings for in-unit assignment items or associated skills. However, Wide & Deep IRT does not require this, resulting in significantly fewer parameters. When model performance is comparable, a lighter model is preferred due to faster training and deployment times.
7.2. Student behavior and math ability
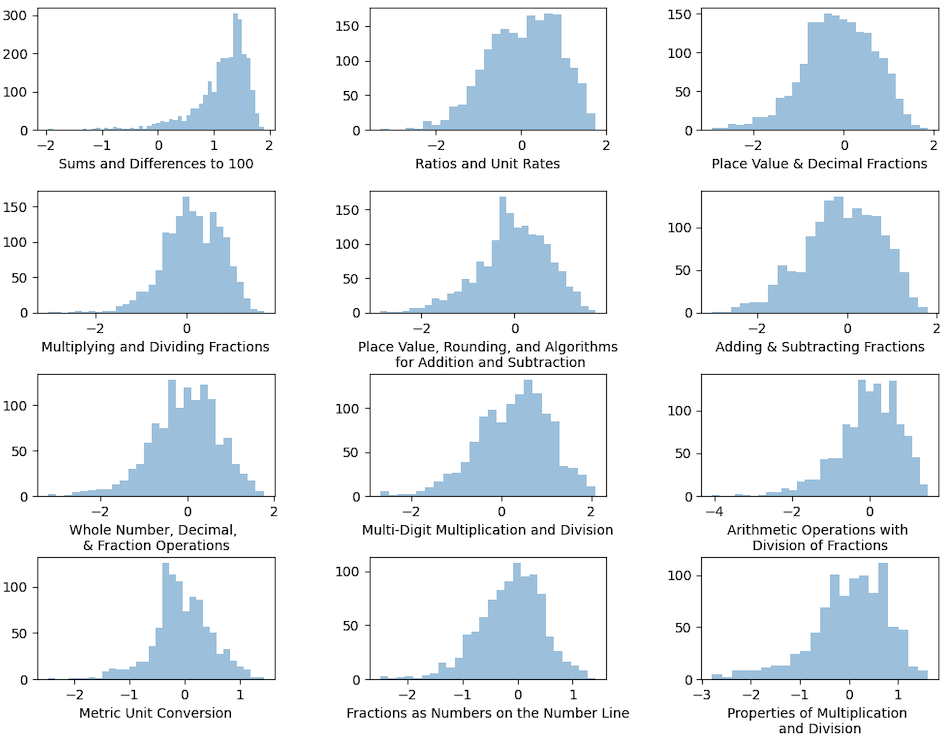
Wide & Deep IRT estimates students’ math ability for each unit, as shown in Figure 6, which displays the distribution of student mathematical abilities across the most frequently engaged units. Units in the ASSISTments framework typically align with one or more domains defined by the Common Core State Standards.7 To illustrate, the unit ‘Sums and Differences to 100’ corresponds to the domains ‘Number and Operations in Base Ten’ and ‘Operations and Algebraic Thinking’ for second-grade learners. This suggests that teachers could utilize this model to assess individual students’ math abilities, enabling them to provide personalized remediation plans for those who struggle with certain math units while performing well in others. Furthermore, teachers could apply this model to evaluate the overall math proficiency of their classes across various units and tailor their teaching plans accordingly. For instance, they might allocate additional time to units when a significant portion of the class is estimated to have lower math abilities, or they may need to reevaluate their teaching strategies for units when many students are facing difficulties.
Using the Wide & Deep IRT’s estimation of student math ability allows us to observe student behavior patterns across varying ability groups. Figure 7 visualizes the distribution of behaviors across these groups. Students are divided into five groups based on their math ability, each representing 20% of the total student population. Group zero consists of students in the lowest 20% of math ability, while group four includes those in the top 20%.
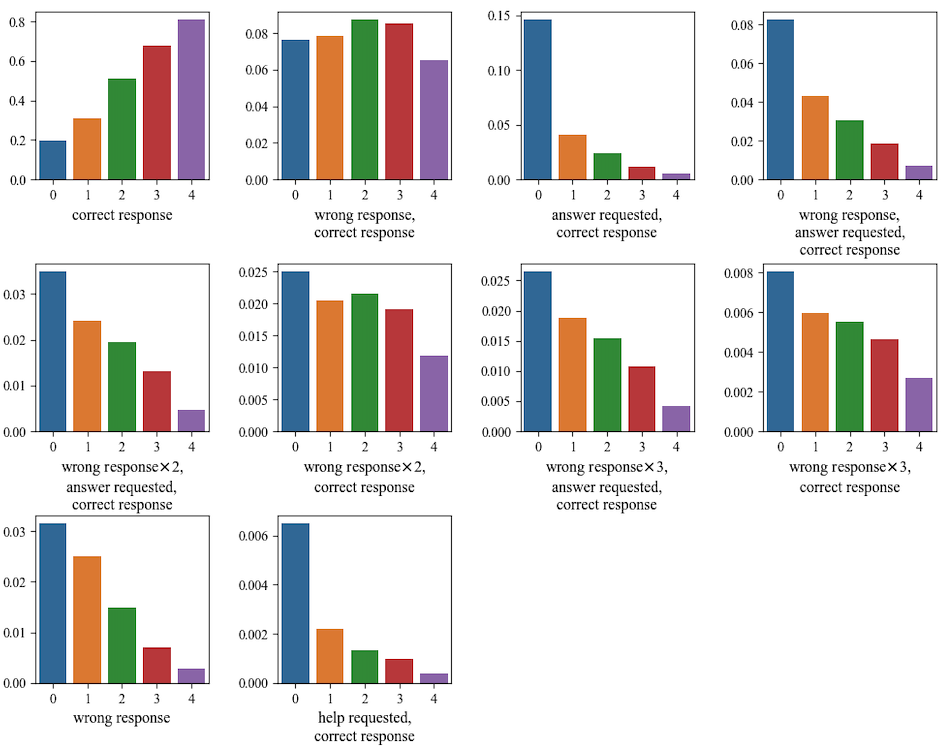
The y-axis denotes the likelihood of undertaking a specific action sequence when responding to an item. Each bar plot corresponds to a different action sequence, as defined in Table 3. For instance, the top left bar plot represents the ‘correct response’ action sequence, indicating that a student correctly answered an item on their first attempt without assistance.
This visualization reveals that students in group zero (lowest math ability) had roughly a 20% probability of answering an item correctly on their first attempt without assistance. As expected, this probability increases for students in higher ability groups. Specifically, for group four (the highest math ability), the likelihood reaches around 80%.
Remarkably, the bar plot in the first row and third column reveals that students in the lowest ability group were over four times more likely to engage in the ‘answer requested, correct response’ action sequence than any other group. This suggests that students with the lowest math ability are more inclined to request the answer to a question before even attempting to resolve the problem. The final bar plot illustrates that students in the lowest ability group were also over three times more likely to engage in the ‘help requested, correct response’ action sequence compared to students in other groups. This indicates their greater tendency to seek assistance before attempting to answer the question. Lastly, as shown in the final bar plot on the first row, students with the least math ability are more than twice as likely to request the answer following their initial failed attempt to answer the question compared to their peers in other groups.
While one interpretation could be that lower-ability students are gaming the system by quickly requesting answers and hints, it is also possible that these students are struggling with the questions and lack the necessary knowledge to answer them, prompting them to request answers or assistance before they attempt to respond. To investigate this issue further, we considered two additional metrics: how quickly lower-ability students requested help or the answer, and how likely they were to seek assistance for more challenging questions. If these students were indeed gaming the system, we would expect them to have requested answers immediately, even for questions that are relatively straightforward.
| Math ability groups | <3 seconds | <5 seconds | <10 seconds |
|---|---|---|---|
| Low | 21.80% | 39.44% | 56.17% |
| Below Average | 10.88% | 22.22% | 36.29% |
| Average | 9.69% | 20.20% | 33.02% |
| Above Average | 8.24% | 17.60% | 30.37% |
| High | 6.88% | 15.12% | 27.25% |
Table 8 provides a comparative analysis of the time interval between when students first saw the question and when they requested an answer prior to any attempts, across different ability groups. The students in the lowest math ability group tended to request answers more quickly. In extreme cases, approximately 21.80% of answer requests from this group occurred within just 3 seconds of students viewing the question. This raises concerns about whether they had adequate time to fully comprehend the question before requesting an answer, suggesting the possibility that they were strategically manipulating the system. Additionally, even when these students may have had enough time to comprehend the questions, they tended to give up and request answers significantly faster than their peers from other math ability groups.
Since Wide & Deep IRT does not estimate item difficulty parameters for in-unit assignment items, we utilized item success rate as a proxy for item difficulty. We divided items into five groups based on their success rate and computed the likelihood of a student directly requesting an answer upon encountering an item from a particular success rate group.
Figure 8 reveals the relationship between item success rate and the probability of requesting an answer without making an attempt across different math ability groups. Overall, as item difficulty decreases, so does the probability of students requesting the answer before attempting to respond. In addition, students in higher math ability groups are less likely to request answers before attempting to respond.
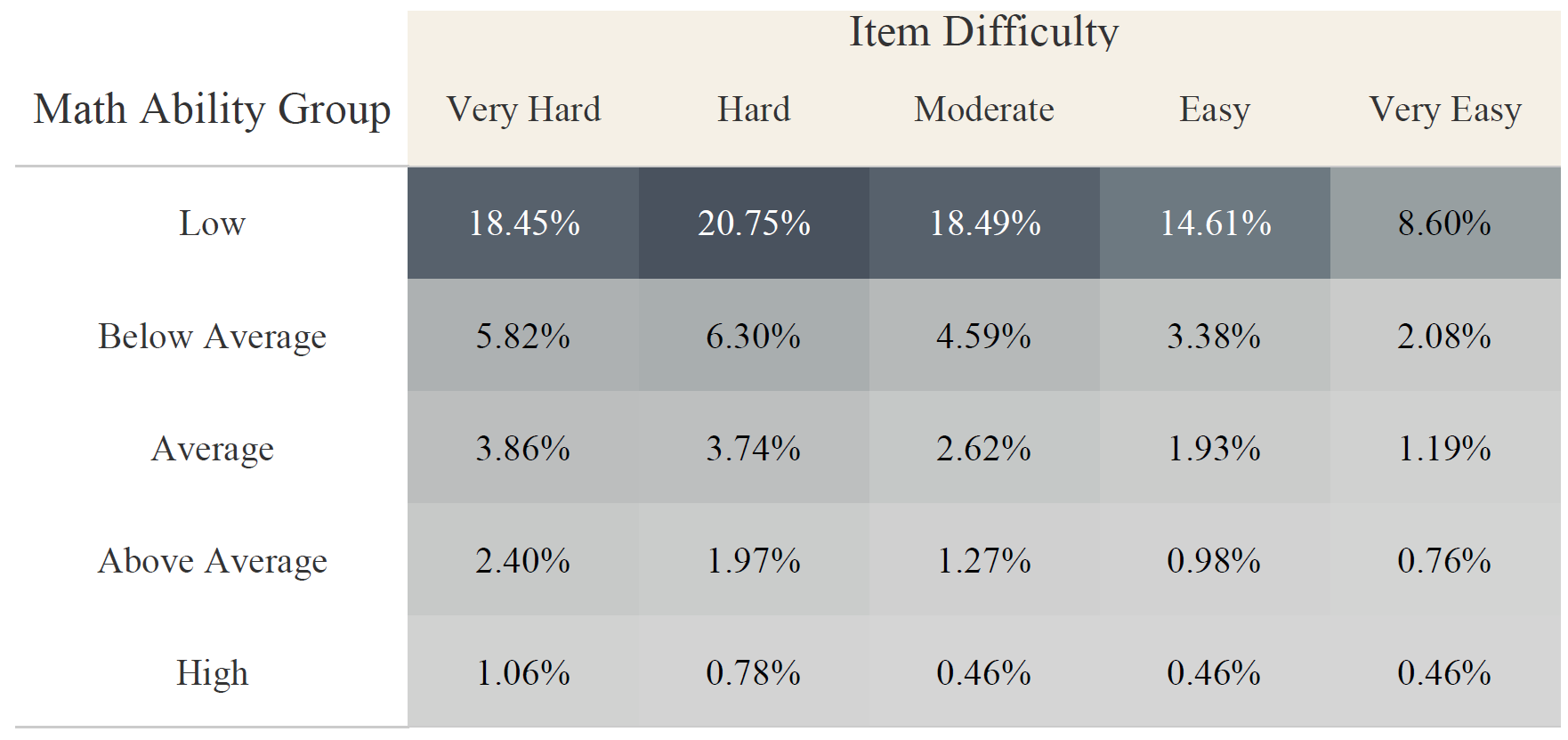
Interestingly, students in the lowest math ability group were less inclined to directly request answers when the questions were easier. Specifically, when presented with items from the easiest group, they only directly requested an answer in 8.60% of instances. However, when presented with items from the hardest group, their likelihood of directly requesting answers increased to 18.45% . This suggests that not all direct answer requests from students with the lowest abilities are attempts to game the system.
8. Discussion and Conclusions
In this study, we have introduced a novel model, Wide & Deep IRT, to predict a student’s performance on test assignments using information gathered from their in-unit assignments. We argue that this task offers a more relevant assessment of a student’s ability than traditional knowledge tracing tasks. Utilizing the public dataset from EDM Cup 2023, we have demonstrated that Wide & Deep IRT outperforms conventional IRT models and state-of-the-art deep knowledge tracing models when predicting correctness of responses to post-test questions. Moreover, Wide & Deep IRT placed second on the public leaderboard and third on the private leaderboard in the EDM Cup 2023 competition, indicating its competitiveness against models employed by other teams.
The Wide & Deep IRT model combines the strength of conventional IRT models and the ‘Wide & Deep Learning for Recommender Systems’ (Cheng et al., 2016). It not only estimates student ability, but also effectively utilizes complex features derived from clickstream data. Furthermore, our research demonstrates that this model serves as a valuable tool in exploring behavior patterns across different ability groups.
Our analysis has enabled us to identify potential indicators that could be used to detect attempts to game the system, such as directly requesting an answer to an easy question shortly after viewing it. These findings could have practical implications for enhancing the student learning experience. For instance, learning platforms could introduce countdown timers for easy questions, preventing students from requesting the answer before the timer expires. This strategy could nudge students towards solving problems themselves since the timer would require more time be spent on the item anyway.. Alternatively, the platform could encourage perseverance when students request answers too quickly, reminding them to take their time. Additionally, the system can offer progressive hints or prompts that guide students toward finding the solution. Gradually revealing hints can scaffold the problem-solving process and encourage students to think independently before seeking assistance. These interventions could foster a deeper learning experience and promote independent problem-solving skills.
The study has several limitations. Most importantly, while the Wide & Deep IRT framework offers flexibility to incorporate deep features at the item response level, it does not provide clear approaches for including individual-level features. For instance, although prior course grade is usually a strong predictor of future academic performance, it is not clear how to best integrate this individual-level feature into the model. Second, the work has only been evaluated using a single dataset, making it unclear how generalizable the findings are to other datasets. Finally, due to data limitations, our exploration was confined to the relationship between clickstream data and future grades within the same math unit. It remains to be seen whether students’ clickstream data across different math units exhibit distinct pattern that correspond with future grades.
In future studies, we plan to investigate how to incorporate individual-level features into the estimation of user ability within this framework. Additionally, the amount of time a student spends on each action could reveal more information beyond the mere sequence of actions they take. We intend to further explore the effect of time spent on each action on their future grades in upcoming studies.
References
- Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., Devin, M., Ghemawat, S., Irving, G., Isard, M., et al. 2016. Tensorflow: a system for large-scale machine learning. In 12th USENIX symposium on operating systems design and implementation (OSDI 16). USENIX Association, 265–283.
- Agudo-Peregrina, Á. F., Iglesias-Pradas, S., Conde-González, M. Á., and Hernández-García, Á. 2014. Can we predict success from log data in vles? classification of interactions for learning analytics and their relation with performance in vle-supported f2f and online learning. Computers in human behavior 31, 542–550.
- Baker, F. B. 2001. The basics of item response theory, 2nd ed. ERIC Clearinghouse on Assessment
and Evaluation. Retrieved from
https://eric.ed.gov/?id=ED458219. - Baker, F. B. and Kim, S.-H. 2004. Item response theory: Parameter estimation techniques, 2nd ed. Marcel Dekker, New York.
- Baker, R., Walonoski, J., Heffernan, N., Roll, I., Corbett, A., and Koedinger, K. 2008. Why students engage in “gaming the system” behavior in interactive learning environments. Journal of Interactive Learning Research 19, 2, 185–224.
- Baker, R., Xu, D., Park, J., Yu, R., Li, Q., Cung, B., Fischer, C., Rodriguez, F., Warschauer, M., and Smyth, P. 2020. The benefits and caveats of using clickstream data to understand student self-regulatory behaviors: opening the black box of learning processes. International Journal of Educational Technology in Higher Education 17, 1, 1–24.
- Benedetto, L., Aradelli, G., Cremonesi, P., Cappelli, A., Giussani, A., and Turrin, R. 2021. On the application of transformers for estimating the difficulty of multiple-choice questions from text. In Proceedings of the 16th Workshop on Innovative Use of NLP for Building Educational Applications, J. Burstein, A. Horbach, E. Kochmar, R. Laarmann-Quante, C. Leacock, N. Madnani, I. Pilán, H. Yannakoudakis, and T. Zesch, Eds. Association for Computational Linguistics, Online, 147–157.
- Beseiso, M. and Alzahrani, S. 2020. An empirical analysis of bert embedding for automated essay scoring. International Journal of Advanced Computer Science and Applications 11, 10, 204–210.
- Birnbaum, A. 1968. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores, F. M. Lord and M. R. Novick, Eds. Addison-Wesley, Reading, MA, 397–472.
- Cella, D., Riley, W., Stone, A., Rothrock, N., Reeve, B., Yount, S., Amtmann, D., Bode, R., Buysse, D., Choi, S., et al. 2010. The patient-reported outcomes measurement information system (promis) developed and tested its first wave of adult self-reported health outcome item banks: 2005–2008. Journal of clinical epidemiology 63, 11, 1179–1194.
- Cheng, H.-T., Koc, L., Harmsen, J., Shaked, T., Chandra, T., Aradhye, H., Anderson, G., Corrado, G., Chai, W., Ispir, M., Anil, R., Haque, Z., Hong, L., Jain, V., Liu, X., and Shah, H. 2016. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems. DLRS 2016. Association for Computing Machinery, New York, NY, USA, 7–10.
- Cheng, S., Liu, Q., Chen, E., Huang, Z., Huang, Z., Chen, Y., Ma, H., and Hu, G. 2019. Dirt: Deep learning enhanced item response theory for cognitive diagnosis. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management. CIKM ’19. Association for Computing Machinery, New York, NY, USA, 2397–2400.
- Choi, Y., Lee, Y., Cho, J., Baek, J., Kim, B., Cha, Y., Shin, D., Bae, C., and Heo, J. 2020. Towards an appropriate query, key, and value computation for knowledge tracing. In Proceedings of the Seventh ACM Conference on Learning @ Scale. L@S ’20. Association for Computing Machinery, New York, NY, USA, 341–344.
- Cohen, A. 2017. Analysis of student activity in web-supported courses as a tool for predicting dropout. Educational Technology Research and Development 65, 5, 1285–1304.
- Cooper, H., Robinson, J. C., and Patall, E. A. 2006. Does homework improve academic achievement? a synthesis of research, 1987–2003. Review of educational research 76, 1, 1–62.
- Corbett, A. T. and Anderson, J. R. 1994. Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction 4, 4, 253–278.
- Crossley, S., Paquette, L., Dascalu, M., McNamara, D. S., and Baker, R. S. 2016. Combining click-stream data with nlp tools to better understand mooc completion. In Proceedings of the Sixth International Conference on Learning Analytics & Knowledge. LAK ’16. Association for Computing Machinery, New York, NY, USA, 6–14.
- Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), J. Burstein, C. Doran, and T. Solorio, Eds. Association for Computational Linguistics, Minneapolis, Minnesota, 4171–4186.
- Dong, L., Wei, F., Tan, C., Tang, D., Zhou, M., and Xu, K. 2014. Adaptive recursive neural network for target-dependent Twitter sentiment classification. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), K. Toutanova and H. Wu, Eds. Association for Computational Linguistics, Baltimore, Maryland, 49–54.
- Dwarampudi, M. and Reddy, N. 2019. Effects of padding on lstms and cnns. arXiv preprint arXiv:1903.07288.
- Embretson, S. E. and Reise, S. P. 2013. Item response theory. Psychology Press, New York.
- Fan, H., Xu, J., Cai, Z., He, J., and Fan, X. 2017. Homework and students’ achievement in math and science: A 30-year meta-analysis, 1986–2015. Educational Research Review 20, 35–54.
- Ghosh, A., Heffernan, N., and Lan, A. S. 2020. Context-aware attentive knowledge tracing. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. KDD ’20. Association for Computing Machinery, New York, NY, USA, 2330–2339.
- González-Brenes, J., Huang, Y., and Brusilovsky, P. 2014. General features in knowledge tracing to model multiple subskills, temporal item response theory, and expert knowledge. In The 7th international conference on educational data mining, J. Stamper, Z. Pardos, M. Mavrikis, and B. M. McLaren, Eds. 84–91.
- Graves, A., Wayne, G., Reynolds, M., Harley, T., Danihelka, I., Grabska-Barwińska, A., Colmenarejo, S. G., Grefenstette, E., Ramalho, T., Agapiou, J., et al. 2016. Hybrid computing using a neural network with dynamic external memory. Nature 538, 7626, 471–476.
- Hambleton, R. K., Swaminathan, H., and Rogers, H. J. 1991. Fundamentals of item response theory. Vol. 2. SAGE.
- Hinton, G. E. and Salakhutdinov, R. R. 2006. Reducing the dimensionality of data with neural networks. Science 313, 5786, 504–507.
- Hoang, M., Bihorac, O. A., and Rouces, J. 2019. Aspect-based sentiment analysis using BERT. In Proceedings of the 22nd Nordic Conference on Computational Linguistics, M. Hartmann and B. Plank, Eds. Linköping University Electronic Press, Turku, Finland, 187–196.
- Hochreiter, S. and Schmidhuber, J. 1997. Long short-term memory. Neural computation 9, 8, 1735–1780.
- Jefford, M., Ward, A. C., Lisy, K., Lacey, K., Emery, J. D., Glaser, A. W., Cross, H., Krishnasamy, M., McLachlan, S.-A., and Bishop, J. 2017. Patient-reported outcomes in cancer survivors: a population-wide cross-sectional study. Supportive care in cancer : official journal of the Multinational Association of Supportive Care in Cancer 25, 10, 3171–3179.
- Juhaňák, L., Zounek, J., and Rohlíková, L. 2019. Using process mining to analyze students’ quiz-taking behavior patterns in a learning management system. Computers in Human Behavior 92, 496–506.
- Keith, T. Z., Diamond-Hallam, C., and Fine, J. G. 2004. Longitudinal effects of in-school and out-of-school homework on high school grades. School Psychology Quarterly 19, 3, 187.
- Khajah, M., Lindsey, R. V., and Mozer, M. C. 2016. How deep is knowledge tracing? In Proceedings of the 9th International Conference on Educational Data Mining, T. Barnes, M. Chi, and M. Feng, Eds. International Educational Data Mining Society, 94–101.
- Kingma, D. P. and Ba, J. 2015. Adam: A method for stochastic optimization. In International Conference on Learning Representations (ICLR). Ithaca, NY: ArXiv, 1–13.
- Kwak, S. G. and Kim, J. H. 2017. Central limit theorem: the cornerstone of modern statistics. Korean journal of anesthesiology 70, 2, 144–156.
- Lim, J. M. 2016. Predicting successful completion using student delay indicators in undergraduate self-paced online courses. Distance Education 37, 3, 317–332.
- Linden, W. J., van der Linden, W. J., and Glas, C. A. 2000. Computerized adaptive testing: Theory and practice. Springer.
- Lindsey, R. V., Shroyer, J. D., Pashler, H., and Mozer, M. C. 2014. Improving students’ long-term knowledge retention through personalized review. Psychological science 25, 3, 639–647.
- Liu, Q., Huang, Z., Yin, Y., Chen, E., Xiong, H., Su, Y., and Hu, G. 2021. Ekt: Exercise-aware knowledge tracing for student performance prediction. IEEE Transactions on Knowledge and Data Engineering 33, 1, 100–115.
- Liu, Y., Yang, Y., Chen, X., Shen, J., Zhang, H., and Yu, Y. 2020. Improving knowledge tracing via pre-training question embeddings. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, C. Bessiere, Ed. International Joint Conferences on Artificial Intelligence Organization, 1577–1583. Main track.
- Loh, H., Shin, D., Lee, S., Baek, J., Hwang, C., Lee, Y., Cha, Y., Kwon, S., Park, J., and Choi, Y. 2021. Recommendation for effective standardized exam preparation. In LAK21: 11th International Learning Analytics and Knowledge Conference. LAK21. Association for Computing Machinery, New York, NY, USA, 397–404.
- Lord, F. 1952. A theory of test scores. Psychometric Society.
- Lord, F. 1980. Applications of Item Response Theory To Practical Testing Problems, 1 ed. Lawrence Erlbaum Associates, New York.
- Macfadyen, L. P. and Dawson, S. 2010. Mining LMS data to develop an “early warning system” for educators: A proof of concept. Computers & Education 54, 2, 588–599.
- Magalhães, P., Ferreira, D., Cunha, J., and Rosário, P. 2020. Online vs traditional homework: A systematic review on the benefits to students’ performance. Computers & Education 152, 103869.
- Mayfield, E. and Black, A. W. 2020. Should you fine-tune BERT for automated essay scoring? In Proceedings of the Fifteenth Workshop on Innovative Use of NLP for Building Educational Applications, J. Burstein, E. Kochmar, C. Leacock, N. Madnani, I. Pilán, H. Yannakoudakis, and T. Zesch, Eds. Association for Computational Linguistics, Seattle, WA, USA → Online, 151–162.
- Nair, V. and Hinton, G. E. 2010. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning. ICML’10. Omnipress, Madison, WI, USA, 807–814.
- Nakagawa, H., Iwasawa, Y., and Matsuo, Y. 2019. Graph-based knowledge tracing: Modeling student proficiency using graph neural network. In 2019 IEEE/WIC/ACM International Conference on Web Intelligence (WI). IEEE Computer Society, Los Alamitos, CA, USA, 156–163.
- Pandey, S. and Karypis, G. 2019. A self attentive model for knowledge tracing. In Proceedings of The 12th International Conference on Educational Data Mining (EDM 2019), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. 384–389.
- Pandey, S. and Srivastava, J. 2020. RKT: Relation-aware self-attention for knowledge tracing. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management. CIKM ’20. Association for Computing Machinery, New York, NY, USA, 1205–1214.
- Pardos, Z. A. and Heffernan, N. T. 2011. KT-IDEM: Introducing item difficulty to the knowledge tracing model. In User Modeling, Adaption and Personalization:19th International Conference, UMAP 2011, Girona, Spain, July 11-15, 2011. Proceedings 19, J. A. Konstan, R. Conejo, J. L. Marzo, and N. Oliver, Eds. Springer, Berlin, Heidelberg, 243–254.
- Park, J., Yu, R., Rodriguez, F., Baker, R., Smyth, P., and Warschauer, M. 2018. Understanding student procrastination via mixture models. In Proceedings of the 11th International Conference on Educational Data Mining, K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society, 187–197.
- Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L., and Sohl-Dickstein, J. 2015. Deep knowledge tracing. In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 1. NIPS’15. MIT Press, Cambridge, MA, USA, 505–513.
- Pistilli, M. D. and Arnold, K. E. 2010. Purdue signals: Mining real-time academic data to enhance student success. About campus 15, 3, 22–24.
- Pu, S., Converse, G., and Huang, Y. 2021. Deep performance factors analysis for knowledge tracing. In Artificial Intelligence in Education, I. Roll, D. McNamara, S. Sosnovsky, R. Luckin, and V. Dimitrova, Eds. Springer International Publishing, Cham, 331–341.
- Pu, S., Yudelson, M., Ou, L., and Huang, Y. 2020. Deep knowledge tracing with transformers. In Artificial Intelligence in Education, I. I. Bittencourt, M. Cukurova, K. Muldner, R. Luckin, and E. Millán, Eds. Springer International Publishing, Cham, 252–256.
- Qu, C., Yang, L., Qiu, M., Croft, W. B., Zhang, Y., and Iyyer, M. 2019. BERT with history answer embedding for conversational question answering. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. SIGIR’19. Association for Computing Machinery, New York, NY, USA, 1133–1136.
- Rasch, G. 1961. On general laws and the meaning of measurement. In Proceedings of the IV Berkeley Symposium on Mathematical Statistics and Probability, J. Neyman, Ed. Vol. 4. University of California Press, Oakland, CA, USA, 321–333.
- Ritter, S., Yudelson, M., Fancsali, S. E., and Berman, S. R. 2016. How mastery learning works at scale. In Proceedings of the Third (2016) ACM Conference on Learning @ Scale. L@S ’16. Association for Computing Machinery, New York, NY, USA, 71–79.
- Sak, H., Senior, A. W., and Beaufays, F. 2014. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In 15th Annual Conference of the International Speech Communication Association, INTERSPEECH 2014, Singapore, September 14-18, 2014, H. Li, H. M. Meng, B. Ma, E. Chng, and L. Xie, Eds. ISCA, 338–342.
- Scruggs, R., Baker, R., and McLaren, B. 2020. Extending deep knowledge tracing: Inferring interpretable knowledge and predicting post-system performance. In Proceedings of the 28th International Conference on Computers in Education, H. J. S. et al., Ed. Australia: Asia-Pacific Society for Computers in Education.
- Scruggs, R., Baker, R. S., Pavlik, P. I., McLaren, B. M., and Liu, Z. 2023. How well do contemporary knowledge tracing algorithms predict the knowledge carried out of a digital learning game? Educational technology research and development 71, 3, 901–918.
- Settles, B. and Meeder, B. 2016. A trainable spaced repetition model for language learning. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), K. Erk and N. A. Smith, Eds. Association for Computational Linguistics, Berlin, Germany, 1848–1858.
- Shin, D., Shim, Y., Yu, H., Lee, S., Kim, B., and Choi, Y. 2021. Saint+: Integrating temporal features for ednet correctness prediction. In LAK21: 11th International Learning Analytics and Knowledge Conference. LAK21. Association for Computing Machinery, New York, NY, USA, 490–496.
- Song, X., Li, J., Lei, Q., Zhao, W., Chen, Y., and Mian, A. 2022. Bi-clkt: Bi-graph contrastive learning based knowledge tracing. Knowledge-Based Systems 241, 108274.
- Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. 2014. Dropout: a simple way to prevent neural networks from overfitting. The journal of machine learning research 15, 1, 1929–1958.
- Sun, C., Qiu, X., Xu, Y., and Huang, X. 2019. How to fine-tune bert for text classification? In Chinese Computational Linguistics, M. Sun, X. Huang, H. Ji, Z. Liu, and Y. Liu, Eds. Springer International Publishing, Cham, 194–206.
- Sutskever, I., Vinyals, O., and Le, Q. V. 2014. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems - Volume 2. NIPS’14. MIT Press, Cambridge, MA, USA, 3104–3112.
- Tong, H., Zhou, Y., and Wang, Z. 2020. Exercise hierarchical feature enhanced knowledge tracing. In Artificial Intelligence in Education, I. I. Bittencourt, M. Cukurova, K. Muldner, R. Luckin, and E. Millán, Eds. Springer International Publishing, Cham, 324–328.
- Tsutsumi, E., Kinoshita, R., and Ueno, M. 2021a. Deep-IRT with independent student and item networks. In Proceedings of the 14th International Conference on Educational Data Mining, I.-H. S. Hsiao, S. S. Sahebi, F. Bouchet, and J.-J. enn Vie, Eds. 510–517.
- Tsutsumi, E., Kinoshita, R., and Ueno, M. 2021b. Deep item response theory as a novel test theory based on deep learning. Electronics 10, 9, 1020.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., and Polosukhin, I. 2017. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems. NIPS’17. Curran Associates Inc., Red Hook, NY, USA, 6000–6010.
- Wise, S. L. 2017. Rapid-guessing behavior: Its identification, interpretation, and implications. Educational Measurement: Issues and Practice 36, 4, 52–61.
- Yeung, C.-K. 2019. Deep-irt: Make deep learning based knowledge tracing explainable using item response theory. In Proceedings of The 12th International Conference on Educational Data Mining (EDM 2019), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. 683–686.
- Yeung, C.-K. and Yeung, D.-Y. 2018. Addressing two problems in deep knowledge tracing via prediction-consistent regularization. In Proceedings of the Fifth Annual ACM Conference on Learning at Scale. L@S ’18. Association for Computing Machinery, New York, NY, USA, 1–10.
- You, J. W. 2016. Identifying significant indicators using lms data to predict course achievement in online learning. The Internet and Higher Education 29, 23–30.
- Yudelson, M. V., Koedinger, K. R., and Gordon, G. J. 2013. Individualized bayesian knowledge tracing models. In Artificial Intelligence in Education, H. C. Lane, K. Yacef, J. Mostow, and P. Pavlik, Eds. Springer Berlin Heidelberg, Berlin, Heidelberg, 171–180.
- Zhang, J., Shi, X., King, I., and Yeung, D.-Y. 2017. Dynamic key-value memory networks for knowledge tracing. In Proceedings of the 26th International Conference on World Wide Web. WWW ’17. International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, CHE, 765–774.
- Zhang, L., Xiong, X., Zhao, S., Botelho, A., and Heffernan, N. T. 2017. Incorporating rich features into deep knowledge tracing. In Proceedings of the Fourth (2017) ACM Conference on Learning @ Scale. L@S ’17. Association for Computing Machinery, New York, NY, USA, 169–172.
- Zhang, N., Du, Y., Deng, K., Li, L., Shen, J., and Sun, G. 2020. Attention-based knowledge tracing with heterogeneous information network embedding. In Knowledge Science, Engineering and Management, G. Li, H. T. Shen, Y. Yuan, X. Wang, H. Liu, and X. Zhao, Eds. Springer International Publishing, Cham, 95–103.
1https://osf.io/8vcfd/
2https://www.kaggle.com/competitions/edm-cup-2023
3https://new.assistments.org/
4A standard error of 0.125 implies that the 95% confidence interval for item success rate is approximately 0.5 wide
5https://www.kaggle.com/competitions/edm-cup-2023/leaderboard
6https://github.com/arghosh/AKT
7https://www.nctm.org/ccssm/