Abstract
Many colleges use AI-powered early warning systems (EWS) to provide support to students as soon as they start their first semester. However, concerns arise regarding the fairness of an EWS algorithm when deployed so early in a student’s college journey, especially at institutions with limited data collection capacity. To empirically address this fairness concern within this context, we developed a GPA prediction algorithm for the first semester at an urban Japanese private university, relying exclusively on demographic and pre-college academic data commonly collected by many colleges at matriculation. Then we assessed the fairness of this prediction model between at-risk and lower-risk student groups. We also examined whether the use of 33 novel non-academic skill data points, collected within the first three weeks of matriculation, improves the model. Our analysis found that the model is less predictive for the at-risk group than their majority counterpart, and the addition of non-academic skill data slightly improved the model’s predictive performance but did not make the model fairer. Our research underscores that an early adoption of EWS relying on pre-matriculation data alone may disadvantage at-risk students by potentially overlooking those who genuinely require assistance.Keywords
1. Introduction
With the rapid development of artificial intelligence (AI) in recent years, many colleges across the world have implemented Early Warning Systems (EWS) (Plak et al., 2022, Von Hippel and Hofflinger, 2021, Sclater et al., 2016, Hanover Research, 2014). EWS leverages AI to predict the risk that students will not succeed in college, and institutions intervene with students based on the predicted risk as early as possible (Plak et al., 2022). However, it is also known that AI sometimes overestimates the risk of individuals belonging to specific groups and makes unfair and discriminatory decisions against them (Angwin et al., 2016, Mehrabi et al., 2021). The concern over discrimination perpetrated by AI has grown stronger over the years. This concern is also relevant to EWS, where machine learning algorithms play a critical role in intervention decisions.
One characteristic of EWS is that it is an early intervention. Although the definition of “early” varies by institution, it is common for many universities to deploy EWS during the first semester (Hanover Research, 2014). In one survey, thirty-three percent of U.S. universities reported that they carry out EWS-based interventions within the first six weeks (Simons, 2011). The well-known Georgia State University EWS also intervenes within the first six weeks of enrollment (Georgia State University, nd). These pieces of circumstantial evidence suggest that many universities are trying to use an EWS to intervene with students as early as possible during their first semester.
Prior research has questioned the accuracy of predictive models that heavily rely on data available around matriculation when the model primarily consists of pre-college academic and demographic characteristics data (Von Hippel and Hofflinger, 2021). However, accuracy is not the only issue at play. When predictive accuracy consistently falls short for specific historically marginalized groups, the EWS can result in unfair decisions. For instance, the institution might fail to support students who need it, leading to lower grades or retention for these marginalized students (Yu et al., 2021). Conversely, the institution might provide unnecessary support to students who do not require it, diverting resources from students who are genuinely in need (Yu et al., 2021). In both cases, the flawed predictive model could harm marginalized students, perpetuating inequities in higher education. Therefore, it is essential to evaluate EWS not only for accuracy but also for fairness.
In recent years, the literature on predictive analytics has witnessed a gradual rise in articles that empirically investigate the fairness of student outcome prediction algorithms (Yu et al., 2020, Yu et al., 2021, Jiang and Pardos, 2021, Kung and Yu, 2020, Hutt et al., 2019, Kleinberg et al., 2018, Gardner et al., 2022, Gardner et al., 2023). However, none of these studies have yet addressed fairness concerns associated with the early adoption of EWS. It is crucial for both the literature and practitioners to consider whether this widespread practice has the potential to result in biases, inequalities, or discriminatory practices. This study aims to take this discussion further by examining the fairness of a predictive algorithm used in the early part of the first semester when the available predictors are limited to demographic and pre-college academic characteristics data. By focusing on this critical aspect, we hope to provide insights into how to develop more equitable EWS in higher education.
Another pivotal aspect this paper explores is the data capacity of universities. Many universities referenced in prior studies boast extensive student data. However, how representative they are of the global higher education landscape is debatable. For instance, well-equipped institutions can amass real-time data throughout the semester, capturing metrics like class attendance, advisor interactions, assignments, and mid-term results. Such data can be invaluable for identifying students lagging. Yet, many lower-resourced institutions face challenges in accumulating those data due to technical issues, staffing shortages, budget constraints, and other factors. As a result, they often depend on data available at matriculation, typically collected from administrative databases like applications. The capability of these data-limited institutions to effectively deploy EWS is a pressing concern for their stakeholders. Nevertheless, literature attention toward these types of universities remains limited. Exploring such data-constrained institutions could provide insights more representative than those garnered from the frequently studied, well-funded, data-rich institutions.
To fill this gap in the literature, we built an algorithm that predicts a student’s first-term college GPA, one of the earliest academic performance indicators that many universities pay close attention to (Gershenfeld et al., 2016). As prediction algorithms, we use logistic regression, Random Forest, and eXtreme Gradient Boosting, commonly referred to as XGB (Chen and Guestrin, 2016). For this study, we only use data available at matriculation, which essentially limits data availability to basic demographics and academic characteristics readily accessible at most universities with limited data collection capacity (hereafter, we refer to those data as “pre-matriculation data” in short). Then, we built a model to predict the likelihood of students with a first-term GPA below 2.0, calling this a “pre-matriculation data model”, and compared the model’s fairness between at-risk and lower-risk groups. We also later add a novel dataset comprising non-academic skill assessment scores over 33 dimensions, measured three weeks after the first semester begins. We examine whether prediction accuracy and fairness make a difference with or without the non-academic skill data. We refer to the latter model as an “augmented model.” We examined algorithmic fairness regarding Area Under the Curve (AUC) and calibration, which examines the extent to which the fraction of individuals whose risk manifests conditional on the predicted risk level is comparable between the two groups (Corbett-Davies and Goel, 2018).
Our analysis shows that the pre-matriculation data model shows a higher AUC for the lower-risk groups than the at-risk groups, suggesting that it has a fairness problem against the at-risk group. We also found that adding non-academic skill data slightly improves AUC for both groups, but the gap persisted. Our calibration analysis shows that the pre-matriculation data model disproportionately underestimates the risk at the lower end of the predicted risk spectrum within the at-risk group only. This calibration result implies that the model might overlook some students in the at-risk group who do not show obvious risk in the data (other than their group membership) but genuinely require assistance. Incorporating non-academic skill data does not significantly mitigate this issue. In summary, our study indicates that when using only data available at matriculation, first-term grade prediction models might result in inadequate support to marginalized students compared to their majority counterparts.
This study highlights a dilemma faced by professionals at institutions with limited data environments: striking a balance between timely interventions and equitable implementations of these actions. A simple solution is to collect more data that may predict outcomes, such as real-time data indicating student progress in college. However, they may not have the luxury of collecting such data in a systematic way for early warning purposes. One possible approach to consider for future exploration is a shared modeling strategy. In this approach, institutions can forecast student outcomes using predictive models trained on data from multiple other institutions (Gardner et al., 2023). These practices use transfer learning techniques, which are experimented with in some universities in the U.S. (Gardner et al., 2023). These techniques also might be useful in other nations, particularly where using student data for predictive analytic purposes is difficult due to privacy concerns and/or resource constraints. Understanding how to utilize transfer learning techniques for an EWS is an important future research area, especially in the context of algorithmic fairness for data-constrained institutions.
2. Literature Review
2.1. Early Warning Systems
An EWS is a part of Learning Analytics (LA) technology. Sometimes interchangeably used with predictive analytics (Ekowo and Palmer, 2016), LA aims to improve student’s educational outcomes and experiences by taking advantage of the data collected by the university (Sclater et al., 2016). An application of LA largely falls into the following three categories: 1) targeted student advising, 2) adaptive learning, and 3) enrollment management, and EWS belongs to the first category as it enables target advising by identifying at-risk students earlier in college (Ekowo and Palmer, 2016).
Hanover Research (2014) reported that about 90% of universities in the United States implement EWS. The use of EWS has also been reported across the world such as in U.K. and Australia (Sclater et al., 2016), Netherlands (Plak et al., 2022), and Chile (Von Hippel and Hofflinger, 2021). EWS uses machine learning and other statistical methods to detect students at risk of dropout (Plak et al., 2022). EWS’s application widely varies by institutions (Ekowo and Palmer, 2016), and dropout is one of many outcome variables that EWS predicts. Institutions also use EWS to predict other intermediate outcomes that could lead to dropout, such as poor grades (Macfadyen and Dawson, 2010, Dimeo, 2017).
EWS is attractive to many institutions partly because it is a low-cost intervention (Plak et al., 2022). Proactive student coaching is a promising practice to reduce college dropout (Bettinger and Baker, 2014), but it is also an expensive intervention. In reality, many institutions do not have adequate coaching or advising staff. One study reported that the average number of students served by a single full-time advisor is 269 at a four-year public university and 292 at a community college in the U.S. (Tyton Partners, 2022), suggesting that providing proactive student counseling to everyone is financially infeasible. EWS offers one solution to this cost-benefit dilemma: leveraging the power of data to identify students who need help and provide target interventions focused on those students. Doing so has the potential to compensate for inadequate student support due to the advisor shortage problem and solve the college dropout problem in a cost-efficient manner.
2.2. Algorithmic Fairness in Predictive Analytics
Scholars have discussed the fairness of student risk prediction models used for EWS under the theme of “algorithmic fairness” (Kung and Yu, 2020, Jiang and Pardos, 2021, Yu et al., 2021, Yu et al., 2020, Gardner et al., 2023, Kizilcec and Lee, 2022). Regarding algorithmic fairness criteria, a common consensus is that the algorithm does not discriminate against students based on their membership in a particular “protected group” (Kizilcec and Lee, 2022). It is originally a legal term, typically including demographic attributes such as gender, race, and age (Kizilcec and Lee, 2022). In the predictive analytics literature, the definition of “protected group” has been broadened to include characteristics that the individual cannot change (Kizilcec and Lee, 2022), such as geographic location (Paquette et al., 2020), learning speed or slowness (Doroudi and Brunskill, 2019), or first-generation college students (Yu et al., 2021).
Researchers typically measure algorithmic fairness from perspectives of “anti-classification,” “classification parity,” and “calibration” (Corbett-Davies and Goel, 2018). “Anti-classification” means that predictive modeling does not use protected attributes as predictors. “Classification parity” implies no difference in prediction accuracy across protected groups. “Calibration” means that the predictive accuracy of students with equivalent prediction risk is equal across protected groups (Corbett-Davies and Goel, 2018). Among those three fairness approaches, classification parity is a typical evaluation approach used in the prior empirical studies in the predictive analytics literature (Kung and Yu, 2020, Jiang and Pardos, 2021, Yu et al., 2021, Yu et al., 2020). However, classification parity metrics are known to bias in favor of the majority group in an imbalanced sample, making the validation result less reliable (Gardner et al., 2023). Thus this study follows Gardner et al. (2023), which suggested comparing AUC. In addition, we incorporate calibration into our evaluation for a more comprehensive assessment to better understand the model’s risk calculation mechanism.
The literature also discussed how to mitigate algorithm bias. Conceptually, a data analysis pipeline is comprised of data construction, model training, and inference/prediction stages (Mehrabi et al., 2021). Jiang and Pardos (2021) argues that algorithmic fairness can be compromised differently at each stage. They tested seven strategies intended to mitigate algorithm bias at different stages and argued that the one adopted at the model training stage mitigated algorithm bias the most. Kung and Yu (2020) also explored a way to reduce algorithm bias at the model training stage by testing whether several machine-learning algorithms have different prediction accuracy for course grades. They found that highly advanced machine learning algorithms are not necessarily fairer than simpler traditional models such as logistic regression. The result suggests that algorithmic fairness is not a function of model complexity.
Several studies discuss ways to mitigate bias at the data construction stage. Yu et al. (2020) examined whether adding Learning Management Systems (LMS) and survey data to an institution’s administrative data can improve algorithmic fairness in predicting grades for introductory STEM courses. They found that neither LMS nor survey data improved algorithmic fairness. Yu et al. (2021) examined whether a student retention prediction model should include protected group variables such as gender and first generation as predictors from an algorithmic fairness perspective. They found that the model becomes slightly fairer by having those group membership variables. Kleinberg et al. (2018) made a similar argument, finding that their college GPA prediction model using pre-college data became less accurate for minority groups by excluding the race variable.
Conceptually, our study is along the same lines as these previous studies concerning data construction in that we also address biases that may occur during the data construction phase. The previous literature discusses what data element to include or not include, such as demographic variables or log data from LMS. But the existing literature has not adequately addressed the significance of the timing of dataset construction in relation to the algorithm’s fairness. In fact, there is a notable lack of consistency regarding when models were developed across past studies. For example, Yu et al. (2020) utilize data available during an early phase of a given semester (not limited to the first college semester) to predict grades at the end of the same semester. Yu et al. (2021) employ data available at the end of the first semester to predict first-year retention, while Kleinberg et al. (2018)’s model relies on admission data to predict college GPA. We contend that determining an optimal time to build an EWS is a crucial question for practitioners. However, the literature has largely overlooked this aspect, resulting in ambiguity regarding when an algorithm for EWS should be developed from a fairness perspective.
Our study is also connected with a recent study by Gardner et al. (2023). They built a student dropout model for four different institutions and compared the predictive performance of the models using transfer learning techniques, which are in essence training models using data from other institutions. Specifically, they compared predictive performance of the following methods: 1) local model, 2) direct transfer, 3) voting transfer, and 4) stacked transfers. The local model, serving as a baseline, was developed using data specific to each institution, while the other methods utilized data from other institutions. Their findings showed that while the local model marginally outperformed the transfer learning methods, the disparity was not substantial. Notably, algorithmic fairness across subgroups remained consistent with the transfer learning methods. Our study is related to theirs in that they discuss the transition learning approach as a viable solution for data-constrained institutions, the primary target audience of our study.
Lastly, another element that the existing fairness literature has not adequately addressed is the significance of non-academic skill data in relation to the algorithm’s fairness. Numerous studies have reported that non-academic skills help predict college outcomes (e.g., Pickering et al. 1992, Adebayo 2008, Akos and Kretchmar 2017, Bowman et al. 2019, Farruggia et al. 2018, Fosnacht et al. 2019, Heckman et al. 2006, Akos et al. 2022), but it is not empirically established whether they help improve algorithmic fairness. We aim to fill this gap by investigating the relationship between fairness and non-academic skills data.
2.3. Research Questions
We have previously discussed in the introduction section that universities have aspirations to deploy EWS as early as possible during the first semester and create a statistical model by making the best of the data available. However, data typically available for statistical modeling during an early phase of the first semester for many lower-resourced institutions mainly consist of demographics and pre-college academic preparedness data such as high school GPAs, standardized test scores, and high school rankings. The question arises as to whether institutions can build a fair and equitable prediction model using such data alone, unlike some data-rich institutions which can obtain more granular data on student progress during the first semester such as class attendance, course assignments, mid-term grade etc. The goal of this study is to answer this question by addressing the following three research questions:
- To what extent is a student risk prediction algorithm using data available during the early phase of the first semester in college fair between student subgroups?
- To what extent does the algorithmic fairness of a student risk prediction algorithm improve after adding non-academic skill data?
- Why do non-academic skill data help improve algorithmic fairness (or not)?
The first research question provides a direct answer to the key question of this study stated above. The second question will discuss a potential solution if the model yielded unfair prediction results. In other words, if the algorithm of the model built during the first semester was not fair, will the model improve its fairness by using non-academic skill data? The third one is a mechanism question. By exploring a mechanism that drives algorithmic fairness, we seek to show how our findings can be replicated using other data from different settings and thereby ensure the external validity of the implications that emerged from this study. Lastly, as discussed previously, we examine “algorithmic fairness” via AUC and calibration comparisons.
3. Methods
3.1. Data
The data used in this study consist of student-level data of first-year students at an urban private university in Japan with an enrollment size of approximately 5,000. The sample size is 2,457 first-year students who first enrolled either in April 2016 or April 20171. The data included are: gender, age of initial matriculation, department, home prefecture, type of entrance examination, scores of English, Japanese, and mathematics achievement tests administered immediately after enrollment, high school ranking, high school grade, “PROG (Progress Report on Generic Skills)” scores which aim to measure both cognitive and non-cognitive abilities, GPA at the end of the first semester, and GPA at the end of the second semester. Race, family income, and first-generation status are not available. Japanese institutions rarely collect those data, in contrast to institutions in the Western hemisphere, such as U.S., where many universities collect those information. Table 1 shows a list of the variables available for this study, along with their means, minimum and maximum values, and additional notes if necessary.
One unique set of variables in our data is PROG scores. PROG is a generic skills assessment test run by the Kawaijuku Educational Institution, a private firm offering prep-school programs for entrance exams across various education levels. PROG aims to evaluate the general abilities, attitudes, and orientations that labor markets expect from university graduates, irrespective of their major or field of study. The PROG assessment is divided into two tests: the Literacy Test and the Competency Test. The Literacy Test gauges the ability to apply knowledge in problem-solving, while the Competency Test evaluates behavioral traits gained through experience. Unlike cognitive knowledge tests or self-diagnosis surveys, the PROG test seeks to assess how students apply knowledge and behave in practical contexts that they may face in their jobs after college. For example, PROG asks students questions assessing soft skills such as collaboration, teamwork, and leadership to solve real-life problems. The PROG measures both the cognitive and non-cognitive skills of students in 33 dimensions. All first-year students at this institution must take a PROG test at the end of April during the first semester at this university. This type of data may not be readily available at typical universities in other countries.
Also, this university administers mandatory aptitude tests to gauge students’ basic cognitive skills in English, Japanese, and mathematics during the first month of the first semester. These test scores allow us to understand their basic cognitive skill levels and supplement the information about pre-college academic skills in addition to high school GPA and ranking. Unlike remedial placement tests administered at many community colleges in the U.S., this is a low-stake test, meaning that the institution administers the test purely for self-assessment purposes and does not assign students to any intervention programs according to the result.
We assume that our dataset is largely comparable, at least conceptually, to what most institutions can typically obtain during the first semester from their administrative databases, except for PROG. The dataset consists of pre-college academic performance, basic academic skills, demographic characteristics, and other attributes, and they are known to be correlated with college student success (Adelman, 2006, Tinto, 2012, Pascarella and Terenzini, 2005, Kuh et al., 2011). Some institutions may have access to richer data that could help better predict, such as log data from LMS, more detailed demographic characteristics, and scores from mid-term tests, but they are not available for this study. Therefore, our results are more applicable to universities with relatively limited data capacity than universities that can exploit vast amounts of data.
| Predictors | Mean | MIN | MAX | Note |
|---|---|---|---|---|
| Male | 0.49 | 0 | 1 | Male = 1; Female = 0 |
| Department | NA | This college consists of 6 departments |
||
| Admission: Athlete and Cultural | 0.04 | 0 | 1 | Used with the other 6 admission category dummies |
| From the Same Prefecture as the Institution | 0.42 | 0 | 1 | Home address in the same prefecture = 1; otherwise = 0 |
| Recent HS Grad | 0.92 | 0 | 1 | Enrolled immediately after high school graduation = 1; otherwise = 0 |
| Matriculated in 2016 | 0.50 | 0 | 1 | Matriculated in 2016 = 1; 2017 = 0 |
| High School Rank | 13.01 | 1 | 20 | 1 is the Highest |
| High School GPA | 3.58 | 2.2 | 5 | Scale: 0 to 5 |
| Missing High School GPA | 0.02 | 0 | 1 | 1 if the student earned a GED-equivalent diploma |
| Assessment Test: Japanese | 67.2 | 6 | 100 | Assessed during the first 3 weeks since matriculation. Mandatory for all first-year students. |
| Assessment Test: Math | 38.7 | 0 | 85 | |
| Assessment Test: English | 50.1 | 8 | 95 | |
| PROG (Overall) | 2.39 | 1.19 | 4.13 | Average over 33 categories with each category ranging from the score of 1 to 5 |
| First-term GPA | 2.42 | 0 | 3.71 | Scale: A+=4, A=3, B=2, C = 1, D = 0. |
3.2. First-Term GPA Prediction Model
The dependent variable in the primary model is a first-term GPA. We chose this variable as the outcome of interest because the institution wants to improve college retention and on-time graduation in the long run. It seeks a near-term outcome that contributes to those outcomes and allows them to evaluate the progress in a short-term cycle. College grades are standard outcome metrics used in the predictive analytics literature (Mahzoon et al., 2018, O’Connell et al., 2018, Hart et al., 2017, Chen and Cui, 2020). In our dataset, the first-term GPA shows a high correlation (roughly 0.4) with on-time graduation. That relationship is consistent with the student success literature (Adelman, 2006, Pascarella and Terenzini, 2005), suggesting that how Japanese students progress in college is not markedly different from the patterns found in the previous literature, which primarily come from U.S. institutions. We convert GPA into a binary variable by considering a GPA below 2.0 as a low-performing student, assigning 1 to them and 0 to the rest. They roughly represent the bottom 20% of students. We adopt this threshold rule following the suggestion from the university officials, who perceive students with a 2.0 GPA as those with whom universities should be cautious. Finally, to better understand the algorithmic fairness of the prediction model in context, we built two different models using a different set of predictors. The first model uses the variables available during the early phase of the first semester shown in Table 1, except for PROG data (Model 1). The second model adds to Model 1 PROG scores, collected after a few weeks of the first semester (Model 2). Conceptually, we regard the first model as a “pre-matriculation data model” and the second as an “augmented model.”
Table 2 presents the fraction of students whose first-term GPA is below 2.0 for our sample (hereafter, we refer to GPA below 2.0 as “low-grade” and students with that grade as “low-grade students” for brevity). The first column displays the “risk factor”, encompassing the following categories: Gender, Department, Admission Type, and High School Ranking. These categories were chosen based on historical group-level grade data and university officials’ inputs regarding which student groups might require additional support, unlike typical Western risk factors, such as race, SES, or first-generation status, which are not collected at Japanese institutions. Nevertheless, these factors are also not changeable at matriculation, serving as a soft form of demographics in Japanese contexts. Furthermore, much like their Western counterparts, students with some or all of these factors might require support. Consequently, the predictive model needs to ensure these groups are not disadvantaged.
The overall low-grade rate is 19.1%. The male students’ low-grade rate is 28.3%, almost three times as high as the females’ rate, which is 10.3%. The “student’s department” categories break students into two groups. One is students who enrolled in department A, whose low-grade rate is 38.0%, higher than the other departments of 17.4%. In Japan, students are typically admitted by a department (not institution), and it is rare to switch a department after matriculation. Because each department sets its admission standard, the academic readiness of college entrants could vary from department to department. Next, the “admission” category consists of students admitted as college athletes or culturally talented individuals and those admitted through other admission channels. The low-grade rate for the former is 56.4% compared to 17.4% for the latter. The last category breaks students into low-ranking high schools and others. Daigaku Tsushin, a Japanese media firm specializing in college admission, releases high school rankings every year, ranking high schools on a scale of 1 to 20, the latter being the lowest. We define low-ranking high schools as those ranking at 17 or below, representing approximately the bottom 10% of first-year students at this university. Students from the low-ranking high school have a low grade rate at 30.5%, compared to the rest of the students at 18.0%. In this study, we consider students with at least two of these risk factors “at-risk students”, whose overall low-grade rate is 41.6%. They represent approximately 13% of the sample (315/2,457). The remaining students, whom we refer to as “lower-risk students”, have a low-grade rate at 15.9%.
| Risk Factor | N | GPA\(<\)2.0 | |
|---|---|---|---|
| Gender | |||
| Female | 1,244 | 10.3% | |
| Male | 1,209 | 28.3% | |
| Department | |||
| Department A | 205 | 38.0% | |
| Other Department | 2,248 | 17.4% | |
| Admission Type | |||
| Athlete and Cultural | 110 | 56.4% | |
| Other Admission | 2,343 | 17.4% | |
| High School Ranking | |||
| Low-Ranking HS | 236 | 30.5% | |
| Other HS | 2,217 | 18.0% | |
| At Least with Two Risk Factors | |||
| Yes | 315 | 41.6% | |
| No | 2,138 | 15.9% | |
| Overall | 2,457 | 19.1% |
Table 3 shows a list of PROG scores with mean and standard deviation for at-risk and lower-risk groups of students. It consists of three categories: basic interpersonal skills, task execution skills, and self-control skills. Each category further breaks out into three subcategories. Affinity, collaborative skills, and leadership skills comprise the basic interpersonal skills. The task-execution skills consist of problem identification, planning, and execution skills, while the self-control skills include emotional control skills, self-confidence-building skills, and perseverance. Each subcategory further breaks down more detailed categories, which sum up to 33. The list indicates that some data points, such as “information gathering” and “risk analysis,” may overlap with cognitive skills. However, a significant portion of these variables predominantly falls under non-cognitive ability. For this study, we categorize these data points under the umbrella term “non-academic skills.”
One notable finding from this table is that the overall average is higher for at-risk students than for lower-risk students. The average PROG score for the former is 2.79 compared to 2.60 for the latter. The findings contrast the GPA results in Table 2. However, they are not entirely unexpected. For example, a varsity student admitted through a sports pathway might academically underperform compared to the broader student body, but they could possess qualities like stress tolerance and grit. These data suggest that PROG might capture aspects not reflected in the other data and may make a unique contribution to the prediction model.
| At-risk | Lower-Risk
| |||
| Variable | Mean | SD | Mean | SD |
|---|---|---|---|---|
| Basic Interpersonal Skills
| ||||
| Affinity
| ||||
| Appreciating Diversity | 3.49 | 1.50 | 3.40 | 1.47 |
| Approachability | 3.14 | 1.41 | 2.73 | 1.52 |
| Attentiveness | 2.88 | 1.31 | 2.70 | 1.34 |
| Empathy | 3.07 | 1.38 | 2.90 | 1.37 |
| Networking Building | 2.88 | 1.36 | 2.38 | 1.37 |
| Trust Building | 3.14 | 1.46 | 2.94 | 1.45 |
| Collaborative Skills
| ||||
| Ability of Information Sharing | 2.86 | 1.38 | 2.44 | 1.38 |
| Collaborative Behavior | 3.22 | 1.52 | 3.02 | 1.59 |
| Motivating Others | 2.89 | 1.51 | 2.29 | 1.48 |
| Partnership Skill | 2.92 | 1.48 | 2.80 | 1.53 |
| Leadership Skills
| ||||
| Constructive Discussion | 2.54 | 1.32 | 2.31 | 1.29 |
| Coordinating Opinions | 2.55 | 1.25 | 2.24 | 1.25 |
| Discussion Skill | 2.61 | 1.39 | 2.29 | 1.26 |
| Express Opinion | 2.71 | 1.31 | 2.41 | 1.41 |
| Task Execution Skills
| ||||
| Problem Identification Skills
| ||||
| Attitude to Inquire Cause | 2.96 | 1.29 | 2.93 | 1.25 |
| Information Gathering | 2.63 | 1.26 | 2.55 | 1.26 |
| Understanding Essence | 2.21 | 1.33 | 2.38 | 1.41 |
| Planning Skills
| ||||
| Ability to Assess Plans | 2.41 | 1.39 | 2.53 | 1.38 |
| Goal Setting | 2.93 | 1.37 | 2.36 | 1.37 |
| Risk Analysis Skill | 2.23 | 1.29 | 2.56 | 1.40 |
| Scenario Building Skill | 2.38 | 1.29 | 2.34 | 1.28 |
| Execution Skills
| ||||
| Ability to Validate and Enhance | 2.97 | 1.41 | 2.89 | 1.43 |
| Action Orientedness | 2.81 | 1.52 | 2.48 | 1.38 |
| Adjustment Skills | 2.24 | 1.28 | 2.42 | 1.37 |
| Execution Skill | 3.06 | 1.47 | 2.67 | 1.44 |
| Self Control Skills
| ||||
| Emotional Control Skills
| ||||
| Coping Stress | 2.61 | 1.28 | 2.55 | 1.31 |
| Self Awareness | 3.28 | 1.54 | 3.50 | 1.54 |
| Stress Management | 2.95 | 1.48 | 2.28 | 1.36 |
| Self-Confidence Building Skills
| ||||
| Optimism | 2.55 | 1.31 | 2.19 | 1.28 |
| Recognizing individuality | 2.92 | 1.37 | 2.42 | 1.36 |
| Self-Motivation Skill | 2.56 | 1.23 | 2.42 | 1.27 |
| Perseverance
| ||||
| Establishing Positive Behavior | 2.98 | 1.36 | 3.19 | 1.26 |
| Proactiveness | 2.72 | 1.38 | 2.15 | 1.22 |
| Total | 2.79 | 0.56 | 2.60 | 0.55 |
Notes: At-risk students includes those who belong to at least two of the following groups: Male, Department A,
admitted through athlete and cultural tracks, or from a high school with the ranking 17 or above. The authors
translated each skill from Japanese into English.
3.3. Algorithms
As an algorithm for predicting students whose first-term GPA will fall below 2.0, this study uses three algorithms written in R. The first is logistic regression, and we do not tune any hyperparameters. The second algorithm is Random Forest, for which we set the number of trees at 100 and the number of variables randomly sampled at each split at \(\sqrt {p}\), where \(p\) is the total number of predictors. And the third one is XGB, an ensemble, non-linear tree-based model. Widely used by many data scientists, the XGB algorithm has demonstrated predictive superiority over other algorithms on many occasions (Chen and Guestrin, 2016). For a detailed description of XGB and how its algorithm works, we defer to Chen and Guestrin (2016). For XGB’s hyperparameters, we tuned the model, used the values through a grid search, and chose the combination that provided the best test result. For the model with and without PROG data, we set the learning rate (eta) at 0.01 and 0.1, the minimum child weight both at 1, the proportion of observations supplied to a tree (subsample) at 0.7 and 0.5, the proportion of predictors supplied to a tree (colsample_bytree) at 0.7 and 0.6, the maximum depth of a tree at 6 and 4, and the minimum amount of reduction required in the loss function to make a split (gamma) both at 0, respectively. We also set the number of trees (nround) at 100 for both models. Lastly, we do not use neural network-based models like deep learning. The literature is skeptical about their predictive performances in a tabular-data environment (see Gardner et al. 2022 for a more detailed review of the predictive performance of neural network-based models in tabular data). Because our data set is also in a tabular form, we take the same stance as this literature, opting out of neural network-based models.
3.4. Evaluation Criteria
For the fairness evaluation criterion, we compare the Area under the Curve (AUC), which gauges the model’s overall predictive performance, between the at-risk and the lower-risk groups. In addition, we also assess our model’s fairness using calibration. In this calibration method, we divide the predicted likelihood of low grade into ten groups, ranging from low to high, and plot them on the horizontal axis. We then determine the low-grade rate for each group and plot it on the vertical axis. Ideally, these results should align with a 45-degree line, signifying a match between the predicted likelihood and actual rates of having low grades. For the model to be considered fair, this relationship between predicted risk and actual fraction of low-grade recipients should consistently line up on the 45-degree line, regardless of whether students are in the at-risk or the lower-risk group.
Model evaluation is performed by dividing the training and test data by 8 to 2 and using a five-fold cross-validation method. We repeat this process twenty times to obtain reliable standard errors of the AUC and calibration metrics. We calculate the average performance of the 100 test results (five-fold over twenty iterations) and standard errors.
4. Results
4.1. AUC Comparison
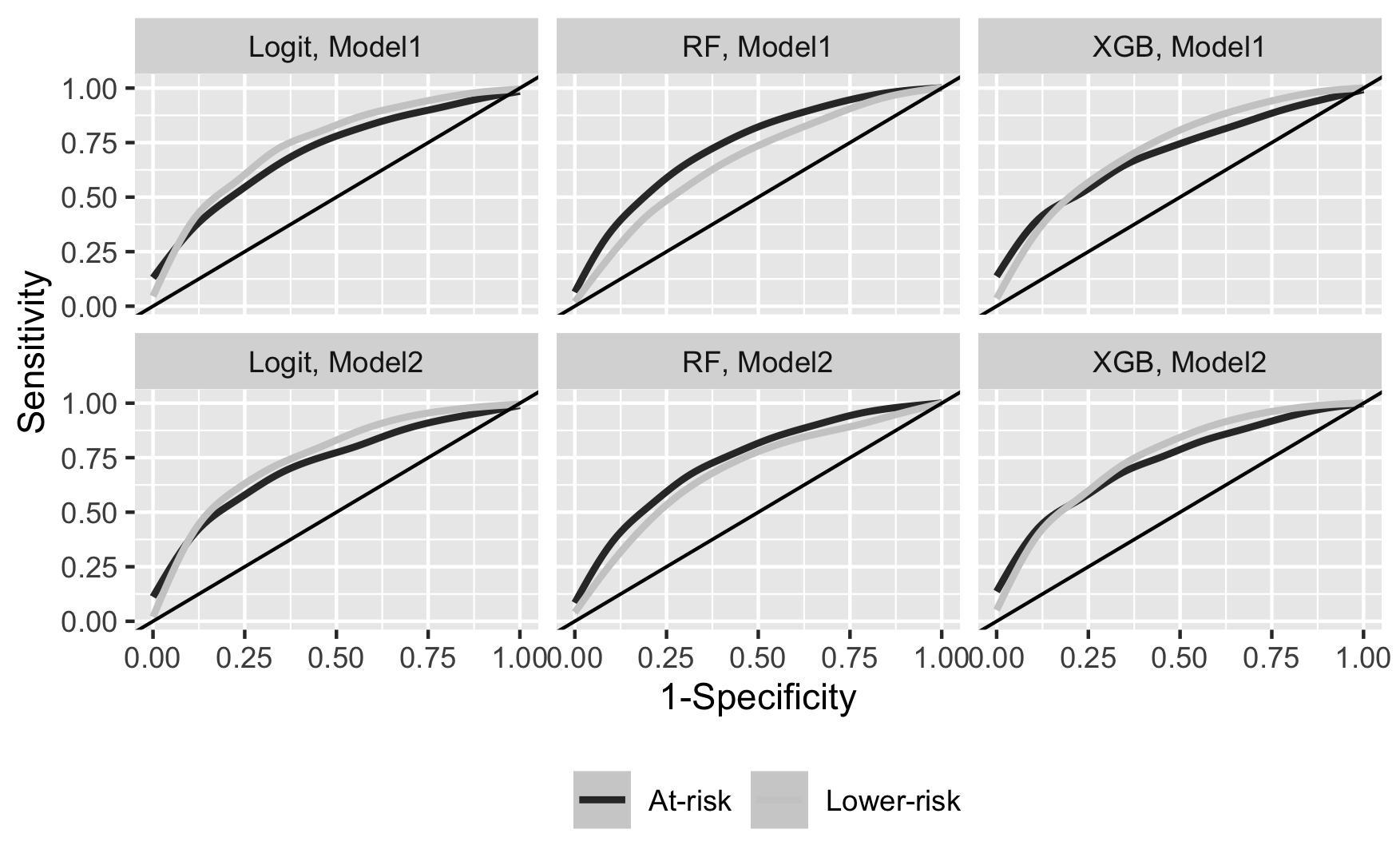
Table 4 showcases the model’s validation results for at-risk and lower-risk student groups, segmented by the algorithm: Logistic Regression, Random Forest, and XGB. For each algorithm, the table provides AUC for both “Model 1” (without non-academic skill data) and “Model 2” (with non-academic skill data). The former corresponds to the pre-matriculation data model, while the latter refers to the augmented model. The “Diff” rows highlight the differences between the two student groups within the same model. We also present Figure 1 as a visual aid to Table 4, showing Receiver Operating Characteristic (ROC) curves between at-risk and lower-risk groups across the models and algorithms.
Our AUC results highlight a performance discrepancy between the at-risk and lower-risk student groups. With Logistic Regression, Model 1 (the pre-matriculation data model) exhibits a -0.04 AUC gap, indicating superior predictive accuracy for the lower-risk students. In contrast, the Random Forest algorithm shows a 0.07 AUC advantage for at-risk students, a result that deviates from the Logistic Regression findings. However, considering the poor calibration of the Random Forest algorithm depicted in Figure 2 (which we will delve into in the subsequent subsection), we are inclined to regard the Logistic Regression outcomes as more trustworthy. The XGB model’s AUC gap stands at -0.02, suggesting again a better prediction for the lower-risk students. Meanwhile, the gap is smaller than the other two algorithms. The smaller gap is consistent with (Gardner et al., 2022), which shows that XGB had the lowest prediction gap among subgroups compared to other neural network-based algorithms. Notably, incorporating non-academic skills (i.e., Model 2, the augmented model) slightly improves AUC for both the groups with Logistic Regression and XGB, but the gap remained unchanged. In summary, the first-term GPA prediction model with the pre-matriculation data exhibits fairness issues concerning marginalized students. While incorporating non-academic skill data enhances accuracy to some extent, it does little to address the fairness concern.
| Model 1 (without PROG) | Model 2 (with PROG)
| |||
|---|---|---|---|---|
| Type | Mean | SE | Mean | SE |
| Logistic Regression
| ||||
| At Risk | 0.71 | 0.01 | 0.72 | 0.01 |
| Lower Risk | 0.75 | 0.00 | 0.76 | 0.00 |
| Diff | -0.04 | 0.01 | -0.03 | 0.01 |
| Random Forest
| ||||
| At Risk | 0.74 | 0.00 | 0.74 | 0.00 |
| Lower Risk | 0.67 | 0.01 | 0.69 | 0.01 |
| Diff | 0.07 | 0.01 | 0.05 | 0.01 |
| XGB
| ||||
| At Risk | 0.70 | 0.01 | 0.74 | 0.01 |
| Lower Risk | 0.73 | 0.00 | 0.76 | 0.00 |
| Diff | -0.02 | 0.01 | -0.02 | 0.01 |
Note: 1) The outcome variable is whether the student have a first-term GPA below 2.0. 2) “Model 1” corresponds
the pre-matriculation data model which only uses demographic and pre-college academic characteristics shown in
Table 1. 3) “Model 2”, or the augmented model, adds PROG data.
4.2. Calibration
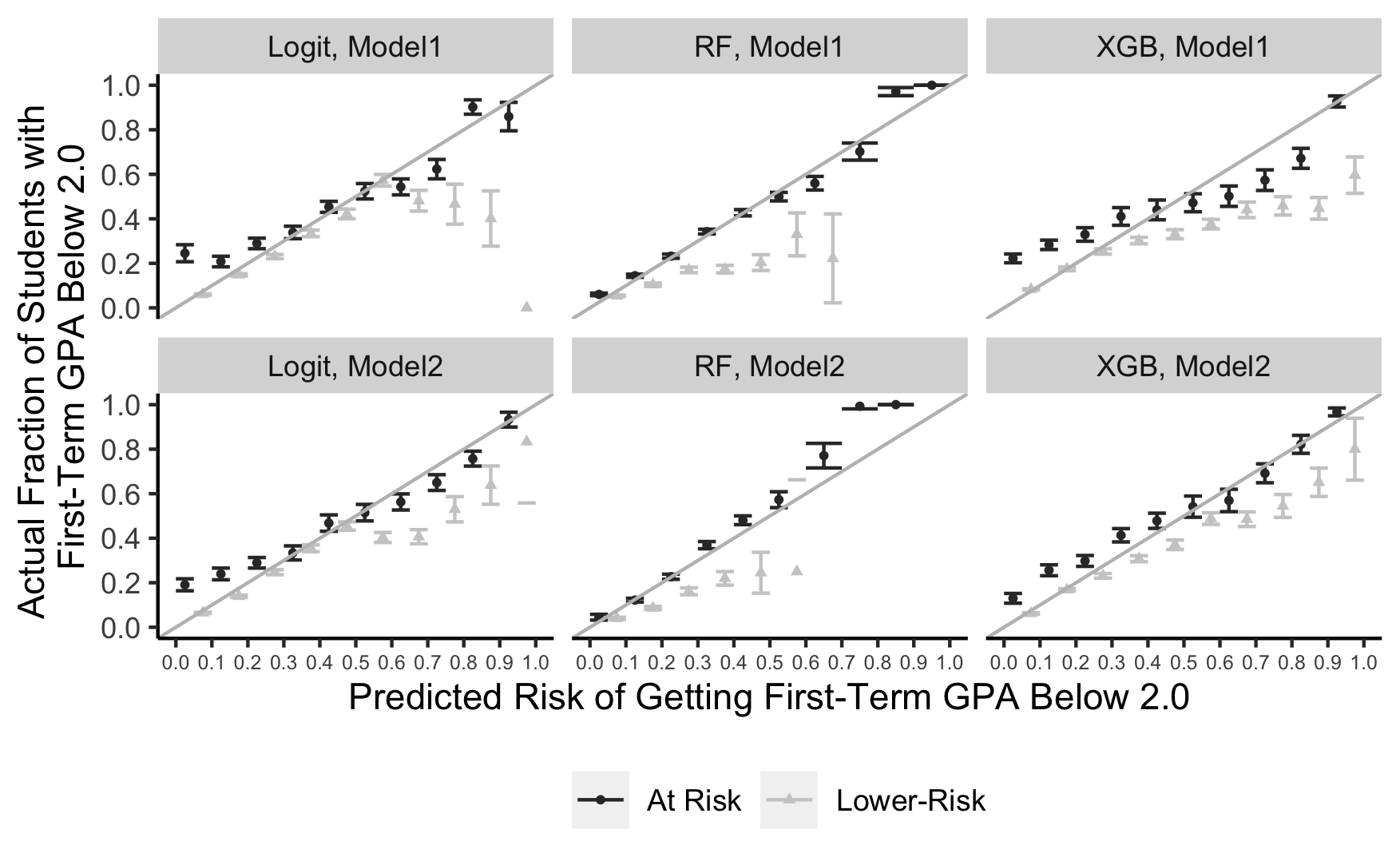
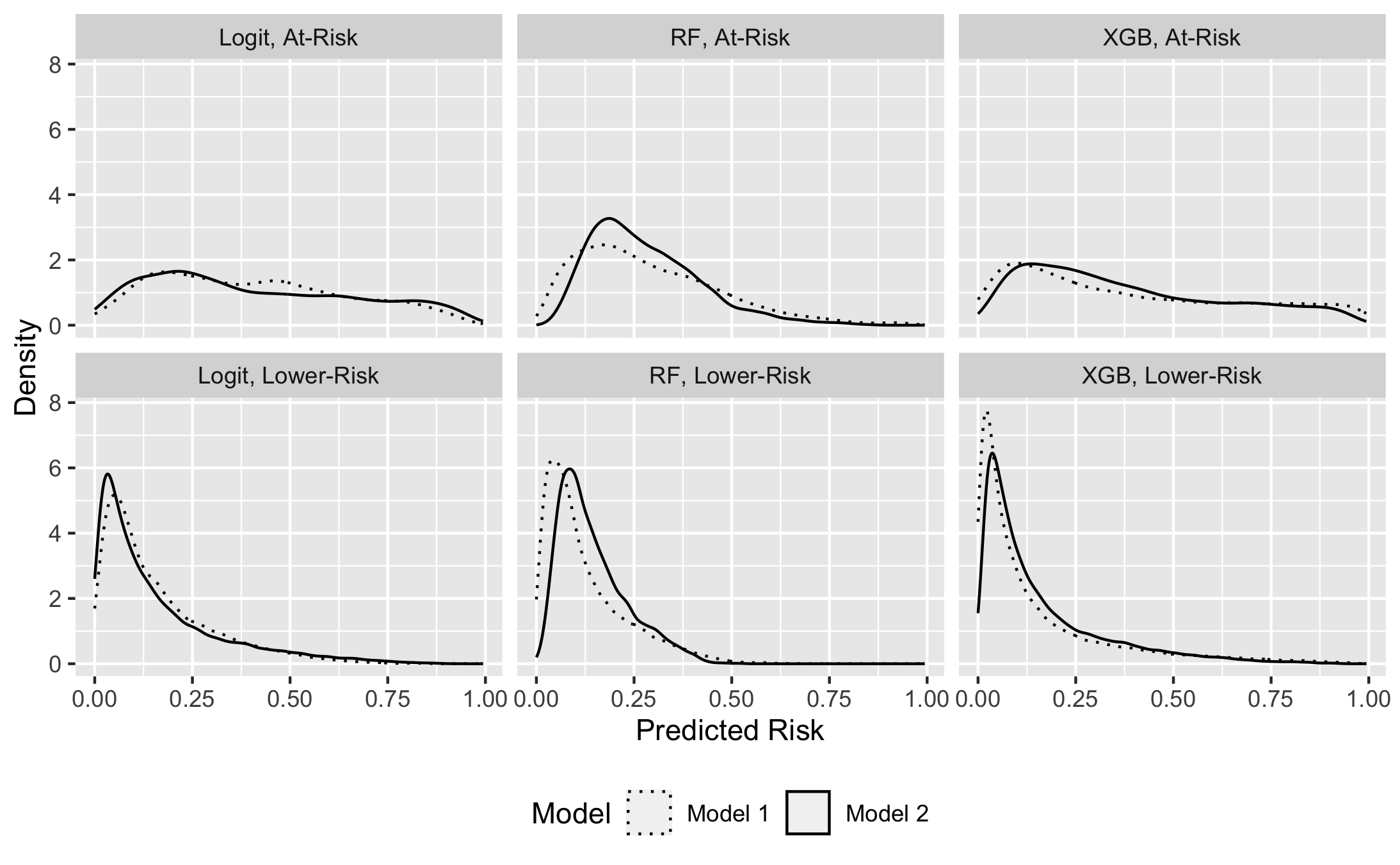
Figure 2 presents the calibration results for logistic regression, Random Forest, and XGB. The predicted risk is segmented into ten groups along the x-axis in each visual representation, while the actual fraction of underperforming students is plotted on the y-axis. The error bars, distinguished by triangle marks for lower-risk students and circles for at-risk ones, indicate variations in calibration results. The gray diagonal lines depict the ideal calibration scenario, corresponding to a 45-degree line representing perfect alignment between predicted and actual outcomes. In addition, as an aid to better interpret the calibration result, we present Figure 3, which maps the density distribution of predicted risks for both the at-risk (above) and lower-risk groups (below) across the three algorithms. Each panel shows two lines, with the solid line representing the model without PROG data and the dashed line corresponding to the model with PROG data.
In Model 1 (Pre-Matriculation Data Model), a visual assessment reveals that the logistic regression model demonstrates relatively better calibration results than the other two algorithms, as most data points closely align with the 45-degree line. We find a notable calibration dip for the lower-risk students toward the higher end of the risk spectrum. However, Figure 3 shows that only a tiny fraction of students fall into this high-risk probability range, suggesting that the calibration issue for the lower-risk group primarily affects a niche student segment. The logistic regression model faces the most significant calibration challenge for the at-risk students closer to the lower end of the risk spectrum. The model tends to underestimate their risks (Figure 2), and there is a notable number of at-risk students clustering in this area, as shown by the solid line in the top-left chart in Figure 3. The miscalibration observed for these students likely explains the lower AUC discussed earlier. In other words, the prediction model might overlook some at-risk students who require support but exhibit little observable risk characteristics.
The calibration of the Random Forest model aligns reasonably with the 45-degree line for at-risk students. However, this alignment veers off the 45-degree mark for the majority counterpart, and the deviation intensifies with increasing predicted probability. Additionally, the absence of data beyond the 70% predicted risk implies the model’s failure to recognize any student from the lower-risk group as being at high risk of underperformance, which is likely to be an unrealistic assessment. As discussed earlier, these calibration flaws likely explain the model’s reduced AUC for the lower-risk group, underscoring the algorithm’s limited credibility.
For the XGB model, the calibration pattern is reminiscent of that seen in the logistic regression model, as it also tends to underestimate the risk for the at-risk students positioned toward the lower end of the risk spectrum and overestimate the risk for lower-risk students located toward the higher end of the spectrum. Just like in the logistic regression model, only a few students in the lower-risk group have a higher risk of low grades (as evident in Figure 3), indicating that the subpar calibration for those students has minimal impact on the lower-risk group. However, compared to the logistic regression results, the degree of miscalibration is more pronounced for the XGB model. This finding aligns with the observation that the AUC is higher for the logistic regression model than the XGB model, as shown in Table 4.
In Model 2 (Augmented Model), adding non-academic skill data improved the XGB model’s performance, as seen in Figure 2. There was also a visible enhancement in the logistic regression. However, both models still exhibited the miscalibration trend for at-risk students at the lower end of the predicted risk spectrum, similar to what was observed in Model 1. On the other hand, the Random Forest model’s calibration continued to have the same problem seen in Model 1. These results suggest that while introducing non-academic skill data might improve model calibration overall, it does not sufficiently address the issue of overestimating risks for marginalized students, especially those who do not exhibit much risk in the data beyond their group membership. Despite their lower risk profile in the data, these students may still require assistance, and using non-academic skill data does not help identify them. This explains why including non-academic skill data led to a better AUC while leaving the AUC disparity unchanged.
Figure 3, which compares the distribution of predicted risks with and without the incorporation of non-academic skill data, shows noticeable shifts in the risk distribution when non-academic skill data are added. However, the direction of these shifts is not consistent across algorithms and subgroups, making it challenging to provide a straightforward interpretation. Essentially, the figure demonstrates that while non-academic skill data can have some impact on the distribution of predicted risks, their contribution to the model is limited.
5. Discussion
5.1. Algorithmic Fairness of First-term GPA Model Under Data-Constrained Scenarios
Our study discovered that a first-term GPA prediction model, which relies on early semester data, has fairness issues. Specifically, it shows reduced predictive accuracy for the at-risk group. The findings imply that models relying solely on matriculation data might face challenges in accuracy, as pointed out by Von Hippel and Hofflinger (2021), and fairness. This insight is particularly relevant for practitioners at institutions with limited data collection capabilities, where the most accessible data encompasses only demographics and a handful of pre-college academic characteristics.
Algorithmic fairness is not just a methodological issue. Our study found that the model tends to underestimate the risk of students in the at-risk group, especially among those at the lower end of the risk distribution. Because these students exhibit little observable problems in our data besides their group membership, the model believes they have a low chance of getting poor grades. However, in reality, their risk is higher than predicted. This means these students may fail to receive the support they need. In contrast, this issue of oversight is not present for students in the lower-risk group, suggesting that algorithmic unfairness may harm educational equity.
Globally, universities differ significantly in their data collection capabilities. Some institutions, frequently highlighted in the literature, boast expansive datasets. In contrast, many others work with limited data. It is worth noting that institutions with fewer resources often have more students requiring assistance. Our findings imply that implementing an EWS during the initial phase of the first semester in such a data-constrained environment could further compromise educational equity.
5.2. Role of Non-Academic Skills Data
Another intriguing discovery from our research is that while the inclusion of non-academic skill data enhances the model’s predictive accuracy (as indicated by AUC), the performance disparity persists. Past studies on non-academic skills have consistently demonstrated a favorable correlation with diverse student outcomes (see Pickering et al. 1992, Adebayo 2008, Akos and Kretchmar 2017, Bowman et al. 2019, Farruggia et al. 2018, Fosnacht et al. 2019, Heckman et al. 2006, Akos et al. 2022). The observed AUC improvement upon integrating non-academic skill data aligns well with the existing literature. Meanwhile, it is less recognized that they do not necessarily enhance the predictive performance gap. The minimal impact of non-academic skills on algorithmic fairness is an important contribution to the existing literature.
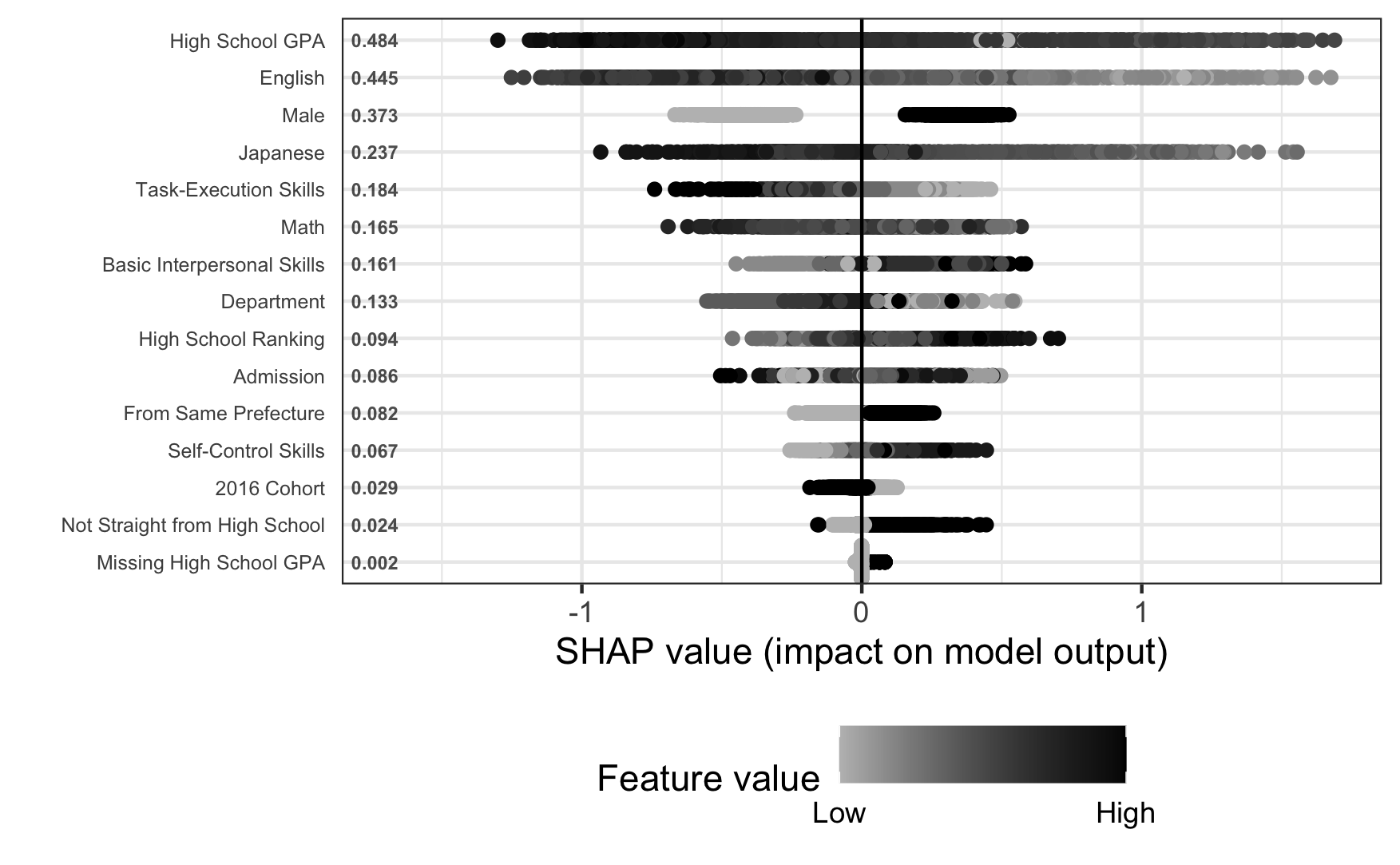
To better understand the roles of non-academic skill data in the model, Figure 4 displays the SHapley Additive exPlanations, known as SHAP, results of the XGB model. Our choice to highlight the XGB model was driven by its superior AUC and its satisfactory calibration performance. XGB’s superior performance is also consistent with Gardner et al. (2022), which provides additional validation to our model selection. In their article, they demonstrated that XGB has shown superior “subgroup robustness” than neural network-based methods in that 1) a subgroup variation in predictive performance is smaller and 2) the lowest subgroup performance is higher for the former than the latter (Gardner et al., 2022, page 1). While logistic regression also showcased a similar predictive capability, we leaned toward XGB. This decision was predominantly due to space constraints; presenting the coefficients of all predictors in logistic regression becomes cumbersome, especially given the multitude of dummy variables involved. Furthermore, for clarity in the presentation, we have opted to utilize three aggregated PROG skills rather than the original 33 variables. They are Basic Interpersonal Skills, Self-Control Skills, and Task Execution Skills. While the AUC is marginally lower with these three combined PROG skills than with the 33 individual variables, the difference is not significant enough to alter the paper’s primary argument. We believe that displaying the SHAP value of these three consolidated PROG variables will enhance the presentation of our results.
Proposed by Lundberg and Lee (2017), SHAP aims to explain what goes on inside the black box of machine learning. In essence, it applies a concept of cooperate game theory to estimate the extent to which each predictor contributes to the model (Trevisan, 2022). Unlike feature importance, which only shows the magnitude of the variable’s contribution in an absolute term, SHAP generates coefficient-like values spanning both positive and negative directions. Also, the predictor’s SHAP values vary by observations, allowing us to show heterogeneity in the role of predictors among students visually compellingly.
The figure consists of three dimensions, with each dot representing an observation in the data. The first dimension is the vertical axis, which shows the feature variables in descending order by the overall contribution to the model as determined by the average SHAP value across all observations. The next dimension is the horizontal axis, which indicates the direction of the feature’s contribution to the risk. If the feature increases the risk, the dots lean toward the right. If the feature lowers the risk, the dots are located toward the left. The third dimension is the color of the dots, with a lighter grey meaning that the value in the variable is lower and a darker black indicating that the value is higher.
The model ranks high school GPA as the most influential predictor. The predominance of lighter dots for the high school GPA stretching toward the right suggests that the model perceives students with lower high school GPAs as riskier. English test scores follow the next, demonstrating a spread of SHAP values slightly narrower than the high school GPA. These results indicate that English test scores nearly match the influence of high school GPAs in the model. Other significant variables include gender (specifically being male), Japanese test scores, and math scores.
Among the non-academic skills, task execution skills are the most influential in the model, ranking 5th in overall contribution to the model. The concentration of darker dots on the left implies that individuals with higher levels of these skills are deemed less likely to have low grades. This skill consists of problem identification, planning, and execution skills. Beattie et al. (2018) also found that low-college grader students tend to have a higher propensity for procrastination. Thus, the positive correlation between task execution skill and GPA in our model is aligned with the literature, providing an additional layer of confirmation to the role of non-academic skills in grade prediction. However, their SHAP value spread is less than half of what we see for high school GPA or English test scores and the overall contribution. This result suggests that while non-academic skills are relevant to first-term GPA, they are not as influential as predictors that primarily assess cognitive abilities.
However, it is important to remember that the SHAP values do not indicate causation, and they should be interpreted cautiously. For instance, the SHAP figure suggests that being male increases risk in the model. However, this is likely a manifestation of societal and structural factors leading to gender disparities, not a direct causation. Another case in point is the inverse correlation between interpersonal and self-control skills with GPA in our study, which contradicts established literature. However, this relationship in our data might be misleading as well. Consider varsity students: They may possess strong interpersonal and self-control skills, but if they are extensively engaged in games and practices at the expense of their studies, their academic performance could decline. Without accounting for the depth of their varsity engagement, our model might incorrectly infer a negative correlation between these skills and GPA. Their extensive involvement in varsity activities might influence their GPA, not their non-academic skills. A more comprehensive understanding of students’ extracurricular activities is essential to gauge the connection between PROG scores and GPA accurately. Such misleading correlations arise when the model overlooks a crucial predictor. In essence, these SHAP values reflect mere mechanical correlation based on the provided data, not necessarily the true relationships in the real world.
Lastly, collecting non-academic skill data often poses a challenge for many institutions. Integrating such data into regular collection cycles may demand significant organizational restructuring and coordination between various units and databases. The effort might justify the cost if non-academic skill data significantly enhanced predictions. However, our study indicates that the incremental benefit of adding non-academic skill data, in terms of accuracy and fairness, might be minimal at best. This is not to say that non-academic skill data are not valuable. Rather, while these data are associated with outcomes, their impact on predictive performance may not be substantial enough to warrant drastic changes in the institution’s data collection routine to detect students who need assistance.
6. Conclusion
Our study discovered that a first-term GPA prediction model that utilizes pre-matriculation data displays fairness issues toward the at-risk group. Specifically, it tends to overlook students in this group who may not show observable risks in the data but require assistance. Incorporating non-academic skill data can marginally enhance the model’s predictive performance. However, this addition does not effectively address the underlying fairness issue. These results suggest that 1) pre-matriculation data prediction models, which solely rely on data available at matriculation, might grapple with fairness challenges, and 2) the advantages of integrating non-academic skill data are limited when aiming to create equitable prediction models. The previous literature has not adequately discussed algorithmic fairness for EWS deployed in the early phase of the first semester when available data are only limited to demographic and pre-college academic characteristics. Our research contributes to this discussion, highlighting that deploying EWS during the initial stages of the first semester in such data-limited scenarios can result in biased outcomes against marginalized students.
Our research also informs the discussion on the timing for introducing an Early Warning System (EWS), a pivotal consideration for practitioners that has remained underexplored in academic literature despite its profound ramifications. Our findings suggest that implementing an EWS immediately after matriculation might not be the most judicious choice regarding fairness, particularly for institutions with constrained resources and data capacities. While this study does not determine the ideal timing for deployment, future research focusing on this aspect would be a valuable direction to explore.
Our study also highlights a dilemma encountered by lower-resourced institutions. They often have a higher proportion of students struggling in college, making implementing an early warning system particularly valuable. Yet, our research reveals that an early prediction model at such institutions may risk overlooking students who should receive support, especially among marginalized students. In an ideal scenario, those institutions can improve the model’s accuracy and fairness by collecting more variables that are not currently collected but have been shown to be related to college outcomes. For example, studies have indicated that aspects like a student’s adjustment to college life, their involvement, and engagement play pivotal roles in their academic success (e.g., Astin 1984, Kuh et al. 2008, Pascarella and Terenzini 2005, Tinto 2012). Also, a recent study by (Bird et al., 2022) demonstrated that including LMS data alongside administrative data significantly enhanced the predictive performance of their course grade prediction model for first-year students. However, expanding data collection capacity that way may not be feasible for those institutions.
One possible solution suggested in recent literature is cross-institutional transfer learning (Gardner et al., 2023). It builds a prediction model trained on data collected from different institutions. This approach appeals to universities with lower-resourced institutions that cannot collect a sufficient set of predictors. There is a concern that utilizing data from other universities might slightly diminish accuracy, but Gardner et al. (2023) contend that this reduction is not substantial enough to discredit the model. Yet, the implementation of transfer learning in higher education EWS is still in its early stages, with many aspects awaiting more clarity, including the choice of data types, protecting data privacy and security, and potential unexpected consequences. Future research on transfer learning holds significant value for lower-resourced institutions.
As another future research direction, the literature will probably gain valuable insights by comparing risk prediction models across different domains beyond education. For example, the Correctional Offender Management Profiling for Alternative Sanctions (COMPAS), which calculates a criminal defendant’s risk of committing another crime, has attracted criticisms for its biased behaviors against Black individuals (Angwin et al., 2016). However, its algorithmic fairness is satisfactory when using a calibration lens (Flores et al., 2016, Dressel and Farid, 2018). In comparison, our calibration analysis shows that the model is not algorithmically fair by “underestimating” the risk for at-risk students with little observable risk characteristics. The discrepancy in the calibration result between our and the COMPAS results indicates that there may be a unique mechanism that causes bias against marginalized individuals only in educational data but not in data sets from other domains. Exploring risk prediction models across different domains may help further understand the more intricate inner workings of risk prediction models in the higher education domain.
Lastly, we acknowledge the need for further research to validate our findings. It is important to note that our study’s generalizability needs further confirmation since we used data from a single private university in Japan. Results could differ when examining data from other universities in Japan or other countries, where college grading practices are substantially different and/or at-risk students may not share the same risk characteristics as our sample. Replicating our study using data from diverse countries is required to validate our study’s findings effectively.
Another limitation is that the PROG data might not accurately capture non-academic skills due to potential measurement errors. How non-academic skill data contribute to the model may vary when collected through different methods. Additionally, the impact of non-academic skill data on the model may depend on the specific outcome variable being used. Our study observed a slight improvement in AUC by incorporating PROG data into the model. However, different results might emerge if we used a different outcome variable, such as college dropout. First-term GPA may predominantly reflect cognitive skills. The limited enhancement brought by non-academic skill data could be partly attributed to the nature of this outcome. Non-academic skills may play a more substantial role in outcomes like college dropout or graduation, which are not solely dependent on cognitive abilities (Tinto, 2012). Further research to confirm the role of non-academic skill data in student risk prediction models across various outcomes is also an essential direction for future investigation.
7. Acknowledgments
This work was supported by the Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (KAKENHI) Grant Numbers 21K20231 and 23K12821. The views and opinions expressed in this manuscript are those of the authors and do not necessarily reflect those of JSPS.
References
- Adebayo, B. 2008. Cognitive and non-cognitive factors: Affecting the academic performance and retention of conditionally admitted freshmen. Journal of College Admission 200, 15–21.
- Adelman, C. 2006. The toolbox revisited: Paths to degree completion from high school through college. US Department of Education.
- Akos, P., Greene, J. A., Fotheringham, E., Raynor, S., Gonzales, J., and Godwin, J. 2022. The promise of noncognitive factors for underrepresented college students. Journal of College Student Retention: Research, Theory & Practice 24, 2, 575–602.
- Akos, P. and Kretchmar, J. 2017. Investigating grit at a non-cognitive predictor of college success. The Review of Higher Education 40, 2, 163–186.
- Angwin, J., Larson, J., Mattu, S., and Kirchner, L. 2016. Machine bias. https://www.propublica.org/article/machine-bias-risk-assessments-in-criminal-sentencing. Accessed: 11-22-2022.
- Astin, A. W. 1984. Student involvement: A developmental theory for higher education. Journal of College Student Personnel 25, 4, 297–308.
- Beattie, G., Laliberté, J.-W. P., and Oreopoulos, P. 2018. Thrivers and divers: Using non-academic measures to predict college success and failure. Economics of Education Review 62, 170–182.
- Bettinger, E. P. and Baker, R. B. 2014. The effects of student coaching: An evaluation of a randomized experiment in student advising. Educational Evaluation and Policy Analysis 36, 1, 3–19.
- Bird, K. A., Castleman, B., Song, Y., and Yu, R. 2022. Is big data better? LMS data and predictive analytic performance in postsecondary education (edworkingpaper: 22-647). Annenberg Institute at Brown University.
- Bowman, N. A., Miller, A., Woosley, S., Maxwell, N. P., and Kolze, M. J. 2019. Understanding the link between noncognitive attributes and college retention. Research in Higher Education 60, 135–152.
- Chen, F. and Cui, Y. 2020. Utilizing student time series behaviour in learning management systems for early prediction of course performance. Journal of Learning Analytics 7, 2, 1–17.
- Chen, T. and Guestrin, C. 2016. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD 2016. Association for Computing Machinery, New York, NY, USA, 785–794.
- Corbett-Davies, S. and Goel, S. 2018. The measure and mismeasure of fairness: A critical review of fair machine learning. arXiv preprint arXiv:1808.00023.
- Dimeo, J. 2017. Data dive. https://www.insidehighered.com/digital-learning/article/2017/07/19/georgia-state-improves-student-outcomes-data Accessed: 11-22-2022.
- Doroudi, S. and Brunskill, E. 2019. Fairer but not fair enough on the equitability of knowledge tracing. In Proceedings of the 9th International Conference on Learning Analytics & Knowledge. LAK 2019. Association for Computing Machinery, New York, NY, USA, 335–339.
- Dressel, J. and Farid, H. 2018. The accuracy, fairness, and limits of predicting recidivism. Science advances 4, 1, eaao5580.
- Ekowo, M. and Palmer, I. 2016. The promise and peril of predictive analytics in higher education: A landscape analysis. Policy paper, New America.
- Farruggia, S. P., Han, C.-W., Watson, L., Moss, T. P., and Bottoms, B. L. 2018. Noncognitive factors and college student success. Journal of College Student Retention: Research, Theory & Practice 20, 3, 308–327.
- Flores, A. W., Bechtel, K., and Lowenkamp, C. T. 2016. False positives, false negatives, and false analyses: A rejoinder to machine bias: There’s software used across the country to predict future criminals. and it’s biased against blacks. Fed. Probation 80, 38.
- Fosnacht, K., Copridge, K., and Sarraf, S. A. 2019. How valid is grit in the postsecondary context? a construct and concurrent validity analysis. Research in Higher Education 60, 803–822.
- Gardner, J., Popovic, Z., and Schmidt, L. 2022. Subgroup robustness grows on trees: An empirical baseline investigation. Advances in Neural Information Processing Systems 35, 9939–9954.
- Gardner, J., Yu, R., Nguyen, Q., Brooks, C., and Kizilcec, R. 2023. Cross-institutional transfer learning for educational models: Implications for model performance, fairness, and equity. In Proceedings of the 2023 ACM Conference on Fairness, Accountability, and Transparency. FAccT 2023. Association for Computing Machinery, New York, NY, USA, 1664–1684.
- Georgia State University. n.d. Student success programs at Georgia State. https://success.students.gsu.edu/early-alert/ Accessed: 11-22-2022.
- Gershenfeld, S., Ward Hood, D., and Zhan, M. 2016. The role of first-semester gpa in predicting graduation rates of underrepresented students. Journal of College Student Retention: Research, Theory & Practice 17, 4, 469–488.
- Hanover Research. 2014. Early alert systems in higher education. Tech. rep. https://www.hanoverresearch.com/wp-content/uploads/2017/08/Early-Alert-Systems-in-Higher-Education.pdf Accessed: 11-22-2022.
- Hart, S., Daucourt, M., and Ganley, C. 2017. Individual differences related to college students’ course performance in calculus II. Journal of Learning Analytics 4, 2, 129–153.
- Heckman, J. J., Stixrud, J., and Urzua, S. 2006. The effects of cognitive and noncognitive abilities on labor market outcomes and social behavior. Journal of Labor Economics 24, 3, 411–482.
- Hutt, S., Gardner, M., Duckworth, A. L., and D’Mello, S. K. 2019. Evaluating fairness and generalizability in models predicting on-time graduation from college applications. In Proceedings of the 12th International Conference on Educational Data Mining, C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. EDM 2019. International Educational Data Mining Society, 79–88.
- Jiang, W. and Pardos, Z. A. 2021. Towards equity and algorithmic fairness in student grade prediction. In Proceedings of the 2021 AAAI/ACM Conference on AI, Ethics, and Society. AIES 2021. Association for Computing Machinery, New York, NY, USA, 608–617.
- Kizilcec, R. F. and Lee, H. 2022. Algorithmic fairness in education. In The Ethics of Artificial Intelligence in Education, W. Holmes and K. Porayska-Pomsta, Eds. Routledge, New York, NY, 174–202.
- Kleinberg, J., Ludwig, J., Mullainathan, S., and Rambachan, A. 2018. Algorithmic fairness. In American Economic Association Papers and Proceedings, W. R. Johnson and K. Markel, Eds. Vol. 108. American Economic Association, 22–27.
- Kuh, G. D., Cruce, T. M., Shoup, R., Kinzie, J., and Gonyea, R. M. 2008. Unmasking the effects of student engagement on first-year college grades and persistence. The Journal of Higher Education 79, 5, 540–563.
- Kuh, G. D., Kinzie, J., Buckley, J. A., Bridges, B. K., and Hayek, J. C. 2011. Piecing together the student success puzzle: Research, propositions, and recommendations: ASHE higher education report. Vol. 116. John Wiley & Sons.
- Kung, C. and Yu, R. 2020. Interpretable models do not compromise accuracy or fairness in predicting college success. In Proceedings of the Seventh ACM Conference on Learning @ Scale. L@S 2020. Association for Computing Machinery, New York, NY, USA, 413–416.
- Lundberg, S. M. and Lee, S.-I. 2017. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems, U. von Luxburg, I. Guyon, S. Bengio, H. Wallach, and R. Fergus, Eds. NeurIPS 2017, vol. 30. Curran Associates Inc., Red Hook, NY, 4768–4777.
- Macfadyen, L. P. and Dawson, S. 2010. Mining LMS data to develop an “early warning system” for educators: A proof of concept. Computers & Education 54, 2, 588–599.
- Mahzoon, M. J., Maher, M. L., Eltayeby, O., Dou, W., and Grace, K. 2018. A sequence data model for analyzing temporal patterns of student data. Journal of Learning Analytics 5, 1, 55–74.
- Mehrabi, N., Morstatter, F., Saxena, N., Lerman, K., and Galstyan, A. 2021. A survey on bias and fairness in machine learning. ACM Computing Surveys 54, 6 (jul), 1–35.
- O’Connell, K. A., Wostl, E., Crosslin, M., Berry, T. L., and Grover, J. P. 2018. Student ability best predicts final grade in a college algebra course. Journal of Learning Analytics 5, 3, 167–181.
- Paquette, L., Ocumpaugh, J., Li, Z., Andres, A., and Baker, R. 2020. Who’s learning? using demographics in EDM research. Journal of Educational Data Mining 12, 3, 1–30.
- Pascarella, E. T. and Terenzini, P. T. 2005. How College Affects Students: A Third Decade of Research. Volume 2. Vol. 2. Jossey-Bass, Indianapolis, IN.
- Pickering, J., Calliotte, J., and McAuliffe, G. 1992. The effect of noncognitive factors on freshman academic performance and retention. Journal of the First-Year Experience & Students in Transition 4, 2, 7–30.
- Plak, S., Cornelisz, I., Meeter, M., and van Klaveren, C. 2022. Early warning systems for more effective student counselling in higher education: Evidence from a dutch field experiment. Higher Education Quarterly 76, 1, 131–152.
- Sclater, N., Peasgood, A., and Mullan, J. 2016. Learning analytics in higher education: A review of UK and international practice. Tech. rep., JISC.
- Simons, J. M. 2011. A national study of student early alert models at four-year institutions of higher education. Ph.D. thesis, Arkansas State University. UMI Order Number: AAT 8506171.
- Tinto, V. 2012. Leaving college: Rethinking the causes and cures of student attrition, 2nd Edition. University of Chicago press.
- Trevisan, V. 2022. Using shap values to explain how your machine learning model works. https://towardsdatascience.com/using-shap-values-to-explain-how-your-machine-learning-model-works-732b3f40e137. Accessed: 11-22-2022.
- Tyton Partners. 2022. Driving towards a degree: Closing outcome gaps through student supports. https://tytonpartners.com/driving-towards-a-degree-closing-outcome-gaps-through-student-supports/ Accessed: 11-22-2022.
- Von Hippel, P. T. and Hofflinger, A. 2021. The data revolution comes to higher education: identifying students at risk of dropout in chile. Journal of Higher Education Policy and Management 43, 1, 2–23.
- Yu, R., Lee, H., and Kizilcec, R. F. 2021. Should college dropout prediction models include protected attributes? In Proceedings of the Eighth ACM Conference on Learning @ Scale. L@S 2021. Association for Computing Machinery, New York, NY, USA, 91–100.
- Yu, R., Li, Q., Fischer, C., Doroudi, S., and Xu, D. 2020. Towards accurate and fair prediction of college success: Evaluating different sources of student data. In Proceedings of the 13th International Conference on Educational Data Mining, A. N. Rafferty, J. Whitehill, V. Cavalli-Sforza, and C. Romero, Eds. EDM 2020. International Educational Data Mining Society, 292–301.
1In Japan, the academic year starts in April and ends in March.