Abstract
Bayesian Knowledge Tracing (BKT) is a popular interpretable computational model in the educational mining community that can infer a student’s knowledge state and predict future performance based on practice history, enabling tutoring systems to adaptively select exercises to match the student’s competency level. Existing BKT implementations do not scale to large datasets and are difficult to extend and improve in terms of prediction accuracy. On the other hand, uninterpretable neural network (NN) student models, such as Deep Knowledge Tracing, enjoy the speed and modeling flexibility of popular computational frameworks (e.g., PyTorch, Tensorflow, etc.), making them easy to develop and extend. To bridge this gap, we develop a collection of BKT recurrent neural network (RNN) cells that are much faster than brute-force implementations and are within an order of magnitude of a fast, fine-tuned but inflexible C++ implementation. We leverage our implementation’s modeling flexibility to create two novel extensions of BKT that significantly boost its performance. The first merges item response theory (IRT) and BKT by modeling multidimensional problem difficulties and student abilities without fitting student-specific parameters, allowing the model to easily generalize to new students in a principled way. The second extension discovers the discrete assignment matrix of problems to knowledge components (KCs) via stochastic neural network techniques and supports further guidance via problem input features and an auxiliary loss objective. Both extensions are learned in an end-to-end fashion; that is, problem difficulties, student abilities, and assignments to knowledge components are jointly learned with BKT parameters. In synthetic experiments, the skill discovery model can partially recover the true generating problem-KC assignment matrix while achieving high accuracy, even in some cases where the true KCs are structured unfavorably (interleaving sequences). On a real dataset where problem content is available, the skill discovery model matches BKT with expert-provided skills, despite using fewer KCs. On seven out of eight real-world datasets, our novel extensions achieve prediction performance that is within 0.04 AUC-ROC points of state-of-the-art models. We conclude by showing visualizations of the parameters and inferences to demonstrate the interpretability of our BKT RNN models on a real-life dataset.Keywords
1. Introduction
It is well-known that one-on-one tutoring is superior to traditional classroom instruction (Bloom, 1984) but the obvious impracticality of assigning a tutor to every student has made intelligent tutoring systems (ITS) a viable and cheaper alternative to individualized tutoring. ITS show a series of exercises for students to practice and are often equipped with extra features such as video explanations, adaptive hints, and even game-like mechanics. Such systems also enjoy an important advantage over traditional instruction: they log all the interactions with the student, providing a wealth of fine-grained data for analysis. Good tutoring systems adapt to the student’s performance; they provide exercises that are matched to the student’s skill level—not too easy nor too hard.
This adaptation requires a computational model of the student’s knowledge that can predict their performance on any given exercise. Research into student performance models has a long history and has produced models that capture different aspects of performance, such as the temporal dynamics of learning and forgetting (Corbett and Anderson, 1994, Pavlik et al., 2009, Pelánek, 2014), or the interaction between problem difficulty and student ability (Reckase, 1979, Ravand and Robitzsch, 2018, Finch and French, 2018).
One of the most popular temporal models of learning is Bayesian Knowledge Tracing (BKT) (Corbett and Anderson, 1994) which assumes that a student has a latent binary knowledge state representing whether they’ve learned the knowledge component (KC) or not. Broadly speaking, KCs are pieces of knowledge, skills, concepts, principles, or facets that students need to solve a problem (Koedinger et al., 2012) (e.g. if you need to solve an equation, you need to know how to add, subtract, and multiply). Throughout this work, we use KC and skill interchangeably. BKT assumes that KCs are independent: performance on one KC does not inform performance about another. State space models like BKT are attractive because they offer a clear cognitive story of how student answers are generated and because they naturally support post hoc state smoothing of the knowledge states, where the estimate of what the student knew at time \(t\) can be refined based on performance from previous and subsequent trials.
Compared to BKT, neural network (NN) (Goodfellow et al., 2016) models have attained state-of-the-art performance on benchmark educational datasets (Piech et al., 2015, Zhang et al., 2017, Gervet et al., 2020, Tsutsumi et al., 2021). NN models are attractive because of modeling flexibility: all that is required is a forward model of computation and the difficult task of learning and running on parallel processing hardware is left to the underlying computational framework (PyTorch, Tensorflow, etc.). The performance boost of NN models comes at the cost of interpretability as these models are either fully or partially uninterpretable.
We define interpretability from a machine learning perspective, which is the ability to understand the causes of a model’s decision or predictions (as suggested by Molnar (2022)). NN models often use distributed representations whose contributions to the final prediction are difficult to pinpoint. For example, in the well-known Deep Knowledge Tracing (DKT) model (Piech et al., 2015), it is unclear how previous practice history, KC features, and hidden state influence the predictions of the model. BKT on the other hand, has a handful of well-defined parameters (as we will see shortly) that interact with each other in a clear way that a human could grasp. As a result, one can easily understand how BKT’s predictions will change in response to a change in a parameter or the hidden state of the model.
We have identified three main issues that, if implemented in BKT, could reduce its disadvantage to NN models while maintaining interpretability at the same time. The first issue is unidimensional modeling of students and the inability to generalize to new students. As stated previously, BKT treats each KC independently so the student’s performance on one KC does not inform their performance on another. Extensions were developed to fix this by assuming, amongst other things, that the student has an overall ability level that influences performance on all KCs (Khajah et al., 2014, Gonzalez-Brenes et al., 2014, Pelánek, 2017). These extensions improve performance, but they fail to generalize to new students in a principled way (other than computationally expensive Bayesian implementations), with some implementations simply assuming that a new student would have an average ability level based on the training set. Moreover, to our knowledge, there are no BKT extensions that support multidimensional student abilities (e.g., to model students that learn quickly but forget slowly or vice versa), which recent literature showed can improve the performance of opaque NN models (Tsutsumi et al., 2021). The second issue is that BKT needs expert-provided problem-KC assignments. BKT requires problems to be annotated with the KCs required to solve them. Most existing BKT implementations assume that the problem-KC assignment matrix is given a priori. This is quite limiting as the expert-provided assignments require extra data collection and may not be accurate. One previous BKT extension can discover the problem-KC assignment matrix (Lindsey et al., 2014), but it is computationally demanding and inflexible. Finally, BKT does not leverage problem input features such as problem text when making predictions. Such features can provide vital information about the problems’ difficulty and relationship to other problems, both of which can improve prediction performance.
Unfortunately, BKT’s implementation liabilities limit its appeal to researchers wishing to extend BKT and reduce its performance deficit to NN models. The model has five free parameters which are commonly trained via brute-force grid-search algorithms (Martori et al., 2015) that are inflexible and unscalable, and expectation maximization (EM) and gradient descent algorithms (Pardos and Heffernan, 2010, Yudelson, 2022) that are scalable but inflexible. None of the BKT implementations leverage the parallel processing capabilities of modern Graphics Processing Units (GPUs).
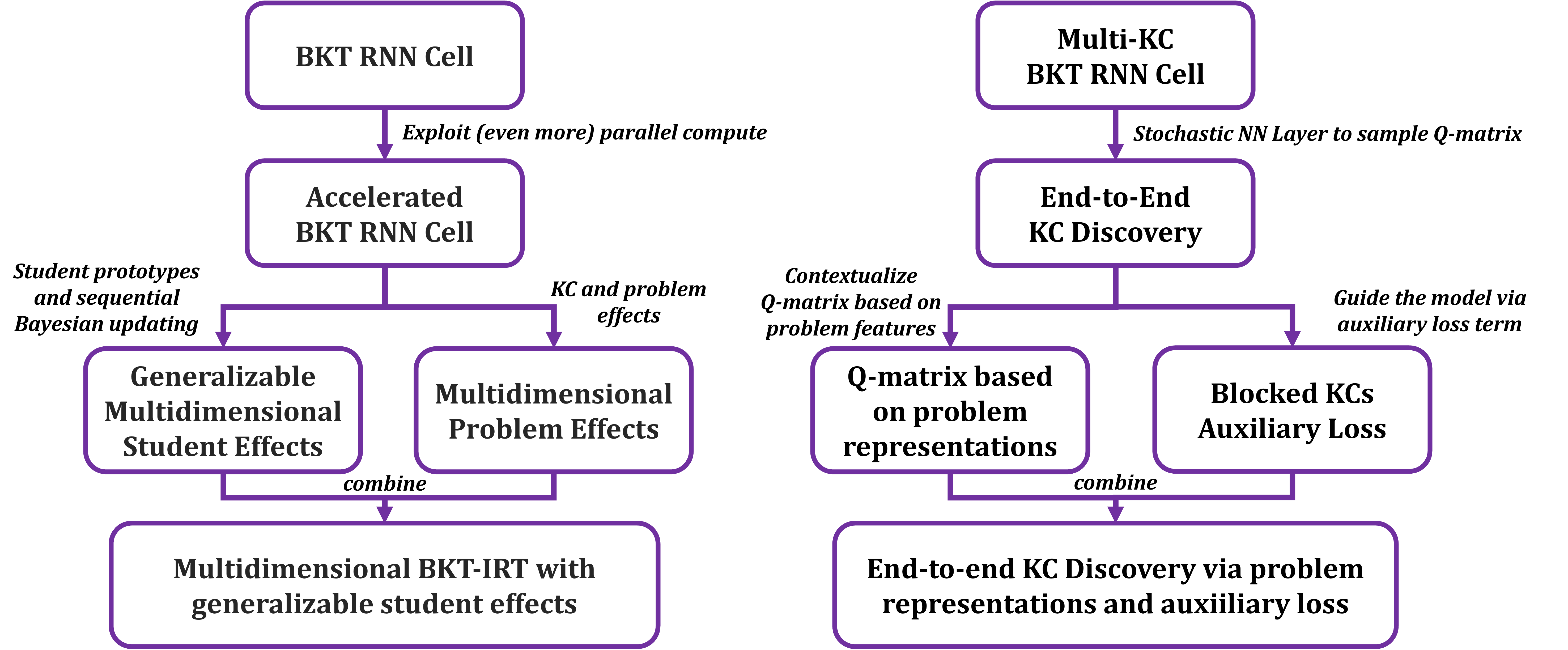
In this paper, we make three contributions (Figure 1) that solve the above-mentioned issues with BKT:
- Fast and flexible BKT implementation: we implement BKT as a fast recurrent neural network (RNN) layer in PyTorch (Paszke et al., 2019) with optimizations specific to GPUs. PyTorch supports automatic differentiation and several stochastic gradient descent algorithms, making it easy to implement complex extensions to BKT, much in the same way as black box uninterpretable models such as DKT (Piech et al., 2015). This flexibility is demonstrated by our next two novel contributions.
- BKT with multidimensional generalizable problem and student effects: this model fixes inaccurate problem-KC assignments via multidimensional student and problem effects which are used to contextualize BKT parameters. The abilities of new students are inferred via a principled sequential Bayesian mechanism.
- Skill discovery BKT model with problem features: this extension discovers the mapping from problems to KCs such that they are inline with BKT’s assumption that all problems within a KC have the same difficulty. The model is further extended to use problem input features to contextualize KC membership probabilities, and to use an auxiliary loss term that encourages KC assignments that result in blocked KC sequences (e.g., KC 1, 1, 2, 2, 3, 3, etc.). We use two metrics to quantitatively measure the agreement between discovered and true KC assignments, both when KCs are blocked and interleaved. Furthermore, we demonstrate that real-world datasets are not strictly interleaving or blocking and so the performance of skill discovery is evaluated under shadow versions of real-world datasets with different KC ordering patterns.
Our basic BKT RNN implementation is substantially faster than brute-force BKT implementations and is within an order of magnitude of a fine-tuned C++ BKT implementation. The GPU-accelerated variant of BKT RNN exploits the special properties of BKT to reduce execution time, and it matches the fine-tuned C++ BKT model on large datasets. BKT with generalizable multidimensional student and problem effects matches the uninterpretable DKT model in some real-world datasets or is within a few percentage points of it. On some datasets, multidimensional student abilities clearly improve upon unidimensional ones. The skill discovery model can partially recover the true problem-KC assignment matrix in synthetic datasets if provided with problem representations. On almost all real-world datasets, it performs as well as BKT with problem effects. On one real-world dataset with problem features, the model matches the performance of BKT with expert-provided skills.
2. Background and Literature Review
An example of an educational dataset used to train computational models in this paper is shown in Table 1. Every student attempts a series of trials, and every trial is associated with a problem, KC, and whether the student answered it correctly or not. Typical educational datasets contain more information such as the start time, number of attempts, and so on, but this paper only looks at the columns illustrated in Table 1.
The modeling task is to then estimate the following conditional probability: \begin {equation} \label {eq1} p(y_{t}=1 \mid \mathbf {y}_{1:t-1},\mathbf {x}_{1:t}) \end {equation} where \(y_t\) is the correctness at time \(t\), \(\boldsymbol {y}_{1:t}\) is the correctness of all trials from 1 up to and including \(t\), and \(\mathbf {x}_{1:t}\) are all the other information associated with trials 1 up to \(t\) (KCs, problems, etc.). For example, we could ask what is the probability that student S1 answers trial 3 correctly, given all information about trials 1 and 2. Modeling Equation 1 accurately can enable a more intelligent selection of exercises for the student to practice; if the software accurately predicts that the student will solve a problem correctly, it can select a problem that is more challenging to keep the student in Vygotsky’s zone of proximal development, where the student can learn a skill with some guidance. Models that estimate the conditional probability in Equation 1 can broadly be categorized into temporal and student-item models.
| Trial | Student | Problem | Problem ID | KC | Correct |
|---|---|---|---|---|---|
| 1 | S1 | \(3+4\) | 1 | Addition | Yes |
| 2 | S1 | \(\frac {3}{4}\) | 2 | Fractions | No |
| 3 | S1 | \(5 + x = 10\) | 3 | Equation Solving | No |
| 1 | S2 | \(10 \times 8\) | 4 | Multiplication | Yes |
| 2 | S2 | \(\frac {3}{4}\) | 2 | Fractions | Yes |
| 3 | S2 | \(7 + x = 3\) | 5 | Equation Solving | Yes |
| ... | ... | ... |
Temporal models explicitly assume that the student’s knowledge evolves over time, thereby allowing for learning and forgetting effects. The most prominent of such models is Bayesian Knowledge Tracing (BKT) (Corbett and Anderson, 1994) which is a simple state space model where the hidden state represents whether the student knows the KC or not. If the student knows the KC, they may “slip” with some probability, and if the student doesn’t know the KC, they may “guess” with some probability. The student has a probability of learning the KC at any given time step, and they never forget the KC once it is learned. The no-forgetting constraint is too restrictive on real-life datasets, and it has been shown that removing it improves performance over standard BKT (Khajah et al., 2016). Another temporal model is the exponential moving average (EMA) (Pelánek and Řihák, 2017), where the probability of a correct response is a weighted average of recent trials, with trial weights exponentially decreasing over time. The downside of both models, however, is that they are fit on a KC-by-KC basis, so there is one model per KC, and relationships amongst answers on different KCs are not considered. Furthermore, neither BKT nor EMA model student abilities or specific problem difficulties.
Unlike temporal models, student-item models assume that the probability of answering correctly is a function of some set of features of the trial: the student, the problem, the KC, etc. (item and problem are used interchangeably throughout this paper). Perhaps one of the earliest examples of such models are Item Response Theory (IRT) models (Boeck and Wilson, 2004, Finch and French, 2018, Reckase, 1979) which dissociate student ability from problem difficulty. IRT assumes that the probability of answering correctly is a function of the student’s ability and the problem’s difficulty, so a correct answer may be due to a competent student or an easy problem. Multidimensional extensions to IRT (Yao and Schwarz, 2006, Reckase, 2009, Ackerman, 1989) characterize students and problems by more than one dimension, unlocking greater prediction performance. Regardless of dimensionality, standard non-Bayesian formulations of IRT cannot generalize to new students because they do not make distributional prior assumptions on the student ability parameters. IRT models are also static in the sense that they assume that a student’s knowledge state is fixed, so they do not take prior practice history into account when making a prediction for a new trial. In other words, standard IRT assumes no learning effects. Wilson et al. (2016) proposed a temporal extension to IRT where a student has one unidimensional global ability parameter that evolves over time, unlike BKT which assigns a binary knowledge state per skill. The model places a hierarchical prior over problem difficulties, with problems belonging to the same KC sharing the same prior. Compared to Wilson’s approach, BKT is more useful because it provides a finer-grained picture of the student’s knowledge (i.e., what skills the student knows).
Logistic regression (LR) models, such as Additive-Factors Models (AFM) and DASH (Lindsey et al., 2014), have also been used to model student performance. Unlike state space models, LR models do not assume the existence of a hidden state; instead, they explicitly use prior observations to calculate the probability of a correct answer. In AFM, that probability depends on the student’s ability, the problem’s difficulty, and previous successes and failures on each KC associated with the problem, regardless of how recent those successes and failures were. DASH addresses this limitation by counting successes and failures within expanding time windows (the past hour, day, week, month, etc.). While models like DASH consider the temporal distribution of practice as well as student and problem effects, they do not provide an intuitive generative story about how the student answers exercises. For this reason, state-space models like BKT remain attractive because they offer a clear cognitive story about the student’s performance (e.g., the student answered the trial correctly because they knew the KC with probability 90% at that time).
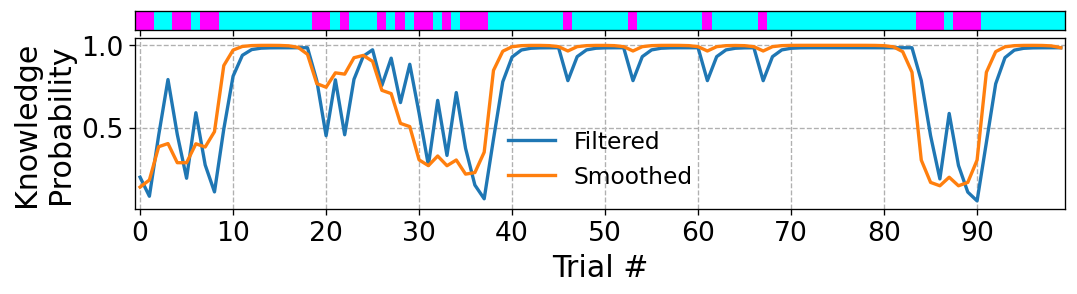
Indeed, one of the advantages of state-space models is their smoothing ability, in which the posterior marginal distribution over the knowledge state at any given time step can be estimated by using previous and subsequent trials. In a predictive regression model, such as AFM and DASH, the student’s “knowledge state” is inferred based only on past trials. So if one was interested in using such a model for smoothing, they would have to modify the model to account for future observations. With state space models like BKT, one model can be used both for prediction and smoothing. Figure 2 shows a sample observation sequence (top), and the estimated filtered and smoothed probability that the student knows the skill (bottom). Filtered probabilities are based on previous trials while smoothed probabilities are based on all trials (one BKT model was used to generate both estimates). The smoothed estimates are especially useful for post hoc diagnosis of student learning. For instance, we see that the orange curve in the Figure is less “reactive” than the blue curve as the latter tends to sharply change value when an unexpected observation occurs, which may not be realistic.
BKT and IRT models were merged such that guessing and slipping probabilities of BKT are modulated based on the problem’s difficulty and the student’s ability (Khajah et al., 2014, Gonzalez-Brenes et al., 2014). The method proposed by Khajah et al. (2014) also has the advantage of being able to generalize to new students in a principled way due to its Bayesian nature. Both approaches outperformed BKT and IRT, showing that temporal and student-item effects are complementary. Another approach to leveraging problem information is the Weighted Chinese Restaurant Process (WCRP) model (Lindsey et al., 2014) which, instead of modulating BKT’s parameters via problem features, finds better mappings from problems to KCs using a non-parametric Bayesian approach. In other words, WCRP finds a problem-KC mapping that better suits BKT’s assumptions than what is provided by experts. Results on several datasets showed that WCRP finds better KC assignments than the experts and outperforms BKT. But, being a Bayesian model, WCRP requires extensive computational resources to run. Additionally, modifying the observation model of WCRP is not trivial due to the complexity of the mathematics involved in constructing the Markov-Chain-Monte-Carlo (MCMC) sampler, making it difficult to inject additional features into the model. An alternative popular method for skill discovery is Learning Factors Analysis (LFA) (Cen et al., 2006), which uses AFM to explore possible KC splits that would increase AFM’s prediction accuracy. LFA starts from a given problem-KC matrix and searches through the combinatorial space of pre-defined factors along which KCs could be split. In one study, a BKT-powered intelligent tutoring system that used the problem-KC matrix generated by LFA was found to be superior in terms of student learning outcomes than BKT with the initial expert-provided matrix (Liu and Koedinger, 2017). But LFA still requires manually pre-defining the space of possible KC-splitting factors and the matrices it discovers are not guaranteed to be optimal for BKT because the underlying model being optimized is AFM, not BKT.
A recurrent neural network model (RNN) known as Deep Knowledge Tracing (DKT) was proposed as a replacement for classical BKT (Piech et al., 2015). The model used a vanilla RNN architecture known as Long-Short-Term-Memory (LSTM) and outperformed BKT on all the datasets it was tested on. DKT, by virtue of being an RNN, is easy to integrate with other neural network modules, such as those that learn rich representations from raw problem input (e.g., problem text or image). But, like most NN architectures, DKT is not interpretable; it is a black box whose predictions cannot be explained, unlike simpler models like BKT and IRT. Subsequent investigations of DKT found that its advantage was primarily due to different evaluation metrics used for BKT and DKT and that the complex temporal dynamics supported by DKT are not necessary to achieve good predictive performance (Khajah et al., 2016, Montero et al., 2018). Since DKT, several neural network black box models have been developed (Zhang et al., 2017, Ghosh et al., 2020, Tsutsumi et al., 2021) that use RNNs, Transformers, and Dynamic Key-Value Memory Networks (DKVMN) (Vaswani et al., 2017) (For an overview, please refer to Gervet et al. (2020)).
Some of these extensions have attempted to provide partial interpretability, such as Deep-IRT (Yeung, 2019, Tsutsumi et al., 2021) and context-aware knowledge tracing (Ghosh et al., 2020). Deep-IRT connects a DKVMN to two shallow networks: a student ability network and a problem difficulty network. The outputs of the latter two networks are combined via IRT to produce the final prediction. Ghosh et al. (2020) uses IRT to create regularized raw embeddings of questions and question-response pairs. The embeddings are fed into a transformer to compute context-aware embeddings that consider the previous practice history (using a monotonically decaying attention mechanism to model forgetting). Finally, the context-aware embeddings are fed into another transformer to estimate the student’s knowledge state before making the final prediction. The problem with both prior works is they use embeddings whose individual values cannot be succinctly described in terms of how they affect model predictions. For example, in Deep-IRT, it is not possible to describe how the 5th, 6th, or 41st value in a KC’s embedding vector contributes to the prediction, or what it means in an educational context (is it related to guessing, slipping, or some other feature?) This lack of interpretability is because neural networks in general are good at learning distributed representations of inputs, which are difficult to dissect and understand.
In this work, we implement BKT as an RNN to reap the benefits of modeling flexibility and parallel computing while retaining the interpretability of the model. We showcase the advantages of this approach by creating two main novel extensions of the model that improve performance beyond vanilla BKT: multidimensional BKT+IRT with generalizable student abilities, and a BKT model that supports end-to-end learning of the problem-KC assignment matrix.
3. Methods
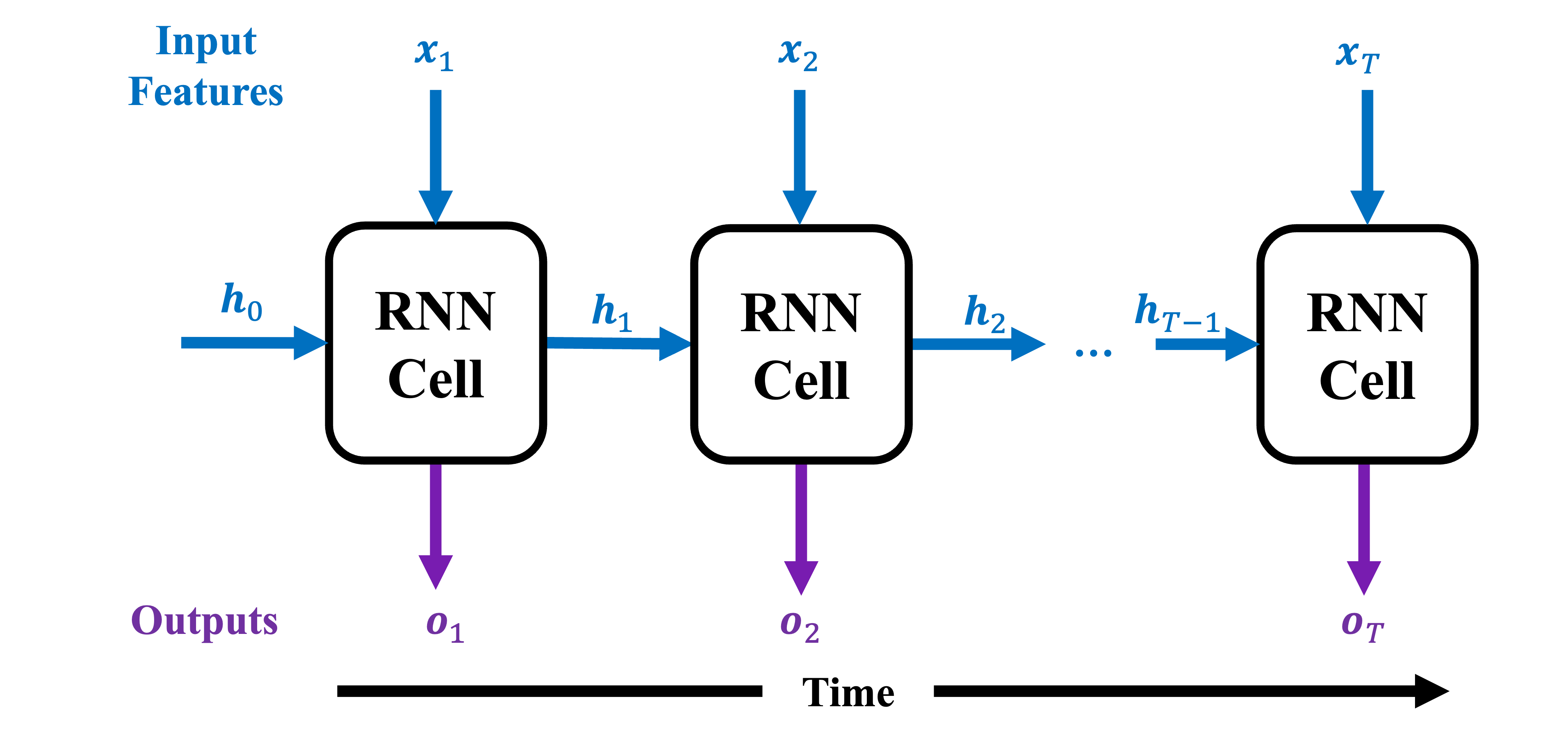
All models developed here are implemented as RNNs with specialized cell dynamics. RNNs are neural networks that model time-series data by updating an internal state over time via a feedback loop. Since neural networks are directed acyclic graphs that do not allow feedback loops, RNNs are implemented by unrolling the dynamics over a fixed number of time steps. They are generally defined as follows: \begin {align} \boldsymbol {h}_{t} & =f(\boldsymbol {h}_{t-1},\boldsymbol {x}_{t})\label {eq:rnn_statespace}\\ \boldsymbol {o}_{t} & =g(\boldsymbol {h}_{t}) \end {align}
where \(f\) and \(g\) are some parameterized functions, and \(\boldsymbol {x}_t\), \(\boldsymbol {h}_t\), \(\boldsymbol {o}_t\) are the input, hidden state, and output at time \(t\), respectively. At each time step, the cell accepts input features \(\boldsymbol {x}_t\) and the previous state \(\boldsymbol {h}_{t-1}\) and emits the new state \(\boldsymbol {h}_t\) and output \(\boldsymbol {o}_t\). Figure 1 graphically illustrates this process over time (note that all RNN cells in the Figure share the same free parameters). The differences amongst RNN architectures are due to different choices of \(f\) and \(g\) above. In this paper, we propose \(f\) and \(g\) such that they exactly implement the dynamics of BKT.
3.1. Bayesian Knowledge Tracing as an RNN
Technically, BKT is a Hidden Markov Model (HMM) (Jurafsky and Martin, 2009) with two hidden states and two outputs. One BKT model is fit per KC in the dataset, so if a dataset has \(N\) KCs, then \(N\) BKT models would be required. Mathematically, BKT is defined as follows: \begin {align} p(y_{t}=1 \mid s_{t}) & =\begin {cases} p_{G} & s_{t}=0\\ 1-p_{S} & s_{t}=1 \label {eq:bktobseq} \end {cases}\\ p(s_{t}=1 \mid s_{t-1}) & =\begin {cases} p_{L} & s_{t-1}=0\\ 1-p_{F} & s_{t-1}=1 \label {eq:bktstateeq} \end {cases}\\ p(s_{1}=1) & =p_{I} \label {eq:bktinitstate} \end {align}
where \(s_t\) is the latent binary knowledge state, \(y_t\) is the observation (correctness) at time \(t\), and \(p_G\), \(p_S\), \(p_L\), \(p_F\), and \(p_{I}\) are the guessing, slipping, learning, forgetting, and initial knowledge probabilities, respectively. The student answers correctly with probability \(p_G\) if they don’t know the KC (\(s_t = 0\)) or \(1-p_S\) if they do know the KC (\(s_t = 1\)). The probability that the student learns or forgets the KC when going from time \(t-1\) to \(t\) is \(p_L\) and \(p_F\), respectively. Finally, the probability that the student starts out knowing the KC is \(p_{I}\).
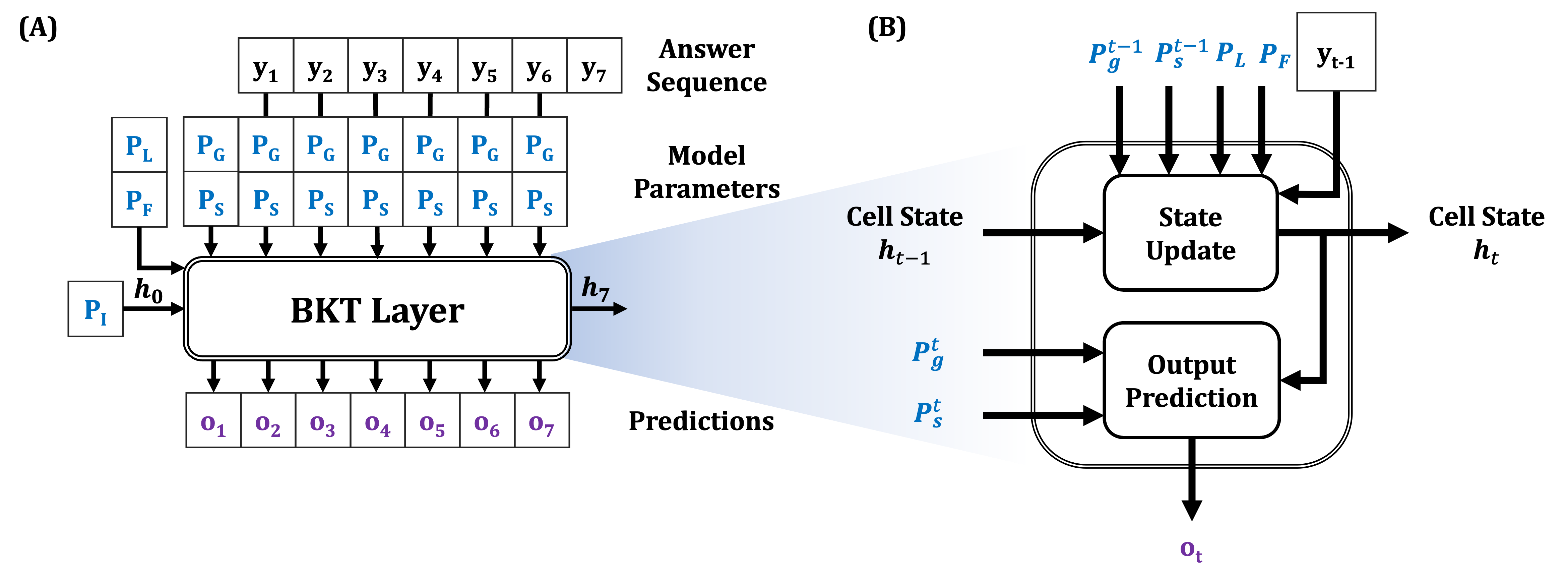
Given these probabilities, determining the probability of knowing the KC at time \(t\) requires examining all the possible trajectories of latent states that lead the student to knowing the KC at time \(t\). The forward algorithm (Jurafsky and Martin, 2009), which computes the likelihood of a sequence under the model, efficiently solves this problem via dynamic programming. This algorithm is fully differentiable with respect to the parameters of the model. Therefore, an RNN implementation of the forward algorithm will automatically compute the gradients necessary for learning BKT parameters. Figure 4A illustrates the high-level architecture of the BKT RNN layer for one KC. The inputs to the BKT layer are the answer sequence (\(y_t\)), the initial, learning, and forgetting probabilities (\(p_I\), \(p_L\), \(p_F\)), and the guessing and forgetting probabilities (\(p_G\), \(p_F\)). The output is the predicted probability of a correct answer, given prior answers as well as the next state (\(\boldsymbol {h}_t\)). Supplying BKT’s parameters separately as input to the BKT layer makes it trivial to integrate the model with other NN modules (later, we will see examples of this). In Figure 4B, the details of a BKT RNN cell are shown. Here, the cell state \(h_t(j)\) is the probability of observing all observations up to \(t-1\) and ending up at knowledge state \(j \in \{0, 1\}\) at time \(t\). This state is updated as follows: \begin {equation} h_{t}(j)=P(s_{t}=j,y_{1}...y_{t-1})=\sum _{s_{t-1}=0}^{M-1}\underbracket {P(s_{t}\mid s_{t-1})}_{\text {state transition}}\underbracket {P(y_{t-1}\mid s_{t-1})}_{\text {output}}h_{t-1}(s_{t-1})\label {eq:hmmupdate} \end {equation} where \(M = 2\) is the number of possible knowledge states and the state transition and output probabilities are as shown in Equations \eqref{eq:bktstateeq} and \eqref{eq:bktobseq}, respectively. Given the updated state, the probability of the output at the current time step can be computed: \begin {equation} o_{t}(i)=P(y_{t}=i\mid \mathbf {y}_{1:t-1})\propto \sum _{s_t=0}^{M-1}P(y_{t}\mid s_{t})h_{t}(s_t)\label {eq:hmmpredict} \end {equation} This equation states that the final output probability is a weighted average of the output probability under every possible knowledge state, with the weight of knowledge state \(s_t\) given by \(h_t(s_t)\).
The training objective of the model is the usual binary cross-entropy, which is the negative log probability of the data under the model: \begin {equation} \mathcal {L}_{BCE}(\mathcal {D})=-\sum _{s=1}^{S}\sum _{t=1}^{N_{s}}y_{st}\text {log}\hat {y}_{st}+(1-y_{st})\text {log}(1-\hat {y}_{st}) \end {equation} where \(\mathcal {D}\) is the training dataset, \(S\) is the number of students, \(N_s\) is the length of trial sequence for student \(s\), \(y_{st}\) is the observation at time \(t\) from student \(s\), and \(\hat {y}_{st}\) is the prediction of the model.
3.1.1. Accelerating BKT RNN
One of the reasons behind the recent success of large language models is the transformer architecture (Vaswani et al., 2017), whose computations are especially suited for parallel-compute hardware such as graphical processing units. The transformer’s match to modern hardware made training on very large datasets feasible. We can therefore ask: can we apply the same computational philosophy of the transformer to accelerate training and inference in BKT RNNs? Specifically, can we process more trials in a sequence in parallel?
Note that Equations \eqref{eq:hmmpredict} and \eqref{eq:hmmupdate} process the input sequence one trial at a time, as with any RNN architecture. However, it turns out that the special properties of BKT allow us to practically process multiple trials at a time. To see this, recall that the probability of a sequence of \(N\) observations is: \begin {align} P(y_{1}...y_{N}) & =\sum _{\mathbf {s}}\underbracket {P(y_{1}...y_{t}|\mathbf {s})}_{\text {Likelihood of $\mathbf {s}$}}\underbracket {P(\mathbf {s})}_{\text {Prior on $\mathbf {s}$}}\\ & =\sum _{\mathbf {s}}\prod _{t=1}^{N}P(y_{t}|s_{t})P(s_{t}|s_{t-1}) \label {eq:brutehmm} \end {align}
The summation in the previous two equations is over all possible state-space trajectories \(\mathbf {s}\). Given a particular trajectory, computing the likelihood of the observations is trivial due to the independence structure of an HMM. Specifically, all observations are independent given the trajectory, and the prior on the trajectories just involves successively applying the transition probability of the HMM, hence the product term in Equation \eqref{eq:brutehmm}. The important point here is that products in outer summation can be computed in parallel as well as the terms within a product.
In BKT’s case, there are only two knowledge states so a sequence of \(N\) observations has \(2^N\) possible state space trajectories. Obviously, for longer sequences, it would be impractical to apply Equation \eqref{eq:brutehmm} directly, but we can combine the scalability of the forward algorithm with the parallelism of Equation \eqref{eq:brutehmm}. Specifically, the standard state update equation (Equation \eqref{eq:hmmupdate}) would be modified as follows: \begin {align} h_{t}(j) =P(s_{t}=j,y_{1}...y_{t-1}) &=\sum _{\mathbf {s}^{C}}P(y_{t-C:t-1}|\mathbf {s}^{C})P(s_{t-C+1}|s_{t-C})h_{t-C}(s_{t-C})\\ &= \sum _{\mathbf {s}^{C}}\left (\prod _{i=t-C}^{t-1}P(y_{i}|s_{i})\right )P(s_{t-C+1}|s_{t-C})h_{t-C}(s_{t-C}) \end {align}
Here, \(C\) is the stride or the number of trials that would be processed at one time, and \(\mathbf {s}_C\) are all state trajectories of length \(C\). When \(C = 1\), we recover the standard forward algorithm (Equation \eqref{eq:hmmupdate}). For a sensible choice of \(C\), such as between 5 and 7, this modification results in speed-ups over the standard forward algorithm when implemented on graphics processing units, as we’ll see in the results section.
3.2. Problem Effects and Generalizable Student Abilities
In standard BKT, performance on one KC does not inform performance on another. This is limiting because it does not model the fact that a student who does well on previous KCs is likely to do well on the next KC. One simple way of addressing this issue is to assume that a student has an unknown constant ability parameter that influences the probability of answering correctly (Khajah et al., 2014, Gonzalez-Brenes et al., 2014, Khajah et al., 2016) as follows: \begin {align} \text {logit}p_{G}&=\gamma _{k}+\theta _{u}\\\text {logit}p_{S}&=\psi _{k}-\theta _{u} \label {eq:bktabilities} \end {align}
where \(\theta _{u}\) is the ability of student \(u\), \(\gamma _{k}\) and \(\psi _{k}\) are offset parameters that behave like the probability of guessing and slipping on KC \(k\), respectively, and \(\text {logit}(x)=\text {log}\left (\frac {x}{1-x}\right )\). In the previous two equations, the greater the student’s ability, the higher the probability of guessing and the smaller the probability of slipping, and vice-versa. Because the same ability parameter \(\theta _u\) is used in both equations, the implication is that the student’s baseline probability of answering correctly (i.e., when \(\gamma _{k}\) and \(\psi _{k} = 0\)) is the same regardless of whether they know a KC or not. Strictly speaking, the student ability here characterizes their baseline variance in performance: when \(\theta _u \approx 0\), the baseline guessing and slipping probabilities will be close to 0.5 (maximum variance), but as \(| \theta _u | \rightarrow \infty \), the probabilities will be close to 0 or 1 (minimum variance), depending on the sign of \(\theta _u\). If \(\theta _{u}\) is always set to 0, we recover standard BKT. Note that the student’s ability should not be conflated with their knowledge of the KC. Rather, the student ability parameter transcends all KCs that the student practices, allowing information about the student’s performance on one KC to be used for predicting performance on another. For example, if the student does well on multiplication, that implies they have good general ability, which will transfer to other skills such as division. If the KCs were annotated properly such that they are fully independent to satisfy BKT’s assumptions, the student ability parameter would be unnecessary. However, on real life datasets, KCs are seldom annotated to satisfy BKT’s assumption.
Misannotation of KCs can also lead to varying problem difficulties within a single KC. To account for this, separate problem-specific guessing and slipping parameters can be used: \begin {align} \text {logit}p_{G} & =\gamma _{k}+\omega _{p}+\theta _{u}\label {eq:bktirt1}\\ \text {logit}p_{S} & =\psi _{k}+\sigma _{p}-\theta _{u} \label {eq:bktirt2} \end {align}
where \(\omega _{p}\) and \(\sigma _{p}\) are the guessing and slipping offsets for problem \(p\), respectively. This formulation assumes that the KC guessing and slipping probabilities are modulated by problem effects. The latter effects are initialized to 0 to encourage the model to focus on fitting the KC-specific parameters and to ensure that new problems have \(\omega _p = 0\) and \(\sigma _p = 0\) (potentially enabling better generalization to new problems). This approach can also be combined with L1 or L2 regularization to force problem effects to be close to zero, although we do not apply those techniques in this work. After applying Equations \eqref{eq:bktirt1} and \eqref{eq:bktirt2}, the BKT layer in Figure 4 can be used as is since it allows for the guessing and slipping probabilities to be different at each time step.
However, the above formulation has a problem: new students will not have ability estimates. Previous Bayesian approaches to this problem handle this in a principled way by drawing new ability samples from the posterior predictive distribution over student abilities (Khajah et al., 2014, Khajah et al., 2016). Inspired by these approaches, our approach discretizes the ability values and sequentially estimates the distribution over these values via Bayes rule. For a new student, the ability estimate will get progressively better as he or she solves more exercises. Let \(\theta _{u}\) be a random variable that takes one of \(V\) uniformly spaced levels on some interval \([a, b]\). The probability of the next observation is then: \begin {equation} P(y_{t}\mid \mathbf {y}_{1:t-1})\propto \sum _{\theta _{u}}\underbracket {P(y_{t}\mid \mathbf {y}_{1:t-1},\theta _{u})}_{\text {BKT prediction given $\theta _u$}}\underbracket {P(\theta _{u},\mathbf {y}_{1:t-1})}_{\text {weight of $\theta _u$}} \label {eq:bktabilitiespred} \end {equation} In other words, the probability of the next observation is proportional to a weighted average of \(V\) BKT models’ predictions, with each BKT model assuming a particular value of \(\theta _u\) for the student. The weight of each value of \(\theta _u\) is given by the joint distribution of \(\theta _u\) and all observations up to and including time \(t-1\): \begin {equation} P(\theta _{u},\mathbf {y}_{1:t-1})=\underbracket {P(y_{t-1} \mid \mathbf {y}_{1:t-2},\theta _{u})}_{\text {BKT prediction given $\theta _u$}}\underbracket {P(\theta _{u},\mathbf {y}_{1:t-2})}_{\text {Previous joint distrib.}} \label {eq:bktabilitiesupdate} \end {equation} A uniform prior distribution is assumed over student abilities, \(P(\theta _{u}) \propto 1\). We should re-emphasize that student abilities are assumed to be constant in this model. What changes is the model’s belief about the distribution over the abilities of the student, given their practice history.
Implementing generalizable ability inference can easily be done, provided that the answer sequence and predictions are appropriately pre- and post-processed, respectively (Figure 5). As is usual with BKT models, the answer sequence is split by KC. Each subsequence is fed into \(V\) BKT layers, with each layer assuming a different ability level (\(V = 3\) in the Figure). The predictions of all layers are then reassembled, creating \(V\) sequences corresponding to predictions of \(V\) BKT models. The sequential Bayesian update layer combines these sequences into the final prediction using Equations \eqref{eq:bktabilitiespred} and \eqref{eq:bktabilitiesupdate}. This complete model is called BKT+IRT because it merges BKT temporal dynamics with problem and student effects from IRT models.
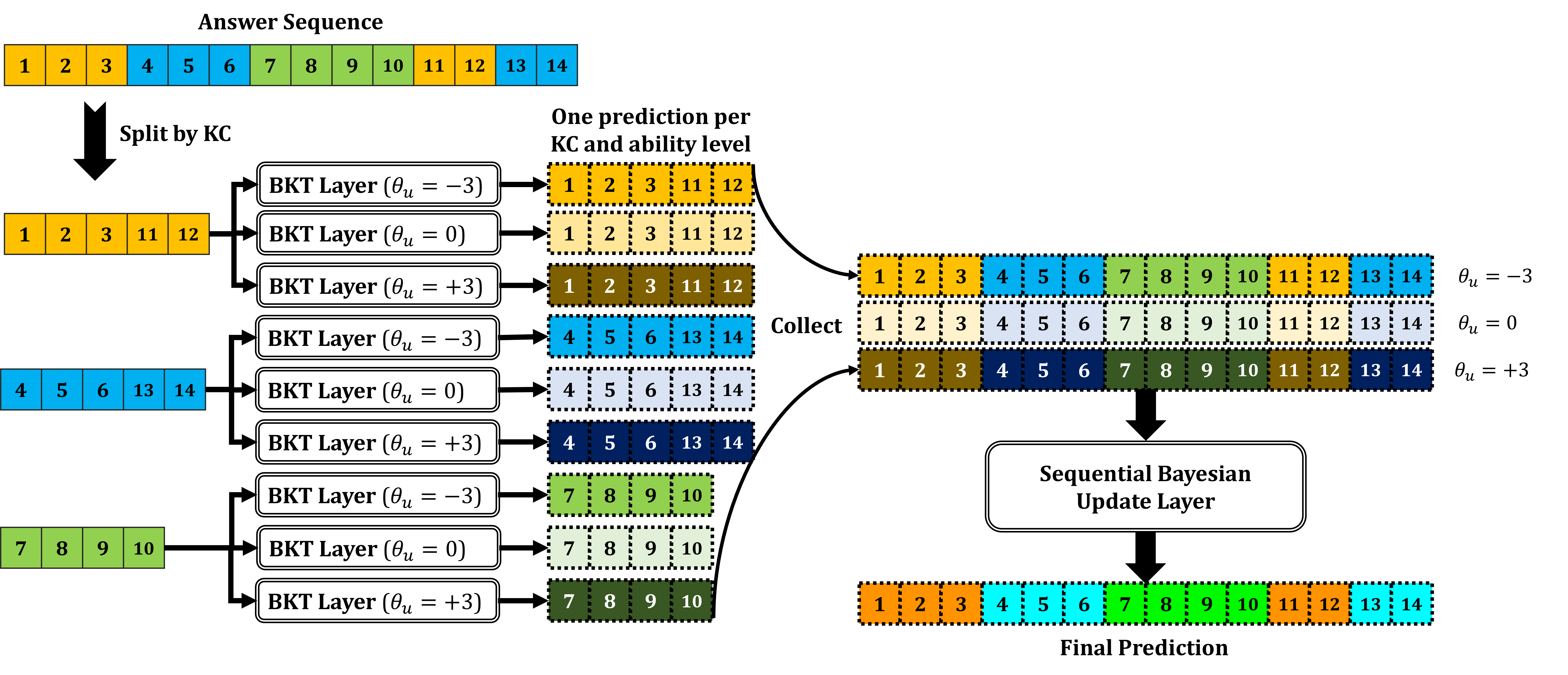
3.2.1. Multidimensional Abilities
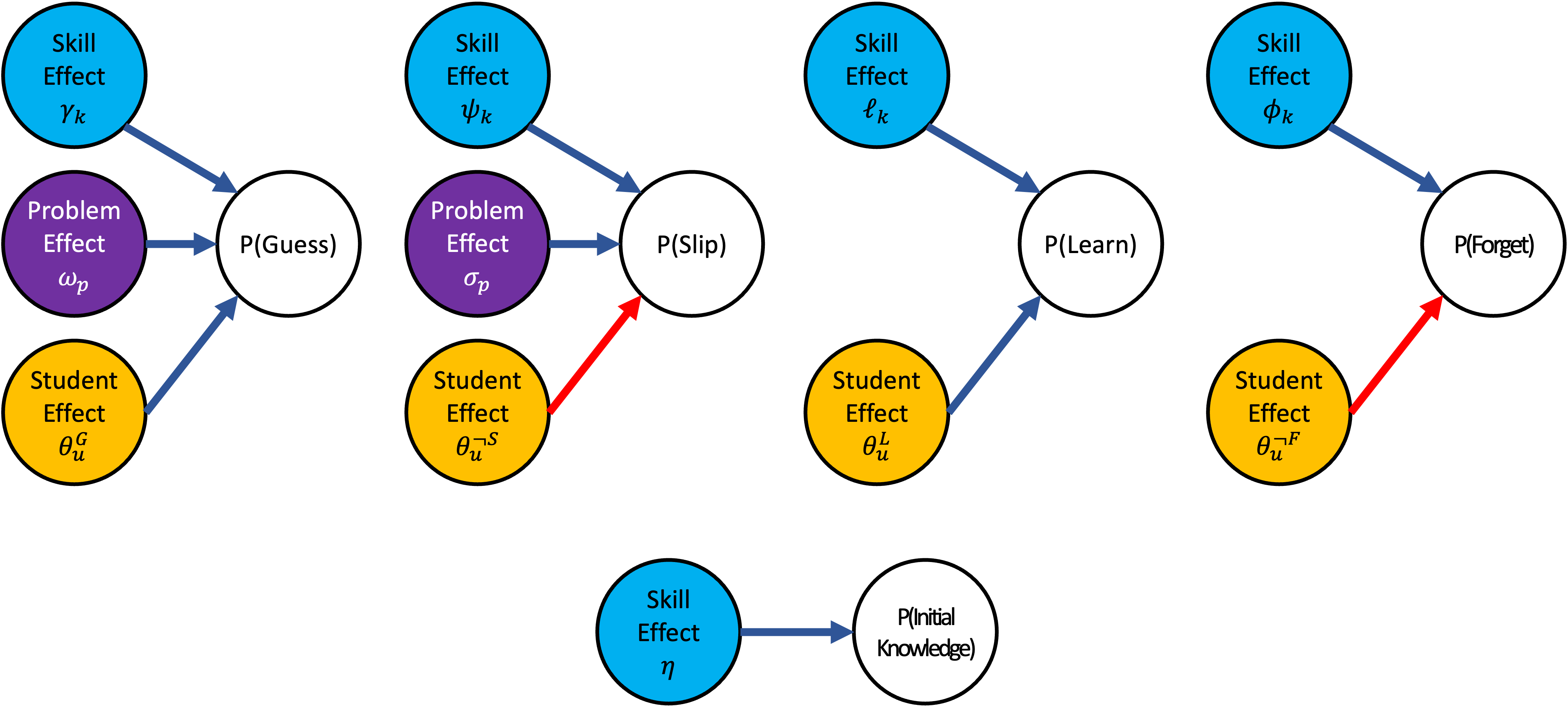
The student ability parameter in the previous section was used to modulate the guessing and slipping probabilities of BKT. However, one can imagine an extension whereby the ability of the student affects other parameters. For example, a student may learn slowly and forget slowly, or vice-versa. To support this, we can have four ability dimensions controlling the offsets on the guessing, slipping, learning, and forgetting probabilities: \begin {align} \text {logit}p_{L} & =\ell _{k}+\theta _{u}^{L}\label {eq:bktirt_pL}\\ \text {logit}p_{F} & =\phi _{k}-\theta _{u}^{\neg F}\label {eq:bktirt_pF}\\ \text {logit}p_{G} & =\gamma _{k}+\omega _{p}+\theta _{u}^{G}\label {eq:bktirt_pG}\\ \text {logit}p_{S} & =\psi _{k}+\sigma _{p}-\theta _{u}^{\neg S}\label {eq:bktirt_pS} \end {align}
where \(\ell _{k}\) and \(\phi _{k}\) are the learning and forgetting offsets for KC \(k\), respectively, and \(\mathbf {\theta }_u = [\theta _u^L, \theta _u^{\neg F}, \theta _u^G, \theta _u^{\neg S}]\) are the multidimensional student learning, not forgetting, guessing, and not slipping abilities, respectively. Figure 6 graphically illustrates the previous Equations. Dark blue edges correspond to proportional relationships (e.g., as the skill guessing offset \(\gamma _k\) increases, the probability of guessing on that skill increases). Red edges correspond to inversely proportional relationships (e.g., as the student’s no-slipping ability \(\theta _{u}^{\neg S}\) increases, the probability of slipping decreases).
An important point to note here is that, under BKT, the student’s knowledge profile is multidimensional because the student has a knowledge state per skill. Our multidimensional extension to BKT deals with the student’s global ability. Previous approaches treated this only as a scalar that influences the guessing and slipping probabilities of each skill (Khajah et al., 2014, Gonzalez-Brenes et al., 2014) or as a time-changing ability parameter in IRT (Wilson et al., 2016). In our multidimensional extension to BKT+IRT, the student’s global ability is multifaceted. In other words, the student’s knowledge profile and global ability are both multidimensional.
A naive implementation of this model is to enumerate all possible combinations of \(\mathbf {\theta }_u\) (just as the ability values in the previous section were enumerated), but that would quickly become computationally infeasible. Instead, we propose learnable student prototypes to enable the model to learn the common types of students from the training dataset and apply the sequential Bayesian update layer on those types, as in the previous section. Specifically, let \(\mathbf {\Theta } \in \mathbb {R}^{R \times 4}\) be a learnable student prototype matrix with \(R\) prototypes. The columns correspond to the student’s learning, not forgetting, guessing, and not slipping offsets. The \(R\) ability levels are used to contextualize those probabilities as described earlier. During the sequential Bayesian update step, the model will marginalize over all student prototypes (rows of the matrix). The advantage of this approach is that we do not face the combinatorial explosion problem as we allow the model to learn the appropriate student prototypes to use. The disadvantage is that it assumes that new students can be categorized into roughly the same prototypes learned during training which, for large student cohorts, is not an unreasonable assumption.
3.3. Skill Discovery with the BKT RNN
Even though each problem in the datasets considered in this work is assigned to a knowledge component by experts, the true problem-KC assignment matrix is likely to be different from the expert-provided one. Indeed, it has been shown that extending BKT with mechanisms to discover problem-KC assignments significantly boosts performance (Lindsey et al., 2014, Ritter et al., 2009, González-Brenes and Mostow, 2012) and brings it level with DKT on some datasets (Khajah et al., 2016). Here, we assume that each problem maps to only one underlying KC. Specifically, we aim to find an assignment matrix of \(L\) problems to \(K\) underlying KCs, \(\mathbf {A} \in \{0,1\}^{L \times K}\), such as that each row of the matrix is all zeros except for one entry which has a value of 1. Prior approaches to estimating this matrix rely on ad-hoc two-step methods such as K-means clustering (Ritter et al., 2009), assume that the KC assignment changes on each trial (González-Brenes and Mostow, 2012), or use mathematically and computationally demanding extensions to the Chinese Restaurant Process (CRP) (Lindsey et al., 2014). In this section, we demonstrate a mechanism to estimate this discrete assignment matrix within an NN framework, which is a feat that, to our knowledge, has not been accomplished before.
The main challenge is that entries of the assignment matrix are binary while neural networks typically only work with continuous activations. To get around this, the assignment of each problem \(i\) is sampled from a categorical distribution \(\boldsymbol {\alpha }_i\). A categorical distribution is a discrete probability distribution over \(K\) values, with each value being assigned a probability mass \(\in (0,1)\) such that the sum of all probabilities equals one. Since the probability masses are continuous values, they have well-defined gradients and can be handled by existing NN optimization algorithms. The remaining problem is then to backpropagate through the randomly sampled KC assignment. Fortunately, the Gumbel-Softmax re-parameterization trick (Jang et al., 2017) enables this by transforming i.i.d. random samples from a \(g^{j} \sim Gumbel(0,1)\) distribution into samples from a categorical distribution with class probabilities \(\alpha _{i}^{j}\) as follows: \begin {align} a_{i}^{j}=\frac {exp\left (\left (log(\alpha _{i}^{j})+g^{j}\right )/\tau \right )}{\sum _{l=1}^{K}exp\left (\left (log(\alpha _{i}^{l})+g^{l}\right )/\tau \right )}\label {eq:gumbel} \end {align}
where \(a_{i}^{j} \in (0,1)\) is the soft binary variable indicating whether the \(i\)th problem belongs to the \(j\)th KC, and \(\tau \) is a temperature parameter that smoothly anneals the assignment between hard samples (as \(\tau \rightarrow 0\)) and uniform samples (for large values of \(\tau \)). For all experiments in this paper, \(\tau \) is set to a constant value throughout training. This trick works because it is straightforward to compute the derivative of the randomly sampled assignments in Equation \eqref{eq:gumbel} with respect to the class probabilities \(\boldsymbol {\alpha }_i\).
By sampling the assignment matrix, the optimization objective of the model changes from maximizing the probability of the observations under model parameters, to maximizing the expected probability of the observations under the problem membership probabilities: \begin {align} \mathbb {E}_{p(\mathbf {A})}\left (p(\mathcal {D} \mid \mathbf {A})\right ) & =\int p(\mathcal {D} \mid \mathbf {A})p(\mathbf {A})\\ & \approx \frac {1}{S}\left [\sum _{i=1}^{S}p(\mathcal {D} \mid \mathbf {A}^{(i)})\right ] \end {align}
where \(S\) is the number of samples to draw from the categorical distributions over the assignments of problems \(p(\mathbf {A})\), \(\mathcal {D}\) is the training set, and \(\mathbf {A}^{(i)}\) is the \(i\)th sampled assignment matrix.
One difficulty with KC discovery is that the whole model must be differentiable with respect to the sampled assignment matrix. The BKT RNN cells we have presented thus far do not accommodate this because they assume that the sequences will be split by KC. This splitting operation is not differentiable and thus the BKT layer has to be modified as shown in Figure 7. The state of the BKT cell now represents the knowledge probability of all \(K\) KCs (\(\mathbf {H}_t \in \mathbb {R}^{K \times 2}\)). At time \(t\), a one-hot vector representing the previous KC \(\mathbf {\kappa }_{t-1}\) is used to retrieve the relevant row from the state matrix (state read operation). This row is combined with the guessing, slipping, learning, and forgetting probabilities of the previous KC to generate the updated state of the KC, as per the usual BKT update dynamics (Equation \eqref{eq:hmmupdate}). The updated state is then written back into \(\mathbf {H}_t\) (state write operation). Finally, from this updated matrix, the row corresponding to the current KC \(\mathbf {\kappa }_t\) is used in conjunction with the KC’s guessing and slipping parameters to produce the prediction for time \(t\).
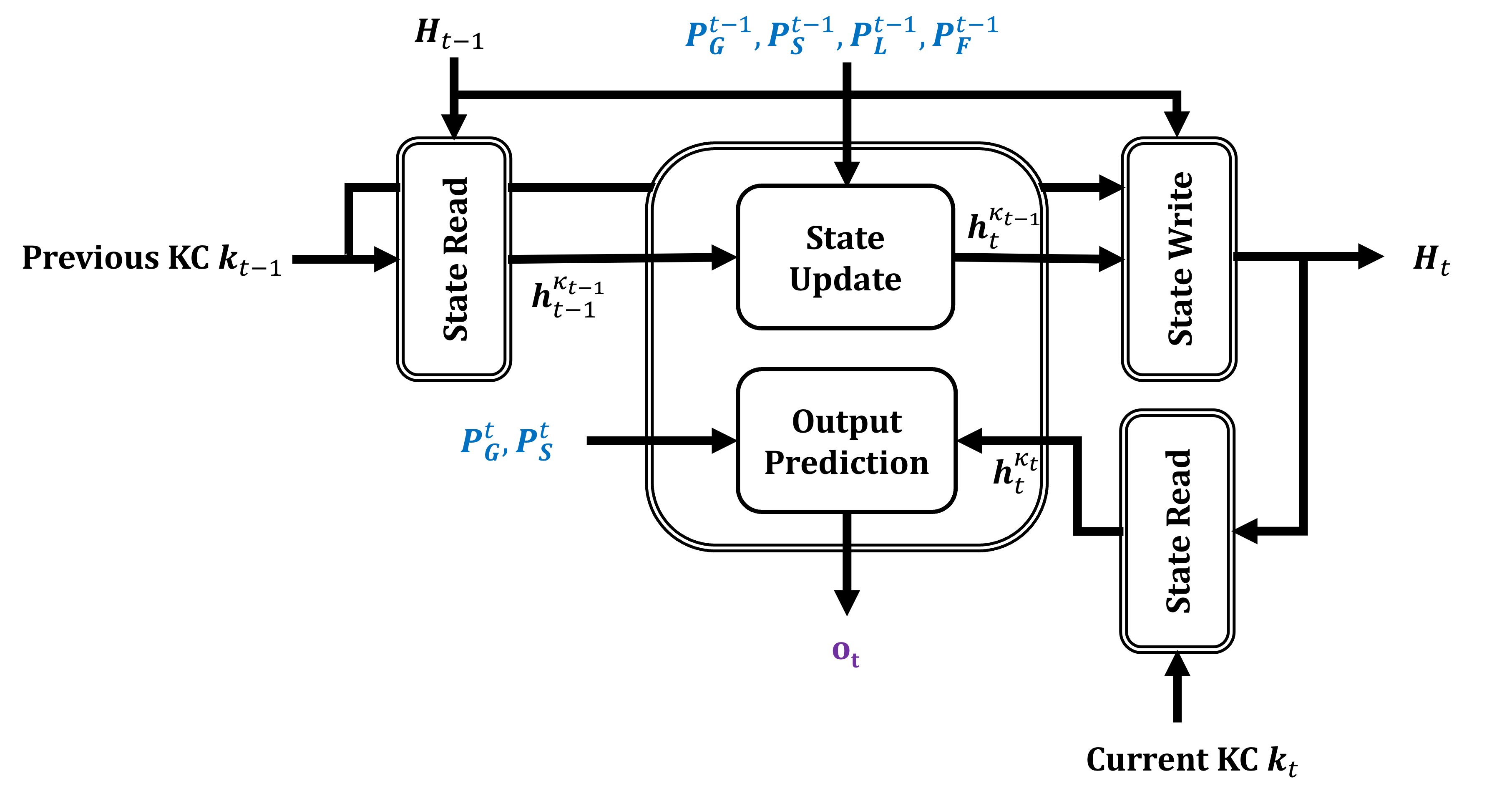
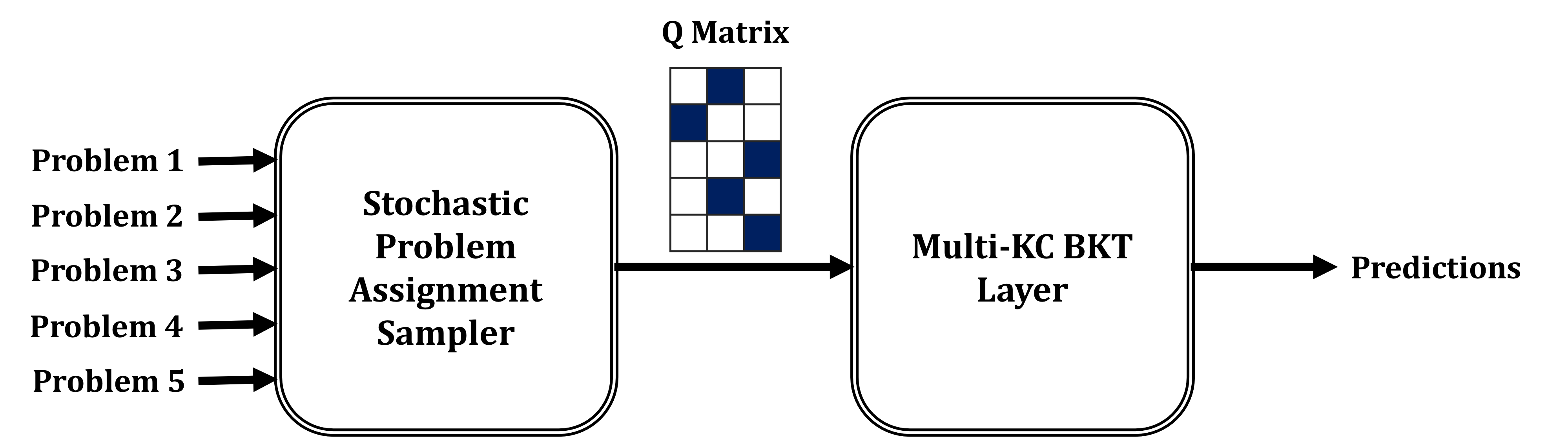
The above formulation is differentiable with respect to the parameters of the Gumbel-Softmax distribution. However, since the Gumbel-Softmax re-parameterization trick generates soft samples (where there is more than one non-zero entry in the sampled assignment vector), using the sampled assignment directly in the forward pass would not make sense from a probabilistic modeling perspective as BKT requires the assignment matrix to be strictly binary. To circumvent this, hard quantization on the sampled assignment matrix can be performed to replace the maximum entry in each row with one, and all other entries in the row with zeros. Of course, this is not differentiable so Jang et al. (2017) suggests using the Straight-Through (ST) gradient estimator where the gradient of the quantized matrix with respect to Gumbel-Softmax parameters is simply set to be the gradient of the soft matrix with respect to distribution parameters. In practice, we found that using the soft assignment matrix during training is more efficient, so all experiments in this paper do not use the ST estimator. Note, however, that the sampled assignment matrix is always quantized during evaluation to maintain the proper probabilistic dynamics of BKT. To summarize, Figure 8 illustrates high-level BKT with KC discovery architecture.
3.3.1. Using Problem Representations
One of the advantages of implementing BKT within an NN framework is the ability to utilize arbitrary encoding modules to parameterize the model. For example, a problem may have a feature vector \(\mathbf {r}_p\) capturing raw or salient attributes (e.g., problem text, image, audio, etc.). We can use these features to compute the guessing and slipping probabilities in the BKT+IRT model as follows: \begin {align} \text {logit}p_{G}(\mathbf {r}_{p}) & =g(\mathbf {r}_{p})+\theta _{u}\\ \text {logit}p_{S}(\mathbf {r}_{p}) & =f(\mathbf {r}_{p})-\theta _{u} \end {align}
where \(g\) and \(f\) are arbitrary differentiable functions. A more interesting approach, as pointed out by our reviewers, is to use problem features to discover KCs that satisfy BKT’s assumptions of KC independence and within-KC problem homogeneity. This can be done via a learnable membership function \(\mathbf {m}(\mathbf {r}_p)\) that transforms a problem feature vector of size \(F\) into a membership probability vector of size \(K\) (corresponding to \(K\) KCs). So, the skill discovery model can now use these problem representations to guide the search for the right problem-KC assignment matrix.
3.3.2. Auxiliary KC Discovery Loss
Prior information about the structure of the KCs can be used to guide the BKT KC discovery model via extra terms in the training objective. For example, we consider an auxiliary loss that rewards the model for finding problem-KC assignments that result in a “blocked” KC structure, where students practice all problems in one KC before moving on to the next. To compute this loss, we need the probability that a consecutive pair of trials will have the same KC annotation: \begin {equation} P(\kappa _{t}=\kappa _{t+1})=\sum _{j=1}^{K}a_{p_t}^ja_{p_{t+1}}^j \end {equation} where \(p_t\) is the problem encountered at time \(t\), and \(a_p^j\) is the probability that \(p\) belongs to KC \(j\). This probability is computed for all sequences and for all consecutive pairs of trials, resulting in the auxiliary loss: \begin {equation} \text {auxloss}(\mathcal {D})=\sum _{s=1}^{S}\sum _{t=1}^{N_{s}-1}P(\kappa _{t}=\kappa _{t+1}) \end {equation} where \(S\) is the number of students, and \(N_s\) is the number of trials practiced by student \(s\). Finally, the training objective of the KC discovery model becomes: \begin {equation} \mathcal {L}(\mathcal {D})=\mathbb {E}_{p(\mathbf {A})}\left (p(\mathcal {D}\mid \mathbf {A})\right )+\lambda \text {auxloss}(\mathcal {D}) \end {equation} where \(\lambda \) is a hyperparameter that controls the strength of the auxiliary loss.
3.4. Deep Knowledge Tracing (DKT)
DKT is a recurrent neural network model adapted for student performance modeling. As stated earlier, RNNs are trained by unrolling the recurrence relationship so that recurrent connections become simple feed-forward ones, like in ordinary neural networks. It turns out, however, that using generic neural networks for \(f\) in Equation \eqref{eq:rnn˙statespace} leads to poor performance due to difficulty in capturing long-term relationships in a sequence. Long-Short-Term-Memory (LSTM) units (Hochreiter and Schmidhuber, 1997) address this issue by propagating the cell state almost unchanged through the unit. DKT is simply an LSTM RNN with a \(K\) dimensional output corresponding to the probability of answering each KC correctly. The input to the LSTM unit is a one-hot vector of length \(2K\) that indicates what the KC at the previous trial was and whether the student answered it correctly or not. Unlike BKT, DKT works with entire student sequences and does not split them by KC. This gives the model the ability to leverage performance on different KCs to estimate the student’s ability (Montero et al., 2018). The main disadvantage is a lack of interpretability, i.e., model parameters do not have a clear interpretation. Even though this work is not intended to showcase models that outperform black box models, we include DKT to provide a familiar baseline in our comparisons.
3.5. Real-World Datasets
To evaluate the BKT RNN and its extensions, eight pre-processed real-world datasets published by
Gervet et al. (2020) were used so that direct comparisons to their models can be made.
Two datasets are based on the Algebra I 2005-2006 (algebra05) (Stamper et al.,
2010a) and Bridge to Algebra 2006-2007 (bridge_algebra06) (Stamper et al.,
2010b) datasets. Four datasets are created from the ASSISTments intelligent tutoring system in
2009-2010 (assistments09), 2012-2013 (assistments12), 2015 (assistments15), and
2017 (assistments17) (Feng et al., 2009). One dataset (spanish) is based on the
Spanish vocabulary learning system for middle school students (Lindsey et al., 2014),
and one dataset (statics) is from the civil engineering statics course dataset in PSLC (Koedinger
et al., 2010). Table 2 reports the main statistics of all datasets in terms of
the number of students, skills, and problems. Since all models are evaluated via five-fold
cross-validation, the average number of novel test problems (problems that have not been
seen in the training set) and the average number of test trials involving novel problems
are reported over the five splits. The % Blocking column is the median probability that
two consecutive trials will share the same KC. It is computed over all sequences in the
dataset.
To evaluate skill discovery with problem representations, we used the 2007 handwriting dataset
(Ritter et al., 2007, Anthony and Ritter, 2008) (the equations dataset). The dataset
was collected from a study that compared students using a standard cognitive tutor interface to
practice equation-solving exercises with those using a modified interface that recognizes
handwriting. In the control condition, students solve a question in multiple steps and are
provided with step-level feedback (we consider steps to be problems in this dataset). Only
trials belonging to the control condition are used because other conditions display worked
examples when students solve a problem. For the expert-provided skills, we use the default KC
model, with multi-KC assignments collapsed into one joint assignment. Performance on
each step is measured by the correctness of the student’s first attempt on the step. The step
name column in the dataset contains the equation that needs to be transformed to make
progress toward the solution. Equations in this column are cleaned by replacing all \(y\)s with \(x\)s
and all numeric values with uppercase letters. The equations are then embedded using the
all-mpnet-base-v2 pre-trained model from the sentence-transformers Python
module (Reimers and Gurevych, 2019), generating a 768-dimensional feature vector for each
problem.
| Dataset | Students | KCs | Problems | % Novel Test Problems | % Novel Test Trials | Median Seq Length | % Blocking |
|---|---|---|---|---|---|---|---|
| algebra05 | 567 | 271 | 173,113 | 68.57 | 25.86 | 580 | 17.1 |
| assistments09 | 3,114 | 149 | 17,708 | 3.36 | 0.98 | 32 | 77.8 |
| assistments12 | 22,589 | 265 | 52,850 | 4.28 | 0.41 | 59 | 71.1 |
| assistments15 | 14,228 | 100 | 100 | 0.00 | 0.00 | 31 | 78.6 |
| assistments17 | 1,708 | 411 | 3,162 | 4.34 | 0.18 | 442 | 73.4 |
| bridge_algebra06 | 1,130 | 550 | 129,263 | 10.66 | 2.58 | 1,376 | 31.5 |
| spanish | 182 | 221 | 409 | 0.00 | 0.00 | 2,857 | 3.4 |
| statics | 282 | 98 | 1,223 | 0.00 | 0.00 | 637 | 58.5 |
| equations | 22 | 114 | 1,193 | 28.00 | 14.00 | 341 | 16.6 |
4. Results and Discussion
In all experiments below, the models were trained and evaluated via student stratified five-fold cross-validation (so only new students are encountered during test time). The training portion of each fold was further split into 80% for optimization and 20% for early stopping (validation). With early-stopping, model training stops if the Area Under the Receiver Operating Characteristic Curve (AUC-ROC) (Bradley, 1997) does not improve on the validation set by at least 1% over the previous best for \(E\) epochs. In the case of the skill discovery models, this percentage was set to 0% so that model training does not end prematurely. AUC-ROC is the probability that a model ranks a positive instance higher than a negative one and ranges from 0.5 (random) to 1.0 (perfect). Following the practice in (Khajah et al., 2016), AUC-ROC is computed over the entire test set, not per KC. All models are trained to minimize the negative log-likelihood of the data (binary cross-entropy), via the NAdam (Dozat, 2016) optimizer.
4.1. Recovering BKT Parameters
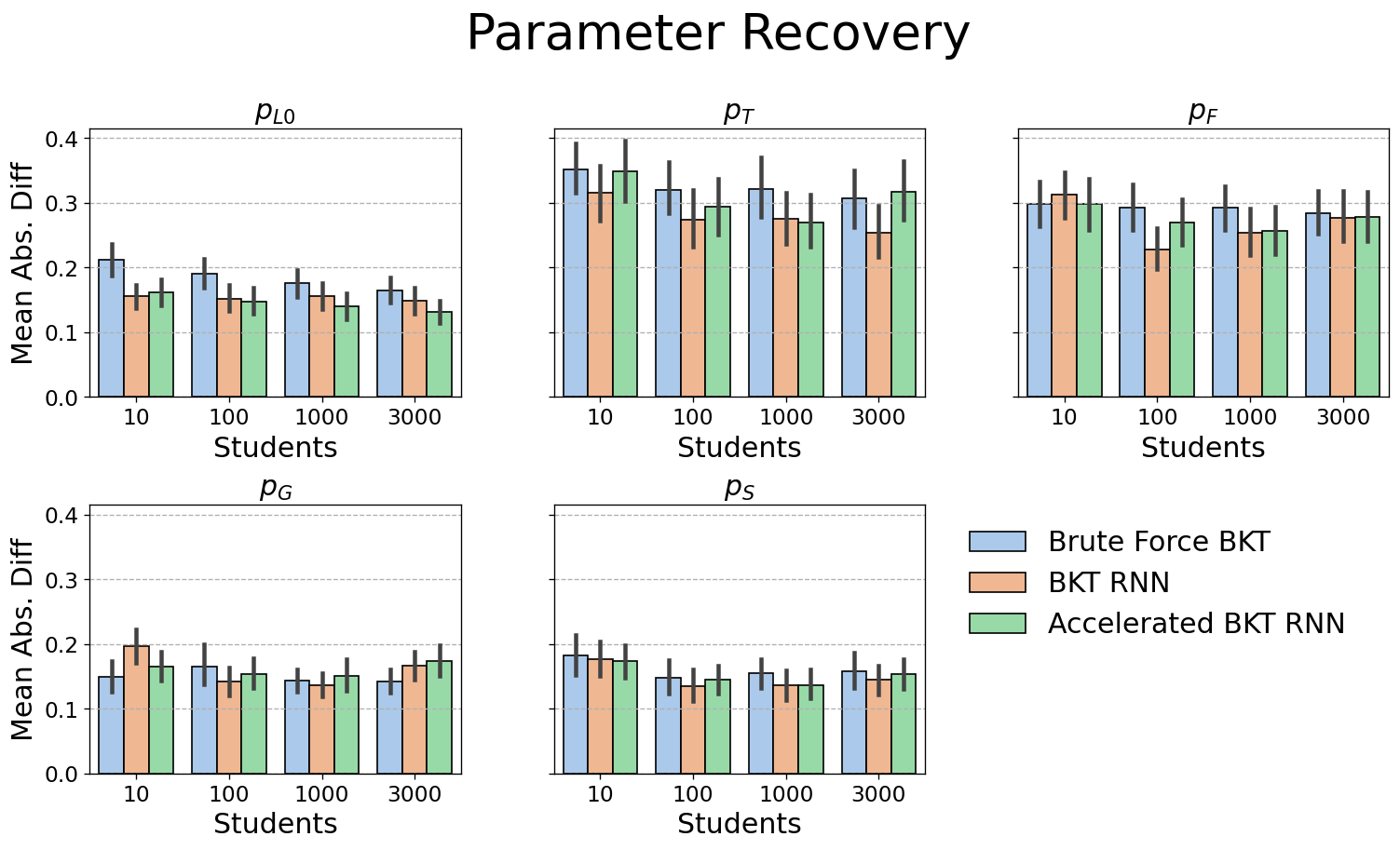
As we are proposing a new BKT implementation, it is critical to verify that it behaves identically to a standard BKT implementation; the learned BKT parameter estimates of BKT RNNs should be similar to those of a reference implementation. To test this, several BKT datasets were generated with varying numbers of students \([10, 100, 1000, 3000]\). Each dataset has 25 KCs with randomly initialized BKT parameters, and every student practices every KC 10 times. The reference implementation is a brute-force algorithm that performs grid-search over the 5-dimensional parameter space of BKT for each KC (the grid consists of 5 equally spaced points in the interval \([0,1]\) for each parameter, resulting in a total of \(5^5 = 3,125\) evaluations per KC). The reference and BKT RNN implementations were compared on how well they recapture the parameters that were used to generate the synthetic datasets. The accelerated BKT implementation used a stride \(C = 5\) (so it processed five trials at a time). Note that none of the implementations force state \(s_t = 0\) to correspond to not knowing and \(s_t = 1\) to knowing the KC. In other words, it is possible that after training, the state \(s_t = 0\) would correspond to knowing the KC and \(s_t = 1\) to not knowing the KC, thereby forcing the rest of the learned parameters to be reinterpreted. To break this symmetry, we assume the knowing state is the one whose initial knowledge estimate \(p_{I}\) is closest to the actual initial knowledge probability. Obviously, this is not possible with real datasets, but it suffices for the purposes of checking learning on a synthetic dataset.
Figure 9 compares the reference (blue bars), standard BKT RNN (orange bars), and accelerated BKT RNN implementations (green bars) in terms of how close their parameter estimates are to the generating parameters (mean absolute difference between estimated and actual values). All implementations recover the parameters directly associated with observations (\(p_G\), \(p_S\), \(p_{I}\)) better than the parameters governing the hidden state transitions (\(p_T\) and \(p_F\)). Both BKT RNN implementations are slightly better than the brute force model, most likely because the latter performs a search over a fixed grid, so it might miss good solutions, while the RNN implementations have no such limitation.
4.2. Scaling to Large Datasets
The training and prediction execution speed of BKT RNN and its accelerated variant was compared to the reference brute-force implementation and hmm-scalable (Yudelson, 2022), a C++ program designed specifically to fit HMMs at scale. hmm-scalable was configured to use gradient descent optimization and to allow forgetting in the BKT model. All other settings were left at their default values. BKT RNNs used training and testing batch sizes of 500 and 1000 sequences, respectively and training stopped if the validation AUC-ROC did not improve by at least 1% over the previous best for 10 epochs. In addition to comparing the execution speed of tested models, AUC-ROC is also reported to ensure that faster models do not compromise predictive accuracy.
The experiments were conducted on synthetic datasets generated as in the previous section, but with different numbers of students and trials per KC (10, 100, 1000, and 3000 students and 10, 50, 100, and 500 trials per KC) to evaluate whether sequence length has any impact on relative model performance. All experiments were conducted on a Ubuntu Linux Server 22.04 workstation with AMD Threadripper 3970X, 256GB RAM, and GeForce RTX 3090 TI. Although the processor has 32 cores, cross-validation was performed strictly serially: one split after another.
Figure 10 plots the execution times (training plus prediction) of the four models (top row) and their test set AUC-ROC (bottom row). Columns correspond to increasing sequence lengths (left to right). Across all sequence lengths, the brute force model is the slowest of the four models, and the hmm-scalable model is the fastest. The accelerated variant of BKT RNN (green) is consistently faster than the standard BKT RNN (orange). hmm-scalable’s advantage over accelerated BKT RNN shrinks as the size of the datasets increases, and it gets as small as 10-20% on a dataset of 3,000 students and 100-500 trials per KC. Note that the BKT RNN models were not fully optimized for performance and the execution speed could be improved with more suitable choices of early stopping patience, learning rates, and mini-batch sizes. Of course, the speed of brute force BKT can be improved by using more CPU cores (i.e., by having each core evaluate a subset of the search space). However, that model still suffers from a serious lack of flexibility.
The AUC-ROC results show that all models achieve similar performance. The brute force implementation is slightly ahead of both BKT RNN variants because it can avoid local minima by virtue of exhaustive search. BKT RNNs are both consistently better than hmm-scalable.
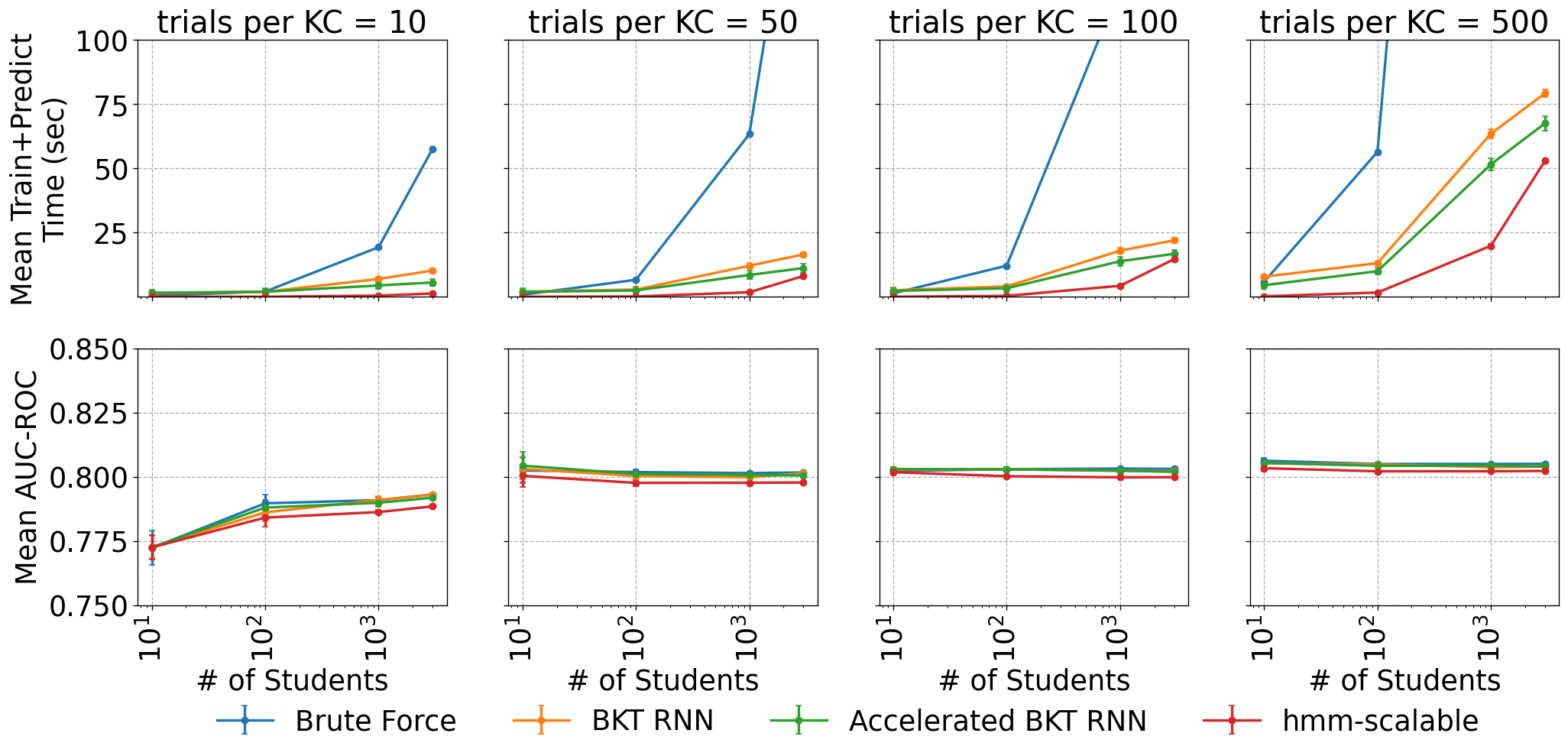
Table 3 lists the reduction in execution time of the accelerated BKT RNN relative to the standard BKT RNN. The first model can be as much as 47% faster than the second, depending on the size of the dataset. For short sequences, as the number of students increases, the accelerated model’s advantage increases, most likely due to it being able to fit and execute large batches on the GPU. For long sequences, the accelerated model’s advantage shrinks as the number of students increases, because it is a more memory-intensive model (due to the enumeration of all possible state space trajectories) so the execution time could be dominated by the cost of repeated memory allocations.
| Students | ||||
|---|---|---|---|---|
| Trials per KC | 10 | 100 | 1,000 | 3,000 |
| 10 | -34.7 | -31.4 | -41.2 | -47.4 |
| 50 | -34.6 | -30.7 | -31.1 | -33.3 |
| 100 | -27.8 | -28.8 | -24.1 | -24.3 |
| 500 | -45.7 | -25.0 | -18.8 | -14.7 |
As stated before and as we shall see in the following sections, the true advantage of BKT RNNs lies in their flexibility: the ability to extend the model without having to perform complicated mathematics and implement custom optimization algorithms. Specifically, all that is required to extend the model is a clear definition of the forward computation, which is usually easy to derive (as with all neural networks); the complicated backward pass is performed by PyTorch. Furthermore, BKT RNNs have substantially smaller, simpler, and easier-to-modify codebase (please see our our Github repository).
4.3. Skill Discovery
4.3.1. Synthetic Datasets
A comprehensive set of synthetic experiments where the true problem-KC assignments are known
were conducted to test the skill discovery model’s ability to recover those assignments. Three synthetic
datasets consisting of 5, 25, and 50 skills were generated, with 10 problems per KC and 100 students.
For each skill, student answers are generated according to a standard BKT model with randomly
chosen parameter values (\(p_G\) and \(p_S\) ranged from \(0.1\) to \(0.4\), \(p_L\) and \(p_F\) ranged from \(0.01\) to \(0.2\), and \(p_I\) ranged from \(0.1\)
to \(0.9\)). The problem-skill assignment matrix is created as follows: for each dataset, a set of \(K\)
50-dimensional centroids were generated (\(K\) is the number of skills). A blob of 10 points
was then generated around each centroid, corresponding to the 10 problems in the skill.
The width or standard deviation of generated points was chosen such that a simple nearest
neighbor classifier would have 85% accuracy in predicting a problem’s blob. Blob generation
was performed using the make_blobs() function in Python’s sklearn library. Two
versions of each dataset were generated: blocked and interleaved. In the blocked version, all
problems within a KC are practiced before moving on to the next (e.g., KC 1, 1, 2, 2, 3,
3), while in the interleaved version KCs are practiced in an alternating fashion (e.g., KC
1, 2, 3, 1, 2, 3). Problems are randomly shuffled within a KC for each student, so no two
students will have the same problem sequence, but KCs are always practiced in the same
order.
Seven BKT models were evaluated in terms of cross-validation AUC-ROC and adjusted Rand index (ARI) (Hubert and Arabie, 1985), which measures the agreement between discovered and actual problem-KC assignments. The index calculates the proportion of all pairs of problems where the true and predicted problem-skill assignments agree. Agreement between the assignments of two problems occurs when either (a) both problems belong to the same skill in the discovered and actual assignments or (b) both problems belong to different skills in the discovered and actual assignments. This formulation handles permutations in the assignments. For example, suppose that problem 1 belongs to skill A, and problems 2 and 3 belong to skill B, and that the model finds that problem 1 belongs to \(B'\) and problems 2 and 3 belong to \(A'\) (where \(A'\) and \(B'\) are the labels assigned by the skill discovery model). In this case, the two assignments are equal because all pairs of problems are in agreement: \((1, 2)\) belong to different skills in the true and discovered assignments, \((2, 3)\) belong to the same skill in both assignments and so on. The adjusted Rand index accounts for two assignments agreeing purely by chance. The index ranges from -0.5 to 1, with 1 and 0 representing perfect and no correspondence, respectively (negative values indicate worse correspondence than chance). The unadjusted Rand index (RI) does not correct for chance agreement. It also does not always follow its adjusted counterpart, so two models can have the same RI value but one can have significantly higher ARI than the other. This is because the chance correction in ARI assumes a random permutation with the same number and size of the discovered KCs. For this reason, we report both RI and ARI, but we focus on ARI when evaluating skill discovery performance.
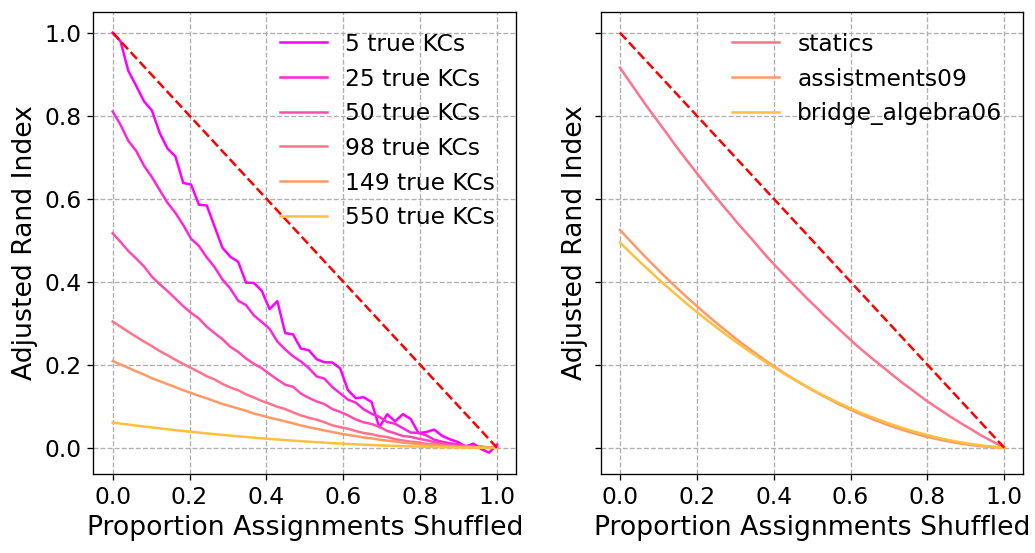
One way to interpret the Rand index is to determine how much the ground truth assignments should
be shuffled to achieve a given index value. The left panel of Figure 11 simulates multiple
scenarios with varying numbers of KCs in the ground truth assignments (5, 25, 50, 98, 149, and
550; the last three scenarios correspond to the number of KCs in three real-world datasets)
and 10 problems per KC. In each scenario, we assume we have a hypothetical predicted
assignment containing up to 20 KCs. This predicted assignment is generated by shuffling a
random proportion of the true assignments (the proportion is the x-axis in the Figure). If the
number of true KCs is greater than 20, problems belonging to the extra KCs are equally
distributed amongst the 20 predicted KCs. This is what we call a random permutation model. The
adjusted Rand index is always less than the shuffling proportion (except for the trivial cases at
0 and 1). When the number of KCs in the true assignment is greater than the maximum
available KCs in the predicted assignment, it cannot possibly achieve a perfect index, hence the
corresponding curves start at a value less than 1.0. To see how non-uniform assignments
affect the analyses, the right panel of Figure 11 simulates three scenarios with the same
distribution of assignments in the statics (98 KCs), assistments09 (149 KCs), and
bridge_algebra06 (550 KCs) datasets. The latter two datasets have very similar curves,
despite the large difference in the number of KCs, and both curves are substantially different
from their counterparts in the left panel with the same number of KCs. The takeaway from
this Figure is that the adjusted Rand index is sensitive to the distribution of ground truth
assignments, and it can give the impression of worse performance than reality. For example, for
25 true KCs, an adjusted rand index of 0.6 would correspond to shuffling roughly 17% of
the true assignments, not 40%. For this reason, we report the adjusted Rand index and the
corresponding % of the assignments shuffled by a random permutation model in the skill discovery
experiments.
We also evaluate the percentage of true KCs that are recovered by the skill discovery models. A KC is considered “recovered” if it matches any of the discovered KCs. A discovered KC \(D\) matches a true KC \(T\) if \(D\) contains all of \(T\)’s problems and none of the problems that do not belong to \(T\). This definition corresponds to the familiar recall and precision metrics from binary classification. Specifically, we consider \(D\) to match \(T\) if its recall and precision is \(\ge 0.75\) (because no skill discovery model will perfectly recover skills). Based on this, we compute a weighted average of the recovered KCs, with each true KC weighted by the number of problems it contains: \begin {equation} V=\frac {1}{P}\sum _{i=1}^{K}n_{i}r_{i}\quad r_{i}\in \{0,1\} \end {equation} where \(P\) and \(K\) are the number of problems and true KCs, respectively, \(n_i\) is the number of problems in the \(i\)th KC, and \(r_i\) is whether the \(i\)th KC was recovered or not. A skill discovery model whose maximum number of KCs \(M\) is less than the true number of KCs in the dataset cannot possibly recover all KCs. The best it can do is to recover the top \(M-1\) largest KCs. The upper limit on \(V\) in this case is \(\frac {1}{P}\sum _{i=1}^{M-1}n_{i}\) (where the \(n_i\)s are sorted in descending order).
In the following experiments, the No SD model assumes each problem is its own KC, Single KC assumes there is one KC, SD is BKT with KC discovery, SD+AuxLoss is the same model but with auxiliary blocked KC loss (the auxiliary loss coefficient \(\lambda \) was set to 1), SD+Rep uses the problem input features to infer the Q-matrix, and SD+AuxLoss+Rep uses both auxiliary loss and problem input features. The Clustering model uses K-means clustering to cluster the problem representations into 20 clusters and then runs BKT with the resulting assignments, similar to the approach by Li et al. (2013). Finally, a BKT model that has access to the true problem-KC assignments is used as a reference.
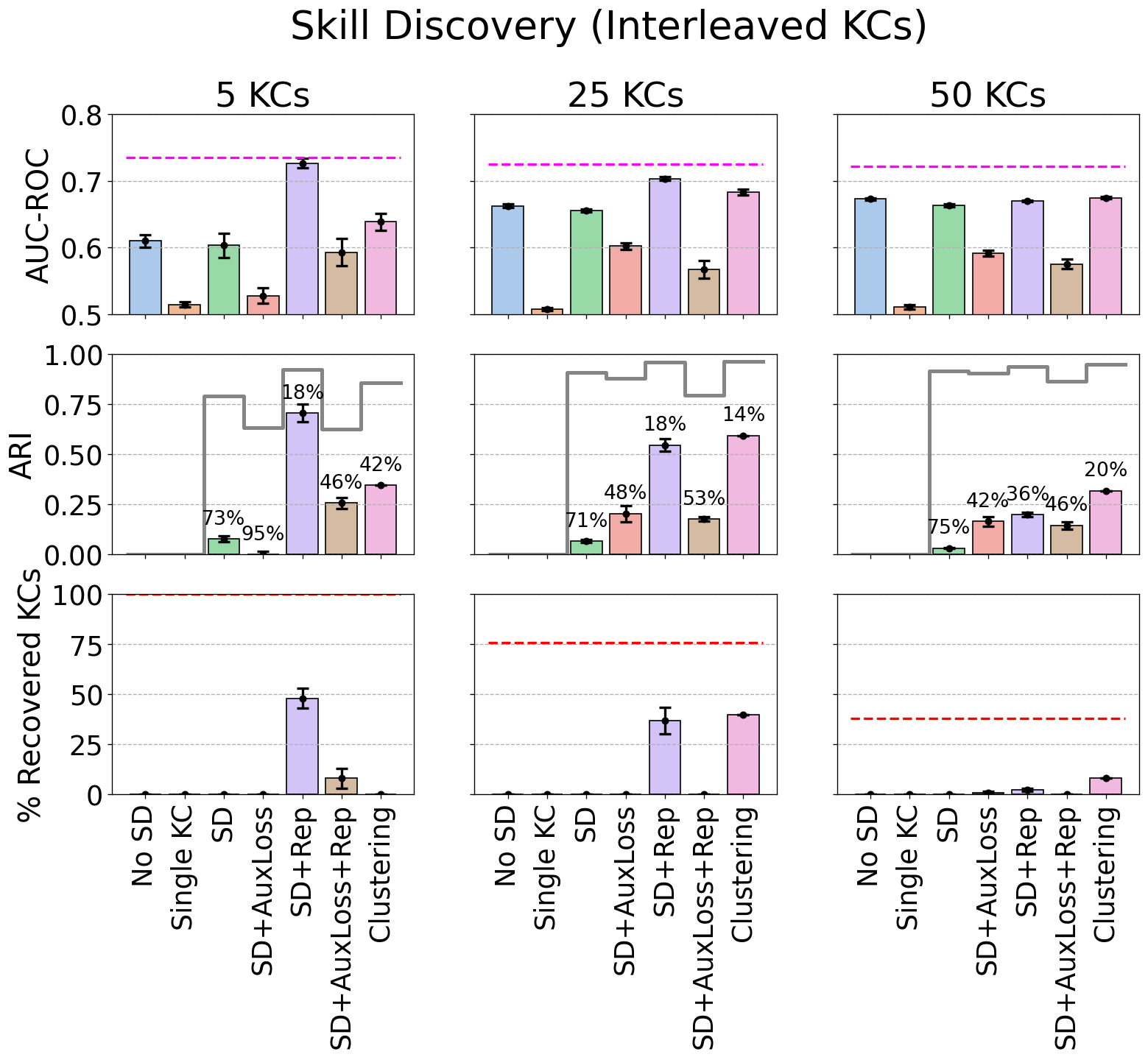
Figure 12 reports the 5-fold cross-validation test set AUC-ROC performance (top row), adjusted Rand index (middle row), and percentage of recovered KCs (bottom row) on the three synthetic datasets (with KCs ordered in blocks). As stated earlier, for each adjusted Rand index value, we report the corresponding percentage of assignments shuffled by a random permutation model to aid the interpretability of the results. For reference, the unadjusted Rand index value is also reported (gray lines), as well as the upper limit on the number of KCs recovered (red dashed lines). The SD model fails to improve over the No SD model and achieves Rand index values which correspond to 60-70% shuffling of the true assignments. SD+AuxLoss achieves AUC-ROC close to the true model for KCs = 25 and 50 and achieves reasonable Rand index values that correspond to 18% to 26% permutation of the true assignments, respectively. SD+Rep is similar, except that the assignments it found when KCs = 50 are not as good as those found by SD+AuxLoss. This indicates that it is finding a problem-KC assignment and KC parameters that are nearly as good as the generating model. Adding the auxiliary loss to the model (SD+AuxLoss+Rep) enables the model to almost find the true assignments when KCs=5, and to find assignments that correspond to only 12% shuffling when KCs = 25. Finally, the clustering model is only able to match SD+Rep in predictive accuracy when the number of KCs = 50. Its assignments are much worse in quality than SD+Rep when KCs = 5, but they improve as the number of true KCs increases. The clustering model’s reduced predictive performance is likely due to its rigidity: it assigns problems into exactly 20 KCs before training BKT with those assignments. Our models, on the other hand, use the data to infer the number of true KCs (up to the limit of 20 KCs).
In terms of the percentage of KCs recovered, SD+AuxLoss+Rep recovers almost all KCs when the number of KCs = 5. The clustering model fails because, as stated earlier, it assigns problems to exactly 20 KCs before training BKT. As the number of KCs in the dataset increases, the recovery percentage drops and so does the upper limit. At 25 KCs, the clustering and SD+AuxLoss+Rep models recover about half of the possible KCs. At 50 KCs, SD+AuxLoss+Rep is the strongest and recovers about a third of the maximum possible KCs.
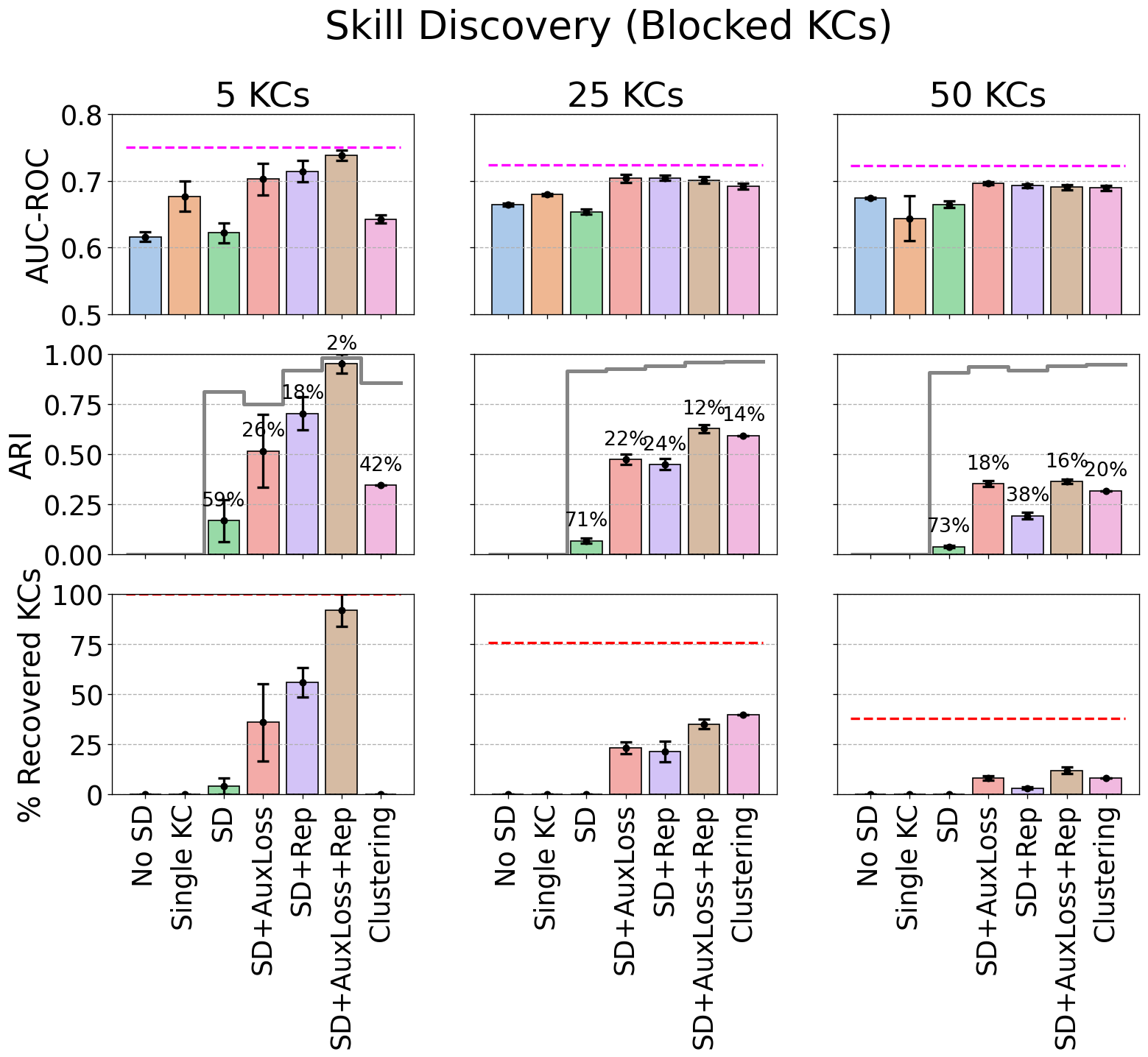
Figure 13 shows the results on synthetic datasets with interleaving KCs. The SD model performs similarly to the blocked case in terms of predictive accuracy and matches SD+Rep when KCs=50. SD+AuxLoss performs worse because it tries to impose an improper blocked structure over the interleaved KC sequences. SD+Rep performs best when KCs = 5 and 25, perhaps because it has enough capacity for the number of KCs in the dataset. It also discovers reasonably good assignments that correspond to 18% shuffling of the true assignments when KCs is less than 50, although it only recovers about half of the maximum possible KCs. SD+Rep+AuxLoss understandably does not perform as well due to the inclusion of the auxiliary loss term which does not match the underlying dataset. As the number of KCs increases, the No SD model matches the skill discovery models, because, under an interleaving structure with many KCs, the learning algorithm would have to capture very long dependencies (i.e., it would have to infer that a problem 50 trials back belongs to the same KC as the current problem). When the number of KCs is less than 50, SD+Rep outperforms the clustering model in predictive accuracy, and the latter finds significantly worse assignments when KCs = 5, again due to its rigidity. When KCs = 50, only the clustering model is able to recover even about a fifth of the maximum possible KCs.
Real-world datasets may not exhibit a strictly blocking or interleaving pattern. The % Blocking
column in Table 2 clearly demonstrates this, with the probability of consecutive trials sharing the same
skill reaching as high as 78% and as low as 3.4% on some datasets. Therefore, it is important to analyze
the skill discovery model’s performance on synthetic datasets that mimic the real-world ordering of the
skills. To do this, we created three shadow datasets based on the bridge_algebra06,
assistments09, and statics datasets, which cover a wide range of blocking percentages
(31.5%, 58.5%, and 77.8%, respectively). Shadow datasets are identical to their real-world counterparts
(they have the same skill and problem sequences) except that observations are generated
synthetically. For example, Koedinger et al. (2023) used a procedure to generate
simulated student data according to an individualized additive factors model (iAFM) whose
parameters were fitted on real datasets. Their objective was to detect variability in student
learning rates if it was present, so they scaled the fitted parameters to produce low and/or high
variability in initial knowledge and learning rates, respectively. Instead of pre-fitted iAFM, our
procedure uses BKT with randomly chosen probabilities as the generating model. To generate
problem representations, we used the same procedure as described earlier in the section. The
SD and clustering models used 50 KCs to handle the greater number of KCs in real-world
datasets.
Figure 14 shows a clear tension between achieving predictive performance (AUC-ROC) and recovering as many KCs as possible (ARI and the percentage of recovered KCs). If the objective is recovery, the clustering model performs very well on two of the datasets. But if the objective is high predictive accuracy, then SD+Rep is almost level with the true generating model. The reason for this tension is the limited capacity of the skill discovery and clustering models (50 KCs) compared to the true number of KCs in the datasets. SD+Rep utilizes its available capacity to find assignments that maximize accuracy, even if it means conflating several KCs, while the clustering model prioritizes recovery over anything else (by design). In other words, even if it perfectly recovered the top 49 KCs (by size) in each dataset, the clustering model has no way of dealing with the rest of the non-recovered KCs.
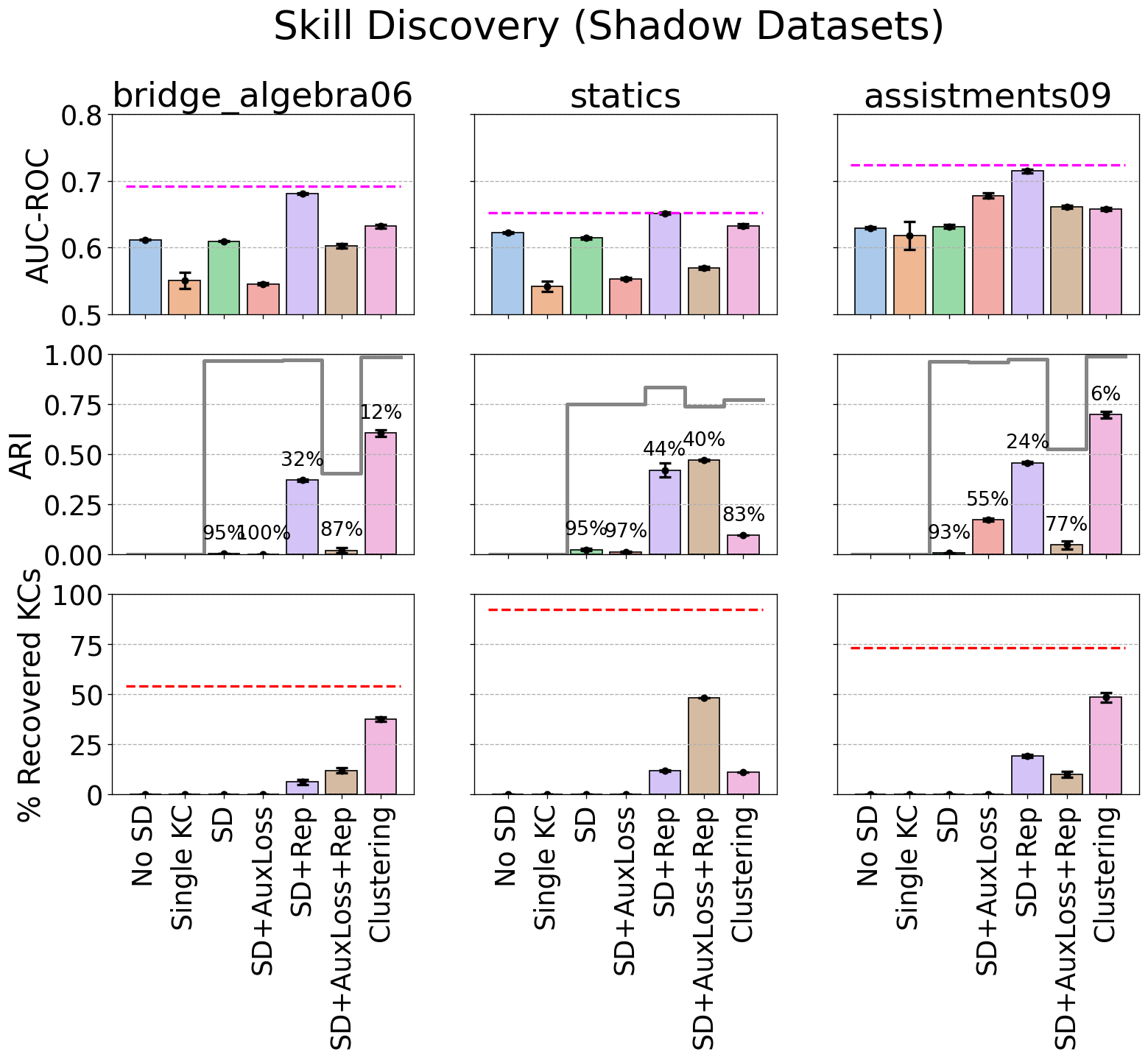
It is understandable that, as the number of true KCs increases, skill discovery becomes harder. KC discovery involves determining which problem subsets belong “together”, while simultaneously determining the BKT parameters of those subsets. As the number of true KCs increases, not only does it become more difficult to elucidate dependencies amongst problems, but KC parameters will be harder to distinguish, leading to identifiability issues. The model can be guided with the auxiliary loss term, as long as the loss matches the underlying KC sequencing structure in the dataset.
Overall, the skill discovery experiments demonstrate that when problem representations are available, predictive performance will be high, and the true problem-KC assignments can be recovered partially, although there is still room for improvement compared to the clustering model on realistically distributed datasets. The experiments highlight the importance of end-to-end learning of KC assignments and BKT parameters, as doing the two steps separately (as in the clustering model), often yields worse predictive performance.
4.3.2. Real-World Representation Learning
Figure 15 shows the AUC-ROC of the skill discovery models on the real-world equations
dataset which contains raw problem content. The skill discovery and clustering models used 50 latent
KCs (we also evaluated variants with 20 KCs, which had slightly worse performance) and the patience
parameter for early stopping was increased from 10 to 50 epochs as the model’s validation loss tends to
oscillate more on this dataset. The expert KCs model is BKT with expert-provided KC
annotations (extracted from the KC (Default) column in the dataset). Problem representations
bring the skill discovery model level with the expert-provided BKT model, despite using
fewer KCs (50 latent KCs versus 114 expert-provided KCs). The clustering model performs
slightly worse than skill discovery and expert BKT models. The skill discovery model found
a total of 15 KCs, so it is much more sparse than the clustering and expert models. We
should note at this point that the problem-cleaning step described in the datasets section is
critical to achieving this performance, without which the prediction accuracy is reduced
noticeably.
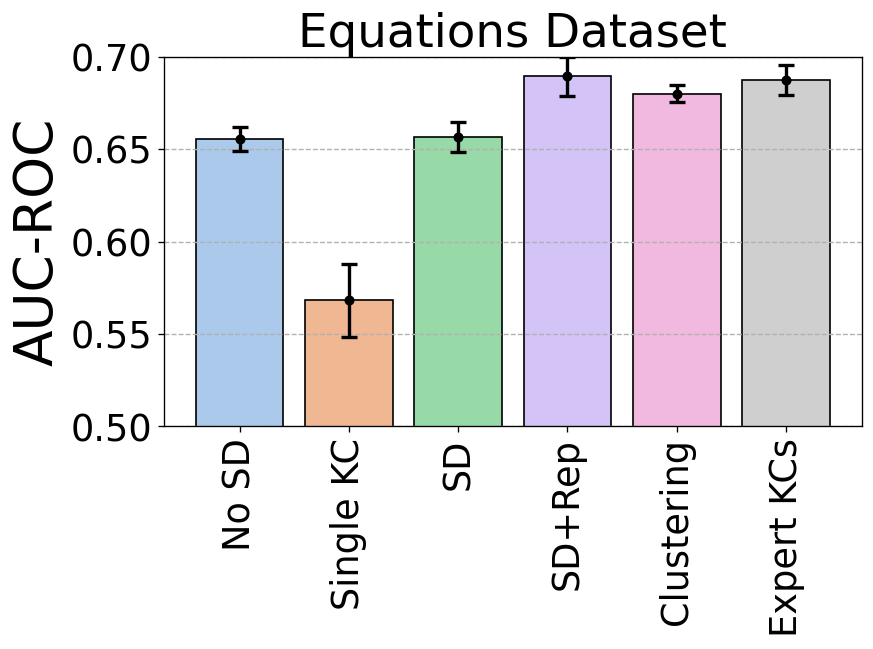
Table 4 illustrates the top 5 tokenized representations of the problems in the four most frequently used KCs by the SD+Rep model on one cross-validation split. Initially, we struggled to provide good labels for the discovered KCs but our reviewers have kindly provided examples to do so. Problems under KC1 require the student to move the terms involving the variable to one side of the equation if a mixture of constants and variables appears on one side. Under KC2 it is the opposite: the problems require the student to move all constant terms to one side of the equation if constants and variables appear on one or both sides. KC3 problems require the student to multiply both sides by a constant, if the equation has a term on each side, and the constant divides the variable on one side. KC4 problems require the student to cancel a constant on both sides, if the equation has one term on each side, and each term contains the constant.
One of our reviewers suggested examining whether students learn with repeated opportunities on the discovered KCs (i.e. \(p_L > 0\)) as a way of measuring the quality of the KCs’ interpretability. On the skills discovered in Table 4, \(p_L\) is 0.004, 0.004, 0.310, and 0.085 for KC1, KC2, KC3, and KC4, respectively. Those estimates are based on a single cross-validation split. Across all cross-validation splits, the average 25%, 50%, and 75% quartiles of \(p_L\) are 0.057, 0.160, and 0.495, respectively (i.e., on average, 50% of discovered KCs with at least one problem have \(p_L > 0.160\)). We can improve the interpretability of discovered KCs by requiring that \(p_L\) be greater than some threshold value, which can be done with a straightforward mathematical transformation in the model.
The results on the equations dataset show that problem representations can be used to drive end-to-end skill discovery without the need for expert annotations. Of course, more performance could be unlocked with a more suitable choice of embedding models, such as those that can directly embed tree-structured data (an equation or mathematical expression is a tree structure). In the next set of experiments, we evaluate how the basic SD model performs on other real-life datasets, where no representations are available and assumptions about the true KC sequence structure cannot be made.
| KC1 | KC2 | KC3 | KC4 |
|---|---|---|---|
| \(-A-Bx=Ax\) | \(A-A=A+Bx-A\) | \(\frac {-x}{-A}=\frac {A}{-B}\) | \(A=\frac {Ax}{A}\) |
| \(Ax=Ax-B-Ax\) | \(A-B=A+Bx-A\) | \(\frac {-x}{-A}=\frac {-A}{-B}\) | \(A=\frac {A}{x}\) |
| \(Ax=-Ax-B-Ax\) | \(x-A=-Ax+B\) | \(\frac {-Ax}{-A}=\frac {-A}{-B}\) | \(-A=\frac {Ax}{A}\) |
| \(Ax=A-Bx\) | \(A-B=A+-Bx-A\) | \(\frac {A}{-B}=\frac {-x}{-A}\) | \(\frac {A}{A}=\frac {Ax}{A}\) |
| \(-A-Bx=-Ax\) | \(x=A+B\) | \(\frac {-A}{-B}=\frac {-x}{-A}\) | \(A=Ax\) |
4.4. Evaluation on Real-World Datasets
Six variants of BKT were evaluated on eight real-world educational datasets. BKT is brute-force BKT, BKT+Abilities is accelerated BKT RNN equipped with inference of student abilities, BKT+Problems is accelerated BKT with problem-specific guess and slip probabilities, BKT+IRT combines student abilities and problem effects, BKT+IRT (Multidim) is BKT+IRT with student prototypes and multidimensional student abilities, and SD is BKT equipped with problem-KC assignment discovery (no auxiliary loss or problem representations).
BKT RNN models without skill discovery were trained with a learning rate of 0.5 and early-stopping patience of 10 epochs without a minimum improvement of 1% over the previous best. Depending on the dataset, the training batch size was changed to fit in the memory of the GPU (minimum and maximum batch sizes were 10 and 500 sequences, respectively). BKT+IRT used 13 equally spaced ability levels in the interval \([-3, 3]\) and the multidimensional variant used 20 student prototypes. For BKT+SD, the learning rate was set to 0.1, early-stopping for 10 epochs without improvement over the previous best, training batch size of 100 sequences, \(\tau = 1.5\), maximum of 20 underlying KCs, and 10 hard samples of the problem-KC assignment matrix for evaluation.
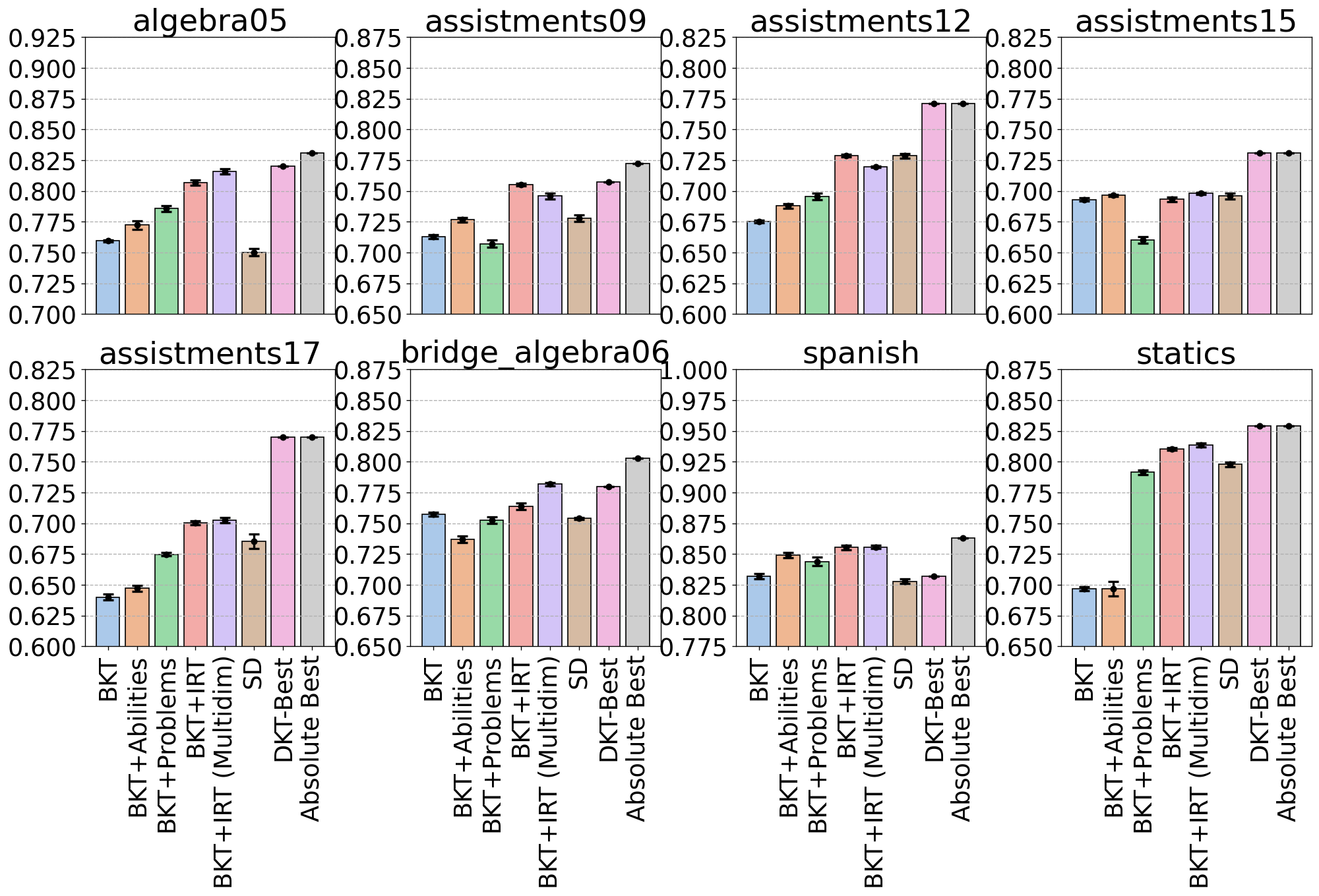
Figure 16 reports the test AUC-ROC of the six tested models on eight datasets. For reference, the
best-performing DKT model results from Gervet et al. (2020) are included (pink bars). Since they
evaluated a variant of DKT that is strictly limited to KC information and a variant that uses problem
and KC information, DKT-Best corresponds to the variant that achieves the higher AUC-ROC of the
two. Note, however, that they were not able to evaluate the second variant on datasets with a
large number of problems: algebra05, assistments15, and bridge_algebra06.
Also included is the absolute best model from Gervet’s paper, which we term Absolute
Best.
On the algebra05 dataset, incorporating problem effects (green) provides a greater boost in
performance over vanilla BKT than student abilities (orange). Combining abilities and problem effects
(red) provides a moderate increase over the problems-only model. Adding multiple student ability
dimensions (purple) provides another small increase over the uni-dimensional BKT+IRT model with
the model drawing almost level with DKT but lagging behind the absolute best model. SD lags behind
the other models, most likely because 26% of the test trials involve novel problems that have no
problem-KC assignment. The IRT-based models have better performance, even though they also use
problem-specific parameters, because their guessing and slipping probabilities are decomposed into the
sum of KC- and problem-specific parameters, with the latter being initialized to zero (see Methods
section). This allows the models to use KC parameters when a new problem is encountered during
evaluation.
On assistments09, combining student and problem effects leads to a clear improvement over
either set of effects alone (red bars vs orange and green bars). BKT+IRT also matches DKT but
lags behind the absolute best model. This supports the importance of modeling student
abilities on this dataset, which explains the SD model’s reduced performance as it does not
incorporate student effects. The multidimensional BKT+IRT model fares slightly worse than the
uni-dimensional variant, perhaps because the latter does not assume that it will encounter the same
kinds of students on testing as in training (because of the uniformly spaced ability values
grid).
On assistments12, BKT+IRT outperforms both BKT+Abilities and BKT+Problems. SD
matches it despite not using KC information and lacking student effects (it may be finding a KC
assignment that mitigates the lack of ability inference, such as one that uses few KCs). Again,
BKT+IRT (Multidim) fares slightly worse, potentially due to the assumption of student homogeneity
between training and testing. Results on assistments15 show a different picture: here,
BKT+Problems is substantially worse than BKT+Abilities because the dataset has 100 KCs and 100
problems, with one problem per KC. Thus, BKT+Problems on this dataset reduces to BKT, albeit with
additional unnecessary parameters which might have crippled training performance compared to
standard BKT. Indeed, the fact that BKT+IRT and its multidimensional variant only barely match the
BKT+Abilities model indicates that problem information does not really contribute anything to
predictive performance. SD outperforms BKT+Problems and matches BKT+Abilities, most likely due
to it finding a better assignment of problems to KCs. On the final ASSISTments dataset
(assistments17), BKT+IRT and its multidimensional counterpart are the best of BKT variants,
with the SD model fairing worse, which could be due to the lack of student effects in the
model.
On bridge_algebra06, multidimensional BKT+IRT matches DKT’s performance. None of the
other variants can improve over plain BKT. On spanish, DKT performs similarly to BKT, with
BKT+IRT and its multidimensional variants coming out on top. The SD model is not able to
improve over BKT, likely due to the declarative nature of the task in this dataset (foreign
language learning). Finally, on statics, all BKT extensions that use problem information
significantly outperform BKT and are close to DKT. The SD model again appears to be suffering
from the lack of student effects. All in all, the Absolute Best model’s greatest performance
advantage is on the assistments17 dataset, where it scores 0.07 AUC-ROC points higher
than BKT+IRT. On the remaining datasets, its advantage never exceeds 0.04 AUC-ROC
points.
We should note that the task of finding problem-KC assignments and fitting BKT parameters
simultaneously sometimes makes the SD model orders of magnitude slower than the other models,
depending on the size of the dataset. The model’s longest runtime is on the assistments12 dataset,
where it takes an average of 51 minutes per cross-validation fold, compared to BKT+IRT’s 66
seconds (46-fold difference). The smallest difference between the two models is on the
statics dataset, where SD and BKT+IRT take 15.1 and 4.4 minutes, respectively (3.45-fold
difference).
4.5. BKT+IRT Interpretability
To demonstrate the interpretability of our models, we looked at BKT+IRT’s strongest showing, the Bridge to Algebra 2006 dataset, where it matched DKT. Model parameters were constrained such that the not-slipping probability is always greater or equal to the guessing probability for skills, problems, and student prototypes. This is to force the model to produce cognitively plausible parameter estimates. The constrained model’s test performance did not change on the Bridge to Algebra dataset. The results below are based on the model being trained on one of the cross-validation splits in the dataset.
4.5.1. Visualizing Skill, Problem, and Student Effects
The blue panels in the top row of Figure 17 plot the KC probabilities when problem and student effects are set to zero. Points in the scatter plots correspond to individual skills. Guessing probabilities are symmetrically distributed with a peak at 0.5. As expected, slipping probabilities are skewed towards smaller values, with the most frequent value being near zero. The diagonal points correspond to skills where the probability of guessing is equal to not slipping; that is, whether the student knows the skill makes no difference (around 27% of the skills). This may seem odd but remember that the observation probabilities of BKT+IRT are functions of the sum of skill, problem, and student effects, not just skill effects alone. Learning and forgetting probabilities are skewed towards high and low values, respectively, but there is no clear relationship between them. Initial knowledge probabilities are skewed towards low values but they too have no clear relationship with learning probabilities.
For problems (orange panel in the top row of Figure 17), the picture is different. Most problems have a baseline guessing probability of 0.5, but a significant fraction has guessing probabilities greater than 0.70 (a baseline guessing probability of 0.5 means that the problem does not contribute to its KC’s guessing probability). The difficulty of all problems remains the same regardless of whether the student knows the skill or not (all problems are on the diagonal). This experimentally agrees with earlier approaches that used one parameter to characterize problem difficulty in models that merged BKT and IRT (Khajah et al., 2014). The reader might find it odd that the guessing and slipping probabilities for problems are exactly equal. This is because the model parameterizes a problem’s not-slipping probability in terms of the guessing probability and some non-negative boost. The boost is initialized to zero so if the model does not require it, it will stay at zero, making the guessing and slipping probabilities equal.
Since BKT+IRT parameterizes BKT probabilities using KC, problem, and student effects, it is important to see how they interact with each other. To illustrate this, we picked the most frequent student prototype (denoted as prototype T) and generated scatter plots of the five BKT probabilities (bottom row of Figure 17). Including student and skill effects shifts the guess probability downwards and skews the slipping probabilities toward zero. This is not unexpected as prototype T has small guessing and slipping offsets, as we shall see shortly. The concentration of slip probabilities near zero indicates that, for all problems, students are unlikely to slip once they have mastered the KC. Similarly, the learning and forgetting probabilities are also skewed towards lower values when including student and skill effects, because of prototype T’s small learning and forgetting offsets. The initial knowledge probabilities are unaffected because they are only a function of skill effects.
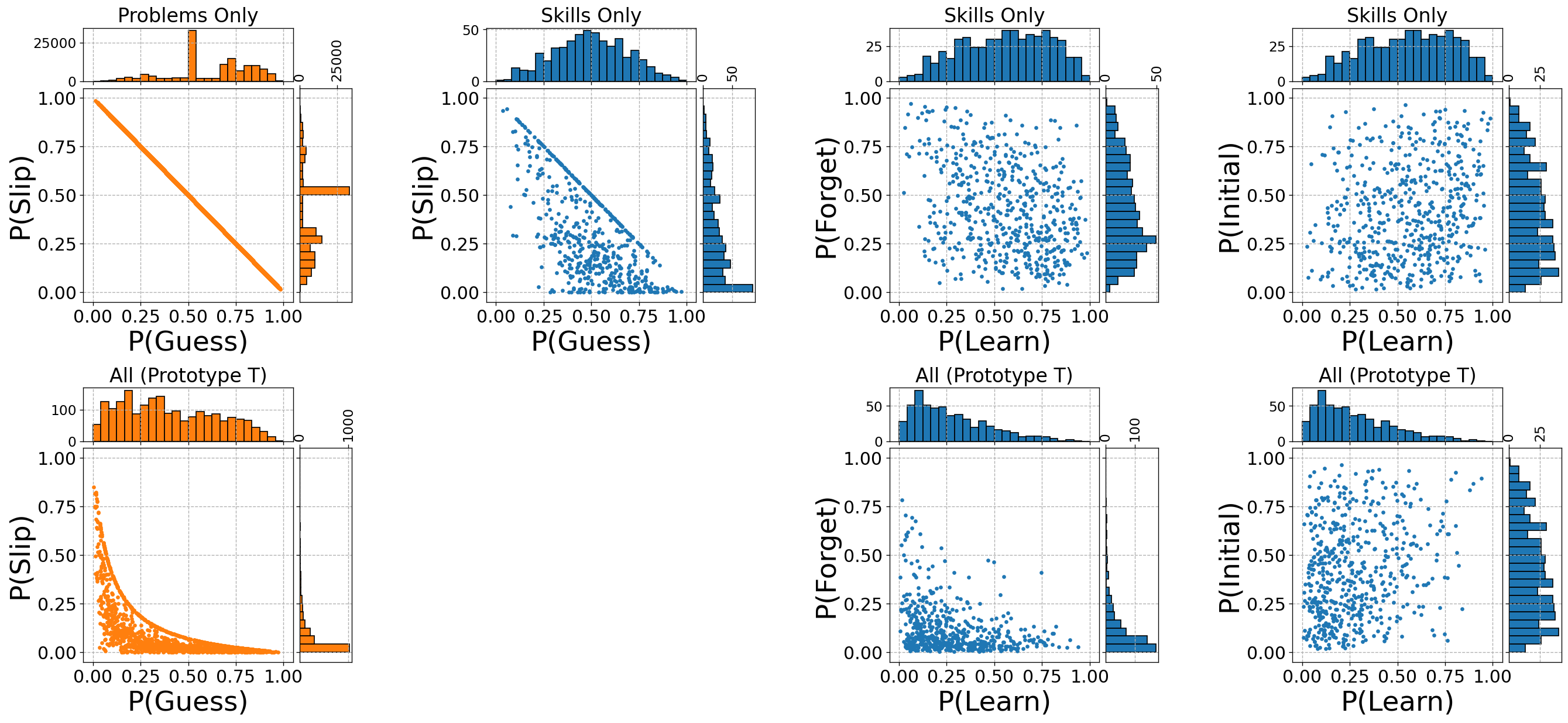
bridge_algebra06dataset. Blue and orange points correspond to
individual skills and problems, respectively. Problems Only corresponds to problem effects only,
Skills Only corresponds to skill effects only, and All corresponds to the combination of problem
effects, skill effects, and the most frequent prototype’s student effects (Prototype T).
As explained in the methodology, student effects in BKT+IRT are captured using learnable prototypes. We illustrate the top six discovered student prototypes and their frequency over the entire dataset in Figure 18a. The frequency of a prototype \(g\) is the number of students whose most likely prototype, after observing all of their trials, is \(g\). Prototypes are sorted according to their frequency, from smallest to largest. Note that the prototype letter only serves to identify the prototype and has no additional interpretation. We report not-slipping and not-forgetting probabilities, instead of slipping and forgetting, so that higher values of all four probabilities always correspond to more skilled students. As with the previous analyses, here we consider student effects in isolation, so the probabilities are calculated by setting skill and problem effects to zero. Prototype T is the most frequent and students belonging to it have guessing, slipping, learning, and forgetting probabilities of 0.23, 0.20, 0.18, and 0.10, respectively. The next most common prototype, S, has a significantly greater guessing probability (0.5), a smaller slip probability (0.11), and smaller learning and forgetting probabilities (0.15 and 0.06, respectively). Note that prototype S and R’s guess probability of \(\approx \) 0.5 corresponds to an offset \(\theta _u^G = 0\), so they do not contribute to their students’ guessing probabilities. Similarly, prototype P does not contribute to its students’ slipping probabilities.
Figure 18b shows the meaning of the parameter estimates in Figure 18a. At the top, the probability of knowing the KC over time \(P(s_t = 1)\) is plotted for each prototype, averaging over all skills (more frequent skills get weighed more). In the bottom, the probability of a correct answer \(P(y_t = 1)\) is plotted as a function of knowledge probability, averaging over all problems and skills by their frequency. Higher learning rates do not always correspond to higher knowledge probabilities by the end of the trial sequence. For example, Prototype O (brown) learns slightly more quickly than R (green) but saturates at a lower level. This is because O has a higher learning offset but a smaller not-forgetting offset than R. Prototype S (orange) is also slower to learn but ultimately catches up and slightly exceeds O for the same reason. In terms of predicted correctness, the relative ordering of prototypes changes, with O achieving the highest predicted correctness because of its high guessing and not-slipping offsets, whereas prototype R achieves lower performance because of a smaller not-slipping offset, and the fact that it does not contribute to the guessing probability. The blue line has the steepest slope, indicating that students belonging to prototype T achieve the biggest improvement in correctness when knowing the KC.


Similarly to the previous analysis, we can analyze the meaning of the parameters of selected KCs. KCs were filtered to exclude those with less than 5,000 trials in the dataset. Then, they were sorted by their maximum knowledge probability according to the model, \(\frac {p_L}{p_L + p_F}\). From this sorted list, 10 KCs were selected uniformly. Figure 19 plots the prior knowledge state trajectory, predicted correctness, and within-KC problem variability, for each selected KC. The trajectories and predicted correctness are obtained by taking a weighted average over all student prototypes and problems. The actual KC label is included, although the KC annotations in this dataset are not always clear. One of the most difficult skills to learn and answer is Write expression, any form: after 20 trials, the prior probability of knowing the skill is less than 0.5, and even then, the student only has a 75% chance of answering correctly. In contrast, most students do not start knowing the Identify fraction associated with each piece of a vertical bar skill, but they learn it quickly by the 5th opportunity, at which point they would have \(\approx \) 90% chance of answering the skill correctly. Identify LCM - one number multiple of other is an anomaly: it is very difficult to learn yet very easy to answer correctly on regardless of knowledge. The initial knowledge probability of that KC is greater than the maximum knowledge probability due to the KC’s high forgetting factor. However, students still have more than a 75% chance of answering correctly on the KC, regardless of whether they know it or not. This kind of anomaly could be resolved by placing extra constraints on the model. First, we can parameterize the initial knowledge probability such that it is always less than the maximum knowledge probability. Second, we can limit the guess and slip probabilities so that they do not exceed a certain threshold, such as 0.4 for example. Problem variability within the selected KCs is illustrated in the right panel of Figure 19. The x-axis is the guessing offset of problems within the KC (recall that the not-slipping offset for problems is the same as the guessing offset). Five out of 10 KCs have a 25% percentile that is greater than zero, indicating that problems within those KCs increase the guessing probability over the KC’s baseline probability. The Identify LCM skill has problems with logits that are reliably less than zero, indicating that they reduce the guessing probability relative to their KC’s baseline. All in all, the high variability of guessing probabilities indicates that problems within KCs in this dataset are not homogenous in terms of difficulty.
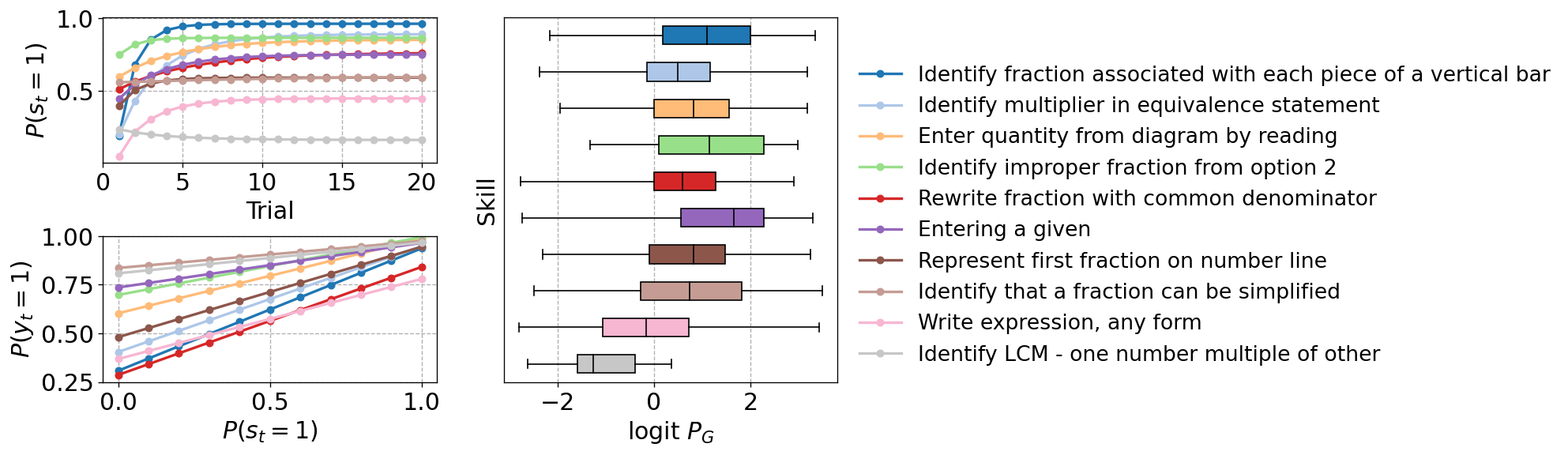
4.5.2. Exercise Selection
One of the reasons for using predictive models in tutoring systems is to select problems with the appropriate level of difficulty for the student. Both black-box and interpretable models can be used for this task. However, from a researcher’s or teacher’s perspective, it is important to understand why a scheduling algorithm selects a particular problem. Figure 20 shows how the prototype of the student in BKT+IRT modulates the guessing (left panel) and slipping probabilities (right panel) of the optimal problem to present at \(t+1\) (based on the Enter items numerator skill, which has 417 problems). The optimal problem here is defined as the one that the model predicts to be answered correctly with a probability of 0.75. For clarity, student prototypes were qualitatively labeled based on their parameter estimates in Figure 18: O is strong all-around, P is weak all-around, Q is strong but has weak dynamics, R and S are weak learners, but they don’t slip, and T is weak but doesn’t forget. Overall, when the student does not know the skill (\(P(s_t = 1|\mathbf {y}_{1:t})\) close to zero), the optimal problem will have high guessing and low slipping probabilities. As the probability of knowing the skill increases, the guessing and slipping probabilities decrease and increase, respectively. The following list highlights specific differences among prototypes:
- Strong versus weak students: Prototypes O (brown) and P (purple) are strong and weak all-around, respectively, so the optimal problem for the former will be harder than the latter (i.e., the problem will have smaller guessing and not-slipping offsets). Q is also strong but is less likely to learn and retain knowledge than O, so the algorithm presents Q with slightly easier problems than O.
- Forgetting: Prototypes T (blue) and P (purple) are both weak so they get assigned easier problems than the others. Both have similar guessing and learning offsets, so their optimal problems will be similar when the student’s knowledge probability is low. However, as that knowledge probability increases, the blue and purple curves diverge because T is less likely to forget than P, so it is more likely to know the KC at \(t+1\). Because of this, T will be assigned problems with higher slipping probabilities (right panel) and since the problem guessing and slipping probabilities are inversely related (Figure 17), T’s optimal problems will have smaller guessing probabilities than P’s.
- Slipping: Prototypes S (orange) and R (red) are both weak but don’t slip, so their optimal problems will be harder than those of P and T.
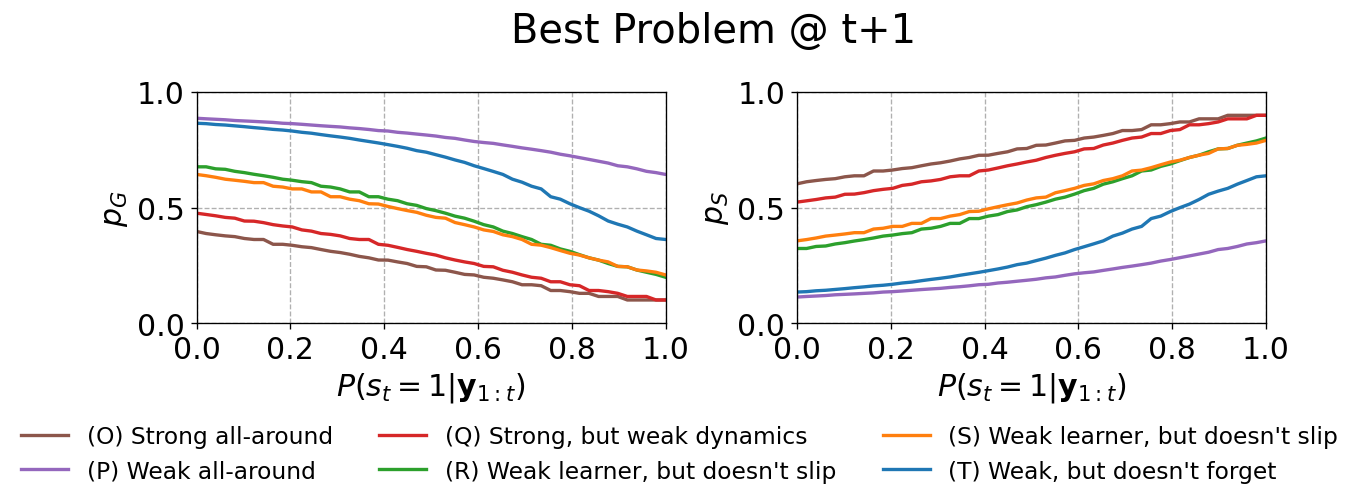
4.5.3. Visualizing Student Performance
BKT+IRT can be used to trace the student’s hidden knowledge state, just like BKT. Figure 21 digs into the performance of two students A and B (representing the lowest 1% and top 99% in terms of average correctness, respectively). The selected students practiced mostly different skill sets that overlapped in 21 skills only. Thus, we limited the visualization to focus on trials involving those overlapping skills. In the top row, a moving average with window size of 10% of total sequence length is used to display the response accuracy. The magenta line represents the average on those trials. The next row plots the smoothed estimates of the probability that the student knows each of the 21 skills. The last row shows the probabilities associated with the most likely student prototype (for visualization, probabilities are calculated assuming skill and problem effects are zero). The two students do not practice for the same number of trials (560 versus 101). Student B has greater guessing, learning, and not-slipping probabilities than student A. Both students have similar not-forgetting probabilities. By the end of the trial sequences, students A and B have a median knowledge probability of 0.16 and 0.50, respectively, indicating that student B has mastered more skills than student A.
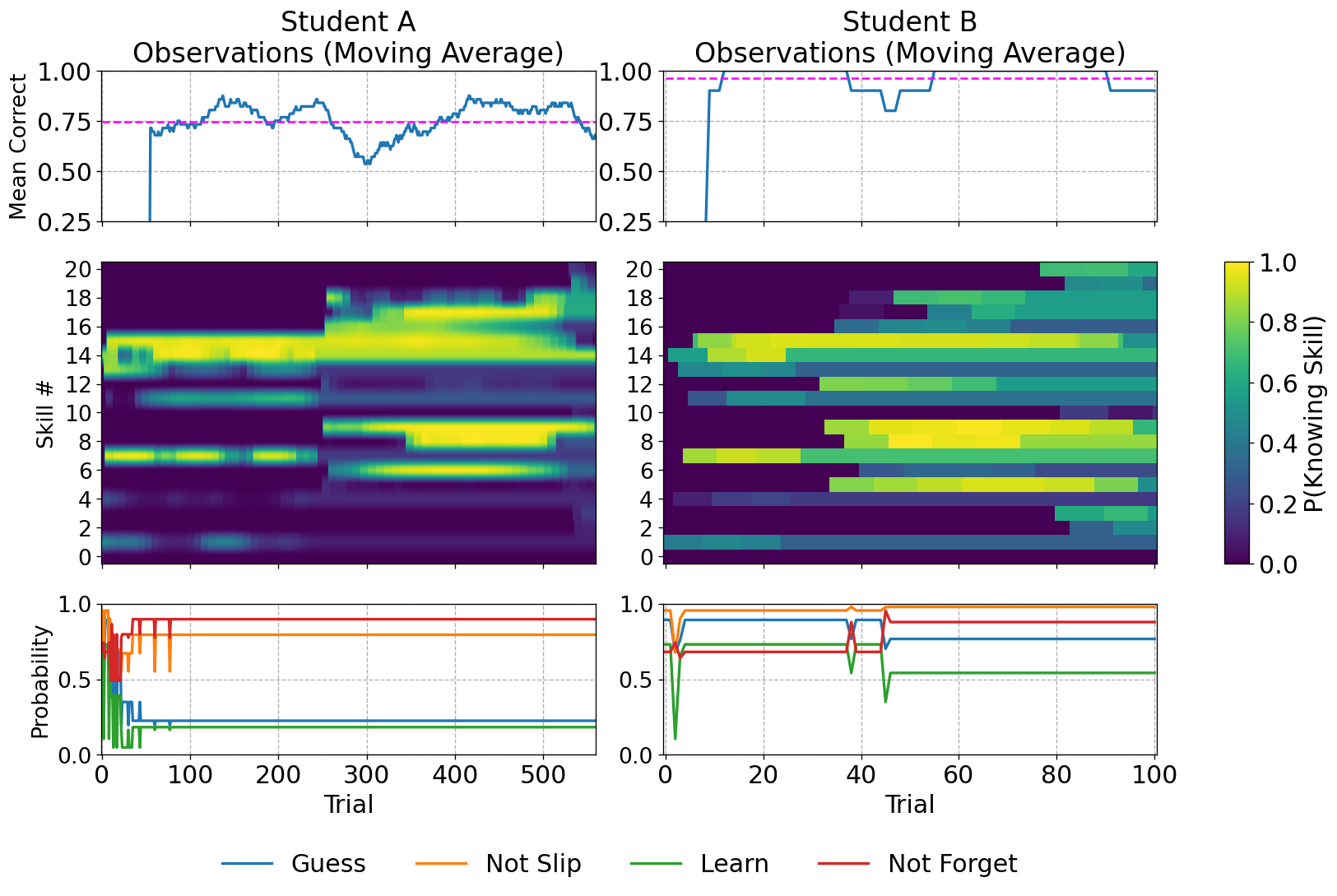
5. Conclusion
Bayesian Knowledge Tracing has always been trained with brute-force or custom fine-tuned expectation maximization or gradient descent training algorithms that limit the model’s utility and extensibility. Our contributions are three-fold: (a) efficient implementations of BKT RNN cells that could be easily extended and integrated with other NN modules, (b) a multidimensional BKT+IRT RNN model that can generalize to new students in a principled way, and (c) a skill discovery BKT RNN model that learns the problem-KC assignment matrix end-to-end.
Efficiency is achieved by leveraging first-order gradient descent optimizers in PyTorch and accelerated parallel processing capabilities of graphical processing units. The binary knowledge state of BKT also permits even more speedups by allowing the learning algorithm to process multiple trials in the sequence in parallel. Flexibility is possible due to PyTorch’s automatic symbolic differentiation capabilities which only require the modeler to specify the forward computation pass, leaving the complicated backward pass to the framework.
To demonstrate the flexibility of our implementations, two novel extensions to BKT were developed and evaluated. The first extension, multidimensional BKT+IRT, enables the model to contextualize predictions based on multidimensional problem and student parameters. Similar existing implementations of this model only use one ability dimension, which fails to capture situations such as students learning slowly and forgetting slowly, etc. Also, our implementation can generalize to new students in a principled way via the application of Bayes rule, unlike other implementations. In cases where the distribution of student abilities may differ from training to testing, we also demonstrate a more basic variant of the model which discretizes the ability values over a one-dimensional grid.
The second extension is the skill discovery BKT model which uses a novel multi-KC BKT RNN cell whose output is differentiable with respect to the problem-KC assignment matrix. This cell receives KC assignments from a stochastic NN layer that is parameterized by the problem-KC membership probabilities and can generate differentiable Q-matrices based on them. The model is also augmented with an auxiliary loss objective that guides it towards plausible KC sequences, as well as the ability to use problem features to contextualize the problem-KC assignment probabilities.
On large synthetic datasets, BKT RNN is within the same order of magnitude as an optimized implementation in terms of execution speed. The accelerated BKT RNN is even faster, achieving speedups of up to 47% over BKT RNN, depending on the size of the dataset. Both BKT RNN models recover the generating parameters of the synthetic datasets as well as, if not better than, the reference brute force model.
Thorough synthetic skill discovery experiments, where the true problem-KC assignments are known, show that the true order of KCs and their number in the dataset influences model performance. When KCs are structured in blocks, skill discovery models that use problem features as inputs can achieve high predictive accuracy while partially recovering the problem-KC assignment matrix. Guiding those models with the blocked-KC auxiliary loss improves their ability to recover that matrix even further. When the number of true KCs is small, this guidance almost fully recovers the true problem assignments. When KCs are interleaved, the task is much harder as it requires examining very long range dependencies. Nonetheless, for a moderate number of true KCs, using problem input features still provides high predictive accuracy and can recover about half of the maximum possible number of KCs. On real-world datasets, problem features enable the skill discovery model to match BKT with expert-provided skills in terms of accuracy. However there is tension between predictive performance and the KC recovery percentage, so there is room for improving our models in this regard. All in all, we recommend the inclusion of raw problem content in more EDM datasets as it does not require additional effort to collect (unlike skill annotations, which have to be created manually).
On real-world datasets, the multidimensional BKT+IRT model often performs the best out of all BKT extensions, and, in some cases, matches the performance of DKT. Indeed, except for one dataset, the best-performing BKT extension never lags DKT by more than 0.04 AUC-ROC points. The skill discovery model usually matches or exceeds the BKT+Problems model (these two models are comparable because they use the same set of information, skills and problems, but in different ways). However, when student effects are added to create the BKT+IRT model, skill discovery struggles to match it on most datasets.
BKT+IRT has well-defined parameters that interact with each other to generate predictions in a clear way. To demonstrate the model’s interpretability, we illustrated several visualizations of model parameters and their meaning from a dataset where BKT+IRT matches DKT and showed how student prototypes in BKT+IRT modulate the problem selection process.
There are several limitations to this work that could be addressed in the future:
- Static student abilities: student abilities in BKT+IRT and its multidimensional counterpart are assumed to be static: a student has an unknown fixed global ability level (or prototype) which the model tries to discover via sequential Bayesian updating. One extension to the model is to assume that student abilities evolve over time according to some temporal function, similar to the approach by Wilson et al. (2016). Our hypothesis is that this approach will not greatly improve BKT+IRT’s performance because BKT already has temporally evolving knowledge states (per skill).
- Lack of student effects in the skill discovery model: the absence of student effects likely hurt the model’s prediction ability on real-world datasets. Therefore, one future direction would be to include student effects in the form of unidimensional ability levels or multidimensional prototypes.
- Strong skill discovery performance requires problem representations: on synthetic datasets, strong skill discovery performance requires access to problem features or representations (though the model still does a good job on real-world datasets without problem representations). The situation is the same on the one real-world dataset we used that has problem features. And since the model uses high-dimensional problem features, there is always a risk of overfitting on small datasets. Therefore, one future direction is to develop a two-stage pipeline for skill discovery. The first stage consumes the dataset and outputs problem features (one naive representation of a problem is its correlation in terms of correctness with every other problem). The second stage would apply the skill discovery model with the representations learned from the first step.
- Rigid auxiliary loss: the auxiliary loss of the skill discovery model only favors blocked skill sequences, but one can imagine generalizing that loss to allow for other kinds of sequences, such as interleaving sequences. The auxiliary loss does not have to be related to sequence ordering either; it could for example encourage certain structures in the problem-skill matrix (e.g., skills should have a similar number of problems).
- Binary knowledge states: the standard BKT RNN code supports more than binary states and outputs, so a useful direction in the future would be to explore how increasing the number of states affects the developed extensions.
- Lack of hyperparameter optimization: no systematic hyperparameter optimization was performed on the developed BKT implementations, so extra predictive performance could be unlocked (e.g., batch sizes, learning rates, auxiliary loss coefficient, Gumbel-Softmax temperature, etc.). We left those out as we believe they are more relevant to production deployments where extracting every bit of performance is important.
- BKT parameter constraints: In vanilla BKT without forgetting, the student always gets better with successive opportunities a priori (probability of mastery monotonically increases). With forgetting, the probability of mastery will saturate at \(\frac {p_L}{p_L+p_F}\). Therefore, whether the student gets better with successive opportunities depends on their initial knowledge probability. If the initial knowledge probability is less than the saturation point, the student will get better and vice-versa. Thus, one way to improve the plausibility of the parameters of BKT with forgetting is to force the initial knowledge probability to be less than the saturation probability. Another related issue is to constrain the guessing and slipping offsets to be below certain thresholds so that knowing the KC is always guaranteed to significantly improve the likelihood of a correct answer. This is straightforward to do and left for future investigations.
- Student features: the flexibility of our models makes it easy to incorporate student features into the model. For example, in BKT+IRT the student’s GPA, prior academic achievements, etc. could be injected into the model via a linear neural network layer that outputs a distribution over student prototypes (e.g., a student’s GPA would determine which prototype they’d fall into). We have not looked into this as our datasets do not have such features.
- Skill discovery runtime: on large datasets, the SD model is orders of magnitude slower to train than the non-skill discovery models in this paper. The SD model cannot split the student’s trial sequence by skill as in BKT and BKT+IRT because the SD BKT cell has to be differentiable with respect to the problem-KC assignments. This is likely to be the reason behind the model’s poor training speed. Future investigations could look into modifications to allow the model to break trial sequences by skill whilst maintaining differentiability.
With the developed BKT RNNs and their extensions, we show that BKT still has its place amongst state-of-the-art student performance models, and can reap the same benefits that newer neural network models enjoy. The model’s implementation and all relevant code needed to reproduce the results of this work are available at our Github repository.
Funding
This work was conducted as part of Kuwait Institute for Scientific Research project SD011K.
References
- Ackerman, T. A. 1989. Unidimensional irt calibration of compensatory and noncompensatory multidimensional items. Applied Psychological Measurement 13, 2, 113–127.
- Anthony, L. and Ritter, S. 2008. Handwriting2/examples spring 2007.
- Bloom, B. S. 1984. The 2 sigma problem: The search for methods of group instruction as effective as one-to-one tutoring. Educational researcher 13, 6, 4–16.
- Boeck, P. D. and Wilson, M. 2004. Explanatory Item Response Models: a Generalized Linear and Nonlinear Approach. Springer-Verlag, New York, NY.
- Bradley, A. P. 1997. The use of the area under the roc curve in the evaluation of machine learning algorithms. Pattern Recogn. 30, 7 (jul), 1145–1159.
- Cen, H., Koedinger, K., and Junker, B. 2006. Learning factors analysis – a general method for cognitive model evaluation and improvement. In Intelligent Tutoring Systems, M. Ikeda, K. D. Ashley, and T.-W. Chan, Eds. Springer Berlin Heidelberg, Berlin, Heidelberg, 164–175.
- Corbett, A. T. and Anderson, J. R. 1994. Knowledge tracing: Modelling the acquisition of procedural knowledge. User modeling and user-adapted interaction 4, 4, 253–278.
- Dozat, T. 2016. Incorporating Nesterov Momentum into Adam. In Proceedings of the 4th International Conference on Learning Representations (2016). 1–4.
- Feng, M., Heffernan, N., and Koedinger, K. 2009. Addressing the assessment challenge with an online system that tutors as it assesses. User Modeling and User-Adapted Interaction 19, 3 (Aug 1,), 243–266.
- Finch, W. H. and French, B. F. 2018. Educational and psychological measurement. Routledge.
- Gervet, T., Koedinger, K., Schneider, J., Mitchell, T., et al. 2020. When is deep learning the best approach to knowledge tracing? Journal of Educational Data Mining 12, 3, 31–54.
- Ghosh, A., Heffernan, N., and Lan, A. S. 2020. Context-aware attentive knowledge tracing. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. KDD ’20. Association for Computing Machinery, New York, NY, USA, 2330–2339.
- Gonzalez-Brenes, J., Huang, Y., and Brusilovsky, P. 2014. General features in knowledge tracing to model multiple subskills, temporal item response theory, and expert knowledge. In The 7th International Conference on Educational Data Mining, J. C. Stamper, Z. A. Pardos, M. Mavrikis, and B. M. McLaren, Eds. International Educational Data Mining Society (IEDMS), 84 – 91.
- González-Brenes, J. P. and Mostow, J. 2012. Dynamic cognitive tracing: Towards unified discovery of student and cognitive models. In Proceedings of the 5th International Conference on Educational Data Mining, K. Yacef, O. R. Zaïane, A. Hershkovitz, M. Yudelson, and J. C. Stamper, Eds. International Educational Data Mining Society (IEDMS), 49–56.
- Goodfellow, I., Bengio, Y., and Courville, A. 2016. Deep learning. The MIT Press, London, England.
- Hochreiter, S. and Schmidhuber, J. 1997. Long short-term memory. Neural Computation 9, 8 (Nov 1,), 1735–1780.
- Hubert, L. and Arabie, P. 1985. Comparing partitions. Journal of classification 2, 1, 193–218.
- Jang, E., Gu, S., and Poole, B. 2017. Categorical reparameterization with gumbel-softmax. In 5th International Conference on Learning Representations (ICLR 2017). Curran Associates, Inc., 1920–1931.
- Jurafsky, D. and Martin, J. H. 2009. Speech and language processing, 2. ed., internat. ed. ed. Pearson Education International, Prentice Hall, Upper Saddle River.
- Khajah, M., Lindsey, R. V., and Mozer, M. 2016. How deep is knowledge tracing? In Proceedings of the 9th International Conference on Educational Data Mining, EDM 2016, T. Barnes, M. Chi, and M. Feng, Eds. International Educational Data Mining Society (IEDMS), 94–101.
- Khajah, M., Wing, R., Lindsey, R. V., and Mozer, M. 2014. Integrating latent-factor and knowledge-tracing models to predict individual differences in learning. In Proceedings of the 7th International Conference on Educational Data Mining, EDM 2014, J. C. Stamper, Z. A. Pardos, M. Mavrikis, and B. M. McLaren, Eds. International Educational Data Mining Society (IEDMS), 99–106.
- Koedinger, K. R., Carvalho, P. F., Liu, R., and McLaughlin, E. A. 2023. An astonishing regularity in student learning rate. Proceedings of the National Academy of Sciences 120, 13, e2221311120.
- Koedinger, K. R., Corbett, A. T., and Perfetti, C. 2012. The knowledge-learning-instruction framework: Bridging the science-practice chasm to enhance robust student learning. Cognitive Science 36, 5, 757–798.
- Koedinger, K. R., d. Baker, R. S. J., Cunningham, K., Skogsholm, A., Leber, B., and Stamper, J. 2010. A data repository for the edm community: The pslc datashop. In Handbook of Educational Data Mining, C. Romero, S. Ventura, M. Pechenizkiy, and R. S. Baker, Eds. CRC Press, Chapter 4, 43–56.
- Li, N., Cohen, W. W., and Koedinger, K. R. 2013. Discovering student models with a clustering algorithm using problem content. In Proceedings of the 9th International Conference on Educational Data Mining, EDM 2013, S. K. D’Mello, R. A. Calvo, and A. Olney, Eds. International Educational Data Mining Society (IEDMS), 98–105.
- Lindsey, R. V., Khajah, M., and Mozer, M. C. 2014. Automatic discovery of cognitive skills to improve the prediction of student learning. In Proceedings of the 27th International Conference on Neural Information Processing Systems - Volume 1, Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger, Eds. NIPS’14. MIT Press, Cambridge, MA, USA, 1386–1394.
- Lindsey, R. V., Shroyer, J. D., Pashler, H., and Mozer, M. C. 2014. Improving students’ long-term knowledge retention through personalized review. Psychological Science 25, 3, 639–647.
- Liu, R. and Koedinger, K. R. 2017. Closing the loop: Automated data-driven cognitive model discoveries lead to improved instruction and learning gains. Journal of Educational Data Mining 9, 1 (Sep.), 25–41.
- Martori, F., Cuadros, J., and González-Sabaté, L. 2015. Direct estimation of the minimum RSS value for training bayesian knowledge tracing parameters. In Proceedings of the 8th International Conference on Educational Data Mining, EDM 2015, Madrid, Spain, June 26-29, 2015, O. C. Santos, J. Boticario, C. Romero, M. Pechenizkiy, A. Merceron, P. Mitros, J. M. Luna, M. C. Mihaescu, P. Moreno, A. Hershkovitz, S. Ventura, and M. C. Desmarais, Eds. International Educational Data Mining Society (IEDMS), 364–367.
- Molnar, C. 2022. Interpretable Machine Learning, 2 ed.
https://christophm.github.io/interpretable-ml-book. - Montero, S., Arora, A., Kelly, S., Milne, B., and Mozer, M. 2018. Does deep knowledge tracing model interactions among skills? In Proceedings of the 11th International Conference on Educational Data Mining, EDM 2018, K. E. Boyer and M. Yudelson, Eds. International Educational Data Mining Society (IEDMS), 462–466.
- Pardos, Z. A. and Heffernan, N. T. 2010. Navigating the parameter space of bayesian knowledge tracing models: Visualizations of the convergence of the expectation maximization algorithm. In Educational Data Mining 2010, The 3rd International Conference on Educational Data Mining, R. S. J. de Baker, A. Merceron, and P. I. P. Jr., Eds. International Educational Data Mining Society (IEDMS), 161–170.
- Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J., and Chintala, S. 2019. Pytorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems 32. Curran Associates, Inc., 8024–8035.
- Pavlik, P. I., Cen, H., and Koedinger, K. R. 2009. Performance factors analysis –a new alternative to knowledge tracing. In Proceedings of the 2009 Conference on Artificial Intelligence in Education: Building Learning Systems That Care: From Knowledge Representation to Affective Modelling, V. Dimitrova, R. Mizoguchi, B. du Boulay, and A. Graesser, Eds. IOS Press, NLD, 531–538.
- Pelánek, R. 2014. Application of time decay functions and the elo system in student modeling. In Proceedings of the 7th International Conference on Educational Data Mining, EDM 2014, J. C. Stamper, Z. A. Pardos, M. Mavrikis, and B. M. McLaren, Eds. International Educational Data Mining Society (IEDMS), 21–27.
- Pelánek, R. 2017. Bayesian knowledge tracing, logistic models, and beyond: An overview of learner modeling techniques. User Modeling and User-Adapted Interaction 27, 3–5 (dec), 313–350.
- Pelánek, R. and Řihák, J. 2017. Experimental analysis of mastery learning criteria. In Proceedings of the 25th Conference on User Modeling, Adaptation and Personalization. UMAP ’17. Association for Computing Machinery, New York, NY, USA, 156–163.
- Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L. J., and Sohl-Dickstein, J. 2015. Deep knowledge tracing. Advances in Neural Information Processing Systems 28, 505–513.
- Ravand, H. and Robitzsch, A. 2018. Cognitive diagnostic model of best choice: a study of reading comprehension. Educational Psychology 38, 10, 1255–1277.
- Reckase, M. 2009. Multidimensional Item Response Theory. Statistics for Social and Behavioral Sciences. Springer New York.
- Reckase, M. D. 1979. Unifactor latent trait models applied to multifactor tests: Results and implications. Journal of Educational Statistics 4, 3, 207–230.
- Reimers, N. and Gurevych, I. 2019. Sentence-bert: Sentence embeddings using siamese bert-networks. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), K. Inui, J. Jiang, V. Ng, and X. Wan, Eds. Association for Computational Linguistics, Association for Computational Linguistics, 3980–3990.
- Ritter, S., Anderson, J. R., Koedinger, K. R., and Corbett, A. 2007. Cognitive tutor: Applied research in mathematics education. Psychonomic Bulletin & Review 14, 2, 249–255.
- Ritter, S., Harris, T. K., Nixon, T., Dickison, D., Murray, R. C., and Towle, B. 2009. Reducing the knowledge tracing space. In Educational Data Mining 2009: 2nd International Conference on Educational Data Mining, Proceedings, T. Barnes, M. C. Desmarais, C. Romero, and S. Ventura, Eds. International Educational Data Mining Society (IEDMS), 151–160.
- Stamper, J., Niculescu-Mizil, A., Ritter, S., Gordon, G., and Koedinger, K. 2010a.
Algebra i 2005-2006. development data set from kdd cup 2010 educational data mining challenge.
Find it at
http://pslcdatashop.web.cmu.edu/KDDCup/downloads.jsp. - Stamper, J., Niculescu-Mizil, A., Ritter, S., Gordon, G., and Koedinger, K. 2010b. Bridge
to algebra 2006-2007. development data set from kdd cup 2010 educational data mining challenge.
Find it at
http://pslcdatashop.web.cmu.edu/KDDCup/downloads.jsp. - Tsutsumi, E., Kinoshita, R., and Ueno, M. 2021. Deep-irt with independent student and item networks. In Proceedings of the 14th International Conference on Educational Data Mining, EDM 2021, S. I. Hsiao, S. S. Sahebi, F. Bouchet, and J. Vie, Eds. International Educational Data Mining Society (IEDMS), 510–517.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., and Polosukhin, I. 2017. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, U. von Luxburg, I. Guyon, S. Bengio, H. Wallach, and R. Fergus, Eds. NIPS’17. Curran Associates Inc., Red Hook, NY, USA, 6000–6010.
- Wilson, K. H., Karklin, Y., Han, B., and Ekanadham, C. 2016. Back to the basics: Bayesian extensions of IRT outperform neural networks for proficiency estimation. In Proceedings of the 9th International Conference on Educational Data Mining, EDM 2016, T. Barnes, M. Chi, and M. Feng, Eds. International Educational Data Mining Society (IEDMS), 539–544.
- Yao, L. and Schwarz, R. D. 2006. A multidimensional partial credit model with associated item and test statistics: An application to mixed-format tests. Applied psychological measurement 30, 6 (Nov), 469–492.
- Yeung, C.-K. 2019. Deep-irt: Make deep learning based knowledge tracing explainable using item response theory. arXiv preprint arXiv:1904.11738.
- Yudelson, M. 2022. A tool for fitting hidden markov models models at scale.
https://github.com/myudelson/hmm-scalable. - Zhang, J., Shi, X., King, I., and Yeung, D.-Y. 2017. Dynamic key-value memory networks for knowledge tracing. In Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 765–774.
Appendix
| Model | Dataset | AUC-ROC | ARI | % Shuffling | RI | % Recovered | % Recovered Limit | AUC-ROC Stderr | ARI Stderr | % Recovered Stderr |
|---|---|---|---|---|---|---|---|---|---|---|
| No SD | 5 KCs | 0.62 | nan | 0 | 0.00 | 0 | 100 | 0.01 | nan | 0.00 |
| Single KC | 5 KCs | 0.68 | nan | 0 | 0.00 | 0 | 100 | 0.02 | nan | 0.00 |
| SD | 5 KCs | 0.62 | 0.17 | 59 | 0.82 | 4 | 100 | 0.02 | 0.10 | 4.00 |
| SD+AuxLoss | 5 KCs | 0.70 | 0.52 | 26 | 0.75 | 36 | 100 | 0.02 | 0.18 | 19.39 |
| SD+Rep | 5 KCs | 0.71 | 0.70 | 18 | 0.92 | 56 | 100 | 0.02 | 0.08 | 7.48 |
| SD+AuxLoss+Rep | 5 KCs | 0.74 | 0.95 | 2 | 0.98 | 92 | 100 | 0.01 | 0.05 | 8.00 |
| Clustering | 5 KCs | 0.64 | 0.35 | 42 | 0.86 | 0 | 100 | 0.01 | 0.00 | 0.00 |
| No SD | 25 KCs | 0.66 | nan | 0 | 0.00 | 0 | 76 | 0.00 | nan | 0.00 |
| Single KC | 25 KCs | 0.68 | nan | 0 | 0.00 | 0 | 76 | 0.00 | nan | 0.00 |
| SD | 25 KCs | 0.65 | 0.07 | 71 | 0.92 | 0 | 76 | 0.00 | 0.01 | 0.00 |
| SD+AuxLoss | 25 KCs | 0.70 | 0.48 | 22 | 0.93 | 23 | 76 | 0.01 | 0.03 | 2.94 |
| SD+Rep | 25 KCs | 0.70 | 0.45 | 24 | 0.94 | 21 | 76 | 0.00 | 0.03 | 5.15 |
| SD+AuxLoss+Rep | 25 KCs | 0.70 | 0.63 | 12 | 0.96 | 35 | 76 | 0.01 | 0.02 | 2.33 |
| Clustering | 25 KCs | 0.69 | 0.59 | 14 | 0.96 | 40 | 76 | 0.00 | 0.00 | 0.00 |
| No SD | 50 KCs | 0.67 | nan | 0 | 0.00 | 0 | 38 | 0.00 | nan | 0.00 |
| Single KC | 50 KCs | 0.64 | nan | 0 | 0.00 | 0 | 38 | 0.03 | nan | 0.00 |
| SD | 50 KCs | 0.66 | 0.04 | 73 | 0.91 | 0 | 38 | 0.01 | 0.00 | 0.00 |
| SD+AuxLoss | 50 KCs | 0.70 | 0.35 | 18 | 0.94 | 8 | 38 | 0.00 | 0.01 | 1.10 |
| SD+Rep | 50 KCs | 0.69 | 0.19 | 38 | 0.92 | 3 | 38 | 0.00 | 0.02 | 0.49 |
| SD+AuxLoss+Rep | 50 KCs | 0.69 | 0.36 | 16 | 0.94 | 12 | 38 | 0.00 | 0.01 | 1.79 |
| Clustering | 50 KCs | 0.69 | 0.32 | 20 | 0.95 | 8 | 38 | 0.00 | 0.00 | 0.00 |
| Model | Dataset | AUC-ROC | ARI | % Shuffling | RI | % Recovered | % Recovered Limit | AUC-ROC Stderr | ARI Stderr | % Recovered Stderr |
|---|---|---|---|---|---|---|---|---|---|---|
| No SD | 5 KCs | 0.61 | nan | 0 | 0.00 | 0 | 100 | 0.01 | nan | 0.00 |
| Single KC | 5 KCs | 0.51 | nan | 0 | 0.00 | 0 | 100 | 0.00 | nan | 0.00 |
| SD | 5 KCs | 0.60 | 0.08 | 73 | 0.79 | 0 | 100 | 0.02 | 0.02 | 0.00 |
| SD+AuxLoss | 5 KCs | 0.53 | -0.00 | 95 | 0.63 | 0 | 100 | 0.01 | 0.02 | 0.00 |
| SD+Rep | 5 KCs | 0.73 | 0.71 | 18 | 0.92 | 48 | 100 | 0.01 | 0.04 | 4.90 |
| SD+AuxLoss+Rep | 5 KCs | 0.59 | 0.26 | 46 | 0.62 | 8 | 100 | 0.02 | 0.03 | 4.90 |
| Clustering | 5 KCs | 0.64 | 0.35 | 42 | 0.86 | 0 | 100 | 0.01 | 0.00 | 0.00 |
| No SD | 25 KCs | 0.66 | nan | 0 | 0.00 | 0 | 76 | 0.00 | nan | 0.00 |
| Single KC | 25 KCs | 0.51 | nan | 0 | 0.00 | 0 | 76 | 0.00 | nan | 0.00 |
| SD | 25 KCs | 0.66 | 0.07 | 71 | 0.91 | 0 | 76 | 0.00 | 0.01 | 0.00 |
| SD+AuxLoss | 25 KCs | 0.60 | 0.20 | 48 | 0.88 | 0 | 76 | 0.00 | 0.04 | 0.00 |
| SD+Rep | 25 KCs | 0.70 | 0.55 | 18 | 0.96 | 36 | 76 | 0.00 | 0.03 | 6.62 |
| SD+AuxLoss+Rep | 25 KCs | 0.57 | 0.18 | 53 | 0.80 | 0 | 76 | 0.01 | 0.01 | 0.00 |
| Clustering | 25 KCs | 0.68 | 0.59 | 14 | 0.96 | 40 | 76 | 0.00 | 0.00 | 0.00 |
| No SD | 50 KCs | 0.67 | nan | 0 | 0.00 | 0 | 38 | 0.00 | nan | 0.00 |
| Single KC | 50 KCs | 0.51 | nan | 0 | 0.00 | 0 | 38 | 0.00 | nan | 0.00 |
| SD | 50 KCs | 0.66 | 0.03 | 75 | 0.92 | 0 | 38 | 0.00 | 0.00 | 0.00 |
| SD+AuxLoss | 50 KCs | 0.59 | 0.16 | 42 | 0.91 | 0 | 38 | 0.00 | 0.02 | 0.80 |
| SD+Rep | 50 KCs | 0.67 | 0.20 | 36 | 0.94 | 2 | 38 | 0.00 | 0.01 | 0.75 |
| SD+AuxLoss+Rep | 50 KCs | 0.58 | 0.15 | 46 | 0.86 | 0 | 38 | 0.01 | 0.02 | 0.00 |
| Clustering | 50 KCs | 0.67 | 0.32 | 20 | 0.95 | 8 | 38 | 0.00 | 0.00 | 0.00 |
| Model | Dataset | AUC-ROC | ARI | % Shuffling | RI | % Recovered | % Recovered Limit | AUC-ROC Stderr | ARI Stderr | % Recovered Stderr |
|---|---|---|---|---|---|---|---|---|---|---|
| No SD | bridge_algebra06 | 0.61 | nan | 0 | 0.00 | 0 | 54 | 0.00 | nan | 0.00 |
| Single KC | bridge_algebra06 | 0.55 | nan | 0 | 0.00 | 0 | 54 | 0.01 | nan | 0.00 |
| SD | bridge_algebra06 | 0.61 | 0.00 | 95 | 0.97 | 0 | 54 | 0.00 | 0.00 | 0.00 |
| SD+AuxLoss | bridge_algebra06 | 0.55 | 0.00 | 100 | 0.97 | 0 | 54 | 0.00 | 0.00 | 0.00 |
| SD+Rep | bridge_algebra06 | 0.68 | 0.37 | 32 | 0.97 | 6 | 54 | 0.00 | 0.01 | 1.28 |
| SD+AuxLoss+Rep | bridge_algebra06 | 0.60 | 0.02 | 87 | 0.40 | 11 | 54 | 0.00 | 0.01 | 1.36 |
| Clustering | bridge_algebra06 | 0.63 | 0.61 | 12 | 0.99 | 37 | 54 | 0.00 | 0.02 | 1.09 |
| No SD | statics | 0.62 | nan | 0 | 0.00 | 0 | 92 | 0.00 | nan | 0.00 |
| Single KC | statics | 0.54 | nan | 0 | 0.00 | 0 | 92 | 0.01 | nan | 0.00 |
| SD | statics | 0.61 | 0.02 | 95 | 0.75 | 0 | 92 | 0.00 | 0.00 | 0.00 |
| SD+AuxLoss | statics | 0.55 | 0.01 | 97 | 0.75 | 0 | 92 | 0.00 | 0.00 | 0.00 |
| SD+Rep | statics | 0.65 | 0.42 | 44 | 0.83 | 11 | 92 | 0.00 | 0.04 | 0.35 |
| SD+AuxLoss+Rep | statics | 0.57 | 0.47 | 40 | 0.74 | 48 | 92 | 0.00 | 0.00 | 0.02 |
| Clustering | statics | 0.63 | 0.10 | 83 | 0.77 | 10 | 92 | 0.00 | 0.00 | 0.00 |
| No SD | assistments09 | 0.63 | nan | 0 | 0.00 | 0 | 73 | 0.00 | nan | 0.00 |
| Single KC | assistments09 | 0.62 | nan | 0 | 0.00 | 0 | 73 | 0.02 | nan | 0.00 |
| SD | assistments09 | 0.63 | 0.01 | 93 | 0.96 | 0 | 73 | 0.00 | 0.00 | 0.00 |
| SD+AuxLoss | assistments09 | 0.68 | 0.17 | 55 | 0.96 | 0 | 73 | 0.00 | 0.01 | 0.00 |
| SD+Rep | assistments09 | 0.71 | 0.46 | 24 | 0.97 | 19 | 73 | 0.00 | 0.00 | 0.75 |
| SD+AuxLoss+Rep | assistments09 | 0.66 | 0.05 | 77 | 0.53 | 10 | 73 | 0.00 | 0.02 | 1.48 |
| Clustering | assistments09 | 0.66 | 0.70 | 6 | 0.99 | 48 | 73 | 0.00 | 0.02 | 2.24 |
| Model | algebra05 | assistments09 | assistments12 | assistments15 | assistments17 | bridge_algebra06 | spanish | statics |
|---|---|---|---|---|---|---|---|---|
| BKT | 0.76 | 0.71 | 0.68 | 0.69 | 0.64 | 0.76 | 0.83 | 0.70 |
| BKT+Abilities | 0.77 | 0.73 | 0.69 | 0.70 | 0.65 | 0.74 | 0.85 | 0.70 |
| BKT+Problems | 0.79 | 0.71 | 0.70 | 0.66 | 0.67 | 0.75 | 0.84 | 0.79 |
| BKT+IRT | 0.81 | 0.75 | 0.73 | 0.69 | 0.70 | 0.76 | 0.86 | 0.81 |
| BKT+IRT (Multidim) | 0.82 | 0.75 | 0.72 | 0.70 | 0.70 | 0.78 | 0.86 | 0.81 |
| SD | 0.75 | 0.73 | 0.73 | 0.70 | 0.69 | 0.75 | 0.83 | 0.80 |
| DKT-Best | 0.82 | 0.76 | 0.77 | 0.73 | 0.77 | 0.78 | 0.83 | 0.83 |
| Absolute Best | 0.83 | 0.77 | 0.77 | 0.73 | 0.77 | 0.80 | 0.86 | 0.83 |
| Prototype | Frequency | p_G | p_NS | p_L | p_NF |
|---|---|---|---|---|---|
| O | 0.02 | 0.74 | 0.96 | 0.26 | 0.89 |
| P | 0.03 | 0.20 | 0.55 | 0.16 | 0.78 |
| Q | 0.07 | 0.68 | 0.95 | 0.15 | 0.81 |
| R | 0.16 | 0.47 | 0.89 | 0.18 | 0.95 |
| S | 0.26 | 0.51 | 0.89 | 0.15 | 0.94 |
| T | 0.37 | 0.23 | 0.80 | 0.18 | 0.90 |
| KC | Min | Q1 | Median | Q3 | Max |
|---|---|---|---|---|---|
| Identify fraction associated with each piece of a vertical bar | -2.16 | 0.18 | 1.09 | 2.00 | 3.34 |
| Identify multiplier in equivalence statement | -2.38 | -0.14 | 0.48 | 1.16 | 3.18 |
| Enter quantity from diagram by reading | -1.95 | 0.00 | 0.82 | 1.56 | 3.18 |
| Identify improper fraction from option 2 | -1.33 | 0.09 | 1.14 | 2.27 | 2.97 |
| Rewrite fraction with common denominator | -2.78 | 0.00 | 0.59 | 1.27 | 2.90 |
| Entering a given | -2.74 | 0.56 | 1.66 | 2.28 | 3.30 |
| Represent first fraction on number line | -2.31 | -0.10 | 0.82 | 1.48 | 3.24 |
| Identify that a fraction can be simplified | -2.49 | -0.27 | 0.73 | 1.82 | 3.49 |
| Write expression, any form | -2.80 | -1.07 | -0.17 | 0.72 | 3.43 |
| Identify LCM - one number multiple of other | -2.62 | -1.59 | -1.26 | -0.40 | 0.36 |