Abstract
Learnersourcing is the process by which students submit content that enriches the bank of learning materials available to their peers, all as an authentic part of their learning experience. One example of learnersourcing is Technology-Mediated Peer Instruction (TMPI), whereby students are prompted to submit explanations to justify their choice in a multiple-choice question (MCQ), and are subsequently presented with explanations written by their peers, after which they can reconsider their own answer. TMPI allows students to contrast their reasoning with a variety of peer-submitted explanations. It is intended to foster reflection, ultimately leading to better learning. However, not all content submitted by students is adequate and it must be curated, a process that can require a significant effort by the teacher. The curation process ought to be automated for learnersourcing in TMPI to scale up to large classes, such as MOOCs. Even for smaller settings, automation is critical for the timely curation of student-submitted content, such as within a single assignment, or during a semester. We adapt methods from argument mining and natural language processing to address the curation challenge
and assess the quality of student answers submitted in TMPI, as judged by their peers. The curation task is
confined to the prediction of argument convincingness: an explanation submitted by a learner is considered of
good quality, if it is convincing to their peers. We define a methodology to measure convincingness scores using
three methods, Bradley-Terry, Crowd-Bradley-Terry and WinRate. We assess the performance of feature-rich
supervised learning algorithms as well as transformer-based neural approach to predict convincingness using
these scores. Experiments are conducted over different domains, from ethics to STEM. While the neural approach
shows the greatest correlation between its prediction and the different convincingness measures,
results show that success on this task is highly dependent on the domain and the type of question.
Keywords
Abstract
1. Introduction
Peer Instruction (PI) is a classroom-based activity, often mediated by automated response systems (e.g. clickers), wherein teachers prompt students to answer a Multiple-Choice Question (MCQ) individually, then break out into small groups and discuss their reasoning. Next, the student is offered a second opportunity to answer the same question. Research has shown that students demonstrate significant learning gains from the intermediate interaction with their peers (Crouch and Mazur, 2001). Synchronous, classroom-based PI is an effective component in the teaching practice of instructors looking to drive student engagement as part of an active learning experience (Charles et al., 2015). In discussing with peers after they have formulated their own reasoning, students are engaged in a higher order thinking, as they evaluate (Highest on Bloom’s taxonomy, Bloom et al. 1956) what is the strongest argument before answering again.
Prompting students to explain their reasoning is beneficial to their learning (Chi et al., 1994). Deliberate practice of argumentation in defence of one’s ideas has been shown to improve informal reasoning for science students (Venville and Dawson, 2010). There exists empirical evidence on the positive relationship between constructing formally sound arguments and deep cognitive elaboration, as well as the individual acquisition of knowledge (Stegmann et al., 2012).
Technology-mediated peer instruction (TMPI) platforms (Charles et al., 2019, University of British Columbia, 2019) augment MCQ items into a two-step process. It first prompts students for their answer choice, giving them an opportunity to explain their reasoning with a written open response. Second, student have a chance to compare and contrast their explanations with their peers.
On the first step, students must not only must choose an answer choice, but also provide an explanation that justifies their reasoning, as shown in figure 1a. On the second step (figure 1b), students are prompted to revise their answer choice by taking into consideration a subset of explanations written by their peers and choose the explanation they consider the most convincing.
In an MCQ context, the student will choose an explanation that falls within one of three scenarios according to whether the choice corresponds to the original answer choice and, if it does, whether it is their original explanation:
- 1.
- Different answer choice. Change their answer choice, by indicating which of their peer’s explanations for a different answer choice they find most convincing.
- 2.
- Same answer choice, different explanation. Keep the same answer choice, but indicate which of their peers’ explanations they deem more convincing than their own.
- 3.
- Same answer choice, same explanation. Choose “I stick to my own”, which indicates that they are keeping to the same answer choice, and that their own explanation is best from among those shown.
Whenever the student chooses either of the first two scenarios above, we frame this as “casting a
vote” for the peer explanation selected. By this vote, we will consider that the student has judged their
peer’s explanation as more convincing than their own explanation.
The panel on the right, figure 1(b), shows the
second review step of TMPI. The student can
reconsider their answer choice with a subset
of explanations written by previous students.
A set of peer-explanations is shown, one for
the student’s own answer choice, and another
set is shown for a different answer choice
(the correct answer if the student’s choice was
wrong, otherwise a randomly chosen incorrect
choice).
1.1. On convincingness and TMPI
As defined above, a more convincing explanation might be an incorrect answer. As such, we could question in what sense would convincingness help curate peer-submitted explanations?
One answer to this question is that incorrect explanations may nevertheless be useful for nurturing student reflection, such as better understanding what was a misleading reasoning. They also afford teachers the opportunity to mitigate the “expert blind spot” (Nathan et al., 2001), addressing student misconceptions they might not otherwise have thought of.
Another answer is that it is an intermediate step towards a better measure: the expected learning gain for a given explanation. Indeed, in TMPI environments, we aim to offer explanations that will bring the student to better understand the concepts and theories behind questions. Therefore, the ideal measure we would like to extract is the expected learning gain for each explanation. However, learning gains is a complex measure to obtain for several reasons:
- TMPI environments generally cover many skills and topics. A switch of topics and a variation in difficulty during item sequencing can induce a change in student performance that gets confounded with learning gains.
- Question items often involve more than one skill, as do explanations. As learning gains must be attributed to a specific skill or concept, it is difficult to untangle the correct imputation in multi-skill explanation pairs, for multi-skill questions.
- The exact “eureka!” moment often cannot precisely be established, blurring the timeline of the learning gain.
- The learning gain may not depend solely on the explanation, but also on the alternative explanations shown, a particular student’s misunderstanding, the specific sequencing of question items, etc.
- Explanations are only shown once per student, taking away the possibility of eliminating inter-student variance or explanatory factors.
Therefore, our aim at this stage of our research, and research on TMPI in general, is to solely derive a metric we call “convincingness in TMPI” defined as the propensity a student to select an explanation over others. This definition is closely linked to the notion of argument quality (Bentahar et al., 2010, Gretz et al., 2020, Wachsmuth et al., 2017) and for our purpose here could be considered interchangeable. However, it ought not be conflated with the notion of correctness. An argument can be convincing and of high quality, in the sense of scoring high on many features that characterize the quality of arguments such as being well structured, yet it can be incorrect.
1.2. Overview
The ultimate objectives of our research can be summarized in figure 2, which gives a schematic overview of how data from TMPI can be managed and leveraged to help curate peer explanations. We decompose this into a three-step process, as shown in figure 2. Firstly, in step (b), blatantly off-task student submissions must be filtered out. Automatic methods for this first-level of content moderation in TMPI are discussed in Gagnon et al. (2019) but are limited to ensuring that the irrelevant, potentially malicious student submissions are flagged and excluded from the database.
Second, the student votes must be aggregated in step (c) of figure 2. This rank aggregation will yield a globally ordered list of explanations for each question prompt, as in step (d). We can then use this global ranked list to select the subset which will be shown to future students (step (e)).
The third step is to mitigate the disproportionate impact of “early voters”: as soon as the first few students submit convincing explanations, it can become difficult for the explanations of “newer” students to be shown often enough to earn votes, and climb the ranks. Linguistic features can help mitigate this impact.
In step (g) of figure 2, feature-rich linguistic models are trained on a regression task, where the target is the aggregate rank score of student explanations seen thus far (see section 4.2). Such features can be lexical and statistical, syntatic, or semantic (in particular, involving embeddings extracted with neural models). Models able to correctly predict the relative convincingness of student explanations, based on the linguistic features, can help navigate the trade-off between exploiting the content that has already been shown to be of high quality, while exploring the possible effectiveness of newly submitted work. Such models can also help eliminate “cold-start” associated problems that occur when a new question item is introduced and no vote-data has yet been collected.
How the final ranking for the selection of explanations is computed (steps (d) and (e)) remains an open question, but we can assume it can be a learned process that combines input source rankings from (g) and (c). That process can take the form of a supervised learning task given the ground truth from (f), or the form a reinforcement learning task based on a deferred measure of learning gains, for example.
The problem of aggregating the results of evaluative peer judgments extends beyond TMPI. For example, in response to the difficulty students can have providing a holistic score to their peers’ work, there is a growing number of peer-review platforms built on comparative judgments. Notable examples include ComPAIR (Potter et al., 2017) and JuxtaPeer (Cambre et al., 2018), both of which present students with a pair of their peers’ submissions, and prompt the learner to evaluate them with respect to one another. As in TMPI, students apply a comparative judgment to only the subset of peer content that they are shown during the review step. There is a need for a principled approach to aggregating this learnersourced data, in a pedagogically relevant manner, despite the inevitable absence of an absolute pointwise ranking.
1.3. Research questions
Given the above considerations, we turn to our central research questions:
- Since each student’s “vote” in this context represents a pairwise judgment relative to other explanations, which rank aggregation methods are best suited for estimating global, pointwise ranking of the convincingness of student explanations in TMPI?
- Once we establish a global ranked list of explanations along the dimension of convincingness, can we model this construct and identify the linguistic features of the most effective student explanations, as judged by their peers?
We suggest that the results of our work can inform the design of technology-mediated peer instruction platforms. Such platforms will likely have an architecture analogous to figure 2’s, and thus have similar design objectives, which our work helps to address.
The first objective of this work is to provide feedback to learners: feedback that helps them better understand the characteristics common to the most convincing arguments in their discipline, promote learning, and develop critical reasoning skills.
The second objective is providing support to teachers: in such platforms, the amount of data generated scales very quickly. The data associated with each student-item pair includes many relevant variables: correct answer choice on first attempt, student explanation, subset of explanations shown, time spent writing and reading explanations, correct answer on second attempt, and the peer-explanation chosen as most convincing (see figure 4). This amount of information can be overwhelming for instructors who use such tools regularly as part of formative assessment. Automatically identifying the highest (and lowest) quality student explanations, as judged by other students, can support instructors in providing timely feedback.
A third related objective is to maintain the integrity of such platforms: automatic filtering of irrelevant/malicious student explanations is paramount to keep from being shown to future students (Gagnon et al., 2019), a non-trivial task for content written in natural language.
From here, we provide an overview of related research in learnersourcing of student explanations, automatic short-answer grading, and argument quality ranking (section 2). We then describe our TMPI dataset, as well as publicly available reference datasets of argument quality, which we use to evaluate our methodology (section 3).
The specific contributions made by this work include:
- proposing a methodology for evaluating the quality of student explanations, along the dimension of convincingness, in TMPI environments. An extension of previous work in Bhatnagar et al. (2020b), we demonstrate this methodology in section 4 and propose evaluation metrics based on practical issues in TMPI environments;
- a comprehensive evaluation of this proposed methodology using data from a real, live TMPI environment, with question items from multiple disciplines. We refine work from argument mining research and propose the use of consistent rank aggregation methods independent of model architecture;
- a comparison of feature-rich linguistic regression models with neural transformer-based models for the prediction of real-valued convincingness scores. We identify some of the linguistic features most often associated with high-quality student explanations in TMPI and the question types where predicting the convincingness of student explanations is more challenging. We also demonstrate how to leverage transfer learning from large pre-trained neural models for this task (section 5).
2. Related Work
2.1. Learnersourcing student explanations
TMPI is a specific case of learnersourcing, wherein students first generate content, and then help curate the content base, all as part of their learning process (Singh et al., 2022, Weir et al., 2015). Notable examples include PeerWise (Denny et al., 2008), Elaastic (Gomis and Silvestre, 2021, Silvestre et al., 2015) and RiPPLE (Khosravi et al., 2019), where students generate learning resources, which are subsequently used and evaluated by peers as part of formative assessment activities.
One of the earliest efforts specifically leveraging peer judgments of peer-written explanations is from the AXIS system (Williams et al., 2016), wherein students solved a problem, provided an explanation for their answer, and evaluated explanations written by their peers. Using a reinforcement-learning approach known as “multi-armed bandits”, the system could select peer-written explanations rated as helpful as those of an expert. The novel scheme proposed by Kolhe et al. (2016) also applies the potential of learnersourcing to the task of short answer grading: short answers submitted by students are evaluated by “future” peers in the context of multiple-choice questions, where the answer options are the short answers submitted by their “past” counterparts. Our research follows from these studies and focuses on how to use vote data more directly to model argument quality as judged by peers.
2.2. Automated Writing Evaluation
A central objective of our work is to evaluate the quality of student explanations in TMPI. Under the hierarchy of automated grading methods proposed by Burrows et al. (2015), this task falls under the umbrella of automatic short-answer grading (ASAG), where students must recall knowledge and express it in their own way, using natural language, typically between 10-100 words. Their in-depth historical review of ASAG systems describes a shifting focus in methods, from matching patterns derived from answers written by experts, to machine-learning approaches, with n-grams and hand-crafted features combined as input to supervised learning algorithms, such as decision trees and support vector machines.
For example, Mohler et al. (2011) measure alignment between dependency parse tree structures of student answers with those of an expert answer. These alignment features are paired with lexical semantic similarity features that are both knowledge-based (e.g. using WordNet) and corpus-based (e.g. Latent Semantic Analysis), and used as input to support vector machines which learn to grade short answers automatically. Another similar system proposed by Sultan et al. (2016) starts with features measuring lexical and contextual alignment between similar word pairs from student answers and a reference answer, as well as semantic vector similarity using “off-the-shelf” word embeddings. They then augment their input with “domain-specific” term-frequency and inverse document-frequency weights, to achieve their best results on several ASAG datasets using various validation schemes.
While modelling the quality of TMPI explanations has much in common with the ASAG task and can benefit from the features and methods borrowed from the systems mentioned above, a fundamental difference lies in how similarity to an expert explanation may not be the only appropriate reference. The “quality” we are measuring is that which is observed by a group of peers, which may be quite different from how a teacher might explain a concept.
Previous work on the automated evaluation of long-form persuasive essays (Ghosh et al., 2016, Klebanov et al., 2016, Nguyen and Litman, 2018) focused on modelling the pointwise scores given by experts. While our work here does not set out to “grade” student explanations, its aim is also to provide a pointwise estimate of the convincingness score out of pairwise data.
2.3. Ranking Arguments for Quality
Argument mining is a broad research area concerned with automatically identifying argumentative structures in free-text (e.g. claims and premises), classifying their pro/con stance with respect to the topic, and evaluating argument quality.
Modelling argument “quality” is an active sub-area of research, with direct applications in education, such as in automated scoring of persuasive essays written by students (Persing and Ng, 2015, Nguyen and Litman, 2018). In work more closely tied with peer instruction, it has been found that when students are asked to debate in dyads, there is a relationship between knowledge acquisition and the quality of arguments the students produce, as measured by the presence of formal argumentative structures (e.g. claims, premise, etc.) (Garcia-Mila et al., 2013).
In a comprehensive survey of research on the assessment of argument quality, a taxonomy of major quality dimensions for natural language arguments was proposed, with three principal aspects: logic, rhetoric, and dialect (Wachsmuth et al., 2017). As students vote on their peers’ explanations in TMPI, they may be evaluating the logical cogency (e.g. is this argument sound?), or its rhetorical quality (e.g. is this argument phrased well?). However, experiments have also shown that the perceived quality of an argument can depend on the audience (Mercier and Sperber, 2011). These foundational questions are out of the scope of this current study and the subject of future work.
Instead, we focus on modelling the aggregate quality rankings of student explanations based on their individual, pairwise vote data, and cast this along the dialectic dimension of argument quality, as convincingness. We suggest that the pairwise “vote” data collected in TMPI is a proxy for argument quality, along the dimension of convincingness, as judged by peer learners.
The current work moves from the pairwise prediction task to a point-wise regression. This is a field of study that is gaining attention in the research community, likely due to the fact that it spans a large array of applications beyond TMPI (Melnikov et al., 2016). The explanation pairs in TMPI can be aggregated to produce a real-valued convincingness score for each student’s submission.
However, aggregating these votes should be done with care: when a student chooses an explanation as convincing, they are doing so only with respect to the subset that were shown, as well as the one they wrote themselves. It has long been understood that obtaining pairwise preference data may be less prone to error on the part of the annotator, as it is a more straightforward task than rating on scales with more gradations. The trade-off, of course, is the quadratic scaling in the number of pairs one can generate. Pairwise preference is what we have in TMPI, since each student chooses one explanation as the most convincing only in relation to a subset of those that are shown. The potential permutations of explanations different students may see is intractably large for a typical question answered by 100+ students. A classical approach specifically proposed by Raman and Joachims (2014) for ordinal peer grading data is the Bradley-Terry (BT) model. The BT model (Bradley and Terry, 1952) for aggregating pairwise preference data into a ranked list assumes that predicting the winner of a pairwise “match-up” between any two items, is a function of the difference in the latent “strength” for those two items. These “strength” parameters can be calculated using maximum likelihood estimation. CrowdBT was originally proposed for evaluating relative reading level in pair passages (Chen et al., 2013). It is an extension of the BT method, which incorporates the quality of contributions of each annotator in a Crowdsourced setting.
In the specific context of evaluating argument convincingness from pairwise preference data, one of the first approaches proposed is based on constructing an “argument graph”. In this context, a weighted edge is drawn from node \(a\) to node \(b\) for every pair where argument \(a\) is labelled as more convincing than argument \(b\). After filtering passage pairs that lead to cycles in the graph, PageRank scores are derived from this directed acyclic graph, and then used as the gold-standard rank for convincingness (Habernal and Gurevych, 2016). This approach’s dataset is included in our study and labelled as UKP. A more straightforward heuristic, the WinRate score, has been recently shown to be a competitive alternative for the same dataset, wherein the rank score of an argument is simply the (normalized) number of times that argument is considered as more convincing in a pair, divided by the number of pairs it appears in (Potash et al., 2019). Yet another alternative, the Elo rating system, has been shown to successfully model student performance in intelligent tutoring systems (Pelánek, 2016). In this work, we will compare these aggregation methods on several datasets to evaluate their usefulness for measuring the convincingness of students’ explanations.
Our review would not be complete without covering Neural approaches that have become the
state-of-the-art in modelling argument convincingness. One such method is based on RankNet, joining
two Bidirectional Long-Short-Term Memory Networks in a Siamese architecture. By appending a
softmax layer to the output, pairwise preferences and overall ranks were jointly modelled in a dataset
made publicly available by the authors (Gleize et al., 2019). We refer to their dataset as
IBM_Evi in our study (see section 3.2 for details datasets). Most recently, a transfer-learning approach
has been proposed: using the architecture from a bidirectional encoder representations from
transformers, BERT(Devlin et al., 2018), which is pre-trained on masked language
modelling and next-sentence prediction, the model is fine-tuned for the task of predicting argument
convincingness. This approach has posted state-of-the-art results for pairwise preference data
as well on a large dataset predicting an absolute rank score (Gretz et al.,
2020).
The key difference between the above mentioned studies in modelling the quality rankings of arguments, and that of TMPI explanations, is that the students are not indifferent Crowdlabellers: each student will have just submitted their own explanation justifying their answer choice, and we analyze the aggregate of their choices as they indicate when a peer may have explained something better than themselves.
We leverage all of this related work in three ways:
- we use publicly available datasets of annotated pairwise preferences from the AM research community as a reference to evaluate our proposed methodology: UKP, IBM_ArgQ, and IBM_Evi. Section 3.2 provides further details on these datasets.
- we aggregate the pairwise preference data using methods that have been proposed in the context of learning systems: WinRate, BT, CrowdBT, and Elo. The mathematical formulation of each is described in more detail in section 4.1;
- we train a variety of regression models that are common to text mining in learning systems:
Linearregression,DecisionTrees,RandomForests, and different variants ofBERT(e.g.BERT_QandBERT_A) for regression described in section 4.3. Section 4.5 details how we evaluate the performance of these models.
3. Data
3.1. DALITE
The primary data source for this study is myDALITE.org, a hosted instance of an open-source project,
dalite1.
myDALITE.org is maintained by a Canadian researcher-practitioner partnership, SALTISE, focused
on supporting teachers in the development of active learning pedagogy. The platform is
primarily used for formative assessments, in “flipped-classroom” settings, where students
are assigned pre-instruction readings to be followed by relatively simple TMPI conceptual
questions.
One particular characteristic of TMPI data, which sets it apart from other comparative peer-review platforms, is best described when we consider the three options a student can take, described above in section 1: change to a different answer, change of explanation for same answer, or keep same answer and decide that their own explanation is best.
Moreover, when one of the answer choices is labelled as “correct” and the others are “incorrect”, as is often the case in question items from the STEM disciplines, we get one of four transitions: Right \(\rightarrow \) Right, Right \(\rightarrow \) Wrong, Wrong \(\rightarrow \) Right, or Wrong \(\rightarrow \) Wrong. In addition, transitions in which the answer choice remains the same (Right \(\rightarrow \) Right and Wrong \(\rightarrow \) Wrong) have two options as students select either their own or another student’s explanation as justification for their answer choice, giving a total of six transition types.
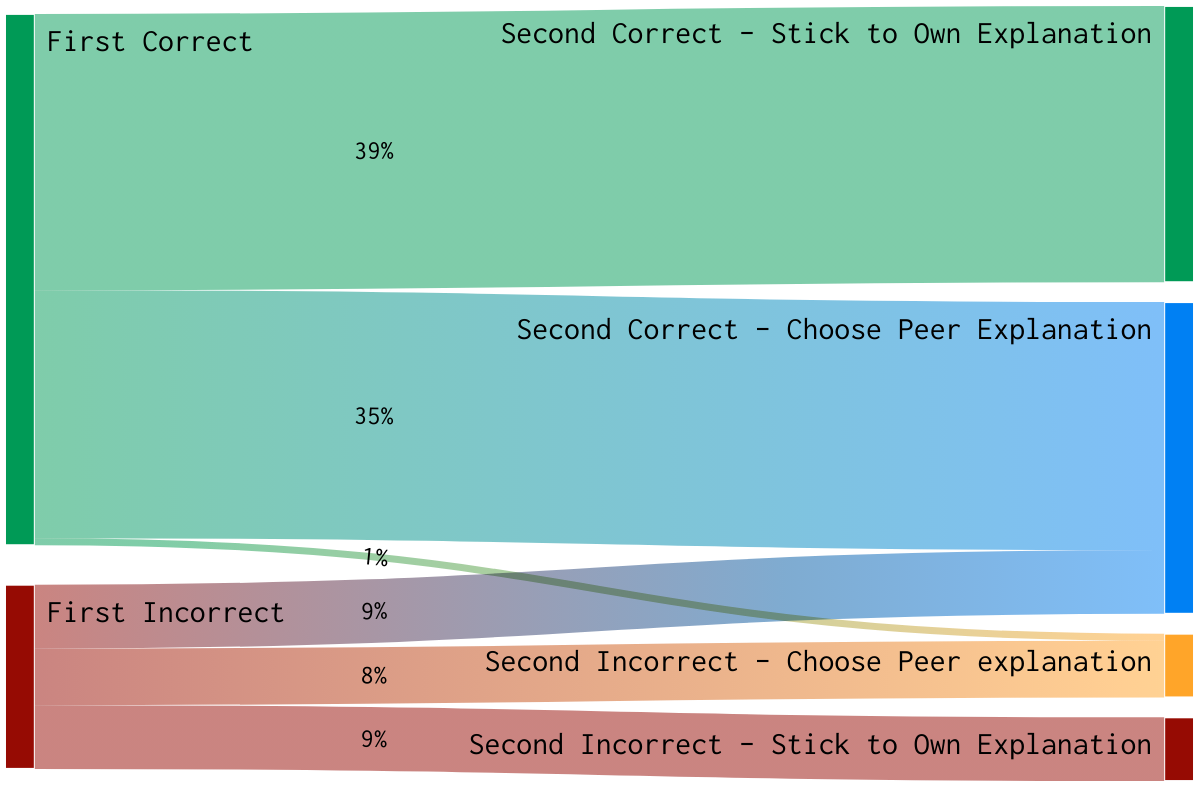
The transition possibilities and an example of the relative proportions present in the TMPI platform we study (Bhatnagar et al., 2020a), are shown in the Sankey diagram of figure 3.
Across all disciplines, we see two important trends: first, if a student chooses the correct answer on their first attempt and decides to keep that same correct choice on the review step, there is almost 50% chance that they chose a peer’s explanation as more convincing than their own. Second, if a student chooses an incorrect answer choice on their first attempt, there is a one in three chance that a peer’s explanation will convince them to change to the correct answer. These trends highlight the process of reflection students undertake in TMPI and the importance of leveraging student “vote” data to identify the best, most thought provoking content.
The data for this study comes from introductory level university science courses (Physics and Chemistry), and generally spans different teachers at several colleges and universities in Canada. The Ethics dataset comes from the 2013 run of a popular MOOC (Justice, offered by HarvardX). The TMPI prompts are slightly different from the Physics and Chemistry prompts, in that there is no “correct” answer choice, and that the goal is to have students choose a side of an argument, and justify their choice. Table 1 gives an overview of the datasets included in this study.
| topics | args | pairs | args/topic | pairs/topic | pairs/arg | wc | ||
|---|---|---|---|---|---|---|---|---|
| source | dataset | |||||||
| Arg Mining
| ||||||||
| IBM_ArgQ | 22 | 3474 | 9125 | 158 (144) | 415 ( 333) | 5 (1) | 24 ( 1) | |
| IBM_Evi | 41 | 1513 | 5274 | 37 ( 14) | 129 ( 69) | 7 (3) | 30 ( 3) | |
| UKP | 32 | 1052 | 11650 | 33 ( 3) | 364 ( 71) | 22 (3) | 49 (14) | |
| DALITE
| ||||||||
| Chemistry | 36 | 4778 | 38742 | 133 ( 29) | 1076 ( 313) | 7 (1) | 29 ( 6) | |
| Ethics | 28 | 20195 | 159379 | 721 (492) | 5692 (4962) | 7 (1) | 48 ( 8) | |
| Physics | 76 | 10840 | 96337 | 143 ( 42) | 1268 ( 517) | 7 (2) | 27 ( 5) | |
To stay consistent with terminology from argument mining research, we refer to a question-item as a “topic”. The transformation of TMPI student explanations (“args”) into “pairs” is described in section 4.
There are some critical filtering steps taken on raw data before we begin our analyses:
- Approximately 1 in 10 students decide that they prefer not to have their explanations shared with other students. These student answers are removed from the dataset.
- We exclude observations where students choose “I stick to my own rationale”. There is a strong bias toward this choice. We consider it may reflect a disengagement and the unwillingness to put effort into the task of evaluating all explanations. This filtering reduces our data by approximately 50%.
- Many question items have been completed by several hundreds of students. As such, almost half of all student explanations have been shown to another peer; thus we retain only those student answers that were presented to at least 5 other students (a threshold we chose based on a qualitative look at the distribution of how often each student explanation has been presented to a peer).
- As a platform for formative assessment, not all instructors provide credit for the explanations students write, and there are invariably some students who do not put much effort into writing good explanations. We include only those student answers that have at least 10 words.
- After the previous two steps, we only include data from those questions that have at least
100 remaining student answers (a threshold chosen based on minimum data required for
convergence of BT model in python implementation we use
choix). - We remove any duplicate pairs before the rank aggregation step that have the same “winning” label, as explanations that appear earlier on in the lifetime of a new question are bound to be shown more often to future students.
3.2. Argument Mining Datasets
Much of our methodology for the measure of convincingness is inspired by work on modelling argument quality, as described in section 2.3. To contextualize the performance of these methods in our educational setting, we apply the same methods to publicly available datasets from the AM research community as well and present the results. These datasets are described in table 1, alongside the TMPI data at the heart of our study. Each of these datasets was released not just with the labelled argument pairs, but holistic rank scores for each argument, which were each derived in different ways. We will be comparing our proposed measures of convincingness to these rank scores in section 4.5.
The UKP dataset (Habernal and Gurevych, 2016) is one of the first sets of labelled argument pairs to be released publicly. Crowdworkers were presented with pairs of arguments on the same stance of a debate prompt, and were asked to choose which was more convincing. In addition, each argument is assigned a real-valued quality score derived from the modified PageRank score described earlier.
The authors of the IBM_ArgQ dataset (Toledo et al., 2019) offer a similarly labelled dataset, but much more tightly curated, with strict controls on argument word count and relative length difference in each pair. This curation was partly in response to the observation that, across datasets, crowd labels could often be predicted simply by choosing the longer text from the pair. The authors also release in their dataset a real-valued convincingness score for each argument, which is the average of multiple binary relevance judgments provided by Crowdlabellers.
The labelled argument pairs in the IBM_Evi dataset (Gleize et al., 2019) are actually generated by scraping Wikipedia, and the crowd workers were asked to choose the argument from the pair that provided the more compelling evidence in support of the given debate stance.
We see in table 1 how the different disciplines in our TMPI dataset are comparable to the reference AM datasets (just proportionately larger).
4. Proposed methodology to model convincingness
We borrow our methodological approach from research in argument mining, specifically related to modelling quality along the dimension of convincingness. A common approach is to curate pairs of arguments made in defence of the same stance on the same topic. These pairs are then presented to Crowdworkers, whose task is to label which of the two is more convincing. The pairwise comparisons can then be combined using rank-aggregation methods to produce an overall ordered list of arguments. We extend this work to the domain of TMPI, and define prediction tasks that not only aim to validate this methodology, but help answer our specific research questions.2
4.1. Rank Aggregation
The raw data emerging from a TMPI platform is tabular in the form of student-item
observations. We refer to this raw format as Multiple-choice Explanation (MCE). As shown in
figure 4(a), the data fields in our MCE format include: the student’s first answer choice, their
accompanying explanation, the peer explanations shown on the review step (as in figure 1b), the
student’s second answer choice, and finally, the peer explanation they chose as most convincing
(None if they choose to “stick to their own”). Timestamps for these events are associated as
well.
The process starts by filtering the data in MCE format (described in section 3.1) to obtain the figure 4(a) table. This data is processed into explanation pairs 4(b), which is later transformed into pointwise convincingness scores 4(c). When a student chooses an explanation (other than theirs), pairs are created for all explanations that were shown as alternatives, including the student’s original explanation. In figure 4’s example, the choice of e\(_{25}\) out of the eight peer explanations thus results in seven pairs, plus one that includes the student’s own.
We apply the following rank aggregation techniques order to derive a real-valued convincingness rank score for each student explanation, as depicted in figure 4(c).
- 1.
- WinRate: as described in Potash et al. (2019), this measure of argument quality is defined as the number of times it is chosen as more convincing in a pairwise comparison, normalized by the number of pairs in which it appears. In the context of TMPI, when we calculate the WinRate of a student explanation after the data transformation depicted in figure 4a and figure 4b, we take a step toward including the effect of comparative judgment, as pairs are specifically constructed for each observation from the explanation that was chosen, and the ones that were shown.
- 2.
- BT score, which is the argument “quality” parameter estimated for each explanation,
according to the Bradley-Terry model, where the probability of argument \(a\) being chosen
over argument \(b\) is given by:
\[ P(a>b) = \frac {1}{1+e^{\beta _b-\beta _a}} \] where \(\beta _i\) is the latent strength parameter of argument \(i\).
We decompose each student-item observation into argument pairs, where the chosen explanation is paired with each of the other shown ones, and the pair is labelled with \(-/+1\), depending on whether the chosen explanation is first/second in the pair. Assuming there are \(K\) students, and \(S_k\) pairs labelled by the \(k^{th}\) student, the latent strength parameters are estimated by maximizing the log-likelihood given by: \[ \ell (\boldsymbol {\beta })=\sum _{K}\sum _{(i,j)\epsilon S_k}^{} \log \frac {1}{1+e^{\beta _i - \beta _j}} \] subject to \(\sum _{i}\beta _i=0\).3
- 3.
- The Elo rating system (Elo, 1978), which was originally proposed for ranking chess
players, has been successfully used in adaptive learning environments (see Pelánek 2016
for a review). This rating method can be seen as a heuristic re-parametrization of the BT
method above, where the probability of argument \(a\) being chosen over argument \(b\) is given
by
\[ P(a>b) = P_{ab} = \frac {1}{1+10^{(\beta _b-\beta _a)/\delta }} \]
where \(\delta \) is a scaling constant. All arguments are initialized with an initial strength of \(\beta _0\), and
the rating of any argument is only updated after it appears in a pairwise comparison with
another. The rating update rule transfers latent “strength” rating points from the loser, to
the winner, in proportion to the difference in strength:
\[ \beta _a':=\beta _a+K(P_{ab} - \beta _a) \] where \(K\) is a factor that can be adjusted to make the score more or less sensitive to recent data. It is set to 24 in the current experiments.
While the BT model can be thought of as consensus approach (all rank scores are re-calculated after each pair is seen), Elo ratings are dynamic and implicitly give more weight to recent data (Aldous, 2017).
- 4.
- CrowdBT (Chen et al., 2013) is an extension of the BT model, tailored to
settings where different annotators may have assigned opposite labels to the same pairs
and the reliability of each annotator may vary significantly. A reliability parameter \(\eta _k\) is
estimated for each student, where the probability that student \(k\) chooses argument \(a\) as more
convincing than \(b\) is given by
\[ \eta _k \equiv P(a >_k b | a >b ) \]
where \(\eta _k \approx 1\) if the student \(k\) agrees with most other students, and \(\eta _k \approx 0\) if the student is in opposition to their peers. This changes the model of argument \(a\) being chosen over \(b\) by student \(k\) to \[ P(a >_k b) = \eta _k \frac {e^{\beta _a}}{e^{\beta _a}+e^{\beta _b}} + (1-\eta _k) \frac {e^{\beta _b}}{e^{\beta _a}+e^{\beta _b}} \] and the log-likelihood maximized for estimation to
\[ \ell (\boldsymbol {\eta },\boldsymbol {\beta })=\sum _{K}\sum _{(i,j)\epsilon S_K}^{} \log \left [ \eta _k \frac {e^{\beta _a}}{e^{\beta _a}+e^{\beta _b}} + (1-\eta _k) \frac {e^{\beta _b}}{e^{\beta _a}+e^{\beta _b}} \right ] \]
This method is currently used in the comparative evaluation platform JuxtaPeer (Cambre et al., 2018).4
Section 4.5 describes how we evaluate the fit of these rank aggregation methods to our data.
4.2. Linguistic Features
Once the pairwise votes are converted to global ranking scores of convincingness, we next build on these results to predict these rankings for each explanation, using different representations of the text in those explanations. We cast RQ2, the goal of identifying the linguistic features behind convincingness, as a regression task, predicting the argument convincingness scores via a feature-rich document vector.
The list of features included here is derived from related work in argument mining (Habernal and Gurevych, 2016, Persing and Ng, 2016), on student essays and automatic short answer scoring (Mohler and Mihalcea, 2009).
- Lexical & statistical features: These include uni-grams, type-token ratio and number of keywords (defined by open-source discipline-specific textbook). These features may capture lexical diversity and discipline specific keywords that are predictive of convincingness. Moreover, a statistical feature we propose to include is the number of equations (captured by a regular expression) used by a student in their explanation, as they appear very often in the TMPI platform data. In STEM disciplines, many students choose to reference their knowledge around a body of formulae to justify their reasoning.
- Syntactic features: We surmise that such features are question and discipline agnostic and that there are patterns used by students that are simpler to understand for their peers. These include part-of-speech (POS) tags (e.g. noun, preposition, verb, etc.), and POS bi-grams and tri-grams as well. We replace each word in the student explanation with its universal POS tag and derive features from the normalized counts of each of these tags for each student explanation5. We also include counts of certain more detailed Modal verbs (e.g. must, should, can, might), and the average height of syntactic parse trees for each sentence.
-
Semantic features: we build from work in automatic short answer grading, which often employs vector space models: student answers are represented as embeddings, and their quality is evaluated based on vector similarity/distance with the embeddings of expert, correct text. We make our choice of different embedding spaces based on increasing levels of specificity:
- Generally available pre-trained GloVe vectors (Pennington et al.,
2014) have been used for short-answer grading (Magooda et al.,
2016, Riordan et al., 2017). Using the 300-dimensional vectors, we
calculate similarity metrics to i) all other explanations (following results from
Gagnon et al. (2019)), ii) the question item text, and, when available,
iii) a teacher provided “expert” explanation (feature is
NAotherwise). - We derive our own discipline-specific embedding vectors, trained on corresponding
open-source textbooks6.
We experiment with a word-based vector space model, Latent Semantic Indexing
(
LSI) (Deerwester et al., 1990), due to its prevalence in text analytics in educational data mining literature, as well asDoc2Vec(Le and Mikolov, 2014), which directly models the compositionality of all the words in a sentence7. We take the text of the question prompt and, when available, an “expert explanation” provided by teachers for each question, and determine the 10 most relevant sub-sections of the textbook. We then calculate the minimum, maximum, and mean cosine similarity for each student explanation over these 10 discipline-specific “reference texts”.
These semantic features are meant to leverage the discipline-specific linguistic knowledge contained in reference textbooks.
- Generally available pre-trained GloVe vectors (Pennington et al.,
2014) have been used for short-answer grading (Magooda et al.,
2016, Riordan et al., 2017). Using the 300-dimensional vectors, we
calculate similarity metrics to i) all other explanations (following results from
Gagnon et al. (2019)), ii) the question item text, and, when available,
iii) a teacher provided “expert” explanation (feature is
- Readability features include empirically derived formulas which have been shown to predict how difficult it is to read a text, and which have been used extensively in automatic essay scoring research (Graesser et al., 2004). The most common indices are the ones we adopt, including Flesch-Kincaid reading ease and grade level, Coleman-Liau automated readability index, and a normalized number of spelling errors8.
Features typical to NLP analyses in the context of writing analytics not included here are sentence-to-sentence cohesion, sentiment, and psycho-linguistic features, as we deem them not pertinent for shorter responses that deal with STEM disciplines.
In our effort to address RQ2, these high dimensional feature-rich representations are passed through
a uni-variate feature selection step, wherein all features are ordered in decreasing order of variance, and
the top 768 features are retained, to be used as input for the classical regression models described
earlier. We chose this vector representation size to match the size of the contextual embeddings in the
neural BERT models, described in section 4.3, and compare their performance in a fair manner. These
neural models do not provide the same transparency for interpretation upon inspection, but leverage
pre-training on massive corpora to bring a broad linguistic understanding to our regression
task.
4.3. Regression Models
The machine learning convincingness models we frame as a regression task are inspired from
writing analytics literature, as well as the design objective of maximizing interpretability: the ability
to inspect models to explain predictions of which student answers are most convincing is
paramount in providing pedagogical support to students and teachers. The models we include in
this study are Linear regression, Decision Tree regression, and Random Forest
regressors.
As demonstrated in related work (Habernal and Gurevych, 2016), argument Length is a
challenging baseline to beat when modelling convincingness in pairwise preference data. While
Length is not in itself a linguistic nor a semantic feature, it is likely that the greater the amount of
words, the greater is the opportunity to construct a convincing argument. It may also well be a
confounding factor that correlates with engagement and, in turn, with convincingness. Whatever the
reason is for its effectiveness, we set explanation Length (the number of white-space separated
tokens) as our regression baseline.
All features described in section 4.2 are used in the regression models described above.
4.4. BERT transformer model
Transformer models are at the basis of the most recent approaches for the prediction of argument
convincingness scores (Gretz et al., 2020, Fromm et al., 2023, Thorburn
and Kruger, 2022, Falk and Lapesa, 2023, for example). We also fine-tune a pre-trained bi-directional
neural transformer model, BERT, with argument mining reference data sets, as well as the TMPI data
from our three disciplines. In line with the best-performing model in Gretz et al. (2020),
we go beyond this and train a different model where the input is augmented with the question
prompt. The text of the question, along with any text from an accompanying image caption, is
combined with the student explanation, separated by the model-specific [SEP] token, and
input as a pair of sequences during fine-tuning and inference (henceforth referred to as
BERT_Q)).
Finally, in the Physics and Chemistry datasets from our TMPI platform, many of the questions are
accompanied by an expert explanation, written by the teacher-author of the question (the purpose of
which is to provide some feedback to the student to read after they have submitted their second answer
choice in the review step). We fine-tune a variation of BERT_Q and combine expert-written text,
separated by the SEP token, with the student explanation, and serve as input to the transformer (instead
of the topic prompt). We refer to this approach as BERT_A. The theoretical grounding for the use of
these models in the study of convincingness stems from the large gain of performance of these models
in several natural language processing tasks. BERT-like models and pre-trained language
models have revolutionized natural language processing tasks with the ability to transfer
knowledge from pre-training phases and the task of convincingness makes no exception in this
regard.
In each of BERT, BERT_Q and BERT_A, the contextual embedding of the model-specific [CLS]
token in the last layer of the fine-tuned transformer is fed as input into a fully dense regression layer
that outputs a predicted convincingness score.
4.5. Evaluation of the proposed methodology
In order to address research question RQ1 and evaluate the choice of rank aggregation methods, we perform two experiments. First, we need to ascertain that we can derive a valid measure of convincingness given a set of pairwise comparisons of explanations. This is accomplished by comparing the calculated score with an independent external score obtained from human judgements (external validity experiment), and by measuring how the calculated score can reliably predict back the pairwise order in a cross-validation scheme (internal validity experiment).
Finally, we address RQ2 by comparing a range of models that use the convincingness score as the ground truth for training. Each model varies in how it uses linguistic features to predict convincingness.
4.5.1. External validity of the convincingness score
We begin by measuring the correlation between the scores output from the rank aggregation methods described in section 4.1, and the “reference” scores provided with the AM datasets obtained from Crowdlabellers (outlined in section 3.2). For each topic in the different AM datasets, we calculate the Pearson correlation between the “reference” scores of each argument, and WinRate, BT, Elo scores aggregated from the pairwise preference data. (We cannot include CrowdBT here, as the AM datasets do not include information on which crowd workers labelled which argument pairs, which is a requirement for estimating the annotator-specific \(\eta _k\)). The distribution of Pearson correlation coefficients across the different topics for each dataset is shown in the box plots in figure 5.
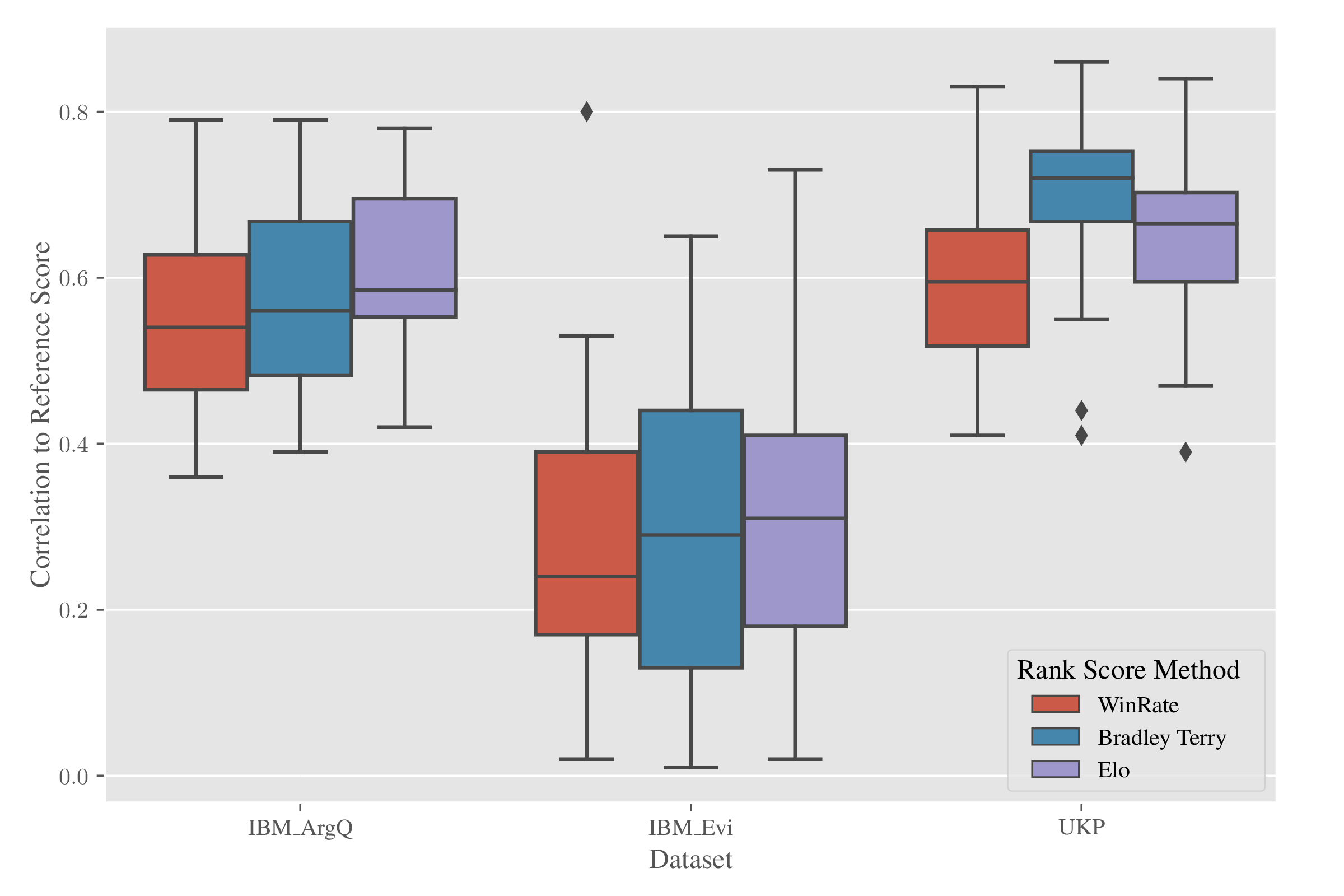
While the variance across topics of the correlation coefficients between the “out-of-the-box” reference scores and our rank-aggregation scores can be quite large, the median lies between 0.5 and 0.7 for the UKP and IBM_ArgQ datasets. The relative alignment between our choice of rank aggregation techniques (WinRate, Bradley-Terry, and Elo), and the modified PageRank score provided with UKP, indicates that all capture approximately the same information about overall convincingness. Also of note is the relatively high correlation between the IBM_ArgQ reference rank score and the aggregation methods we include in our study. The IBM_ArgQ reference convincingness score was actively collected by the authors of the dataset: first, they presented crowd workers with individual arguments, and prompted them to give a binary score of 1/0, based on whether “they found the passage suitable for use in a debate”. The real-valued score for each argument is simply the average of the score over all labellers. The correlation between WinRate, Bradley-Terry, and Elo, and this actively collected reference score, would indicate that these methods capture a ranking that is more than just an artifact of a computational model.
4.5.2. Internal validity of the convincingness score
In order to evaluate a measure of reliability of aggregated convincingness scores, we employ a validation scheme similar to the one proposed by Jones and Wheadon (2015). Students are randomly split into two batches, and their answers are used to derive two independent sets of convincingness scores, as shown in figure 6.
We apply this reliability estimate on the derived rank scores from the pairwise preference data
from dalite (we cannot perform this evaluation on the reference AM datasets, as we
do not know who provided each pairwise preference label). Finally, we dis-aggregate the
results by possible TMPI transition types in figure 7, in order to inspect if there are any
systematic differences between the cases when students are casting a vote for an explanation
for a different answer choice than their own, or whether their initial guess was correct, or
not.
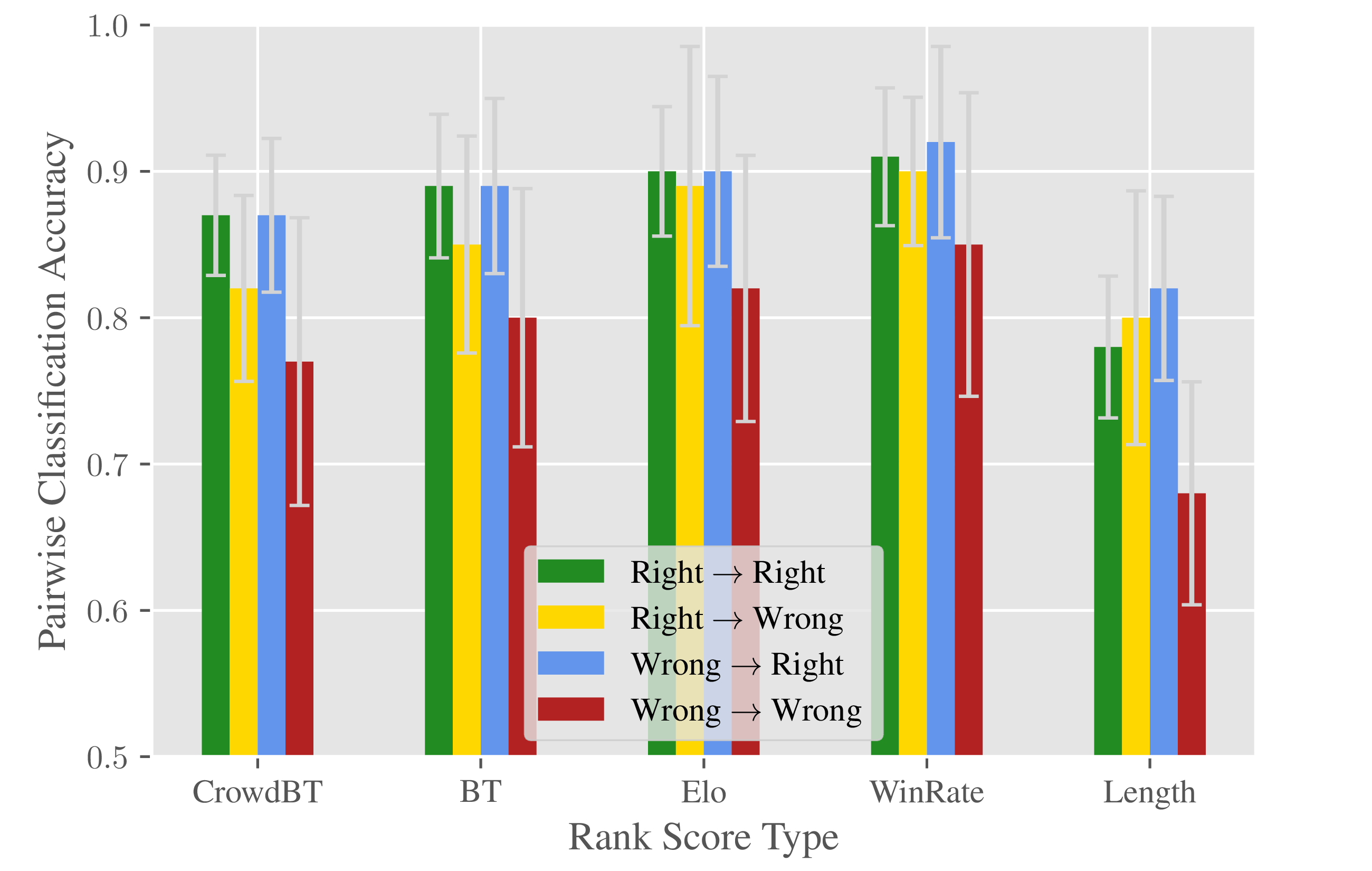
Note that, as shown in the relative proportions of the Sankey diagram (figure 3, the vast majority of the data is represented in the Right\(\rightarrow \)Right transition (the rarest transition is Right\(\rightarrow \)Wrong). When we consider using the rankings derived from one batch of students and use them to predict the pairwise preferences of the other batch, the classification accuracies are roughly equivalent across the different rank score methods (figure 7). Ideally, we could compare these results with an inter-judge agreement which would provide an estimate of the maximum results we could expect. This is left for future work.
At the other end of the performance spectrum, we use the baseline “Length” method, where the
pairwise preference is determined by simply choosing the explanation with the most words. All
methods outperform this baseline.
4.5.3. Predicting convincingness
We have so far addressed RQ1 and determined that WinRate, Elo and BT are valid and reliable rank-aggregation scores that outperform the simple, yet relatively accurate, length indicator. We now turn to the second step of our proposed methodology which addresses research question RQ2 (identify the most salient linguistic features of convincingness), and builds feature-rich supervised regression models to predict the individual argument scores.
We choose our feature sets based on relevant related research, as described in section 4.2, and use Pearson correlation9 coefficients to measure performance, as is standard practice in the literature on point-wise prediction of argument quality along the dimension of convincingness.
In order to estimate the generalizability of these models to new question items, we employ a “cross-topic” cross-validation scheme, wherein we hold out all of the answers on one question item as the test set, training models on all of the answers for all other question items in the same discipline. This approach is meant to capture discipline-specific linguistic patterns, while addressing the “cold-start” problem for new items before vote data can be collected.
Once feature-rich models are trained and tested under this validation scheme, we inspect these using permutation importance (Fisher et al., 2019), a model agnostic feature importance version originally introduced by Breiman (2001) random forests. Each feature is randomly permuted for a set number of repetitions (we choose the default \(n_{\mathrm {repeats}}=30\)). This permutation has the effect of eliminating its potential predictive contribution and is akin to an ablation study. The importance of that feature is measured by the average decrease in performance of the model on the non-perturbed dataset10.
We devote the next section to the results of this experiment as they are more central to the main contribution of this paper.
5. Predicting convincingness, results and discussion
Given an absolute score of convincingness from pairwise rankings, the next and main contribution of this study is to propose models of learnersourced explanation quality labels inside TMPI learning environments. A total of seven models are compared and described in section 4.3. The first four use the linguistic features described in section 4.2, whereas the BERT models use raw text:
- Length
- : number of words in explanation.
- Linear
- : a linear regression.
- DTree
- : decision tree.
- RF
- : random forest.
- BERT
- : BERT transformer with explanation text.
- BERT_Q
- : BERT transformer with explanation and question texts.
- BERT_A
- : BERT transformer with explanation, question, and expert answers texts.
5.1. Results — Argument Mining Datasets
We begin by applying this methodology to publicly available AM datasets in table 2. We train our different models to predict the real-valued convincingness score provided by these datasets.
| Dataset | Method | Length | Linear | DTree | RF | BERT | BERT_Q | Average |
|---|---|---|---|---|---|---|---|---|
| IBM_ArgQ | BT | 0.16 | 0.18 | 0.21 | 0.31 | 0.55 | 0.55 | 0.33 |
| WinRate | 0.13 | 0.23 | 0.21 | 0.28 | 0.52 | 0.51 | 0.31 | |
| reference | 0.14 | 0.14 | 0.17 | 0.25 | 0.37 | 0.39 | 0.33 | |
| average | 0.15 | 0.18 | 0.20 | 0.28 | 0.48 | 0.48 | 0.32 | |
| IBM_Evi | BT | 0.11 | 0.20 | 0.30 | 0.50 | 0.52 | 0.33 | |
| WinRate | 0.13 | 0.17 | 0.21 | 0.30 | 0.46 | 0.48 | 0.29 | |
| reference | 0.15 | 0.28 | 0.25 | 0.33 | 0.50 | 0.56 | 0.34 | |
| average | 0.13 | 0.22 | 0.21* | 0.31 | 0.49 | 0.52 | 0.32 | |
| UKP | BT | 0.54 | 0.20 | 0.42 | 0.58 | 0.60 | 0.64 | 0.50 |
| WinRate | 0.58 | 0.18 | 0.46 | 0.60 | 0.71 | 0.72 | 0.54 | |
| reference | 0.33 | 0.23 | 0.34 | 0.23 | 0.26 | 0.28 | ||
| average | 0.48 | 0.20 | 0.42* | 0.51 | 0.51 | 0.54 | 0.44 | |
| * Average after imputation for missing values
| ||||||||
It should be noted that the real-valued reference scores that are provided with the argument mining datasets, and are the target variables for the model training in table 2, are each calculated in different ways. For example, in the UKP dataset, the ground truth convincingness score provided for each argument by the authors, is derived by constructing an argument graph, and calculating a variant of the PageRank score, after removing cycles induced by the pairwise data (e.g. cases where A is more convincing than B, B is more convincing than C, but C is more convincing than A). For IBM_ArgQ, the real-valued score is the mean of multiple binary “relevance judgments” explicitly collected by the authors from a set of Crowd-labellers. Finally, the real-valued score accompanying arguments in IBM_Evi is the output of a regression layer that is appended to a two-armed Siamese Bi-LSTM model, wherein only one arm is provided with the GloVe embedding of the input argument.
To allow a consistent comparison across datasets and across methods in table 2, we train our models to predict a target variable that can be calculated from any pairwise preference dataset, namely WinRate or BT. To the best of our knowledge, we are the first to propose, evaluate, and subsequently model a common set of rank aggregation methods for the calculation of point-wise argument quality scores from pairwise preference data.
While our best-performing feature-rich model (Random Forests) beats the Length baseline,
the fine-tuned neural transformer models BERT and BERT_Q systematically outperform all other
methods. This pattern holds across the three reference datasets, when all trained for the same task,
under the same cross-topic validation scheme, in line with similar results from the literature described
in section 2. Given the superiority of pre-trained language models and their impact on raising
performance in several natural language processing tasks, these results are not surprising, but come at
the expense of the results’ explainability for such black-box models, a research avenue that is left for
future work.
Training our regressors to learn the WinRate and Bradley-Terry scores yields better correlations than when we try to predict the reference scores accompanying the datasets (table 2). Beyond the added benefit of WinRate and Bradley-Terry being universal measures across data sets, the higher correlation values for WinRate and BT indicate that they are better aligned with the linguistic features used to measure convincingness.
5.2. Results - TMPI discipline-specific datasets
We apply this same methodology to our three TMPI discipline-specific datasets in table 3, and
observe that BERT_Q is also the best performing model.
The success of the neural approach over feature-rich regressors raises a barrier to our objective of
identifying the linguistic properties of what students find convincing in their peers’ explanations.
However, it should be noted that Length baseline is also very effective for Physics and Chemistry,
and that BERT may be getting much of its information from the number of empty tokens required when
padding the different inputs to equal length. The feature-rich Random Forest model
achieves almost the same performance without access to the informative feature of explanation
length.
Nonetheless, for the Physics and Chemistry disciplines, no models significantly outperform the
Length baseline, which seems to indicate that more work is needed in determining the features of
those longer explanations that they find most convincing. This is true also when our rank aggregated
score jointly estimates the student’s agreement with their peers, as in the CrowdBT score (results in
table 3).
The gain in performance over the Length baseline is most pronounced for Ethics. This may be
best explained by the inherent similarities between the Ethics TMPI data, and the argument
mining datasets: the topic prompts are subjective and personal, and the available answer
options students must choose from are also limited: typically, the options are two opposing
stances of an argument, as can be seen in the sample data in Appendix A’s tables 4 and
5.
Finally, augmenting the input of BERT to incorporate the question prompt, in BERT_Q, yields
virtually no improvement. This pattern also holds true for the argument mining datasets. This may
indicate that, unlike the potential correctness of an explanation, its convincingness may be independent
of the question prompt.
The slight decrease in performance of BERT_A might reflect that explanations written by content
experts are different from student explanations, and do not help model convincingness as judged by
peers. But considering the small difference, this remains speculative.
| Dataset | Method | Length | Linear | DTree | RF | BERT | BERT_Q | BERT_A | Average |
|---|---|---|---|---|---|---|---|---|---|
| Chemistry
| |||||||||
| BT | 0.36 | 0.21 | 0.26 | 0.35 | 0.37 | 0.37 | 0.36 | 0.33 | |
| CrowdBT | 0.36 | 0.20 | 0.27 | 0.35 | 0.36 | 0.37 | 0.35 | 0.32 | |
| WinRate | 0.32 | 0.14 | 0.25 | 0.31 | 0.34 | 0.34 | 0.33 | 0.29 | |
| average | 0.31 | 0.16 | 0.22 | 0.28 | 0.32 | 0.32 | 0.30 | 0.28 | |
| Physics
| |||||||||
| BT | 0.37 | 0.27 | 0.31 | 0.35 | 0.40 | 0.40 | 0.38 | 0.35 | |
| CrowdBT | 0.38 | 0.25 | 0.30 | 0.37 | 0.41 | 0.41 | 0.39 | 0.36 | |
| WinRate | 0.36 | 0.19 | 0.27 | 0.35 | 0.38 | 0.39 | 0.37 | 0.35 | |
| average | 0.33 | 0.20 | 0.26 | 0.32 | 0.36 | 0.36 | 0.34 | 0.31 | |
| Ethics
| |||||||||
| BT | 0.17 | 0.21 | 0.21 | 0.25 | 0.32 | 0.31 | 0.24 | ||
| CrowdBT | 0.17 | 0.19 | 0.24 | 0.28 | 0.32 | 0.32 | 0.25 | ||
| WinRate | 0.16 | 0.17 | 0.22 | 0.26 | 0.29 | 0.29 | 0.23 | ||
| average | 0.16 | 0.16 | 0.20 | 0.24 | 0.28 | 0.28 | 0.22 | ||
It should be noted that under our cross-topic validation scheme, different question-level folds witness significantly better agreement between model predictions and rank aggregated convincingness scores.
In both Physics and Chemistry, the question-level folds where our models performed worst were with question prompts that ask students to choose one true statement from among a selection (e.g. Which of the following statements about the force of gravity is false? a) ..., b) ...,). We posit that the language students use to formulate their explanations in such a multiple-choice question item, many describing their internal process of elimination to find the correct answer choice, include patterns our models are not able to learn in the training data.
Our contributions are centred on our research questions stated at the beginning of this study. In terms of RQ1, we present a methodology grounded in argument mining research and empirically demonstrate its validity in the context of TMPI. We present the result of different approaches to rank aggregation from pairwise preference data so as to calculate a convincingness score for each student explanation. The pairwise transformation of TMPI data, into a format similar to research from argument research (as described in figure 4) allows for a comparison to related work. The results, when we train our models to predict the raw WinRate, are significantly worse (table 3) than any of the other rank aggregation methods. This confirms the findings of Potash et al. (2019), who first proposed the pairwise WinRate heuristic as a more reliable regression target. (While the Elo rank aggregation score is much faster than BT, our modelling results were by far worse than the alternatives described in the tables here.) With such simple methods as WinRate and the Bradley-Terry scores to measure and rank student explanations in a TMPI environment, instructor reports can focus attention on where students may have gaps in their knowledge, based on their reading/evaluating of their peers’ explanations.
5.3. Model inspection for important linguistic features
In an effort to provide insight into the feature-rich regression models for predicting argument convincingness (RQ2), we look at our best-performing folds of our regression task, and note the features with the highest permutation importance (from highest to lowest):
- Type Token Ratio
- Dale-Chall Readability score
- Number Equations
- Vector Similarity to others (GloVe)
- Vector Similiarity to related textbook portions using LSI
- Number of spelling errors
- Flesch Kincaid reading ease score
- Mathematical expressions used as a noun subject for a verb e.g. “\(F=ma\), tells us that ...”
Another approach we explore to determine which linguistic features are most associated with
explanations that are deemed convincing by students, is taking our best performing neural transformer
model, BERT_Q, and finding the features most correlated with its predicted rankings. We find that the
same features which are listed above are also those most highly correlated with the predicted
convincingness score.
It is these types of features that can provide pedagogical insight to instructors when parsing through data generated inside TMPI based activities. These features are predictive of what the students find most convincing in their peers’ explanations, and hence offer a much needed lens into how students operate when at the upper levels of Bloom’s taxonomy (Bloom et al., 1956), evaluating each others’ words in a comparative setting.
6. Limitations and Future Work
In the current study, we focused on a measure of the propensity of students to choose an explanation, which we called convincingness, as a proxy for explanation quality. Ultimately, we hope convincingness can be used as a feature that could guide teachers and TMPI designers towards determining an explanation set shown to students that can maximise learning gains (section 1.1). But convincingness is only a feature that may help lead to this ultimate goal.
In fact, convincingness in TMPI should not be confounded with convincingness in the argument mining field. In a traditional crowdsourcing setting, the people who choose the most convincing explanations are not also the ones who wrote them. In TMPI, the student will not only be comparing their peers’ explanations with each other, but also against the explanation they just submitted. The effect of this can be seen in the 50% chance that students decide to “stick to their own” explanation in myDALITE.org. On the one hand, students who are disengaged and do not wish to invest in the effort of analyzing each explanation’s quality will stick to their own choice. On the other hand, the “vote” a student casts for a peer’s explanation might not be due to its relative convincingness, but instead a reflection of how confident that student is in their own answer choice, and even their own understanding of the underlying concept. While these factors may not bias the pairwise choice of explanations, it warrants the exclusion of “stick to their own” choice for TMPI data. It also sheds evidence as to why the measure convincingness in argument mining is different from the TMPI context.
Other directions for future work include improving the performance of feature-rich models by
incorporating “argument structure” features, which require the identification of claims and premises as
a feature engineering step. The combination of such argument-features with a neural model has been
shown to be effective in the grading of persuasive essays (Nguyen and Litman, 2018). We also note that
valuable insights could be gained through ablation studies and more in depth analysis of the results
to better understand what features are most important and why one model works better
than another. For instance, we hypothesized that BERT models might be able to boost their
performance by simply including the length feature, a strong predictor in some domains. In
fact, a number of conjectures were made in the analysis of the results that warrant further
investigations.
Another important step to take is to confirm whether simply showing students convincing explanations can improve learning or drive engagement. A previous study has shown that how instructors integrate TMPI with their in-class instruction has an impact on learning gains across the semester (Bhatnagar et al., 2015).
Finally, our work can inform pedagogical practice in how teachers design conceptual questions meant to promote the elaboration of rich self-explanations, which in turn can lead to deep reflection among peers in TMPI. Recent research on identifying the types of question-items best suited for in-class PI encourages the use of non-numerical prompts in order to foster rich discussion (Cline et al., 2021). One metric the authors propose for evaluating the quality of a question is the variability of votes around the different answer choices. More work is needed in order to extend this notion to TMPI, where a formal measure of question quality can help instructors pose more thought-provoking tasks for their students.
Acknowledgements
Funding for the development of myDALITE.org is made possible by Entente-Canada-Quebec, and the Ministère de l’Éducation et Enseignment Supérieure du Québec. Funding for this research was made possible by the support of the Canadian Social Sciences and Humanities Research Council Insight Grant. This project would not have been possible without the SALTISE/S4 network of researcher practitioners, and the students using myDALITE.org who consented to share their learning traces with the research community.
Editorial Statement
Michel Desmarais and Amel Zouaq were not involved with the journal’s handling of this article to avoid a conflict with their role as Editorial Team Members. The entire review process was managed by Andrew M. Olney, Associate Editor.
References
- Aldous, D. 2017. Elo ratings and the sports model: A neglected topic in applied probability? Statistical science 32, 4, 616–629.
- Bentahar, J., Moulin, B., and Bélanger, M. 2010. A taxonomy of argumentation models used for knowledge representation. Artificial Intelligence Review 33, 3, 211–259.
- Bhatnagar, S., Desmarais, M., Whittaker, C., Lasry, N., Dugdale, M., and Charles, E. S. 2015. An analysis of peer-submitted and peer-reviewed answer rationales, in an asynchronous Peer Instruction based learning environment. In Proceedings of the 8th International Conference on Educational Data Mining, O. C. Santos, J. G. Boticario, C. Romero, M. Pechenizkiy, A. Merceron, P. Mitros, J. M. Luna, C. Mihaescu, P. Moreno, A. Hershkovitz, S. Ventura, and M. Desmarais, Eds. International Educational Data Mining Society, Madrid, Spain, 456–459.
- Bhatnagar, S., Zouaq, A., Desmarais, M., and Charles, E. 2020a. A Dataset of Learnersourced Explanations from an Online Peer Instruction Environment. In International Conference on Educational Data Mining (EDM) (13th, Online, Jul 10-13, 2020), A. N. Rafferty, J. Whitehill, C. Romero, and V. Cavalli-Sforza, Eds. International Educational Data Mining Society, 350–355.
- Bhatnagar, S., Zouaq, A., Desmarais, M. C., and Charles, E. 2020b. Learnersourcing Quality Assessment of Explanations for Peer Instruction. In Addressing Global Challenges and Quality Education, C. Alario-Hoyos, M. J. Rodríguez-Triana, M. Scheffel, I. Arnedillo-Sánchez, and S. M. Dennerlein, Eds. Springer International Publishing, Cham, 144–157.
- Bloom, B. S., Engelhart, M. D., Furst, E., Hill, W. H., and Krathwohl, D. R. 1956. Handbook I: Cognitive Domain. David McKay, New York.
- Bradley, R. A. and Terry, M. E. 1952. Rank analysis of incomplete block designs: I. The method of paired comparisons. Biometrika 39, 3/4, 324–345.
- Breiman, L. 2001. Random forests. Machine learning 45, 1, 5–32.
- Burrows, S., Gurevych, I., and Stein, B. 2015. The eras and trends of automatic short answer grading. International Journal of Artificial Intelligence in Education 25, 1, 60–117.
- Cambre, J., Klemmer, S., and Kulkarni, C. 2018. Juxtapeer: Comparative Peer Review Yields Higher Quality Feedback and Promotes Deeper Reflection. In Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems - CHI ’18. ACM Press, Montreal QC, Canada, 1–13.
- Charles, E. S., Lasry, N., Bhatnagar, S., Adams, R., Lenton, K., Brouillette, Y., Dugdale, M., Whittaker, C., and Jackson, P. 2019. Harnessing peer instruction in- and out- of class with myDALITE. In Fifteenth Conference on Education and Training in Optics and Photonics: ETOP 2019. Optical Society of America, Quebec City, Canada, 11143_89.
- Charles, E. S., Lasry, N., Whittaker, C., Dugdale, M., Lenton, K., Bhatnagar, S., and Guillemette, J. 2015. Beyond and Within Classroom Walls: Designing Principled Pedagogical Tools for Student and Faculty Uptake. In Exploring the Material Conditions of Learning: The Computer Supported Collaborative Learning (CSCL) Conference 2015, Volume 1, O. Lindwall, P. Hakkinen, T. Koschman, P. Tchounikine, and S. Ludvigsen, Eds. International Society of the Learning Sciences, Inc.[ISLS].
- Chen, X., Bennett, P. N., Collins-Thompson, K., and Horvitz, E. 2013. Pairwise ranking aggregation in a crowdsourced setting. In Proceedings of the sixth ACM international conference on Web search and data mining. Association for Computing Machinery, New York, New York, 193–202.
- Chi, M. T., Leeuw, N., Chiu, M.-H., and LaVancher, C. 1994. Eliciting self-explanations improves understanding. Cognitive science 18, 3, 439–477.
- Cline, K., Huckaby, D. A., and Zullo, H. 2021. Identifying Clicker Questions that Provoke Rich Discussions in Introductory Statistics. PRIMUS 0, ja, 1–32.
- Crouch, C. H. and Mazur, E. 2001. Peer instruction: Ten years of experience and results. American Journal of Physics 69, 9, 970–977.
- Deerwester, S. C., Dumais, S. T., Landauer, T. K., Furnas, G. W., and Harshman, R. A. 1990. Indexing by latent semantic analysis. JASIS 41, 6, 391–407.
- Denny, P., Hamer, J., Luxton-Reilly, A., and Purchase, H. 2008. PeerWise: Students Sharing Their Multiple Choice Questions. In Proceedings of the Fourth International Workshop on Computing Education Research. ICER ’08. Association for Computing Machinery, New York, NY, USA, 51–58. event-place: Sydney, Australia.
- Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. 2018. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
- Elo, A. E. 1978. The rating of chessplayers, past and present. Arco Pub.
- Falk, N. and Lapesa, G. 2023. Bridging argument quality and deliberative quality annotations with adapters. In Findings of the Association for Computational Linguistics: EACL 2023, A. Vlachos and I. Augenstein, Eds. Association for Computational Linguistics, Dubrovnik, Croatia, 2424–2443.
- Fisher, A., Rudin, C., and Dominici, F. 2019. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. Journal of Machine Learning Research 20, 177, 1–81.
- Fromm, M., Berrendorf, M., Faerman, E., and Seidl, T. 2023. Cross-domain argument quality estimation. In Findings of the Association for Computational Linguistics: ACL 2023, A. Rogers, J. Boyd-Graber, and N. Okazaki, Eds. Association for Computational Linguistics, Toronto, Canada, 13435–13448.
- Gagnon, V., Labrie, A., Desmarais, M., and Bhatnagar, S. 2019. Filtering non-relevant short answers in peer learning applications. In 11th Conference on Educational Data Mining (EDM2019), C. F. Lynch, A. Merceron, M. Desmarais, and R. Nkambou, Eds. International Educational Data Mining Society, Montreal, Canada, 245–252.
- Garcia-Mila, M., Gilabert, S., Erduran, S., and Felton, M. 2013. The effect of argumentative task goal on the quality of argumentative discourse. Science Education 97, 4, 497–523.
- Ghosh, D., Khanam, A., Han, Y., and Muresan, S. 2016. Coarse-grained argumentation features for scoring persuasive essays. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), K. Erk and N. A. Smith, Eds. Association for Computational Linguistics, Berlin, Germany, 549–554.
- Gleize, M., Shnarch, E., Choshen, L., Dankin, L., Moshkowich, G., Aharonov, R., and Slonim, N. 2019. Are you convinced? choosing the more convincing evidence with a Siamese network. arXiv preprint arXiv:1907.08971.
- Gomis, R. and Silvestre, F. 2021. Plateforme elaastic. https://sia.univ-toulouse.fr/initiatives-pedagogiques/plateforme-elaastic.
- Graesser, A. C., McNamara, D. S., Louwerse, M. M., and Cai, Z. 2004. Coh-Metrix: Analysis of text on cohesion and language. Behavior research methods, instruments, & computers 36, 2, 193–202.
- Gretz, S., Friedman, R., Cohen-Karlik, E., Toledo, A., Lahav, D., Aharonov, R., and Slonim, N. 2020. A large-scale dataset for argument quality ranking: Construction and analysis. In Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 34. AAAI Press, New York, New York, 7805–7813.
- Habernal, I. and Gurevych, I. 2016. Which argument is more convincing? Analyzing and predicting convincingness of Web arguments using bidirectional LSTM. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), K. Erk and N. A. Smith, Eds. Association for Computational Linguistics, Berlin, Germany, 1589–1599.
- Jones, I. and Wheadon, C. 2015. Peer assessment using comparative and absolute judgement. Studies in Educational Evaluation 47, 93–101.
- Khosravi, H., Kitto, K., and Williams, J. J. 2019. Ripple: A crowdsourced adaptive platform for recommendation of learning activities. arXiv preprint arXiv:1910.05522.
- Klebanov, B. B., Stab, C., Burstein, J., Song, Y., Gyawali, B., and Gurevych, I. 2016. Argumentation: Content, structure, and relationship with essay quality. In Proceedings of the Third Workshop on Argument Mining (ArgMining2016), C. Reed, Ed. Association for Computational Linguistics, Berlin, Germany, 70–75.
- Kolhe, P., Littman, M. L., and Isbell, C. L. 2016. Peer Reviewing Short Answers using Comparative Judgement. In Proceedings of the Third (2016) ACM Conference on Learning@ Scale. Association for Computing Machinery, Edinburgh, Scotland, 241–244.
- Le, Q. and Mikolov, T. 2014. Distributed representations of sentences and documents. In International conference on machine learning, E. P. Xing and T. Jebara, Eds. Proceedings of Machine Learning Research, PMLR, Beijing, China, 1188–1196.
- Magooda, A. E., Zahran, M., Rashwan, M., Raafat, H., and Fayek, M. 2016. Vector based techniques for short answer grading. In Proceedings of the twenty-ninth international FLAIRS conference, Z. Markov and I. Russell, Eds. AAAI Press, Key Largo, Florida, 238–243.
- Melnikov, V., Gupta, P., Frick, B., Kaimann, D., and Hüllermeier, E. 2016. Pairwise versus pointwise ranking: A case study. Schedae Informaticae 25, 73–83.
- Mercier, H. and Sperber, D. 2011. Why do humans reason? arguments for an argumentative theory. Behavioral and brain sciences 34, 2, 57–74.
- Mohler, M., Bunescu, R., and Mihalcea, R. 2011. Learning to grade short answer questions using semantic similarity measures and dependency graph alignments. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, D. Lin, Y. Matsumoto, and R. Mihalcea, Eds. Association for Computational Linguistics, Portland, Oregon, 752–762.
- Mohler, M. and Mihalcea, R. 2009. Text-to-text Semantic Similarity for Automatic Short Answer Grading. In Proceedings of the 12th Conference of the European Chapter of the Association for Computational Linguistics, A. Lascarides, C. Gardent, and J. Nivre, Eds. EACL ’09. Association for Computational Linguistics, Stroudsburg, PA, USA, 567–575.
- Nathan, M. J., Koedinger, K. R., Alibali, M. W., and others. 2001. Expert blind spot: When content knowledge eclipses pedagogical content knowledge. In Proceedings of the third international conference on cognitive science, L. Chen, K. Cheng, C.-Y. Chiu, S.-W. Cho, S. He, Y. Jang, J. Katanuma, C. Lee, G. Legendre, C. Ling, M. Lungarella, M. Nathan, R. Pfeifer, J. Zhang, J. Zhang, S. Zhang, and Y. Zhuo, Eds. Vol. 644648. USTC Press, Beijing, China.
- Nguyen, H. V. and Litman, D. J. 2018. Argument Mining for Improving the Automated Scoring of Persuasive Essays. In Proceedings of the AAAI Conference on Artificial Intelligence. AAAI Press, New Orleans, Louisiana, 5892–5899.
- Pelánek, R. 2016. Applications of the Elo rating system in adaptive educational systems. Computers & Education 98, 169–179.
- Pennington, J., Socher, R., and Manning, C. D. 2014. Glove: Global Vectors for Word Representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), A. Moschitti, B. Pang, and W. Daelemans, Eds. Vol. 14. Association for Computational Linguistics, Doha, Qatar, 1532–1543.
- Persing, I. and Ng, V. 2015. Modeling argument strength in student essays. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), C. Xong and M. Strube, Eds. Association for Computational Linguistics, Beijing, China, 543–552.
- Persing, I. and Ng, V. 2016. End-to-End Argumentation Mining in Student Essays. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, K. Knight, A. Nenkova, and O. Rambow, Eds. Association for Computational Linguistics, San Diego, California, 1384–1394.
- Potash, P., Ferguson, A., and Hazen, T. J. 2019. Ranking passages for argument convincingness. In Proceedings of the 6th Workshop on Argument Mining, B. Stein and H. Wachsmuth, Eds. Association for Computational Linguistics, Florence, Italy, 146–155.
- Potter, T., Englund, L., Charbonneau, J., MacLean, M. T., Newell, J., Roll, I., and others. 2017. ComPAIR: A new online tool using adaptive comparative judgement to support learning with peer feedback. Teaching & Learning Inquiry 5, 2, 89–113.
- Raman, K. and Joachims, T. 2014. Methods for ordinal peer grading. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery, New York, New York, 1037–1046.
- Riordan, B., Horbach, A., Cahill, A., Zesch, T., and Lee, C. 2017. Investigating neural architectures for short answer scoring. In Proceedings of the 12th Workshop on Innovative Use of NLP for Building Educational Applications, J. Tetreault, J. Burstein, C. Leacock, and H. Yannakoudakis, Eds. Association for Computational Linguistics, Copenhagen, Denmark, 159–168.
- Silvestre, F., Vidal, P., and Broisin, J. 2015. Reflexive learning, socio-cognitive conflict and peer-assessment to improve the quality of feedbacks in online tests. In Design for Teaching and Learning in a Networked World: 10th European Conference on Technology Enhanced Learning, EC-TEL 2015, Proceedings 10. Springer, Toledo, Spain, 339–351.
- Singh, A., Brooks, C., and Doroudi, S. 2022. Learnersourcing in theory and practice: synthesizing the literature and charting the future. In Proceedings of the Ninth ACM Conference On Learning@ Scale. Association for Computing Machinery, New York, New York, 234–245.
- Stegmann, K., Wecker, C., Weinberger, A., and Fischer, F. 2012. Collaborative argumentation and cognitive elaboration in a computer-supported collaborative learning environment. Instructional Science 40, 2 (Mar.), 297–323.
- Sultan, M. A., Salazar, C., and Sumner, T. 2016. Fast and easy short answer grading with high accuracy. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, K. Knight, A. Nenkova, and O. Rambow, Eds. Association for Computational Linguistics, San Diego, California, 1070–1075.
- Thorburn, L. and Kruger, A. 2022. Optimizing language models for argumentative reasoning. In Proceedings of the 1st Workshop on Argumentation & Machine Learning co-located with 9th International Conference on Computational Models of Argument (COMMA 2022), F. Toni, R. Booth, and S. Polberg, Eds. IOS Press, Cardiff, Wales, 27–44.
- Toledo, A., Gretz, S., Cohen-Karlik, E., Friedman, R., Venezian, E., Lahav, D., Jacovi, M., Aharonov, R., and Slonim, N. 2019. Automatic Argument Quality Assessment-New Datasets and Methods. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), K. Inui, J. Jiang, V. Ng, and X. Wan, Eds. Association for Computational Linguistics, Hong Kong, China, 5629–5639.
- University of British Columbia, T. . L. T. 2019. UBC peer instruction tool for edX. https://github.com/ubc/ubcpi. original-date: 2015-02-17T21:37:02Z.
- Venville, G. J. and Dawson, V. M. 2010. The impact of a classroom intervention on grade 10 students’ argumentation skills, informal reasoning, and conceptual understanding of science. Journal of Research in Science Teaching 47, 8, 952–977.
- Wachsmuth, H., Naderi, N., Hou, Y., Bilu, Y., Prabhakaran, V., Thijm, T. A., Hirst, G., and Stein, B. 2017. Computational argumentation quality assessment in natural language. In Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 1, Long Papers, M. Lapata, P. Blunsom, and A. Koller, Eds. Association for Computational Linguistics, Valencia, Spain, 176–187.
- Weir, S., Kim, J., Gajos, K. Z., and Miller, R. C. 2015. Learnersourcing subgoal labels for how-to videos. In Proceedings of the 18th ACM Conference on Computer Supported Cooperative Work & Social Computing. Association for Computing Machinery, New York, New York, 405–416.
- Williams, J. J., Kim, J., Rafferty, A., Maldonado, S., Gajos, K. Z., Lasecki, W. S., and Heffernan, N. 2016. AXIS: Generating Explanations at Scale with Learnersourcing and Machine Learning. In Proceedings of the Third (2016) ACM Conference on Learning @ Scale - L@S ’16. ACM Press, Edinburgh, Scotland, UK, 379–388.
Appendix A, Argument texts examples
| a1 | a2 |
|---|---|
| I take the view that, school uniform is very comfortable. Because there is the gap between the rich and poor, school uniform is efficient in many ways. If they wore to plain clothes every day, they concerned about clothes by brand and quantity of clothes. Every teenager is sensible so the poor students can feel inferior. Although school uniform is very expensive , it is cheap better than plain clothes. Also they feel sense of kinship and sense of belonging. In my case, school uniform is convenient. I don’t have to worry about my clothes during my student days. | I think it is bad to wear school uniform because it makes you look unatrel and you cannot express yourself enough so band school uniform OK |
| a1 | a2 |
|---|---|
| if a company is not willing to openly say what they are going to do with my data, they shouldn’t be allowed to do it. | if you are against information privacy laws, then you should not object to having a publicly accessible microphone in your home that others can use to listen to your private conversations. |
| a1 | a2 |
|---|---|
| At B, the electric field vectors cancel (E=0). C is further away than A and is therefore weaker. | A is closest, B experiences the least since it is directly in the middle, and C the least since it is most far away. |
| a1 | a2 |
|---|---|
| Law should always to make for the good of their people.If wearing helmet help,then it should be enforce.Also,you cannot assure that every motorcycle in the country would want to pay. | I believe that motorcycle helmets should be mandatory for ALL motorcycle drivers . Although they may be willing to pay their own medical bills , you ca n’t pay anything if you ’re not alive to do so . Motorcycle wrecks can kill the driver , leaving the drivers family with funeral expenses and the like . The family may not be able to afford it . Wearing a helmet increases possibility of surviving a crash that you may not otherwise survive . So yes , motorcycle helmets should be mandatory even if the rider is willing to pay their own medical expenses .. |
1https://github.com/SALTISES4/dalite-ng
2All code for this project available on Github (https://github.com/sameerbhatnagar/convincingness).
3Implementation using python library choix.
4Implementation from Gavel platform.
5POS tagging done using pre-trained models provided with the python package, spacy, which uses the tag set defined by the Universal Dependencies project
7model implementations from Gensim
8Python package PySpellChecker, which uses Levenshtein distance to determine if any given word is too far from known vocabulary
9Spearman correlation was also tested but it is not reported as it yields more or less equivalent results.
10Implementation from SciKit-Learn